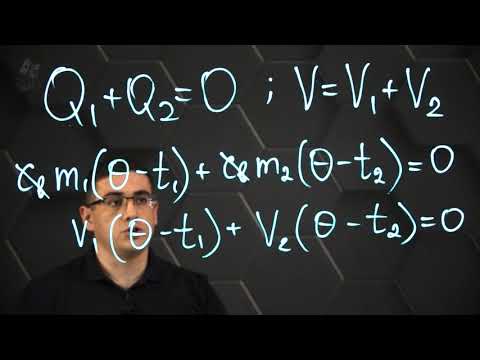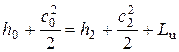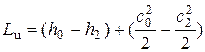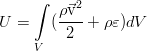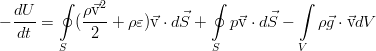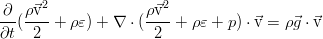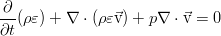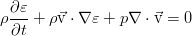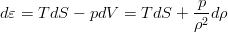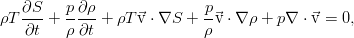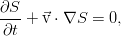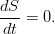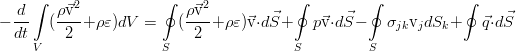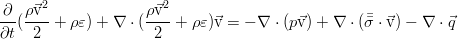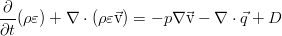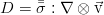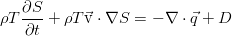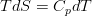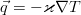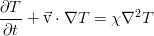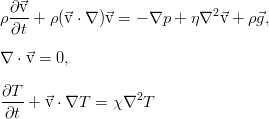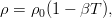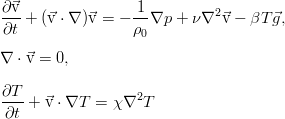Уравнение сохранения энергии для потока (7 видео)

Содержание

Тема № 4: Основные уравнения газового потока в лопаточных машинах
Кратко о гидродинамике: сохранение энергии
Перенос энергии в идеальной жидкости
Учёт вязкости. Уравнение теплопроводности
Конвекция. Приближение Буссинеска
Проблема инструментария
Далее
Закон Бернулли как следствие закона сохранения энергии
🌟 Видео

Видео:Галилео. Эксперимент. Закон сохранения энергииСкачать

Тема № 4: Основные уравнения газового потока в лопаточных машинах

Преобразование энергии расширения рабочего тела в энергию вращения ротора происходит в результате обтекания потоком неподвижных сопловых и рабочих решеток.

Законы течения сжимаемой жидкости имеют большое значение для изучения процессов, происходящих в ступени.

Теория лопаточных машин базируется на основных уравнениях движения газа: уравнении неразрывности, уравнении сохранения энергии, уравнении первого закона термодинамики, уравнении Бернулли и уравнениях Эйлера. Эти уравнения рассматриваются в курсе термодинамики. Здесь остановимся лишь на некоторых особенностях этих уравнений, которые связаны с их использованием в расчетах лопаточных машин. Уравнение Эйлера о количестве движения применительно к ступени турбины будет рассмотрено ниже.

Реальное течение рабочего тела в ступени турбомашины является пространственным периодически неустановившимся течением вязкого сжимаемого газа, математическое исследование которого в строгой постановке затруднительно. Для получения относительно простых уравнений, которые можно без труда использовать в инженерных расчетах, делаются некоторые упрощения:

1) рассматривают осредненные значения параметров в точке (стационарность);

2) во всех сечениях каждой ступени неизменными.

Указанные допущения означают, что число лопаток СА и РК бесконечно.

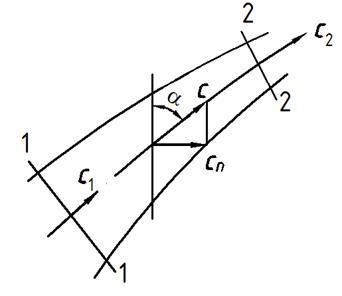
Уравнение неразрывности в случае установившегося течения формулируется следующим образом: секундный массовый расход газа через любое поперечное сечение элементарной струйки при установившемся течении сохраняется постоянным (см. рис. 4.1).

Рис. 4.1. К выводу уравнения неразрывности

Если в рассматриваемых сечениях элемента двигателя поток является равномерным или рассматриваются осредненные параметры газового потока в этих сечениях, то уравнение неразрывности с равным основанием может быть записано и для всего потока. В частности, для сечений, нормальных к оси потока:

. (2.1)

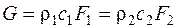
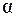
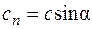
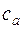
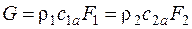
В общем случае, когда выбранное сечение не перпендикулярно к оси струйки, а составляет с ней некий угол , нужно рассматривать нормальную составляющую скорости в этом сечении (т. е. в применении к теории ступени турбомашин – осевую составляющую скорости ), а уравнение неразрывности записывается в виде:

. (2.2)

Уравнение первого закона термодинамики

Уравнением первого закона термодинамики пользуются для определения параметров состояния газа при осуществлении термодинамического процесса. Оно является частным выражением закона сохранения энергии для элементарного объема газа, написанным в системе координат, движущейся вместе с рассматриваемым элементом объема или, в частном случае, для покоящегося газа.

Для элементарного объема газа уравнение первого закона термодинамики имеет вид:

, (2.7)

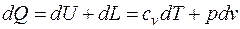
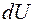
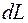
т. е. все тепло, подведенное к рассматриваемому объему газа, идет на изменение внутренней энергии и на совершение работы против сил давления, связанной с изменением объема.

Для движущегося газа удобно вместо внутренней энергии пользоваться понятием энтальпии:

. (1.8)

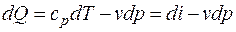
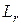
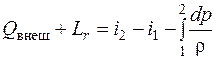
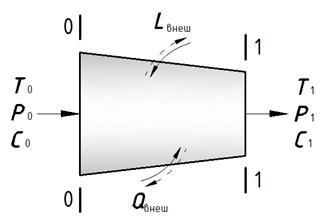
Переходя к интегральной форме записи, с учетом того, что тепло трения эквивалентно работе сил трения , можно получить:

, (1.9)

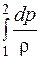
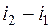
т. е. все тепло, подводимое к потоку между сечениями 1–1 и 2–2 (рис. 2.2), состоящее из тепла, подводимого извне, и тепла, выделяющегося в результате трения (работы сил трения), идет на совершение работы сжатия (расширения) и на изменение внутренней энергии потока ( ).

Уравнение первого закона термодинамики удобно для определения работы сил трения по известному значению показателя политропы 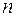, который легко определяется по термодинамическим соотношениям, если известны параметры потока в начале и в конце процесса.

Обобщенное уравнение Бернулли

Основным уравнением, на котором строятся расчеты турбомашин, является уравнение Бернулли:

. (2.10)

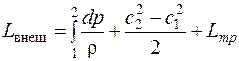
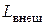
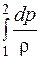
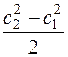
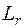
Уравнение (2.10) можно трактовать так: подведенная извне энергия идет на работу сжатия (расширения) газа , приращение кинетической энергии и преодоление гидравлического сопротивления .

Заметим, что уравнение Бернулли не зависит от теплообмена с окружающей средой. Однако теплообмен оказывает косвенное влияние на показатель политропы процесса.

Уравнение Бернулли, как и уравнение сохранения энергии, можно отнести к энергетическим и получить его из рассмотрения баланса механической энергии.

При свободном движении идеального газа, при отсутствии энергии, подведенной извне и потерь на преодоление гидравлического сопротивления:

. (1.11)

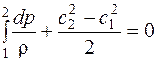
Для идеальной несжимаемой жидкости, для которой :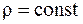

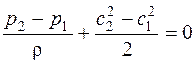
, (1.12)

т. е. для повышения давления в компрессоре динамического действия необходимо затормозить поток.

Самый простой способ достичь этого – геометрическое воздействие:

, (1.13)

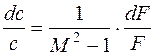
Таким образом, при дозвуковом потоке ( 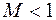) расширение канала приводит к снижению скорости потока. На замедляющийся поток набегают следующие молекулы, что приводит к снижению удельного объема (увеличению плотности), т. е. давление газа растет.

Можно сделать вывод, что рабочий процесс турбокомпрессора состоит из двух взаимосвязанных, одновременно протекающих процессов:

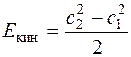
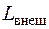
— приращения кинетической энергии за счет подводимой внешней работы (от турбины) ;

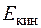
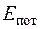
— преобразования кинетической энергии потока в энергию потенциальную , пропорциональную давлению.

Уравнение сохранения энергии

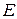
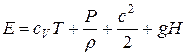
Полная энергия рабочего тела может быть записана в виде:

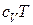
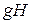
где — внутренняя энергия; P/r – потенциальная энергия давления; С 2 /2 – кинетическая энергия; — потенциальная энергия положения.

Данное выражение можно упростить.

Потенциальной энергией положения 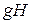можно пренебречь, т.к. по сравнению с остальными слагаемыми она ничтожна.

Внутренняя энергия рабочего тела в сумме с потенциальной энергией давления P/r будут равны энтальпии рабочего тела h, которая, таким образом, является мерой той потенциальной энергии, которой обладает поток рабочего тела.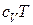

В этом случае уравнение полной энергии запишется в виде:

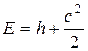
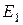
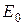
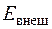
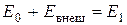
Уравнение сохранения энергии может быть сформулировано следующим образом: полная энергия газового потока на выходе из рассматриваемого элемента (рис. 4.2) больше (или меньше) полной его энергии на входе на величину энергии, подведенной (или отведенной) между рассматриваемыми сечениями :

Рис. 4.2. К выводу уравнения сохранения энергии

Поскольку при установившемся движении газа расходы через сечения 0–0 и 1–1 одинаковы, то все члены уравнения сохранения энергии принято представлять отнесенными к 1 кг газа.

Применительно к турбомашинам уравнение сохранения энергии можно записать в виде:

, (2.3)

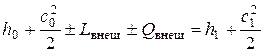
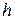
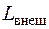
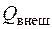
где – энтальпия газа (отвечает за внутреннюю и потенциальную энергию потока), с 2 /2 – кинетическая энергия потока; и – внешняя подведенная (отведенная) энергия, в виде механической работы и в виде тепла соответственно.

Для элементов двигателя, в которых отсутствует подвод или отвод энергии, уравнение сохранения энергии в частном случае имеет вид:

, (2.4)

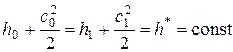
т. е. при отсутствии энергообмена полная энергия газового потока сохраняется неизменной и равна энтальпии заторможенного потока.

Запишем уравнение сохранения энергии для турбинной ступени (см. рис. 2.1). Теплообменом с окружающей средой при этом можно пренебречь, т.к. при относительно небольших площадях теплоотдачи и хорошей теплоизоляции коэффициенты теплоотдачи малы.

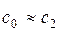
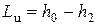
Обычно для турбинной ступени , поэтому

т.е. работа турбинной ступени фактически численно равна изменению энтальпии потока.

Заметим, что в различные записи уравнения сохранения энергии в явном виде не входит трение, а значит, это уравнение применимо как для идеального газа, так и газа, обладающего вязкостью.

Силы трения, которые возникают на стенках, ограничивающих поток газа, и силы внутреннего трения между отдельными струйками газа являются внутренними силами, а работа на их преодоление переходит практически полностью в тепло. Трение приводит лишь к преобразованию одного вида энергии в другой и не отражается на общем балансе энергии. Например, если вследствие трения уменьшается кинетическая энергия, то энтальпия в этом сечении вырастет на ту же величину.

Дата добавления: 2015-06-17 ; просмотров: 3793 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Алгоритм решения задач на Закон сохранения энергииСкачать

Кратко о гидродинамике: сохранение энергии

В очередной раз извиняюсь за медленное написание постов в запланированной серии. В этот раз причина промедления объективна, в виде конференции в Вене, хотя и имеет значимую субъективную составляющую в виде собственного там участия и некоторых бюрократических моментов подготовки и оплаты.

Данный пост рассматривает законы сохранения энергии в идеальной и вязкой жидкости. Они заведомо необходимы для полноты описания движения, однако, в изотермическом случае теплообмена как такового нет, и потому для описания достаточно использовать уравнение Навье-Стокса и уравнение неразрывности. Надеюсь, этот пост будет последним из достаточно абстрактных постов, описывающих общую теорию и не практически привязанных к конкретным постановкам задач.

Постараюсь уменьшить количество выкладок, ибо они, конечно, важны, но результаты в виде конечных уравнений — важнее.

Перенос энергии в идеальной жидкости

Итак, сохранение энергии. Подход к описанию абсолютно стандартный — мы вводим некоторую величину, находим, какие механизмы отвечают за её изменение и пишем закон сохранения сперва в интегральной форме, а затем, сведя все поверхностные интегралы к объёмным по теореме Гаусса — в дифференциальной.

Энергия жидкости в классической гидродинамике, не учитывающей также такой эффект, как электропроводность и соответствующее взаимодействие с внешними и внутренними электромагнитными полями, складывается из внутренней и кинетической энергии. Она равна такому интегралу:

Изменяться в пределах нашего объёма V энергия может за счёт простого её перетекания вместе с потоком жидкости, работы сил давления от внешних элементов жидкости и работы внешних сил (ниже показаны на примере силы тяжести):

В идеальной жидкости нет трения, и потому нет рассеяния энергии за счёт вязкости. Кроме того, здесь пренебрегается и процессами теплопроводности, что так же присуще идеальной жидкости как отсутствие ещё одного механизма диссипации энергии. В дифференциальной форме закон сохранения полной энергии выглядит так:

Однако, его можно благополучно упростить. Воспользовавшись уравнением Эйлера (см. предыдущий пост), скалярно домноженным на скорость, можно выделить из полученного закона сохранения такую часть:

А это уже преобразуется к ещё более простому виду:

Тут уже можно вспомнить термодинамику. Первое начало термодинамики (с пометкой — для удельного объёма жидкости, т.е. объёма, масса которого равна единице):

позволяет вполне очевидным образом связать производные энергии, энтропии и плотности (как обратной объему величины). Используя эту связь дифференциалов величин в уравнении для энергии:

а также закон сохранения массы, получим ещё одно уравнение, которое описывает эволюцию энтропии в жидкости:

В движущейся системе отсчёта, привязанной к тому элементу жидкости, для которого это всё написано, уравнение упрощается ещё сильнее:

То есть, энтропия отдельной произвольной жидкой частицы (в идеальной жидкости) сохраняется. Энтропия просто пассивно переносится потоком, попутно связывая уравнением состояния давление и плотность среды.

Учёт вязкости. Уравнение теплопроводности

Теперь учтём вязкую и теплопроводную диссипацию. В интегральном виде они представляется парой добавочных слагаемых в законе сохранения:

Они описывают работу сил вязкого трения на границе элемента жидкости и тепловой поток через границу. В дифференциальной форме уравнение сохранения полной энергии:

Произведя ряд операций над этим соотношением с применением уравнения переноса импульса в общем виде (для произвольного тензора вязких напряжений) и уравнения неразрывности (а именно — домножив закон сохранения массы на половину квадрата скорости, закон сохранения импульса — на скорость, сложив их между собой и вычтя итог из уравнения для полной энергии), мы избавимся от слагаемых с кинетической энергией:

Здесь возникает диссипативная функция, равная двойной свёртке тензора вязких напряжений и тензора, который условно иногда называют градиентом скорости:

Применив здесь уравнение баланса массы и первое начало термодинамики аналогично тому, как это сделано выше, приходим к уравнению баланса энтропии:

Видно, что оно отличается от уравнения в идеальной жидкости только ненулевой правой частью. Для несжимаемой жидкости мы можем благополучно перейти от энтропии к более осязаемой величине, то бишь — к температуре, используя определение теплоёмкости при постоянном давлении:

Наконец, можно пренебречь диссипативной функцией, т.к. она описывает выделение за счёт внутреннего трения, и потому существенна только в жидкостях с очень большими вязкостями, а для потока тепла воспользоваться законом теплопроводности Фурье, позволяющим выразить его через температуру:

В итоге получается уравнение теплопроводности несжимаемой вязкой жидкости:

Согласно ему, температура элемента жидкости изменяется за счёт непосредственного конвективного переноса с потоком жидкости, а также за счёт вполне обычного механизма молекулярной теплопроводности (правая часть).

Конвекция. Приближение Буссинеска

Собственно, с описания задачи конвекции на хабре и начался весь этот гидродинамический «балаганчик». Итак, мы смотрим на баночку с несжимаемой вязкой жидкостью, например, водой. Движение её в случае неоднородной температуры в объёме описывается тремя уравнениями:

В общем случае в эту систему входит ещё уравнение состояния, связывающее плотность, давление и температуру. Однако тогда жидкость уже нельзя считать несжимаемой. Практика же (да и математика) показывает, что с достаточной точностью можно принять плотность постоянной везде, кроме слагаемого с силой тяжести. Более того, достаточно ограничиться линейным разложением по температуре:

Сразу отметим, что здесь записана уже не абсолютная температура, а уже отклонение от некоторого «нулевого» уровня, при котором плотность равна 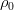. Писать так нам позволяет уравнение теплопроводности, благо оно линейное и к таким сдвигам инвариантно. Можно выделить в слагаемом при силе тяжести независимую от температуры часть (гидростатический градиент) и спрятать её в давление:

И тогда мы приходим к уравнениям конвекции в приближении Буссинеска:

Данная модель практически общеупотребительна при изучении конвективных явлений, и на её основе было получено огромное количество самых разных по значимости результатов. В частности, в задачах устойчивости равновесия жидкости и прочих.

Проблема инструментария

Немного отступлю от темы, хотя прекрасно понимаю, что это может только разжечь лишнюю и отвлекающую дискуссию.

Знаете, что удивило в комментариях по предыдущему посту? То, что читатели уделяют много внимания вопросу математической строгости выкладок, которой тут, в общем-то, немного. Гидродинамика создана Эйлером и Навье во времена господства французского материализма, когда строгие результаты аналитической механики описали, казалось, весь мир. Но уровень строгости этих результатов таков, каким он мог быть в те времена, в едва только-только созданном Ньютоном и другими дифференциальном исчислении, и не выше. И таким он остался по сей день, и такой же является математическая строгость гидродинамики. Практически, это последняя классическая область науки, которая ещё имеет нерешённые фундаментальные проблемы. Может быть, не решены они именно потому, что сформулированы на том, старом, не сильно развитом и не богатом значительными средствами языке. Помнится, есть отдельные наработки в математике, где к уравнениям Навье-Стокса применяют аппарат, не к ночи будь помянут, биспиноров и гамма-матриц Дирака (основу квантовой теории поля) или ещё чего похуже. Но они до сих пор отдельные и практически неизвестные.

Лично я предполагаю, что развитие аппарата для решения уравнений Навье-Стокса ещё попросту не состоялось. Ведь, как известно, эти уравнения отлично описывают и упорядоченные ламинарные течения, и хаос турбулентности. А в уравнениях для этого всего-то достаточно изменить один управляющий параметр. Как в нелинейных системах (а-ля система Лоренца), которые тоже не имеют общих аналитических решений, да и, в целом, конкретного детального анализа свойств решений именно как математических функций. Многое на уровне поведения — тут хаос, там упорядочение, там синхронизация, здесь влияние параметра, а переход, по-видимому, происходит вот таким образом. Но ни о гладкости решений, ни об их существовании вопроса в таких задачах нет, в отличие от Навье-Стокса. Ведь мы же до сих пор практически не знаем — существуют ли вообще их общие гладкие решения.

Увидев в комментариях вещи навроде «набла — это 1-форма», сперва сильно задумался, не упустил ли чего в своём образовании. Да, про разного рода n-формы у меня в курсах упоминалось (но не более) в одном семестровом спецкурсе под названием теории групп в физике, из которого, правда, много вынести не удалось ввиду отсутствия серьёзной структурированности изложения. Но рассуждать о том, набла — вектор или же нет, никогда не приходится. В физике, не касающейся значительно математизированных проблем уровня, скажем, общей теории относительности и неотъемлемо нужной для неё дифференциальной геометрии, набла всегда была практически вектором. Конечно, не совсем обычным, не коммутирующим с ними и обладающим рядом иных свойств. Простой, в общем-то даже обычный оператор, который показывает, какую компоненту вектора и каким образом мы будем дифференцировать. Просто инструмент, которым мы умеем пользоваться в заданных пределах и осознаём, что нужно проверить его пригодность при выходе за границу привычной области, даже, например, при переходе от декартовых координат к тем же сферическим.

Иногда можно потратить излишне много времени на понимание устройства молотка, но так толком и не научиться забивать им гвозди. Например, почему он имеет такую форму, почему разные молоты имеют разную форму, а затем начать копать глубже — почему блестит металл, а деревянная ручка — нет, и др. Но от этого понимания сущность наиболее частого применения молотка не поменяется. Им будут забивать гвозди, выравнивать металл по оправке и т.д. — им всё равно будут стучать, желательно, не по пальцам.

На таком уровне находится моё личное знакомство с аппаратом квантовой электродинамики. По принципу — помню, что-то проходил. Более того, даже методичку в прошлом году издали с преподавателем этого предмета, но как-то оно всё равно в стороне — не занимаюсь этим.

Следующий пост будет посвящён проблемам устойчивости для равновесия и стационарного течения. Там в очередной раз мы увидим, что даже простейшие задачи гидродинамики не могут быть решены аналитически в полном виде, и потому приходится применять множество различных, на первый взгляд весьма спорных, но в то же время прекрасно работающих и обоснованных методик. Надеюсь, что уже удастся перейти от абстрактности к более осязаемым вещам.

Видео:Закон сохранения энергии. 9 класс. Решение задачСкачать

Закон Бернулли как следствие закона сохранения энергии

Разделы: Физика

Цели урока:

Изучить частный случай закона сохранения энергии в применении к объяснению зависимости давления от скорости движения жидкости и газа;
Сформулировать закон Бернулли;
Рассмотреть примеры его применения и проявления на практике.

Тип урока: комбинированный.

Оборудование: компьютер, мультимедийный проектор, экран, презентация к уроку.

Оборудование для демонстраций: весы, макет крыла самолета, небольшая воронка, теннисный шарик, воздуходувка (фен), демонстрационный манометр, таблички на магнитах с физическими формулами.

Оборудование для практических работ: стакан с водой, одноразовый шприц, два листа бумаги, бруски.

I. Организационный момент.

Тема, скорее название, нашего урока звучит не совсем обычно. Может быть кто-то из вас подумал: причем здесь физика? А действительно, причем здесь физика? А это и предстоит нам выяснить сегодня. В конце урока вы должны будете сами сформулировать правильно “физическую” тему. Я же скажу только, что эти объекты объединены одним и тем же законом, а именно, законом сохранения полной механической энергии. Работать вы будете на рабочих картах (приложение 1). Напишите свою фамилию на карте в правом верхнем углу.

II. Актуализация знаний.

Итак, начинаем. Раз уж я упомянула закон сохранения механической энергии, то давайте его вспомним.

1. Что утверждает закон сохранения полной механической энергии?
2. Что называется полной механической энергией?
3. Какая энергия называется кинетической? По какой формуле рассчитывается?
4. Какая энергия называется потенциальной? Формулы потенциальной энергии.

III. Основная часть. Изучение нового материала.

Сегодня на уроке мы будем говорить о применении закона сохранения для движущихся потоков жидкостей и газов. Движение жидкостей и газов разделяется на ламинарное и турбулентное. На дидактических картах (приложение 2) у вас есть их определения. Давайте прочитаем. Мы будем рассматривать ламинарное течение.

А начнем мы с вопроса: можно ли удержать шарик в вертикальной воронке, выдувая из нее воздух? Хорошо, давайте проверим это на опыте. Критерием любой истины является опыт. Мне нужен помощник, который выполнит этот несложный эксперимент. Оказывается, чтобы удержать шарик в воронке надо выдувать воздух. Кто же может объяснить этот “парадокс”? Тогда запишем первый вопрос в таблицу на рабочей карте. Почему при выдувании воздуха из воронки шарик удерживается в ней?

Продолжаем отвечать на вопросы. Что произойдет с листом бумаги, если подуть над ним? Расположите лист бумаги на уровне рта и с силой продуйте воздух. Что произошло с листом бумаги? А почему? Запишите в таблицу на рабочих картах и этот вопрос: почему поднялся листок?

Проведем еще один опыт. Наберите в шприц воды из стакана и, надавливая на поршень, выпустите ее (добейтесь, чтобы она вытекала непрерывной струёй). Сначала выполняет товарищ по парте, а сосед наблюдает. Потом поменяйтесь ролями. Обратите внимание на толщину вытекающей струи. Струя становится уже. А теперь надо объяснить увиденное. Есть какие-то предположения? Записываем в таблицу второй вопрос: почему струя вытекающей воды становится уже? К этим вопросам мы вернемся попозже.

Что ж, вопросов, наверно, пока достаточно. Пора искать ответы. Поможет в этом известный вам закон сохранения механической энергии и неизвестный пока закон Бернулли.

Рассмотрим ламинарное течение жидкости по трубе разного сечения. Посмотрите на слайд. Там, где сечение не меняется скорость тоже остается постоянной. Но одинакова ли скорость течения жидкости на различных участках? И где больше? А может кто-нибудь объяснить почему? (Так как жидкость несжимаема, то за одинаковый промежуток времени t через каждое из этих сечений должна пройти жидкость одного и того же объема. Но как жидкость, протекающая через первое сечение может “успеть” за то же время протечь через значительно меньшее сечение ? Очевидно, что для этого при прохождении узких частей трубы скорость движения жидкости должна быть больше, чем при прохождении широких).

Покажите на рисунке 1 в рабочих картах векторы скоростей в различных участках. А теперь проверим как это получилось у меня (слайд). Значит, скорость зависит от сечения. Более того, зависимость эта обратно пропорциональна. Математически это выражается следующим соотношением, которое носит название уравнения неразрывности струи: VS= const, здесь – V скорость жидкости, S – площадь сечения трубы, по которой течет жидкость. Сформулировать этот закон можно так: сколько вливается жидкости в трубу, столько должно и выливаться, если условия течения не изменяются. Скорость в узких участках трубы должна быть выше, чем в широких.

Отсюда следует, что

Вывод: чем меньше площадь сечения, тем больше скорость.

Задача №1. Как и во сколько раз изменится кинетическая энергии жидкости, если сечение трубы уменьшить в 2 раза? (Ответ увеличится в 4 раза). А потенциальная энергия? Осторожно, ошибка!

Потенциальная энергия уменьшится, но необязательно в 4 раза!

(Например: 100 = 100, 100 = 10 + 90, 100 = 40 + 60)

С вопросом о скорости вы справились хорошо. А что скажете о давлении воды в разных частях? Если изменяется, то как? На рисунке 2 отметьте уровень воды в вертикальных трубках в зависимости от давления жидкости в горизонтальной трубе. А теперь посмотрим, на этот слайд . В узких местах трубы высота столбика жидкости меньше, чем в широких. О чем говорит разная высота воды? Оказывается, в узких местах трубы давление жидкости меньше, чем в широких. А почему?

При переходе жидкости из широкого участка в узкий скорость течения увеличивается, то это значит, что где-то на границе между узким и широким участком трубы жидкость получает ускорение. А по второму закону Ньютона для этого на этой границе должна действовать сила. Этой силой может быть только разность между силами давления в широком и узком участках трубы. В широком участке трубы давление должно быть больше, чем в узком. Этот вывод следует из закона сохранения энергии. Если в узких местах трубы увеличивается скорость жидкости, то увеличивается и ее кинетическая энергия. А так как мы условились, что жидкость течет без трения, то этот прирост кинетической энергии должен компенсироваться уменьшением потенциальной энергии, потому что полная энергия должна оставаться постоянной. Но это не потенциальная энергия “mgh”, потому что труба горизонтальная и высота h везде одинакова. Значит, остается только потенциальная энергия, связанная с силой упругости. Сила давления жидкости – это и есть сила упругости сжатой жидкости. В широкой части трубы жидкость несколько сильнее сжата, чем в узкой. Правда, мы только что говорили, что жидкость считается несжимаемой. Но это значит, что жидкость не настолько сжата, чтобы сколько-нибудь заметно изменился ее объем. Очень малое сжатие, вызывающее появление силы упругости, неизбежно. Оно и уменьшается в узких частях трубы.

Чтобы разобраться в причинах уменьшения давления в узких частях и увеличения в широких, используем закон сохранения энергии и математические навыки. Я начну, а вы будете помогать.

Работа сил давления, совершенная над элементом жидкости при его перемещении, равна:

здесь =V₁ и =V ₂ – объемы жидкости, прошедшей за одно и тоже время через сечения 1 и 2. Подставим (2) в (1) и получаем:

Так как высота центра масс трубы не меняется, то h₁ = h _{2 .} Выберем нулевой уровень, проходящий через центр масс, тогда mgh ₁ = mgh₂ = 0.

Так как жидкость практически несжимаема, то объемы ее, прошедшие за одно и тоже время равны, V_{1 =} V ₂ (или ), поэтому обе части равенства можно разделить обе части на V.

(*)

Таким образом, если скорость, например, увеличивается, то увеличивается первое слагаемое, значит, чтобы равенство выполнялось, на такую же величину второе слагаемое уменьшается, т.е. уменьшается давление.

Вывод: Чем больше скорость потока жидкости, тем меньше ее давление.

Зависимость давления от скорости течения называют эффектом, а уравнение (*) – законом Бернулли в честь автора, швейцарского ученого Даниила Бернулли, который, кстати, работал в С.Петербурге. Закон Бернулли для ламинарных потоков жидкости и газов является следствием закона сохранения энергии.

Убедимся на опыте, что полученный вывод справедлив и для газов. Для этого выполним еще практические задания (описание на дидактической карте).

1 Вариант. Возьмите в руки два листка бумаги и расположите их на расстоянии3– 4см друг от друга и продуйте несильно между ними воздух. Что наблюдаем? Почему? Между листочками давление уменьшилось, а снаружи осталось таким же. Повторите опыт, но подуйте теперь сильнее. Объясните этот результат.

2 Вариант. Положите листок на две книги, как показано на слайде. Продуйте воздух под листком сначала несильно, а потом сильнее. Объясните, что вы наблюдали.

Настало время для ответов на оставленные вами, но не забытые мною вопросы:

Почему при выдувании воздуха из воронки шарик удерживается в ней?
Почему поднялся листок?
Почему струя вытекающей воды становится уже?

Запишите ответы в таблицы.

Вот и настала очередь самолетов. Посмотрим видеофрагмент (Приложение 4).

Так почему же поднимается самолет? В чем причина возникновения подъемной силы?

Все дело в форме крыла и в угле атаки.

Убедимся на опыте (рисунок 1). Почему нарушилось равновесие весов?

Кстати сказать, у птиц крыло тоже имеет похожую форму.

Эффект Бернулли — это то, благодаря чему птицы и самолеты могут летать. Разрез крыла у них практически одинаковый: за счет сложной формы крыла создается разница обтекающих его сверху и снизу воздушных потоков, что позволяет телу подниматься вверх.

Формулу для расчета подъемной силы впервые получил наш соотечественник Николай Егорович Жуковский – “отец русской авиации”.

Что касается белок – летяг, то они, конечно же не могут развить большую скорость и форма “крыльев” немножко другая, поэтому и подъемная сила у них невелика и возникает она в большой степени из-за угла наклона. Как и обычная белка, летяга большую часть жизни проводит на деревьях, но на землю спускается гораздо реже. Между передними и задними лапами у неё имеется кожная перепонка, которая позволяет планировать с дерева на дерево. Так белка-летяга преодолевает расстояние до 50–60 м по нисходящей параболической кривой. Для прыжка летяга забирается на верхушку дерева. Во время полёта её передние конечности широко расставлены, а задние прижаты к хвосту, образуя характерный треугольный силуэт. Меняя натяжение перепонки, летяга маневрирует, иногда изменяя направление полёта на 90°. Хвост в основном выполняет роль тормоза. Посадку на ствол дерева летяга обычно совершает по касательной, как бы сбоку. Перед посадкой принимает вертикальное положение и цепляется всеми четырьмя лапами, после чего сразу перебегает на другую сторону ствола. Этот маневр помогает ей уворачиваться от пернатых хищников.

Задача№2: В полете давление воздуха под крылом самолета 97,8 кН/м 2 , а над крылом 96,8 кН/м 2 . Площадь крыла 20 м 2 . Определить подъемную силу.

Решение: F = PS, где P = P₂ – P _1, тогда F = ( P₂ – P ₁)S, F =20 . 10 3 H

Задача №3. О “крученых мячах” вы прочитаете самостоятельно текст и ответьте на вопросы.

Эффект Магнуса.

Почему движущиеся вращающиеся тела отклоняются от прямолинейной траектории?
Почему давление на мяч с разных сторон различно?
Почему относительная скорость воздушного потока различна по разные стороны мяча?

Можно привести еще множество примеров: бумеранг, летающие тарелки, водоструйный насос, распылители, карбюраторы, катера на подводных крыльях.

А вот посмотрите, какую опасность представляет уменьшение давления для морских судов. Поток воды между судами имеет меньшее давление, чем снаружи. Все моряки знают, что два судна, идущих рядом на больших скоростях сильно притягиваются друг к другу. Еще опаснее, когда один корабль идет за другим. Силы притяжения, возникшие из-за разности давлений, стремятся корабли развернуть . Задний корабль разворачивается сильнее переднего. Столкновение в таких случаях неизбежно.

Задача №4. Очень часто лоцманы жалуются на коварные мели, которые так и притягивают к себе суда. Почему мели на реках притягивают суда?

IV. Закрепление изученного материала

1. Жидкость течет через трубу с переменным поперечным сечением. В каком сечении трубы скорость “v” течения жидкости и ее давление “P” на стенках максимальна?

v и P максимальны в сечении 1;
v и P максимальны в сечении 2;
v максимальны в сечении 1, P – в сечении 2;
v максимальны в сечении 2, P – в сечении 1;
v и P одинаковы во всех сечениях.

2. В какой трубке уровень воды будет выше?

3. Что произойдет, если продувать струю воздуха между двумя шариками от пинг-понга, подвешенными на нитях (смотри рисунок)?

Останутся неподвижными;
Будут двигаться вместе вправо или влево;
Отклонятся друг от друга;
Приблизятся друг к другу.

Подводя итог нашего урока, вспомним еще раз основные законы и уравнения, с которыми познакомились на уроке:

Уравнение неразрывности струи – какую зависимость и каких величин оно выражает?
Закон Бернулли – что он утверждает?

V. Рефлексия . Подведение итогов урока.

А теперь настало время дать нашему уроку “физическое” название. Какие будут ваши предложения?

Закон Бернулли как следствие закона сохранения энергии. (Проявление и применение закона сохранения энергии для движущихся потоков жидкости и газов).

VI. Домашнее задание.

Домашнее задание:

Задачи № 404, 406, 409, 410 (Рымкевич А.П. Физика. Задачник. 10-11 классы.- М.: Дрофа, 2003)
Домашняя практическая работа: Сделайте из тонкой бумаги цилиндр диаметром 3 см, длиной 20 см. Положите его на стол на наклонную плоскость. Пронаблюдайте за траекторией, по которой скатывается цилиндр. Объясните наблюдаемое явление.