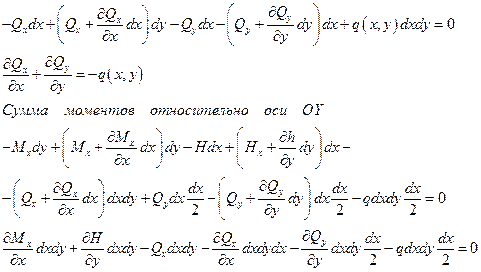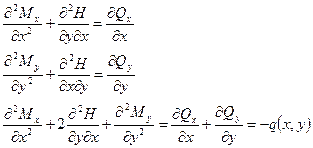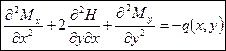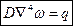Введенные гипотезы позволяют выразить перемещения и и v (рис. 20.3) через прогиб пластины. В соответствии с формулой (20.2) прогиб не зависит от координаты z, то есть w = w(x, у). Подставив в формулы (20.1) соотношения Коши, получим

См., например: Тимошенко С.П., Войновский-Кригер С. Пластинки и оболочки. М.: Физматгиз, 1966.
Проинтегрировав эти равенства по переменной z, находим
где /,(х, у) и f2(x, у) — произвольные функции, появляющиеся при интегрировании дифференциальных уравнений в частных производных. Для определения этих функций используем условия (20.3)
С учетом этих условий формулы для перемещений и и v принимают следующий вид:
Определим линейные и угловую деформации:
Видео:Изгиб тонких пластин (часть 1)Скачать

Напряжения в пластинах при изгибе. Дифференциальное уравнение изгиба пластины
Для определения напряжений в пластинах используем формулы обобщенного закона Гука в обратной форме, в которых положим = 0. При этом с учетом формул (20.5) получим
Как видно из формул (20.6), напряжения о, о и т изменя-
ются по толщине пластины по линейному закону и равны нулю в точках на уровне срединной плоскости. Характер изменения этих напряжений показан на рис. 20.4, а, б.
Касательные напряжения xxz и xyz в соответствии с формулами
- (20.1) должны быть равны нулю. Однако в общем случае нагружения пластины это противоречит уравнению равновесия XZ = 0, так как поперечная нагрузка может оказаться неуравновешенной. Для определения касательных напряжений xxz и xyz можно использовать первое и второе дифференциальные уравнения равновесия
- (16.1) без учета объемных сил. На основании первого уравнения запишем
Подставив в это уравнение выражения (20.6) для напряжений ах и т , получим
Упростив это равенство и произведя его интегрирование по переменной z, находим
где 
/3(х, у) — произвольная функция, для определения которой используем условие отсутствия касательных (сдвигающих) нагрузок на внешних поверхностях пластины:
Использовав эти условия, получим
Аналогичные выкладки можно произвести на основании второго дифференциального уравнения равновесия (16.1). В результате получим следующие формулы:
Касательные напряжения xxz и %zy изменяются по толщине пластины по закону квадратной параболы, так же как касательные напряжения в балках прямоугольного сечения при изгибе. Максимальных значений они достигают в точках срединной плоскости. Эпюры касательных напряжений txz и приведены на рис 20.5.
В соответствии с гипотезой об отсутствии взаимного давления между продольными слоями пластины напряжение а, положено равным нулю, что позволило упростить закон Гука. Однако это противоречит граничным условиям на внешних поверхностях пластины при наличии распределенных поперечных нагрузок. Для определения az используем третье дифференциальное уравнение равновесия (16.1), в котором объемные силы положим равными нулю. На основании этого уравнения запишем
Подставим в это уравнение формулы (20.7) для касательных напряжений и и проинтегрируем его по переменной z’-
Здесь f4(x, у) — произвольная функция.
Считая, что пластина находится под действием распределенной поперечной нагрузки q(x, у), приложенной к верхней поверхности пластины, а нижняя поверхность свободна от нагрузки, поставим следующие граничные условия:
Использовав эти условия, получим
Сложив эти уравнения, находим
С учетом этого выражения формула для напряжения az принимает следующий вид:
Нетрудно видеть, что напряжение а, изменяется по толщине пластины по закону кубической параболы, так же как в балках прямоугольного сечения, находящихся под действием распределенной нагрузки. Характер эпюры а, показан на рис. 20.6.
Расчеты показывают, что в тонких пластинах напряжение о, значительно меньше напряжений ох и о и им вполне обоснованно можно пренебречь.
Вычитая одно из другого уравнения системы (20.8), получим где обозначено
Величина D называется жесткостью пластины при изгибе.
Запишем уравнение (20.10) в следующем виде:
Это дифференциальное уравнение является основным уравнением, описывающим изгиб тонких пластин. Оно часто называется уравнением Софи Жермен — Лагранжа.
Видео:Решение уравнения ЛагранжаСкачать

ИЗГИБ ТОНКИХ ПЛАСТИН. ОСНОВНЫЕ ПОНЯТИЯ И ФОРМУЛЫ
Тонкими пластинами, или тонкими плитами (рис. 12.1), принято называть конструктивные элементы, у которых один размер (толщина И) значительно меньше двух других характерных размеров (длины сторон пластины). Поперечная нагрузка q(x,y) вызывает изгиб пластины, который сопровождается появлением поперечных перемещений или прогибов w <x,y).Задача расчета пластин при изгибе в большинстве случаев сводится к определению прогибов при выполнении соответствующих граничных (краевых) условий.
Рис. 12.1. Пластина
Наиболее просто задача расчета пластин решается в рамках так называемой технической теории, которая используется при следующих соотношениях:
где а — длина меньшей из сторон пластины.
Техническая теория изгиба пластин базируется на упрощающих расчет гипотезах, которые, по существу, являются обобщением известных из курса сопротивления материалов гипотез теории изгиба стержней.
Основным уравнением технической теории изгиба пластин является уравнение Софи Жермен — Лагранжа, которое в декартовой системе координат имеет следующий вид:
где D — жесткость пластины при изгибе, определяемая по формуле:
В общем случае изгиба в пластине возникают пять внутренних усилий — изгибающие моменты Мх, Му, крутящий момент Мху = Мух = Н и поперечные силы Qx, Qy (рис. 12.2).
Рис. 12.2. Внутренние усилия: а — изгибающие моменты Мх, Mv; б — крутящие моменты Н в — поперечные силы Qx, Qy
Внутренние усилия определяются по формулам:
Внутренние усилия относятся к единице длины координатных линий. При этом изгибающие и крутящий моменты имеют размерность кНсм/см, а поперечные силы — кН/см и т.п.
Внутренние усилия и распределенная нагрузка q(x,y) связаны между собой следующими дифференциальными зависимостями:
Внутренние усилия являются равнодействующими нормальных и касательных напряжений в сечениях пластины, перпендикулярных к срединной плоскости (рис. 12.3).
Рис. 12.3. Нормальные и касательные напряжения
Нормальные напряжения ох и ау и касательные напряжения тху = тух изменяются по толщине пластины по линейному закону и имеют наибольшие значения при z = ±h/2. Касательные напряжения х2Х и xzy изменяются по толщине по закону квадратной параболы и имеют наибольшие значения в точках на уровне срединной плоскости (z = 0). Эпюры напряжений приведены в задаче 12.1.
Напряжение az, характеризующее взаимное давление между продольными слоями пластины, в большинстве случаев значительно меньше остальных напряжений и в силу этого не учитывается.
Функция прогиба пластины должна удовлетворять граничным условиям, которые зависят от характера закрепления пластины. Рассмотрим три основных типа граничных условий в случае прямоугольных пластин.
Жестко защемленные края (рис. 12.4):
Рис. 12.4. Граничные условия
Шарнирно опертые края (рис. 12.5):
Рис. 12.5. Граничные условия
Свободные от закреплений края (рис. 12.6):
Рис. 12.6. Граничные условия
В приведенных формулах срт и ср^ — углы наклона нормали к срединной плоскости пластины; Vx, Vy — приведенные поперечные силы; тх, ту, р — распределенные краевые нагрузки.
Расчет пластин на прочность производится в точках верхней и нижней поверхностей пластины при 2 = ±h/2, где напряжения сх, Mq и радиальная поперечная сила Q, (рис. 12.8).
Рис. 12.8. Внутренние усилия Внутренние усилия определяются по формулам:
Эти внутренние усилия являются равнодействующими напряжений ог, о0 и xzr = xrz. Характер изменения этих напряжений по толщине пластины показан в задаче 12.3.
Стальная прямоугольная шарнирно опертая пластина находится под действием распределенной поперечной нагрузки, изменяющейся по
Определим внутренние усилия и напряжения в пластине и построим их эпюры. Определим толщину пластины из условий прочности и жесткости.
Рис. 12.9. Шарнирно опертая пластина
В расчетах примем:
а = 150 см; b = 120 см; q0 = 0,01 кН/см 2 ; Е = 2,1 • 10 4 кН/см 2 ; v = 0,3; ус = 1,0; у< = 1,0; Л = 21 кН/см 2 ; wHf>/6 2 ; Е = 2,1 • 10 4 кН/см 2 ; v = 0,3; ус = 1,0; yf= 1,0; R = 21 кН/см 2 ;
Wtfja 4 кН/см 2 ; v = 0,3; ус = yf= 1,0; Л = 21 кН/см 2 ; Я, = 30 см;
R.2 = 60 см; q = 0,01 кН/см 2 ; т = 3 кНсм/см; и>нб Mq имеют наибольшие значения. Используем энергетическую теорию прочности. Условие прочности в точках при z = ±h/2 имеет следующий вид:
Подставив выражения наибольших напряжений через изгибающие моменты, получим:
Поставим условие жесткости на внешнем контуре пластины:
Использовав формулу для жесткости пластины, определим требуемую толщину:
Принимаем с округлением h = 0,9 см.
Значения прогиба, умноженные на жесткость D, приведены в табл. 4. Эпюры внутренних усилий и прогиба приведены на рис. 12.14.
Определим наибольшие нормальные и касательные напряжения в пластине:

Рис. 12.14. Эпюры внутренных усилий и прогиба Эпюры напряжений приведены на рис. 12.15.
Для кольцевых пластин, закрепленных по обоим краям, определение постоянных интегрирования является более громоздким, т.к. необходимо решать систему алгебраических уравнений с тремя или четырьмя неизвестными. В этом случае можно использовать составленную на кафедре программу расчета для ПЭВМ.
Рис. 12.15. Эпюры напряжений: а — эпюры радиальных и кольцевых напряжений; б — эпюра касательных напряжений
- 1. Какие конструктивные элементы принято называть тонкими пластинами (плитами)?
- 2. Какая функция определяется в первую очередь при решении задачи об изгибе пластины под действием поперечной нагрузки?
- 3. Приведите гипотезы технической теории изгиба пластины.
- 4. При каких геометрических соотношениях используется техническая теория изгиба пластин?
- 5. Как записывается основное уравнение технической теории изгиба пластин в декартовой и полярной системах координат?
- 6. Как определяется жесткость пластины при изгибе?
- 7. Какие внутренние усилия возникают в общем случае изгиба прямоугольной пластины? В каких единицах они измеряются?
- 8. Как записываются формулы для определения внутренних усилий в прямоугольной пластине?
- 9. Какими зависимостями связаны между собой внутренние усилия в прямоугольной пластине и распределенная поперечная нагрузка?
- 10. Какие напряжения возникают в сечениях пластины, перпендикулярных к срединной плоскости? Как они связаны с внутренними усилиями? Какой характер их изменения по толщине пластины?
- 11. Какие напряжения не учитываются при решении задач об изгибе пластин?
- 12. Каким условиям должна удовлетворять функция прогиба пластины?
- 13. Как записываются граничные условия для жестко защемленных, шарнирно опертых и свободных от закрепления краев для прямоугольных пластин?
- 14. Как записывается условие прочности пластины?
- 15. Какое условие должно выполняться при расчете пластин на жесткость?
- 16. Какие методы используются для расчета прямоугольных пластин, шарнирно опертых по всем сторонам и по двум противоположным сторонам?
- 17. Какой изгиб круглых и кольцевых пластин называется осесимметричным?
- 18. Какие внутренние усилия возникают в круглых и кольцевых пластинах при осесимметричном изгибе?
- 19. Какой вид имеет дифференциальное уравнение осесимметричного изгиба пластин?
- 20. Как записывается выражение для прогиба пластины при осесимметричном изгибе?
Видео:Уравнение ЛагранжаСкачать

ВЫВОД УРАВНЕНИЯ РАВНОВЕСИЯ ДЛЯ ЭЛЕМЕНТАРНОЙ ЧАСТИ ПЛАСТИНЫ
Сумма сил на вертикальную ось 0Z:
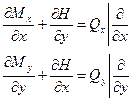
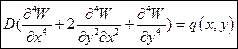
основное дифференциальное уравнение изгиба пластинки, обычно записываемое в виде
Таким образом, расчёт любой пластинки сводится к решению ур-ния Софи Жермен при заданных граничных условиях (услов. закреп. её краёв).
ω – прогиб пластинки
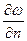
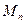
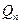
H – крутящий момент
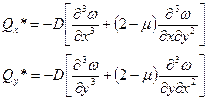
Дата добавления: 2015-08-01 ; просмотров: 2654 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
📽️ Видео
Курс по ОДУ: Уравнения Клеро и Лагранжа | Занятие 8Скачать

9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать

№9. Элементы вариационного исчисления. Уравнения Лагранжа-Эйлера.Скачать

11. Уравнения в полных дифференциалахСкачать

Метод Лагранжа & Метод Бернулли ★ Решение линейных неоднородных дифференциальных уравненийСкачать

Дифференциальное уравнение Лагранжа II рода. Расчет механической системы.Скачать

7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Линейное неоднородное дифференциальное уравнение 2 способаСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать

Уравнение в полных дифференциалахСкачать

Дифференциальное уравнение. Формула ЭйлераСкачать

7. Телеграфные уравненияСкачать

8. Дифференциальные уравнения, линейные относительно х и х'Скачать

Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Видеоурок "Уравнение в полных дифференциалах"Скачать

Дифференциальное уравнение БесселяСкачать