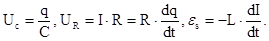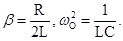Уравнение собственных затухающих колебаний заряда тока в последовательном rlc контуре и его решение (6 видео)

Содержание

Свободные (затухающие) колебания в последовательном RLC-контуре.
Затухающие колебания в контуре и их уравнение
Характеристики затухающих колебаний
Уравнения затухающих колебаний
Затухающие колебания в контуре и их уравнение
Определение, характеристики затухающих колебаний
Готовые работы на аналогичную тему
Уравнение затухающих колебаний
📸 Видео

Видео:RLC контур - свободные колебанияСкачать

Свободные (затухающие) колебания в последовательном RLC-контуре.

Цель работы:наблюдение затухающих колебаний на экране осциллографа и экспериментальное определение характеристик колебаний и параметров контура.

Приборы и принадлежности:генератор прямоугольных импульсов (в блоке ГН1), цифровой осциллограф PicoScope 2203, стенд С-ЭМ01, соединительные провода.

Краткие теоретические сведения:

Уравнение свободных колебаний в последовательном RLC –контуре (рис.1) может быть получено из второго правила Кирхгофа:

где

Окончательно уравнение принимает вид

, (1)

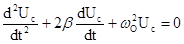
где

Решением уравнения (1) при малом затухании (b 2 2 ) является функция, описываемая уравнением

, (2)

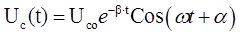
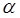
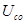
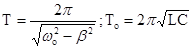
где w-частота затухающих колебаний, b-коэффициент затухания, — начальная фаза, -максимальное напряжение на конденсаторе

Период затухающих колебаний Т при малом затухании можно приближенно считать равным периоду незатухающих колебаний Т₀

. (3)

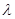
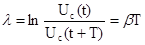
Важной характеристикой затухающих колебаний является логарифмический декремент затухания , характеризующий уменьшение амплитуды колебаний за один период

, (4)

где U_c(t)-амплитуда затухающих колебаний в момент времени t; U_c(t+T)- амплитуда затухающих колебаний через период в момент времени t+T.

При малом затухании (w » w_о) для l можно использовать формулу

, (5)

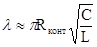
где R_конт— общее активное сопротивление контура.

, (6)

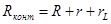
где R – внешнее сопротивление, r – внутренне сопротивление источника тока, 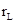— активное сопротивление катушки.

Критическое сопротивление контура, при котором колебательный процесс переходит в апериодический, может быть найдено из условия b_кр=w_о.

. (7)

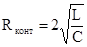
Добротность контура Q равна

. (8)

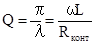
Видео:Урок 361. Вынужденные колебания в последовательном колебательном контуреСкачать

Затухающие колебания в контуре и их уравнение

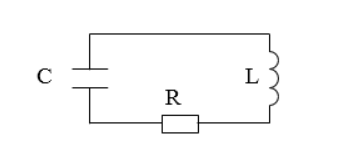
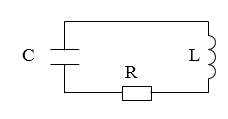
Существуют колебания в системе без источника энергии, называемые затухающими. Рассмотрим реальный контур с сопротивлением не равным нулю. Для примера используют контур с включенным сопротивлением R , с емкостью конденсатора C , с катушкой индуктивности L , изображенный на рисунке 1 . Колебания, происходящие в нем, — затухающие.

Именно наличие сопротивления становится главной причиной их затухания. Данный процесс возможен посредствам потерь энергии на выделение джоулева тепла. Аналог сопротивления в механике – действие сил трения.

Видео:Урок 343. Затухающие колебания (часть 1)Скачать

Характеристики затухающих колебаний

Затухающие колебания характеризуют коэффициентом затухания β . Применив второй закон Ньютона, получим:

m a = — k x — y v , d 2 x d t 2 + r m d x d t + k m x = 0 , ω 0 2 = k m , β = r 2 m .

Из записи видно, что β действительно является характеристикой контура. Реже вместо β применяют декремент затухания δ ,

Значение a ( t ) является амплитудой заряда, силы тока и так далее, δ равняется количеству колебаний, а N e — период времени уменьшения амплитуды в e раз.

Для R L C контура применима формула с ω частотой.

При небольшой δ ≪ 1 говорят, что β ≪ ω 0 ω 0 = 1 L C — собственная частота, отсюда ω ≈ ω 0 .

При рассмотрении затухающих колебаний последовательного контура колебательный контур характеризуется добротностью Q :

Q = 1 R L C = ω 0 L R , где R , L и C — сопротивление, индуктивность, емкость, а ω 0 — частота резонанса. Выражение L C называют характеристическим или волновым сопротивлением. Для параллельного контура формула примет вид:

Q = R L C = R ω 0 L .

R является входным сопротивлением параллельного контура.

Эквивалентное определение добротности применяется при слабых затуханиях. Его выражают через отношение энергий:

Q = ω 0 W P d = 2 π f 0 W P d , называемое общей формулой.

Видео:Резонанс в колебательном контуреСкачать

Уравнения затухающих колебаний

Рассмотрим рисунок 1 . Изменение заряда q на конденсаторе в таком контуре описывается дифференциальным уравнением:

q ( t ) = q 0 e ( — β t ) cos ω t + a ‘ 0 = q 0 e — β t cos ( ω t ) .

Если t = 0 , то заряд конденсатора становится равным q 0 , и ток в цепи отсутствует.

Если R > 2 L C изменения заряда не относят к колебаниям, разряд называют апериодическим.

Значение сопротивления, при котором колебания превращаются в апериодический разряд конденсатора, критическое R k .

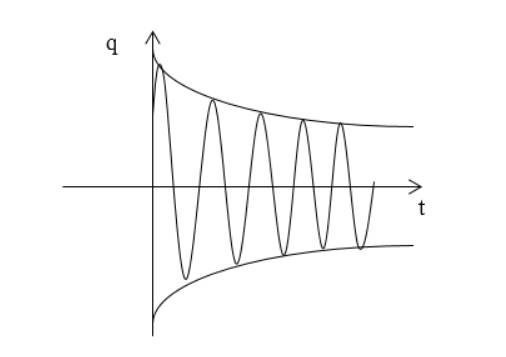
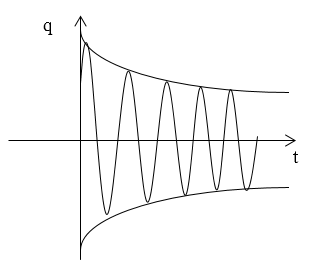
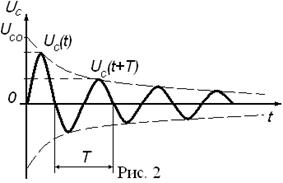
Функция изображается аналогично рисунку 2 .

Записать закон убывания энергии, запасенной в контуре W ( t ) при W ( t = 0 ) = W 0 с затухающими колебаниями. Обозначить коэффициент затухания в контуре β , а собственную частоту — ω 0 .

Решение

Отправная точка решения – это применение формулы изменения заряда на конденсаторе в R L C — контуре:

q ( t ) = q 0 e ( — β t ) cos ω t + a ‘ 0 = q 0 e — β t cos ( ω t ) .

Предположим, что при t = 0 , a ‘ 0 = 0 . Тогда применим выражение

Для нахождения I ( t ) :

I ( t ) = — ω 0 q 0 e ( — 2 β t ) sin ( ω t + α ) , где t g α = β ω .

Очевидно, что электрическая энергия W q запишется как:

W q = q 2 2 C = q 0 2 2 C e ( — 2 β t ) cos 2 ( ω t ) = W 0 e ( — 2 β t ) cos 2 ( ω t ) .

Тогда значение магнитной энергии контура W m равняется:

W m = L 2 ω 0 2 q 0 2 e ( — 2 β t ) sin 2 ω t + a = W 0 e — 2 β t sin 2 ω t + a .

Запись полной энергии будет иметь вид:

W = W q + W m = W 0 e ( — 2 β t ) ( cos 2 ( ω t ) + sin 2 ( ω t + a ) ) = = W 0 e ( — 2 β t ) 1 + β ω 0 sin ( 2 ω t + α ) .

Где sin α = β ω 0 .

Ответ: W ( t ) = W 0 e ( — 2 β t ) 1 + β ω 0 sin ( 2 ω t + a ) .

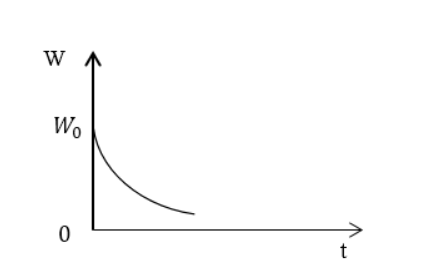
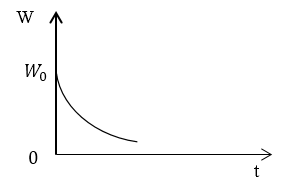
Применив результат предыдущего примера, записать выражение для энергии, запасенной в контуре W ( t ) , при медленно затухающих колебаниях. Начертить график убывания энергии.

Решение

Если колебания в контуре затухают медленно, то:

Очевидно, выражение энергии, запасенной в контуре, вычислим из

W ( t ) = W 0 e ( — 2 β t ) 1 + β ω 0 sin ( 2 ω t + a ) , предварительно преобразовав до W ( t ) = W 0 e ( — 2 β t ) .

Такое упрощение возможно по причине выполнения условия β ω 0 ≪ 1 , sin ( 2 ω t + a ) ≤ 1 , что означает β ω 0 sin ( 2 ω t + a ) ≪ 1 .

Ответ: W ( t ) = W 0 e ( — 2 β t ) . Энергия в контуре убывает по экспоненте.

Видео:Урок 353. Колебательный контурСкачать

Затухающие колебания в контуре и их уравнение

Вы будете перенаправлены на Автор24

Видео:Графические зависимости заряда и силы тока от времени в идеальном колебательном контуре. 11 класс.Скачать

Определение, характеристики затухающих колебаний

В реальном мире любые колебания в системе, где нет источника энергии, являются затухающими. Рассмотрим реальный контур, сопротивление которого отлично от нуля. Примером простейшей системы, которую рассматривают в таком случае может служить контур включают сопротивление $(R)$, конденсатор емкостью $C$, катушку индуктивности $L$, тогда такой контур имеет вид указанный на рис.1. Колебания в таком контуре являются затухающими.

Причиной затухания колебаний в таком контуре является наличие сопротивления. Его существование ведет к тому, что в контуре происходят потери энергии на выделение джоулева тепла. В механике аналогом сопротивления являются силы трения.

Затухающие колебания характеризуют коэффициентом затухания ($beta $), равным:

Из выражения (1) видно, что $beta $ является характеристикой контура. Иногда для характеристики затухания используют логарифмический декремент затухания ($delta $), который равен:

где $aleft(tright)$- амплитуда какой — либо величины (заряда, силы тока и т.д.). $delta $ равен количеству колебаний ($N_e$) за время, в течение которого амплитуда уменьшается в e раз:

Для $RLC$ контура:

где $omega $ — частота.

Если затухание небольшое ($delta ll 1$), то полагают, что $beta ll _0$ ($_0=sqrt<frac>-собственнная частота$), тогда $omega approx _0$. В таком случае:

Рассматривая затухающие колебания, колебательный контур характеризуют его добротностью ($O$). Он равен:

Для слабого затухания добротность можно выразить как:

Также при слабом затухании электрических колебаний добротность можно выразить через отношение энергий:

где $W$ — энергия контура, $triangle W$- уменьшение энергии контура за одно колебание.

Готовые работы на аналогичную тему

Видео:Затухающие колебания. Вынужденные колебания | Физика 9 класс #26 | ИнфоурокСкачать

Уравнение затухающих колебаний

Обратимся вновь к контуру, который изображен на рис.1. Изменение заряда ($q$) на конденсаторе в таком контуре описывается дифференциальным уравнением вида:

где $omega =sqrt<frac-frac> cdot beta =frac$. Амплитуда равна:

В том случае, если при $t=0$ заряд на конденсаторе равен $q_0$, тока в цепи нет, то для $A_0$ можно записать:

Начальная фаза колебаний ($_0$) равна:

При $R >2sqrt<frac>$ изменение заряда не является колебаниями, разряд конденсатора называют апериодическим.

Сопротивление, при котором колебания превращаются в апериодический разряд конденсатора называется критическим ($R_k$). Величина $R_k$ определяют условием:

График функции (10) изображают как на рис.2.

Задание: Запишите закон убывания энергии, запасенной в контуре $(W(t))$, если $W(t=0)=W_0,$ колебания являются затухающими. Коэффициент затухания колебаний в контуре равен $beta $. Собственная частота $_0. $

Решение:

В качестве отправной точки для решения задачи используем уравнение изменения заряда на конденсаторе в $RLC$ -контуре в виде:

в выражении (1.1) мы предположили, что при $t=0, <‘>_0=0$. Используя выражение:

Найдем $I(t)$, получим:

Следовательно, электрическая энергия контура ($W_q$) имеет вид:

Магнитная энергия контура ($W_m$) равна:

Полная энергия равна:

Задание: Используя результат Примера 1, запишите выражение для энергии, запасенной в контуре ($W(t)$), если колебания затухают в контуре очень медленно. Изобразите график убывания энергии запасенной в контуре.

Решение:

Если колебания в контуре затухают медленно, то это значит:

Следовательно, выражение для энергии, запасенной в контуре:

можно преобразовать к виду: