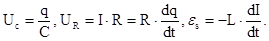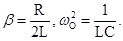Цель работы:
* Знакомство с моделью свободных колебаний в последовательном RLC-контуре.
* Экспериментальное исследование закономерностей свободных незатухающих и затухающих колебаний.
* Экспериментальное определение характеристик затухания в RLC-контуре.
Основные понятия:
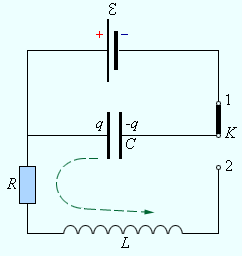
В электрических цепях, так же как и в механических системах, таких как груз на пружине или маятник, могут возникать свободные колебания. Простейшей электрической системой, способной совершать свободные колебания, является последовательный RLC-контур
Закон Ома для замкнутой RLC-цепи, не содержащей внешнего источника тока, записывается в виде
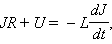
где 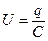

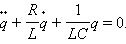
Рассмотрим сначала случай, когда в контуре нет потерь электромагнитной энергии (R = 0). Тогда
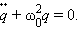
Здесь принято обозначение: 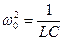
В отсутствие затухания свободные колебания в электрическом контуре являются гармоническими, то есть происходят по закону
Параметры L и C колебательного контура определяют только собственную частоту свободных колебаний
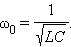
Амплитуда q0 и начальная фаза φ0 определяются начальными условиями, то есть тем способом, с помощью которого система была выведена из состояния равновесия.
При свободных колебаниях происходит периодическое превращение электрической энергии Wэ, запасенной в конденсаторе, в магнитную энергию Wм катушки и наоборот. Если в колебательном контуре нет потерь энергии, то полная электромагнитная энергия системы остается неизменной:
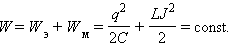
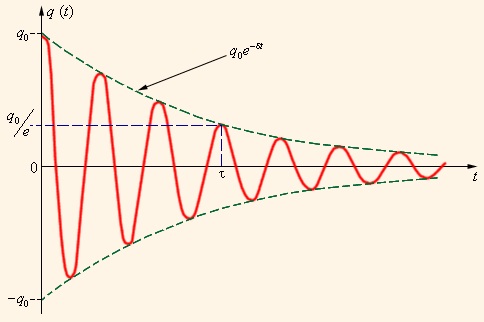
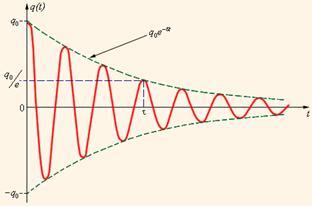
Все реальные контура содержат электрическое сопротивление R. Процесс свободных колебаний в таком контуре уже не подчиняется гармоническому закону. За каждый период колебаний часть электромагнитной энергии, запасенной в контуре, превращается в джоулево тепло, и колебания становятся затухающими (рисунок 2).
Рисунок 2 Затухающие колебания
Затухающие колебания в электрическом контуре аналогичны затухающим колебаниям груза на пружине при наличии вязкого трения, когда сила трения изменяется прямо пропорционально скорости тела: Fтр = – dυ. Коэффициент d в этой формуле аналогичен сопротивлению R в электрическом контуре. Уравнение свободных колебаний в контуре при наличии затухания имеет вид
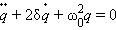
Физическая величина δ = R / 2L называется коэффициентом затухания. Решением этого дифференциального уравнения является функция
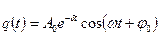
где 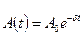
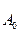
Скорость затухания зависит от электрического сопротивления R контура. Интервал времени 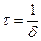
в течение которого амплитуда колебаний уменьшается в e ≈ 2,7 раза, называется временем затухания.
Для характеристики степени затухания в контуре, кроме величины δ, вводят понятие логарифмического декремента затухания q. Он равен натуральному логарифму отношения двух последующих амплитуд (отстоящих во времени на один период)
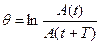
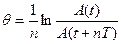

Добротность Q колебательной системы вычисляется:
Добротности Q любой колебательной системы, способной совершать свободные колебания, может быть дано энергетическое определение:
Для RLC-контура добротность Q выражается формулой
Добротность электрических контуров, применяемых в радиотехнике, обычно порядка нескольких десятков и даже сотен.
Следует отметить, что собственная частота ω свободных колебаний в контуре с не очень высокой добротностью несколько меньше собственной частоты ω0 идеального контура с теми же значениями L и C. Но при Q ≥ (5 – 10) этим различием можно пренебречь.
Расчетные формулы:
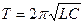
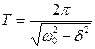
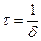
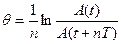
добротность RLC-контура: 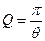
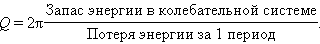
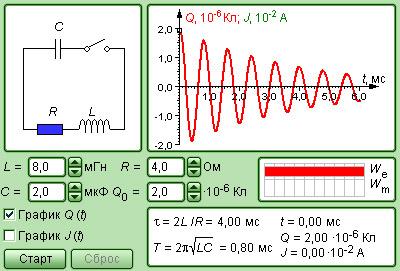
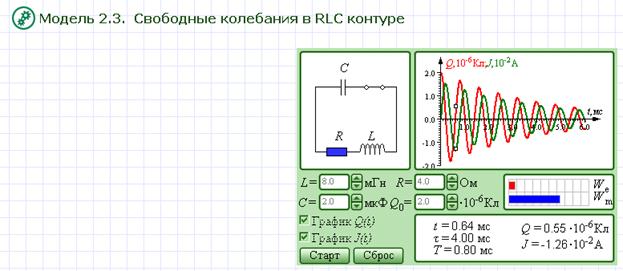
Перейдите от окна теории к окну модели, щелкнув по изображению «Модель. Свободные колебания в RLC-контуре». Внимательно рассмотрите рисунок, найдите все регуляторы и другие основные элементы.
Нажмите кнопку «Старт».Пронаблюдайте картину затухающих колебаний в RLC-контуре. Установите значение R=0. Пронаблюдайте картину незатухающих колебаний. Получите у преподавателя допуск для выполнения измерений.
Порядок измерений и обработка результатов:
ЭКСПЕРИМЕНТ 1. Определение периода затухающих и незатухающих колебаний.
- Установите значение L и C, соответствующее вашей бригаде. Установите значение R=0.
- Выберите график Q(t) (для бригад 1-4), выберите график I(t) (для бригад 5-8), нажмите кнопку «Старт». Нажимая кнопку «Стоп», засеките время n полных колебаний, где n=1 — 7.
- Рассчитайте период колебаний
для каждого значения n. Вычислите среднее значение периода.
- Рассчитайте период колебаний, исходя из параметров RLC-контура
.
- Сравните значения периода, полученные в пп. 3 и 4 со значением периода, выведенным на экране.
- Повторите измерения и расчеты пп. 2-5 для незатухающих колебаний, установив значение R, соответствующее вашей бригаде.
ТАБЛИЦА 1. Параметры RLC-контура (не перерисовывать)
| Бригада |
| L [мГн] |
| C [мкФ] |
| R[Ом] |
ТАБЛИЦА 2. Результаты измерений при L= ____ мГн, C = ____ мкФ, R=0 Ом.
| n | ti, с | 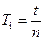 , с , с |
| T ср=____с |
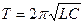
ТАБЛИЦА 3. Результаты измерений при L= ____ мГн, C = ____ мкФ, R=____ Ом.
| n | ti, с | 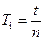 , с , с |
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| T ср=____с |
t =____с, 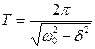
ЭКСПЕРИМЕНТ 2 Определение логарифмического декремента затухания.
- Выберите график q(t).
- Запишите значение
. Измерьте с помощью линейки (или нажимая кнопку «Стоп») амплитуду колебаний через n=3 полных колебаний
.
- Рассчитайте логарифмический декремент затухания
.
- Повторите измерения пп. 2-3 еще 3 раза.
- Рассчитайте среднее значение логарифмического декремента затухания.
- Рассчитайте логарифмический декремент затухания по формуле
.
- Сравните полученные результаты.
ТАБЛИЦА 4. Логарифмический декремент затухания
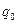 = = 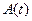 | 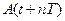 | 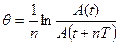 |  |
ЭКСПЕРИМЕНТ 3 Определение добротности контура.
- Определите начальную энергию RLC-контура W0, нажмите кнопку «Старт». Нажимая кнопку «Стоп», определите энергию через одно полное колебание W1.
- Рассчитайте потерю энергии за один период
.
- Рассчитайте добротность
.
- Повторите измерения полной энергии через период W2, W3, W4, W5, каждый раз вычисляя потерю энергии за период
и добротность
- Рассчитайте среднее значение Q.
- Сравните полученный результат с результатом расчетной формулы
.
- Вычислите добротность контура по формуле
ТАБЛИЦА 5. Добротность контура
Видео:Урок 347. Вынужденные колебания. Резонанс (часть 1)Скачать

RLC-контур. Свободные колебания
Видео:Урок 353. Колебательный контурСкачать

R L C -контур
Кроме как в механических системах, к примеру, в таких, маятник или же грузило на пружине, свободные колебания могут возникать также и в электрических цепях, самым простым примером чего может послужить последовательный R L C -контур, изображенный на рис. 2 . 2 . 1 .
Рисунок 2 . 2 . 1 . Последовательный R L C -контур.
Находясь в положении 1 , ключ К позволяет источнику зарядить конденсатор до некоего напряжения δ . Процесс разрядки ранее заряженного конденсатора провоцируется переключением ключа К во второе положение и происходит через катушку индуктивности L и резистор R . При выполнении определенных условий данный процесс может приобретать характер колебательного.
Для не содержащей внешнего источника тока замкнутой R L C -цепи закон Ома представляет из себя выражение:
J R + U = — L d J d t .
В данной формуле U = q C – напряжение на конденсаторе, q является обозначением заряда конденсатора, а J = d q d t – ток в цепи. Правой частью соотношения является выражение ЭДС самоиндукции катушки. В случае, когда заряд конденсатора q ( t ) берется как переменная величина, описывающее свободные колебания в R L C -контуре уравнение может быть приведено к виду:
q · · + R L q · + 1 L C q = 0 .
Для начала рассмотрим такую ситуацию, в которой электромагнитные потери энергии в контуре равны нулю. В таком случае:
q · · + ω 0 2 q = 0 .
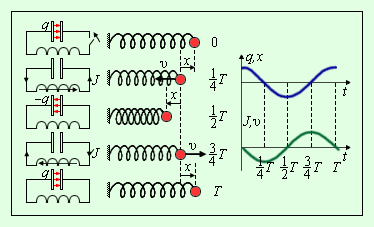
Примем обозначение ω 0 2 = 1 L C . Данным чуть выше уравнением описывается процесс незатухающих свободных колебаний в L C — контуре. Внешне оно полностью эквивалентно уравнению свободных колебаний груза на пружине в условиях отсутствующих сил трения. Аналогичный свободным механическим и электрическим колебаниям процесс изображен на рисунке 2 . 2 . 2 . На данной иллюстрации приводятся графики зависимости заряда смещения x ( t ) груза и q ( t ) конденсатора от положения равновесия, а также графики изменений тока J ( t ) и скорости груза υ ( t ) за период T = 2 π ω 0 колебаний.
Рисунок 2 . 2 . 2 . Аналогия процессов свободных электрических и механических колебаний.
Сделать заключение о некой связи между механическими и электрическими величинами нам позволяет сопоставление процессов в электрическом колебательном контуре и свободных колебаний груза на пружине. Данные аналогии показаны в таблице.
| Электрические величины | Механические величины | ||
| Заряд конденсатора | q ( t ) | Координата | x ( t ) |
| Ток в цепи | J = d q d t | Скорость | ν = d x d t |
| Индуктивность | L | Масса | m |
| Величина, обратная электроемкости | 1 C | Жесткость | k |
| Напряжение на конденсаторе | U = q C | Упругая сила | k x |
| Энергия электрического поля конденсатора | q 2 2 C | Потенциальная энергия пружины | k x 2 2 |
| Магнитная энергия катушки | L I 2 2 | Кинетическая энергия | m ν 2 2 |
| Магнитный поток | L I | Импульс | m υ |
Видео:RLC контур - свободные колебанияСкачать

Свободные колебания
Свободные колебания в электрическом контуре носят название гармонических при условии отсутствия затухания.
Такие колебания происходят по закону:
q ( t ) = q 0 cos ( ω t + φ 0 ) .
Параметры L и C колебательного контура определяют лишь собственную частоту свободных колебаний:
«Начальными условиями», определяющими амплитуду q 0 и начальную фазу φ 0 , называют тот способ, при помощи которого систему вывели из равновесия.
Например, для процесса колебаний, который начнется в контуре, изображенном на рисунке 2 . 2 . 1 , после перевода ключа K в второе положение, q 0 = C δ , φ 0 = 0 .
Процесс свободных колебаниях провоцирует повторяющееся превращение запасенной в конденсаторе электрической энергии W э в магнитную энергию катушки W м и наоборот. В ситуации, когда потери энергии равны нулю, полная электромагнитная энергия системы не претерпевает изменений:
W = W э + W м = q 2 2 C + L J 2 2 = c o n s t
Однако любой реально существующий контур, в отличие от идеального, включает в себя некоторое сопротивление R . По этой причине, процесс свободных колебаний в подобном контуре не подчиняется гармоническому закону. Запасенная в контуре энергия с каждым периодом колебаний теряется, превращаясь в джоулево тепло, из-за чего колебания становятся затухающими (рис. 2 . 2 . 3 ).
Рисунок 2 . 2 . 3 . Затухающие колебания в контуре.
Затухающие колебания в электрическом контуре сравнимы с затухающими колебаниями груза на пружине в условиях существующего вязкого трения, при котором сила трения меняет свое значение прямо пропорционально скорости тела: F т р = – β υ .
В данной формуле сопротивление R электрического контура аналогично коэффициенту β . Уравнение свободных колебаний в контуре при наличии затухания принимает следующий вид:
q · · + 2 δ q · + ω 0 2 q = 0
Коэффициентом затухания называется физическая величина δ = R 2 L .
Следующая функция представляет собой решение приведенного выше дифференциального уравнения:
q ( t ) = q 0 e — δ t cos ( ω t + φ 0 ) ,
Также она содержит описывающий затухание колебаний множитель e x p ( – δ t ) . Скорость затухания зависит от электрического сопротивления R контура.
Интервал времени τ = 1 δ , в течение которого амплитуда колебаний уменьшается в e ≈ 2 , 7 раза, называется временем затухания.
Понятие добротности Q колебательной системы:
где N является числом полных колебаний, которые совершает система за время затухания τ .
Любая добротность Q , относящаяся к колебательной системе, которая способна совершать свободные колебания, имеет следующее энергетическое определение:
Q = 2 π З а п а с э н е р г и и в к о л е б а т е л ь н о й с и с т е м е П о т е р я э н е р г и и з а 1 п е р и о д
Добротность Q , принадлежащая R L C -контуру, выражают формулой:
Добротность электрических контуров, которые применяются в радиотехнике, обычно порядка нескольких десятков и даже сотен.
Стоит обратить внимание на то, что собственная частота ω свободных колебаний в контуре с не самой высокой добротностью несколько уступает собственной частоте ω 0 идеального контура с такими же значениями L и C . Однако при Q ≥ ( 5 ÷ 10 ) данным различием можно пренебречь.
Рисунок 2 . 2 . 4 . Модель свободных колебаний в R L C -контуре.
Видео:Физика 11 класс (Урок№7 - Свободные и вынужденные электромагнитные колебания. Колебательный контур.)Скачать

Свободные (затухающие) колебания в последовательном RLC-контуре.
Цель работы:наблюдение затухающих колебаний на экране осциллографа и экспериментальное определение характеристик колебаний и параметров контура.
Приборы и принадлежности:генератор прямоугольных импульсов (в блоке ГН1), цифровой осциллограф PicoScope 2203, стенд С-ЭМ01, соединительные провода.
Краткие теоретические сведения:

где
Окончательно уравнение принимает вид
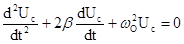
где
Решением уравнения (1) при малом затухании (b 2 2 ) является функция, описываемая уравнением
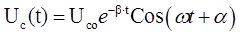
где w-частота затухающих колебаний, b-коэффициент затухания, 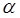
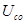
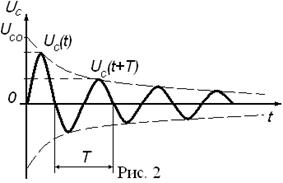
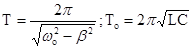
Важной характеристикой затухающих колебаний является логарифмический декремент затухания 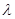
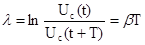
где Uc(t)-амплитуда затухающих колебаний в момент времени t; Uc(t+T)- амплитуда затухающих колебаний через период в момент времени t+T.
При малом затухании (w » wо) для l можно использовать формулу
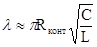
где Rконт— общее активное сопротивление контура.
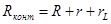
где R – внешнее сопротивление, r – внутренне сопротивление источника тока, 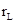
Критическое сопротивление контура, при котором колебательный процесс переходит в апериодический, может быть найдено из условия bкр=wо.
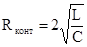
Добротность контура Q равна
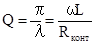
📹 Видео
Свободные электромагнитные колебания. 11 класс.Скачать

Урок 361. Вынужденные колебания в последовательном колебательном контуреСкачать

RLC контур - вынужденные колебанияСкачать

Резонанс в колебательном контуреСкачать

Колебательный контур. Получение электромагнитных колебаний | Физика 9 класс #45 | ИнфоурокСкачать

Урок 335. Анализ графика гармонических колебанийСкачать

Билеты №45 "Вынужденные колебания в линейных системах"Скачать

19 Колебательный контур.Скачать

Вынужденные электромагнитные колебания. Автоколебания. 11 класс.Скачать

🚀 РЕЗОНАНСНАЯ ✈️ БЕСПЛАТНАЯ ⚡⚡⚡ ЭНЕРГИЯ от МОТ ТрансформатораСкачать

Лекция №15 "Вынужденные колебания в контуре"Скачать

Вынужденные колебания. Резонанс | Физика 11 класс #9 | ИнфоурокСкачать

КАК РАБОТАЕТ КОЛЕБАТЕЛЬНЫЙ КОНТУРСкачать

Колебательный контур | ЕГЭ Физика | Николай НьютонСкачать

Тема 8. Колебательный контур. Свободные электромагнитные колебания в контуре. Формула ТомсонаСкачать

Резонанс LC на практикеСкачать

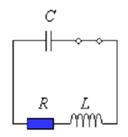
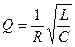
 для каждого значения n. Вычислите среднее значение периода.
для каждого значения n. Вычислите среднее значение периода.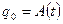 . Измерьте с помощью линейки (или нажимая кнопку «Стоп») амплитуду колебаний через n=3 полных колебаний
. Измерьте с помощью линейки (или нажимая кнопку «Стоп») амплитуду колебаний через n=3 полных колебаний 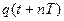 .
.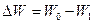 .
.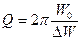 .
.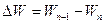 и добротность
и добротность 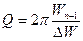
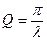 .
.