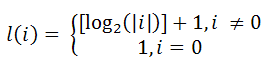Уравнение сложности некоторого алгоритма f n 4n 2 2n n асимптотическая сложность будет (6 видео)

Оценка сложности алгоритмов

Содержание

Введение
Определения
Порядок роста сложности алгоритмов
Виды асимптотических оценок
Критерии оценки сложности алгоритмов
Пример оценки сложности при вычислении факториала
Асимптотический анализ алгоритмов.
Асимптотическая сложность алгоритмов: что за зверь?
📽️ Видео

Введение

Для любого программиста важно знать основы теории алгоритмов, так как именно эта наука изучает общие характеристики алгоритмов и формальные модели их представления. Ещё с уроков информатики нас учат составлять блок-схемы, что, в последствии, помогает при написании более сложных задач, чем в школе. Также не секрет, что практически всегда существует несколько способов решения той или иной задачи: одни предполагают затратить много времени, другие ресурсов, а третьи помогают лишь приближённо найти решение.

Всегда следует искать оптимум в соответствии с поставленной задачей, в частности, при разработке алгоритмов решения класса задач.
Важно также оценивать, как будет вести себя алгоритм при начальных значениях разного объёма и количества, какие ресурсы ему потребуются и сколько времени уйдёт на вывод конечного результата.
Этим занимается раздел теории алгоритмов – теория асимптотического анализа алгоритмов.

Предлагаю в этой статье описать основные критерии оценки и привести пример оценки простейшего алгоритма. На Хабрахабре уже есть статья про методы оценки алгоритмов, но она ориентирована, в основном, на учащихся лицеев. Данную публикацию можно считать углублением той статьи.

Определения

Основным показателем сложности алгоритма является время, необходимое для решения задачи и объём требуемой памяти.
Также при анализе сложности для класса задач определяется некоторое число, характеризующее некоторый объём данных – размер входа.
Итак, можем сделать вывод, что сложность алгоритма – функция размера входа.
Сложность алгоритма может быть различной при одном и том же размере входа, но различных входных данных.

Существуют понятия сложности в худшем, среднем или лучшем случае. Обычно, оценивают сложность в худшем случае.

Временная сложность в худшем случае – функция размера входа, равная максимальному количеству операций, выполненных в ходе работы алгоритма при решении задачи данного размера.
Ёмкостная сложность в худшем случае – функция размера входа, равная максимальному количеству ячеек памяти, к которым было обращение при решении задач данного размера.

Порядок роста сложности алгоритмов

Порядок роста сложности (или аксиоматическая сложность) описывает приблизительное поведение функции сложности алгоритма при большом размере входа. Из этого следует, что при оценке временной сложности нет необходимости рассматривать элементарные операции, достаточно рассматривать шаги алгоритма.

Шаг алгоритма – совокупность последовательно-расположенных элементарных операций, время выполнения которых не зависит от размера входа, то есть ограничена сверху некоторой константой.

Виды асимптотических оценок

O – оценка для худшего случая

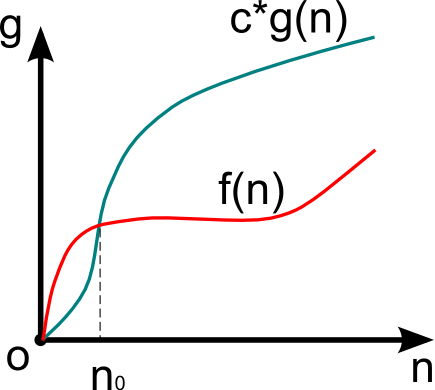
Рассмотрим сложность f(n) > 0, функцию того же порядка g(n) > 0, размер входа n > 0.
Если f(n) = O(g(n)) и существуют константы c > 0, n₀ > 0, то
0 n₀.

Функция g(n) в данном случае асимптотически-точная оценка f(n). Если f(n) – функция сложности алгоритма, то порядок сложности определяется как f(n) – O(g(n)).

Данное выражение определяет класс функций, которые растут не быстрее, чем g(n) с точностью до константного множителя.

Примеры асимптотических функций

f(n)	g(n)
2n 2 + 7n — 3	n 2
98n*ln(n)	n*ln(n)
5n + 2	n
8	1

Ω – оценка для лучшего случая

Определение схоже с определением оценки для худшего случая, однако
f(n) = Ω(g(n)), если
0 n₀ всюду находится между c₁*g(n) и c₂*g(n), где c – константный множитель.
Например, при f(n) = n 2 + n; g(n) = n 2 .

Критерии оценки сложности алгоритмов

Равномерный весовой критерий (РВК) предполагает, что каждый шаг алгоритма выполняется за одну единицу времени, а ячейка памяти за одну единицу объёма (с точностью до константы).
Логарифмический весовой критерий (ЛВК) учитывает размер операнда, который обрабатывается той или иной операцией и значения, хранимого в ячейке памяти.

Временная сложность при ЛВК определяется значением l(O_p), где O_p – величина операнда.
Ёмкостная сложность при ЛВК определяется значением l(M), где M – величина ячейки памяти.

Пример оценки сложности при вычислении факториала

Необходимо проанализировать сложность алгоритма вычисление факториала. Для этого напишем на псевдокоде языка С данную задачу:

Временная сложность при равномерном весовом критерии

Достаточно просто определить, что размер входа данной задачи – n.
Количество шагов – (n — 1).

Таким образом, временная сложность при РВК равна O(n).

Временная сложность при логарифмическом весовом критерии

В данном пункте следует выделить операции, которые необходимо оценить. Во-первых, это операции сравнения. Во-вторых, операции изменения переменных (сложение, умножение). Операции присваивания не учитываются, так как предполагается, что она происходят мгновенно.

Итак, в данной задаче выделяется три операции:

Видео:Оценка сложности алгоритма. Сложность алгоритмов. Big O, Большое ОСкачать

Асимптотический анализ алгоритмов.

Анализ сравнения затрат времени алгоритмов, выполняемых решение экземпляра некоторой задачи, при больших объемах входных данных, называется асимптотическим. Алгоритм, имеющий меньшую асимптотическую сложность, является наиболее эффективным.

В асимптотическом анализе, сложность алгоритма – это функция, позволяющая определить, как быстро увеличивается время работы алгоритма с увеличением объёма данных.

Основные оценки роста, встречающиеся в асимптотическом анализе:

Ο (О-большое) – верхняя асимптотическая оценка роста временной функции;
Ω (Омега) – нижняя асимптотическая оценка роста временной функции;
Θ (Тета) – нижняя и верхняя асимптотические оценки роста временной функции.

Пусть n – величина объема данных. Тогда рост функции алгоритма f(n) можно ограничить функций g(n) асимптотически:

Обозначение	Описание
f(n) ∈ Ο(g(n))	f ограничена сверху функцией g с точностью до постоянного множителя
f(n) ∈ Ω(g(n))	f ограничена снизу функцией g с точностью до постоянного множителя
f(n) ∈ Θ(g(n))	f ограничена снизу и сверху функцией g

Например, время уборки помещения линейно зависит от площади этого самого помещения (Θ(S)), т. е. с ростом площади в n раз, время уборки увеличиться также в n раз. Поиск имени в телефонной книге потребует линейного времени Ο(n), если воспользоваться алгоритмом линейного поиска, либо времени, логарифмически зависящего от числа записей (Ο(log₂(n))), в случае применения двоичного поиска.

Для нас наибольший интерес представляет Ο-функция. Кроме того, в последующих главах, сложность алгоритмов будет даваться только для верхней асимптотической границы.

Под фразой «сложность алгоритма есть Ο(f(n))» подразумевается, что с увеличением объема входных данных n, время работы алгоритма будет возрастать не быстрее, чем некоторая константа, умноженная на f(n).

Важные правила асимптотического анализа:

O(k*f) = O(f) – постоянный множитель k (константа) отбрасывается, поскольку с ростом объема данных, его смысл теряется, например:

O(9,1n) = O(n)

O(f*g) = O(f)*O(g) – оценка сложности произведения двух функций равна произведению их сложностей, например:

O(5n*n) = O(5n)*O(n) = O(n)*O(n) = O(n*n) = O(n 2 )

O(5n/n) = O(5n)/O(n) = O(n)/O(n) = O(n/n) = O(1)

O(f+g) равна доминанте O(f) и O(g) – оценка сложности суммы функций определяется как оценка сложности доминанты первого и второго слагаемых, например:

O(n 5 +n 10 ) = O(n 10 )

Подсчет количества операций – дело утомительное и, что важно, совсем не обязательное. Исходя из выше перечисленных правил, чтобы определить сложность алгоритма, не нужно, как мы это делали прежде, считать все операции, достаточно знать какой сложностью обладает та или иная конструкция алгоритма (оператор или группа операторов). Так, алгоритм, не содержащий циклов и рекурсий, имеет константную сложность O(1). Сложность цикла, выполняющего n итераций, равна O(n). Конструкция их двух вложенных циклов, зависящих от одной и той же переменной n, имеет квадратичную сложность O(n 2 ).

Вот наиболее часто встречающиеся классы сложности:

O(1) – константная сложность;
О(n) – линейная сложность;
О(nа ) – полиномиальная сложность;
О(Log(n)) – логарифмическая сложность;
O(n*log(n)) – квазилинейная сложность;
O(2 n ) – экспоненциальная сложность;
O(n!) – факториальная сложность.

Видео:ВСЯ СЛОЖНОСТЬ АЛГОРИТМОВ ЗА 11 МИНУТ | ОСНОВЫ ПРОГРАММИРОВАНИЯСкачать

Асимптотическая сложность алгоритмов: что за зверь?

Асимптотическая сложность алгоритмов встречается повсеместно. Доступно рассказываем, что это такое, где и как используется.

Асимптотическая сложность алгоритмов представляет собой время и память, которые понадобятся вашей программе в процессе работы. Одно дело – знать, что существуют линейные или логарифмические алгоритмы, но совсем другое – понимать, что же за всем этим стоит.

С помощью Big O Notation можно математически описать то, как поведет себя программа в условиях наихудшего сценария при большом количестве входных данных. Например, если вы используете сортировку пузырьком, чтобы отсортировать элементы в целочисленном массиве по возрастанию, то худшим сценарием в этом случае будет отсортированный в убывающем порядке массив. При таком раскладе вашему алгоритму понадобится наибольшее количество операций и памяти.

Разобравшись в принципе работы Big O Notation, вы сможете решить проблему оптимизации ваших программ и добиться максимально эффективного кода.

Сложности О(1) и O(n) самые простые для понимания.

О(1) означает, что данной операции требуется константное время. Например, за константное время выполняется поиск элемента в хэш-таблице, так как вы напрямую запрашиваете какой-то элемент, не делая никаких сравнений. То же самое относится к вызову i-того элемента в массиве. Такие операции не зависят от количества входных данных.

В случае, если у вас не очень удачная хэш-функция, которая привела к большому количеству коллизий, поиск элемента может занять О(n) , где n – это количество объектов в хэш-таблице. В худшем случае Вам понадобится сделать n сравнении, а именно пройтись по всем элементам структуры. Очевидно, что скорость линейных алгоритмов, то есть алгоритмов, работающих в О(n) , зависит от количества входных данных. В случае с линейными алгоритмами в худшем случае вам придется провести какую-то операцию с каждый элементом.

Бинарный поиск является одним из классических примеров алгоритмов, работающих за O(log_2(n)) . Каждая операция уменьшает количество входных данных вдвое.

Например, если у вас есть отсортированный массив, насчитывающий 8 элементов, в худшем случае вам понадобится сделать Log_2(8)=3 сравнений, чтобы найти нужный элемент.

Рассмотрим отсортированный одномерный массив с 16 элементами:

Допустим, нам нужно найти число 13.

Мы выбираем медиану массива и сравниваем элемент под индексом 7 с числом 13.

Так как наш массив отсортирован, а 16 больше, чем 13, мы можем не рассматривать элементы, которые находятся под индексом 7 и выше. Так мы избавились от половины массива.

Дальше снова выбираем медиану в оставшейся половине массива.

Сравниваем и получаем, что 8 меньше, чем 13. Уменьшаем массив вдвое, выбираем элемент посередине и делаем еще одно сравнение. Повторяем процесс, пока не останется один элемент в массиве. Последнее сравнение возвращает нужный элемент. Лучшее развитие событий – если первая выбранная медиана и есть ваше число. Но в худшем случае вы совершите log_2(n) сравнений.

Сложность O(n*log n) можно представить в виде комбинации O(log n) и O(n) . Такую сложность можно получить, если в вашей программе есть один for-цикл, который содержит еще один for-цикл. То есть нестинг циклов, один из которых работает за O(log n) , а другой – за O(n) .

Сложность O(n^2) встречается довольно часто в алгоритмах сортировки. Ее легко можно получить, если в программе имплементировать нестинг двух for-циклов, работающих в O(n) .

То же самое произойдет, если вам надо будет пройтись по элементам двумерного массива.

Алгоритмы, которые можно описать с помощью нотации O(n^2 + n + 3) или O(n^2-100000) , или даже O(n^2 + 100000000) все равно считаются квадратными. При большом количестве входных данных только наибольшая степень n является важной. Константы и коэффициенты обычно не берут во внимание. То же самое касается линейных и логарифмических функций. O( n +1000) и O(1000*n) все равно будут работать в O(n) .

Использование алгоритмов, которые работают в O(n^2) и выше (например, экспоненциальная функция 2^n ), является плохой практикой. Следует избегать подобных алгоритмов, если хотите, чтобы ваша программа работала за приемлемое время и занимала оптимальное количество памяти.