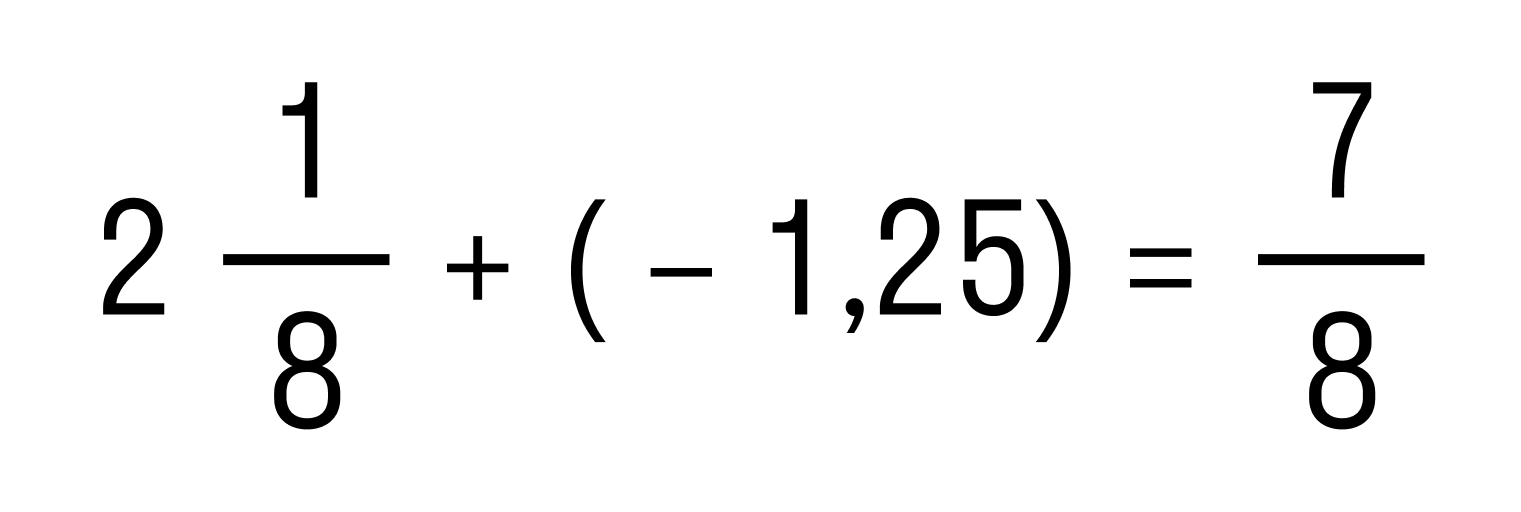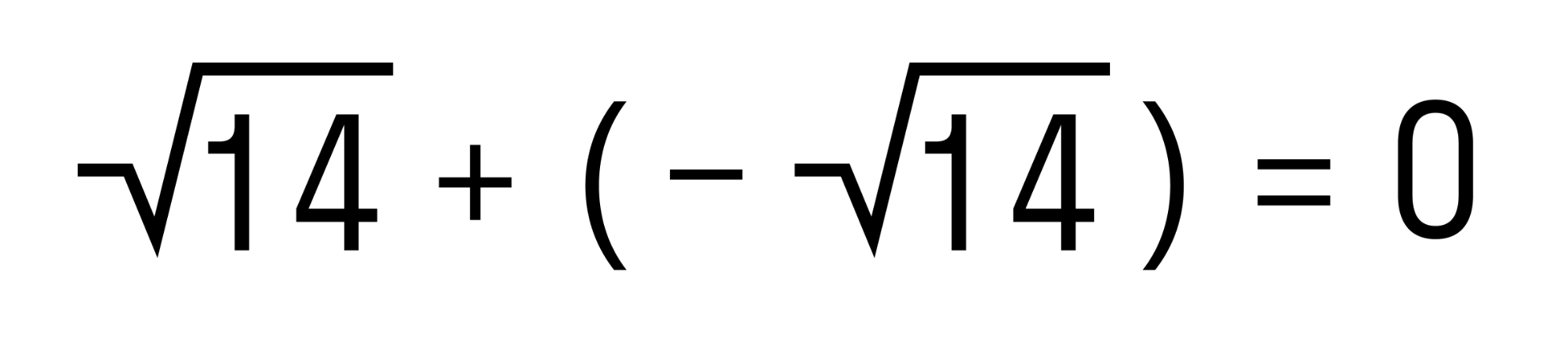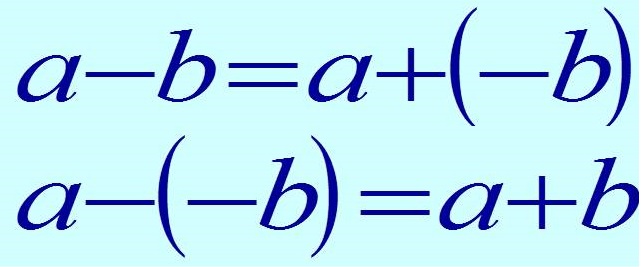О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
- Основные определения
- Правило сложения чисел с разными знаками
- Примеры сложения чисел с разными знаками
- Сложение чисел с разными знаками: правило, примеры
- Основное правило сложения положительных и отрицательных чисел
- Задачи на сложение положительного числа с отрицательным
- Сложение и вычитание отрицательных и положительных чисел — правило, формулы и примеры
- Правило сложения отрицательных чисел и чисел с разными знаками
- Как вычитать отрицательные и положительные числа
- Заключение
- 🌟 Видео
Видео:6 класс, 33 урок, Сложение чисел с разными знакамиСкачать

Основные определения
Целые числа — это множество чисел, которые состоят из натуральных чисел, целых отрицательных чисел и нуля.
Отрицательные целые числа — это целые числа со знаком «минус». Они всегда меньше нуля. Примеры целых отрицательных чисел: -1, -945, -20.
Положительные целые числа — это целые числа со знаком «плюс». Они всегда больше нуля. Примеры положительных целых чисел: 11, 500, 1387.
У каждого положительного числа есть число-близнец, которое отличается только тем, что перед ним стоит знак минус. Такие числа называются противоположными.
Противоположные числа не равны друг другу, но у них есть общее — модуль. Модуль у противоположных чисел одинаковый: у положительного числа он равен самому числу, а у отрицательного — противоположному, то есть положительному. Например:
Действительные числа — это числа, которые могут быть записаны в виде конечной или бесконечной десятичной дроби.
Рациональные числа — это числа, которые можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль.
Видео:как ЛЕГКО сложить отрицательные числа , ПРИМЕРЫСкачать
Правило сложения чисел с разными знаками
Положительное число можно рассматривать как доход, а отрицательное — как расходы или долг. Чтобы понять, сколько мы заработали или потратили, нужно смотреть на модули этих чисел.
Например, родители выдали триста рублей на карманные расходы. Если в конце недели у нас осталось немного денег — значит расходов было меньше, чем дохож. А если нам пришлось попросить еще 50 рублей на наклейки — расходы привысили доход. Если же расходы равны доходам, то у нас будет нулевой остаток.
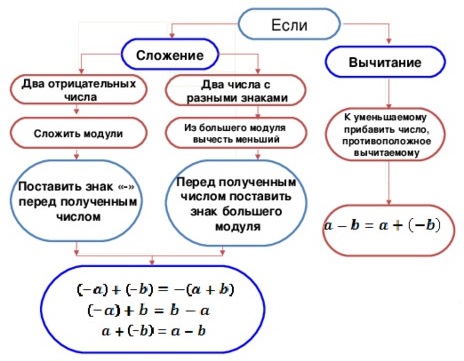
А теперь сформулируем правило сложения чисел с разными знаками.
Чтобы сложить положительное и отрицательное число, нужно:
- Найти модули слагаемых — то есть этих чисел.
- Сравнить полученные числа.
Если они равны, то исходные слагаемые противоположны друг другу (те самые близнецы) — их сумма равна нулю. А если же числа не равны, то нужно запомнить знак числа, модуль которого больше. - Из большего модуля вычесть меньший.
- Перед полученным числом поставить знак того слагаемого, модуль которого больше.
Это правило сводит сложение чисел с разными знаками к вычитанию из большего положительного числа меньшее число. В результате сложения положительного и отрицательного числа может получиться: положительное число, отрицательное число или нуль.
Вот, как выглядит эта последовательность на примере 2 + (-6) = -4:
| Знаки слагаемых | Знак суммы | Модули слагаемых | Модуль суммы | Разность модулей слагаемых | Сравнение знака суммы со знаками слагаемых |
| Разные | «−» | ∣2∣ = 2 ∣-6∣ = 6 | ∣-4∣ = 4 | ∣-6∣ — ∣2∣ = 4 6 — 2 = 4 | Знак результата (-4) такой же, как и у числа, которое больше по модулю (-6) |
Повторим еще раз. Чтобы сложить числа с разными знаками:
- из большего модуля вычесть меньший модуль;
- в результате поставить знак слагаемого с большим модулем.
Алгоритм сложения чисел с разными знаками справедлива для целых чисел, для рациональных чисел и для действительных чисел.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Видео:Сложение и вычитание рациональных чисел. 6 класс.Скачать

Примеры сложения чисел с разными знаками
Сложение чисел с разными знаками требует внимательности и последовательности. Рассмотрим примеры по правилу выше:
Пример 1. Сложить числа -8 и 1.
Нам нужно сложить числа с разными знаками. Выполним все шаги по правилу сложения положительного и отрицательного числа.
- Сначала найдем модули слагаемых, они равны 8 и 1 соответственно.
- Модуль числа -8 больше, чем модуль числа 1. Запомним знак минус.
Теперь от большего модуля отнимаем меньший модуль:
8 — 1 = 7. - Осталось поставить знак минус перед полученным числом, получаем ответ: -7.
На этом сложение чисел с разными знаками завершено.
Пример 2. Сложить положительное число 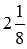
Чтобы сложить рациональные числа с разными знаками, которые не являются целыми, их следует представить в виде обыкновенных или десятичных дробей.
- Представим числа в виде обыкновенных дробей.
Для этого выполним переход от смешанного числа к неправильной дроби:, и переводим десятичную дробь в обыкновенную:
- Теперь можно воспользоваться правилом сложения чисел с разными знаками.
Модули складываемых чисел равны 17/8 и 5/4. Чтобы нам было удобнее считать, приведем дроби к общему знаменателю — получаем 17/8 и 10/8. - Сравним обыкновенные дробей 17/8 и 10/8.
Так как 17>10, то. Это значит, что слагаемое со знаком плюс имеет больший модуль, поэтому запоминаем знак плюс.
- Теперь из большего модуля вычитаем меньший, то есть, выполним вычитание дробей с одинаковыми знаменателями:
Осталось перед полученным числом поставить знак плюс, получаем:, то есть 7/8.
На этом сложение чисел с разными знаками завершено. Краткая запись решения выглядит так:
Пример 3. Чему равна сумма чисел 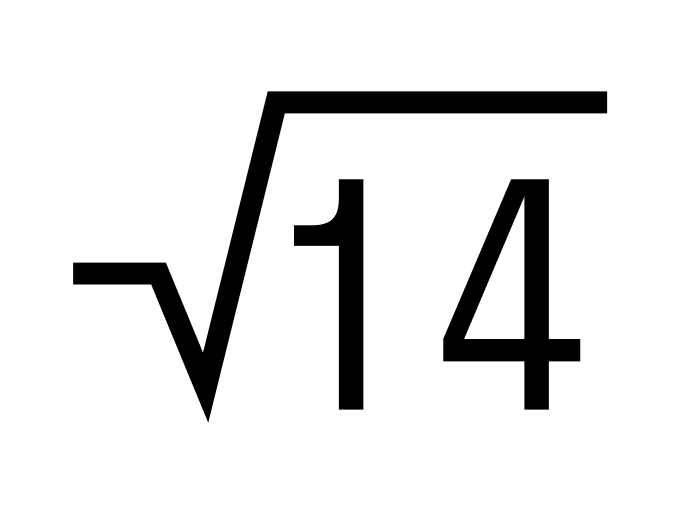
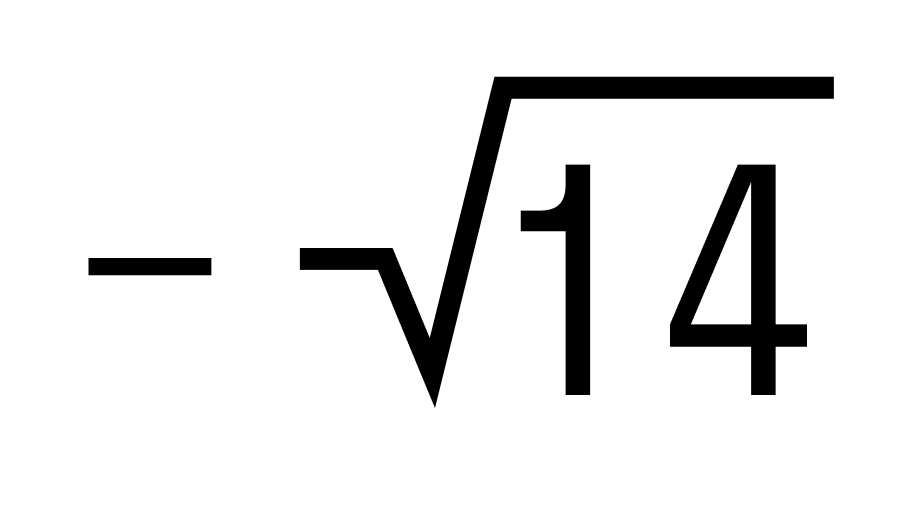
Замечаем, что у складываемых чисел разные знаки, а их модули равны. Значит эти числа являются противоположными, а сумма противоположных чисел равна нулю.
Получается вот так:
Важно помнить, что при сложении действительных чисел с разными знаками результат можно записывать не в виде бесконечной десятичной дроби, а в виде числового выражения, которое содержит корни, степени, логарифмы и прочее.
- Например, результат сложения двух чисел с разными знаками -1 и π записывается так: π — 1.
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Сложение чисел с разными знаками: правило, примеры
В этом материале мы расскажем, как правильно выполнять сложение отрицательного и положительного числа. Сначала мы приведем основное правило такого сложения, а потом покажем, как оно применяется при решении задач.
Видео:Решение систем уравнений методом сложенияСкачать

Основное правило сложения положительных и отрицательных чисел
Мы уже говорили ранее, что положительное число можно рассматривать как доход, а отрицательное – как убыток. Чтобы узнать величину дохода и расхода, надо смотреть на модули этих чисел. Если в итоге окажется, что наши расходы превышают доходы, то после их взаимного учета мы останемся должны, а если наоборот, то мы останемся в плюсе. Если же расходы равны доходам, то у нас будет нулевой остаток.
Используя приведенные выше рассуждения, можно вывести основное правило сложения чисел с разными знаками.
Для сложения положительного числа с отрицательным необходимо найти их модули и выполнить сравнение. Если значения окажутся равны, то мы имеем два слагаемых, которые являются противоположными числами, и их сумма будет нулевой. Если же они не равны, то нам надо учесть, что результат будет иметь тот же знак, что и большее число.
Таким образом, сложение в данном случае сводится к вычитанию из большего числа меньшего. Итог этого действия может быть разным: мы можем получить как положительное, так и отрицательное число. Нулевой результат тоже возможен.
Это правило распространяется на целые, рациональные и действительные числа.
Видео:Решение систем уравнений методом сложенияСкачать

Задачи на сложение положительного числа с отрицательным
Разберем, как применять на практике правило, озвученное выше. Возьмем для начала простой пример.
Вычислите сумму 2 + ( — 5 ) .
Решение
Выполним последовательно шаги, которые мы изучили до этого. Найдем для начала модули исходных чисел, которые будут равны 2 и 5 . Больший модуль – 5 , поэтому запоминаем минус. Далее вычитаем из большего модуля меньший и получаем: 5 − 2 = 3 .
Ответ: ( − 5 ) + 2 = − 3 .
Если в условиях задачи стоят рациональные числа с разными знаками, не являющиеся при этом целыми, то для удобства расчетов нужно представить их в виде десятичных или обыкновенных дробей. Возьмем такую задачу и решим ее.
Вычислите, сколько будет 2 1 8 + ( — 1 , 25 ) .
Решение
Первым делом переведем смешанное число в обыкновенную дробь. Если вы не помните, как это делается, перечитайте соответствующую статью.
Десятичную дробь мы тоже представим в виде обыкновенной: — 1 , 25 = — 125 100 = — 5 4 .
После этого уже можно переходить к вычислению модулей и подсчету результата. Найдем модули: они будут равны 17 8 и 5 4 соответственно. Получившиеся дроби приведем к общему знаменателю и получим 17 8 и 10 8 .
Следующим шагом будет сравнение обыкновенных дробей. Поскольку числитель первой дроби больше, то 17 8 > 10 8 . Если слагаемое со знаком плюс у нас больше, то нам надо запомнить, что результат будет положительным.
Далее вычтем из большего модуля меньший (см. материал о том, как найти разность дробей с одинаковыми знаменателями):
17 8 — 10 8 = 17 — 10 8 = 7 8
Мы уже отмечали ранее, что результат у нас будет со знаком плюс: + 7 8 . Так как плюс писать необязательно, при записи ответа обойдемся без него.
Запишем весь ход решения:
2 1 8 + — 1 , 25 = 17 8 + — 5 4 = 17 8 + — 10 8 = 17 8 — 10 8 = 7 8
Ответ: 2 1 8 + — 1 , 25 = 7 8 .
Найдите, чему будет равна сумма 14 и — 14 .
Решение
Мы имеем два одинаковых слагаемых с разными знаками. Значит, эти числа являются противоположными друг другу, следовательно, их сумма будет равна 0 .
Ответ: 14 + — 14 = 0
В конце статьи добавим, что результат сложения действительных отрицательных чисел с положительными зачастую лучше записывать в виде числового выражения с корнями, степенями или логарифмами, а не в виде бесконечной десятичной дроби. Так, если мы сложим числа n и — 3 , то ответ будет равен n — 3 . Считать окончательный результат нужно далеко не всегда, и можно обойтись приблизительными расчетами. Более подробно об этом мы напишем в статье об основных действиях с действительными числами.
Видео:Сложение и вычитание чисел с разными знакамиСкачать

Сложение и вычитание отрицательных и положительных чисел — правило, формулы и примеры
Впервые знакомство с отрицательными числами происходит в школьном курсе в 6 классе, иногда раньше. Число со знаком «+» называется положительным, противоположное — отрицательным.
Чтобы понять, что такое сложение и вычитание положительных и отрицательных чисел, достаточно воспользоваться координатной прямой. Например, сумма чисел -18 и 2. Сначала отмечаем на координатном отрезке число (-18), откладываем от него вправо, соответствующие масштабу, 2 единичных отрезка, и получаем на координатном луче число -16.
Видео:Сложение и вычитание рациональных и отрицательных рациональных чисел. Практическая часть. 6 класс.Скачать
Правило сложения отрицательных чисел и чисел с разными знаками
Для суммирования двух отрицательных чисел, необходимо:
суммировать их модули;
перед полученной суммой поставить знак «минус».
Например, сложение чисел -9 и -6 будет выглядеть следующим образом:
В данном случае, складываем модули 9 и 6, и перед получившимся натуральным числом 15 ставим знак «-«.
Сложение рациональных или дробных чисел выполняется аналогичным способом:
-26,35 + (-25,35) = -(26,35 + 25,35) = -51,75
К 26,35 прибавляем 25,35 (т. е. мы складываем модули), в итоге получаем 51,75 с отрицательным значением. Перед ним ставим знак «минус».
Для суммирования натуральных чисел со знаками «+» и «-», надо:
из слагаемого с большим значением модуля вычесть слагаемое с меньшим значением;
перед полученным результатом поставить знак того слагаемого, которое имело большее значение.
61,2 + (-31,5) = + (61,2 — 31,5) = 30,5
Модуль большего числа со знаком «+», соответственно, сумма получилась положительная:
-81 + 35 = -(81 — 35) = 46
Большее число со знаком «-», поэтому заменяем плюс на минус и получаем отрицательный ответ.
Видео:Как вычитать дроби с разными знаменателями. #математика #дробиСкачать

Как вычитать отрицательные и положительные числа
Для нахождения разности противоположных чисел, надо к уменьшаемому прибавить вычитаемое с противоположным знаком, то есть заменить разность суммой.
Наглядно данное действие лучше представить в виде формулы:
То есть любое выражение, содержащее знаки сложения и вычитания, следует решать как сумму чисел.
-20 — 14 = -20 + (-14) = -34;
-6,1 + 5,6 = 5,6 + (-6,3) = 0,5.
Разность выражения будет положительной, если уменьшаемое больше вычитаемого, и отрицательной, если значение модуля уменьшаемого меньше вычитаемого. В случае, когда уменьшаемое и вычитаемое одинаковые, их разность будет равна нулю.
15 — 6 = 15 + (-6) = 9 — уменьшаемое 15, больше вычитаемого, поэтому ответ положительный;
-15 — 6 = -15 + (-6) = -21 — уменьшаемое -15, меньше вычитаемого, следовательно, ответ отрицательный.
Если нужно отнять отрицательное число, то два знака «минус» подряд дают знак «плюс».
10 — (-5) = 10 + 5 = 15;
— 10 — (-5) = -10 + 5 = 5 — 10 = -5.
Все вышеперечисленные действия возможно выполнить на калькуляторе. Для этого достаточно ввести сначала модуль числа, потом нажать кнопку изменения знака «+/-».
Например, чтобы задать число -81,73, надо в следующем порядке нажать кнопки: «8», «1», «,», «7». «3», «+/-». А решать пример с отрицательными числами следует в том же порядке, что и с положительными.
Видео:Сложение и вычитание дробей с разными знаменателями.Скачать

Заключение
Для закрепления изученных правил можно использовать различные методы проверки знаний. На первом этапе лучшим вариантом будет тренажер, с помощью которого решение подобных примеров можно довести до автоматизма.
Так же для закрепления материала подойдет тестирование. Его можно провести в виде самостоятельной работы. В конце изучения всех правил применяется контрольная работа, задания для которой можно подобрать из различных дидактических материалов.
🌟 Видео
Сложение чисел с разными знаками | 6 классСкачать

Сложение чисел с разными знаками - математика 6 классСкачать

7 класс, 39 урок, Метод алгебраического сложенияСкачать

Самостоятельная работа: сложение и вычитание положительных и отрицательных целых чисел.Скачать

Сложные уравнения. Как решить сложное уравнение?Скачать

Сложение отрицательных чисел. Сложение чисел с разными знаками.Скачать

Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

6 кл.Сложение чисел с разными знакамиСкачать

Алгебра 8. Урок 3 - Сложение и вычитание дробейСкачать

Сложение чисел с разными знаками | Математика 6 класс #33 | ИнфоурокСкачать


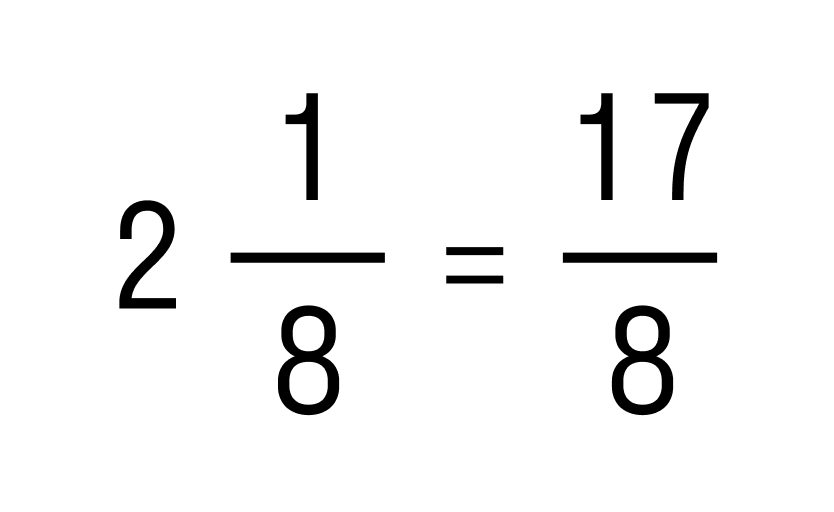 , и переводим десятичную дробь в обыкновенную:
, и переводим десятичную дробь в обыкновенную: 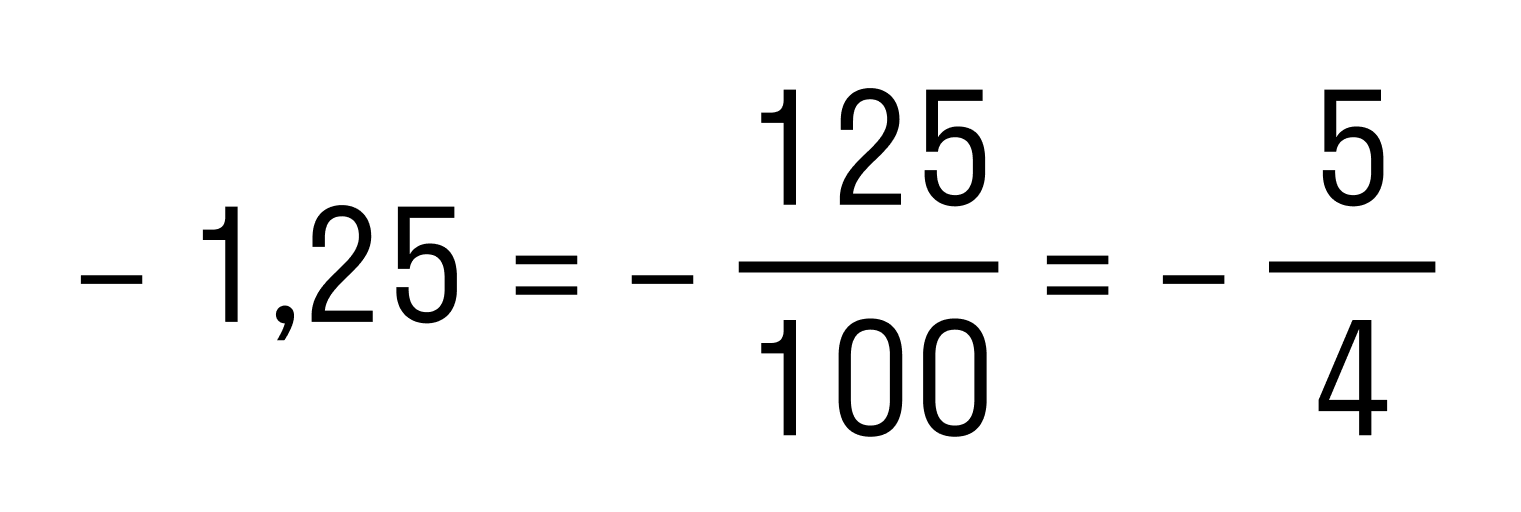
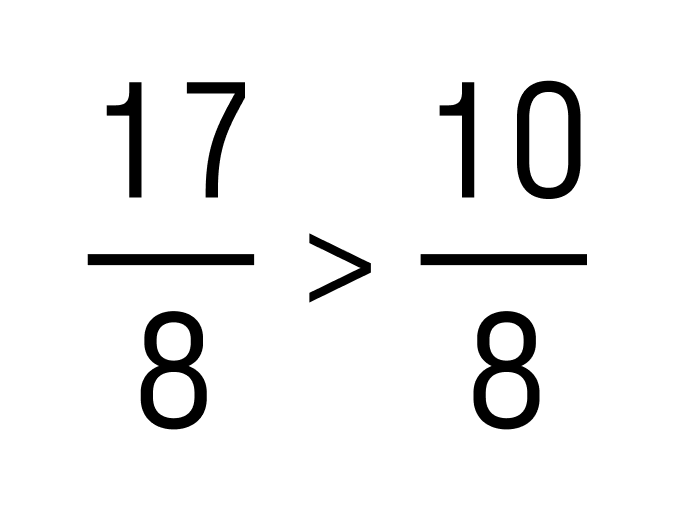 . Это значит, что слагаемое со знаком плюс имеет больший модуль, поэтому запоминаем знак плюс.
. Это значит, что слагаемое со знаком плюс имеет больший модуль, поэтому запоминаем знак плюс.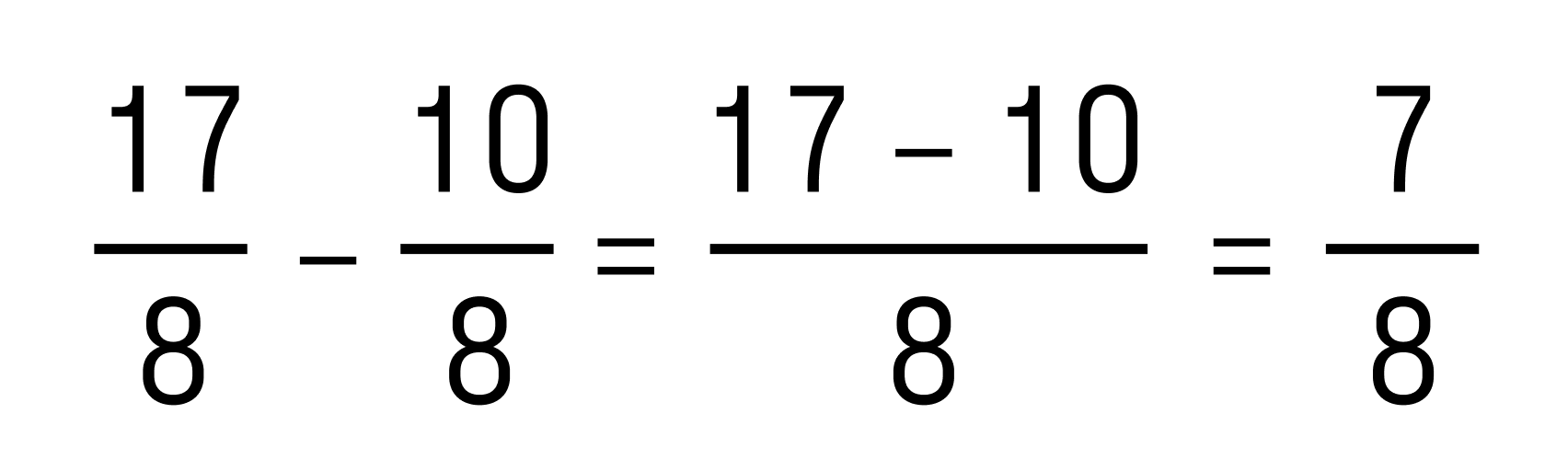
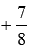 , то есть 7/8.
, то есть 7/8.