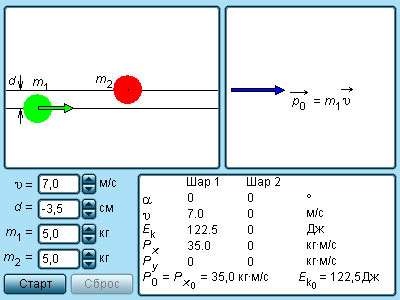
Уравнение скорости второго тела после центрального абсолютно упругого удара двух шаров u2 (8 видео)

Уравнение скорости второго тела после центрального абсолютно упругого удара двух шаров u2

Абсолютно упругий центральный удар

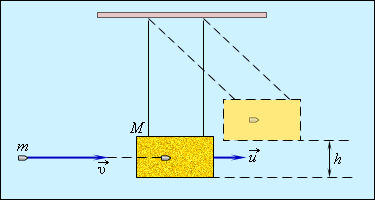
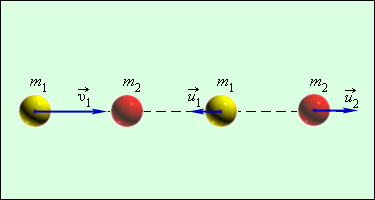
При абсолютно неупругом ударе закон сохранения механической энергии не работает.

Применим закон сохранения механической энергии для расчета скорости тел при абсолютно упругом ударе – ударе, при котором не происходит превращения механической энергии в другие виды энергии.

На рисунке 5.8 изображены два шара m₁ и m₂.

Обозначим и как скорость шаров после их столкновения.

В данном случае можно воспользоваться законом сохранения механической энергии и законом сохранения импульса (в проекциях на ось x):

Решив эту систему уравнений относительно и , получим

Таким образом, скорости шаров после абсолютно упругого удара не могут быть одинаковыми по величине и по направлению.

Рассмотрим теперь абсолютно упругий удар шара о неподвижную массивную стенку. Стенку можно рассматривать как неподвижный шар с υ₂ = 0, массой .

Разделим числитель и знаменатель на m₂ и пренебрежем m₁/m₂ , тогда

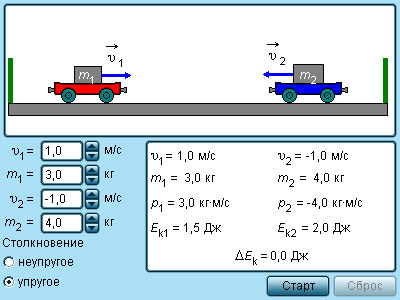
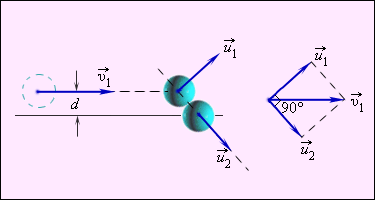
Так, шар m₁ изменит направление скорости на противоположное.

Содержание

§ 6.10. Столкновение упругих шаров
Упругие и неупругие соударения
Абсолютно неупругий удар. Скорость
Абсолютно упругий удар
Предельное расстояние
🎬 Видео

Видео:Урок 128. Соударения телСкачать

§ 6.10. Столкновение упругих шаров

Под абсолютно упругим ударом понимают такой удар, при котором механическая энергия сохраняется(1). Если начальные скорости шаров направлены по линии, соединяющей их центры (рис. 6.22), то удар называют центральным.

Для абсолютно неупругого удара скорости шаров после удара можно найти с помощью закона сохранения импульса (см. гл. 5). При упругом ударе этого закона недостаточно, так как шары после удара будут иметь различные скорости. Значит, нужно еще одно уравнение, которое дает закон сохранения энергии.

Обозначим массы шаров через m₁ и m₂, их скорости до удара через ₁ и ₂, а после удара через ₁ и ₂. Закон сохранения импульса в проекциях на ось X будет иметь следующий вид:

Закон сохранения энергии запишется так:

Нами получена система двух уравнений с двумя неизвестными u_1х и u_2х. Для решения этой системы ее удобно переписать так:

Разделив почленно второе уравнение на первое, получим:

Умножив обе части этого уравнения на m₂ и сложив полученный результат почленно с уравнением (6.10.3), приходим к выражению:

Применив аналогичный прием, получим выражение для проекции скорости ₂:

Применим эти формулы для двух частных случаев.

1. Второй шар до удара покоился (v_2x = 0), тогда

При m₁ > m₂ первый шар продолжает двигаться в том же направлении, что и до удара, но с меньшей скоростью. Если m₁

2. Оба шара имеют одинаковую массу, тогда

Шары при соударении обмениваются скоростями. Проверьте на опыте справедливость этих выводов.

Рассмотрено центральное столкновение абсолютно упругих шаров. Полученные формулы справедливы не только для столкновения макроскопических тел, но и в широких пределах для атомов и элементарных час тиц.

(1) Для этого необходимо, чтобы силы взаимодействия между телами зависели только от деформаций, но не от скоростей их движения друг относительно друга.

Видео:10. Соударение тел. Абсолютно упругий и неупругий ударСкачать

Упругие и неупругие соударения

Закон сохранения механической энергии и закон сохранения импульса при упругом ударе способствует нахождению решения механических задач с неизвестными действующими силами, то есть задания с ударным взаимодействием тел.

Применение такого вида задач используется в технике и физике элементарных частиц.

Удар или столкновение – это кратковременное взаимодействие тел с последующим изменением их скорости.

При столкновении действуют неизвестные кратковременные ударные силы. Закон Ньютона не разрешит ударное взаимодействие, а позволит только исключить сам процесс столкновения и получить связь между скоростями тел до и после столкновений без промежуточных значений.

Механика применяет такое определения абсолютно упругих и абсолютно неупругих ударов.

Видео:Как найти скорость после УПРУГОГО соударения.Скачать

Абсолютно неупругий удар. Скорость

Абсолютно неупругий удар – это ударное взаимодействие с соединением (слипанием) движущихся тел.

Сохранение механической энергии отсутствует, так как переходит во внутреннюю, то есть нагревание.

Попадание пули в баллистический маятник – характерный пример действия энергии абсолютно неупругого удара, где
М – подвешенный ящик с песком, показанный на рисунке 1 . 21 . 1 , m – горизонтально летящая пуля с v → скоростью движения, застревающая в ящике. Определение скорости пули возможно по отклонению маятника.

Если скорость ящика с пулей обозначить как u → , тогда, используя формулу сохранения импульса, получаем:

m v = ( M + m ) u ; u = m M + m v .

Когда пуля застревает в песке, то механическая энергия теряется:

∆ E = m v 2 2 — ( M + m ) u 2 2 = M M + m · m v 2 2 .

M ( M + m ) обозначает долю кинетической энергии выпущенной пули и прошедшей во внутреннюю энергию системы. Тогда

∆ E E 0 = M M + m = 1 1 + m M .

Использование формулы подходит для задач с наличием баллистического маятника и другого неупругого соударения разномасных тел.

Когда m М ∆ E E 0 → 1 2 , тогда происходит переход кинетической энергии во внутреннюю. Когда m = M ∆ E E 0 → 0 , только половина кинетической переходит во внутреннюю. Если имеется неупругое соударение движущегося тела большей массой с неподвижным, имеющим ( m > > М ) , отношение принимает вид ∆ E E 0 → 0 .

Расчет движения маятника производится по закону сохранения механической энергии. Получаем

( M + m ) u 2 2 = ( M + m ) g h ; u 2 = 2 g h .

В данном случае h является максимальной высотой подъема маятника. Отсюда следует, что

v = M + m m 2 g h .

При известной высоте h возможно определение скорости пули v .

Рисунок 1 . 21 . 1 . Баллистический маятник.

Видео:Физика - импульс и закон сохранения импульсаСкачать

Абсолютно упругий удар

Абсолютный упругий удар – это столкновение с сохранением механической энергии системы тел.

Большинство случаев столкновения атомов подчинено законам абсолютного упругого центрального удара. Закон сохранения импульса и механической энергии сохраняются при таком ударе. Для примера используется столкновение при помощи центрального удара бильярдных шаров. Один из них находится в состоянии покоя, как изображено подробно на рисунке 1 . 21 . 2 .

Центральный удар – это соударение, когда скорости шаров направлены по линии центра.

Рисунок 1 . 21 . 2 . Абсолютно упругий центральный удар шаров.

Встречаются случаи, когда массы m 1 и m 2 не равны. Тогда, используя закон сохранения механической энергии, получаем

m 1 v 1 2 2 = m 1 v 1 2 2 + m 2 v 2 2 2 .

За v 1 принимается скорость при абсолютном упругом ударе первого шара перед столкновением, а v 2 = 0 скорость второго шара, u 1 и u 2 – скорости после столкновения.

Запись закона сохранения импульса для проекций скоростей на координатную ось, направленную по скорости движения первого шара до удара, принимает вид:

m 1 v 1 = m 1 u 1 + m 2 u 2 .

Полученная система из двух уравнений позволяет найти неизвестные скорости u 1 и u 2 шаров после столкновения.

u 1 = m 1 — m 2 v 1 m 1 + m 2 ; u 2 = 2 m 1 v 1 m 1 + m 2 .

Если массы равны, то есть, тогда происходит остановка первого шара ( u 1 = 0 ) , а второй продолжает движение u 2 = v 1 _. происходит обмен скоростями и импульсами.

При наличии нулевой скорости второго шара ( v 2 ≠ 0 ) , задача могла бы свестись к предыдущей с переходим в новую систему отсчета с равномерным и прямолинейным движением и скоростью v 2 относительно «неподвижной» системы. В такой системе второй шар покоится до удара, а первый имеет скорость v 1 ‘ = v 1 – v 2 _. После определения скорости шаров v 1 и v 2 производится переход к «неподвижной» системе.

С помощью закона сохранения механической энергии и импульса, можно определить скорости шаров после столкновений только с известными скоростями до соударения.

Рисунок 1 . 21 . 3 . Модель упругие и неупругие соударения.

При столкновении атомов или молекул применяется понятие центрального или лобового удара, который редко применим на практике. Нецентральный упругий удар не направлен по одной прямой.

Частный случай нецентрального упругого удара – соударение бильярдных шаров с одинаковой массой при обездвиженном одним из них, а другим направленным не по линии центра. Данная ситуация приведена на рисунке 1 . 21 . 4 .

Рисунок 1 . 21 . 4 . Нецентральное упругое соударение шаров с одинаковой массой, где d является прицельным расстоянием.

Нецентральное ударение характеризуется тем, что разлетатание шаров происходит под углом относительно друг друга. Чтобы определить скорости v 1 и v 2 после соударения, необходимо знать нахождение положения линии центров в момент удара или предельное расстояние d , изображенное на рисунке 1 . 21 . 4 .

Видео:Удар шаров (абсолютно упругий)Скачать

Предельное расстояние

Предельным расстоянием называют расстояние между двумя линиями, которые проведены через центры шаров параллельно относительно вектора скорости v 1 → летящего шара.

При одинаковых массах шаров векторы v 1 → и v 2 → имеют перпендикулярное направление друг к другу. Это возможно показать с помощью применения законов сохранения импульса и энергии. Если m 1 = m 2 = m , тогда определение примет вид

v 1 → = u 1 → + u 2 → ; v 1 2 = u 1 2 + u 2 2 .

Первое равенство значит, что векторы v 1 → , u 1 → , u 2 → образуют треугольник, называемый диаграммой импульсов, второе – для его разрешения применяют теорему Пифагора. Угол, располагаемый между u 1 → и u 2 → , равняется 90 градусов.