Механика — это раздел физики, изучающий механическое движение тел.
Кинематика — это раздел механики, в котором изучается механическое движение тел без учета причин, вызывающих это движение.
Материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь, если
- расстояние, которое проходит тело, много больше его размера;
- расстояние от данного тела до другого тела много больше его размера;
- тело движется поступательно.
Система отсчета — это тело отсчета, связанная с ним система координат и прибор для измерения времени.
Траектория — это линия, которую описывает тело при своем движении.
Путь — это скалярная величина, равная длине траектории.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением за данный промежуток времени.
Важно!
В процессе движения путь может только увеличиваться, а перемещение как увеличиваться, так и уменьшаться, например, когда тело поворачивает обратно.
При прямолинейном движении в одном направлении путь равен модулю перемещения, а при криволинейном — путь больше перемещения.
Перемещение на замкнутой траектории равно нулю.
Основная задача механики — определить положение тела в пространстве в любой момент времени.
- Механическое движение и его виды
- Относительность механического движения
- Правило сложения перемещений
- Правило сложения скоростей
- Относительная скорость
- Скорость
- Ускорение
- Равномерное движение
- График скорости (проекции скорости)
- График перемещения (проекции перемещения)
- Прямолинейное равноускоренное движение
- Свободное падение (ускорение свободного падения)
- Движение тела по вертикали
- Движение тела, брошенного горизонтально
- Движение тела, брошенного под углом к горизонту (баллистическое движение)
- Движение по окружности с постоянной по модулю скоростью
- Скорость прямолинейного равноускоренного движения. График скорости
- Уравнение движения, графики равномерного прямолинейного движения
- п.1. Прямолинейное равномерное движение на координатной прямой
- п.2. Уравнение прямолинейного равномерного движения
- п.3. Удобная система отсчета для решения задачи о прямолинейном движении
- п.4. График движения x=x(t)
- п.5. Как найти уравнение движения по графику движения?
- п.6. График скорости vx=vx(t)
- п.7. Как найти путь и перемещение по графику скорости?
- п.8. Задачи
- 💥 Видео
Видео:Физика-9. "График проекции скорости"Скачать

Механическое движение и его виды
Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.
Механическое движение может быть:
1. по характеру движения
- поступательным — это движение, при котором все точки тела движутся одинаково и любая прямая, мысленно проведенная в теле, остается параллельна сама себе;
- вращательным — это движение, при котором все точки твердого тела движутся по окружностям, расположенным в параллельных плоскостях;
- колебательным — это движение, которое повторяется в двух взаимно противоположных направлениях;
2. по виду траектории
- прямолинейным — это движение, траектория которого прямая линия;
- криволинейным — это движение, траектория которого кривая линия;
- равномерным — движение, при котором скорость тела с течением времени не изменяется;
- неравномерным — это движение, при котором скорость тела с течением времени изменяется;
- равноускоренным — это движение, при котором скорость тела увеличивается с течением времени на одну и ту же величину;
- равнозамедленным — это движение, при котором скорость тела уменьшается с течением времени на одну и ту же величину.
Видео:Физика - уравнения равноускоренного движенияСкачать

Относительность механического движения
Относительность движения — это зависимость характеристик механического движения от выбора системы отсчета.
Правило сложения перемещений
Перемещение тела относительно неподвижной системы отсчета равно векторной сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной системы отсчета:
где ( S ) — перемещение тела относительно неподвижной системы отсчета;
( S_1 ) — перемещение тела относительно подвижной системы отсчета;
( S_2 ) — перемещение подвижной системы отсчета относительно неподвижной системы отсчета.
Правило сложения скоростей
Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета:
где ( v ) — скорость тела относительно неподвижной системы отсчета;
( v_1 ) — скорость тела относительно подвижной системы отсчета;
( v_2 ) — скорость подвижной системы отсчета относительно неподвижной системы отсчета.
Относительная скорость
Важно! Чтобы определить скорость одного тела относительно другого, надо мысленно остановить то тело, которое мы принимаем за тело отсчета, а к скорости оставшегося тела прибавить скорость остановленного, изменив направление его скорости на противоположное.
Пусть ( v_1 ) — скорость первого тела, а ( v_2 ) — скорость второго тела.
Определим скорость первого тела относительно второго ( v_ ) :
Определим скорость второго тела относительно первого ( v_ ) :
Следует помнить, что траектория движения тела и пройденный путь тоже относительны.
Если скорости направлены перпендикулярно друг к другу, то относительная скорость рассчитывается по теореме Пифагора:
Если скорости направлены под углом ( alpha ) друг к другу, то относительная скорость рассчитывается по теореме косинусов:
Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Скорость
Скорость — это векторная величина, характеризующая изменение перемещения данного тела относительно тела отсчета с течением времени.
Обозначение — ( v ) , единицы измерения — м/с (км/ч).
Средняя скорость — это векторная величина, равная отношению всего перемещения к промежутку времени, за которое это перемещение произошло:
Средняя путевая скорость — это скалярная величина, равная отношению всего пути, пройденного телом, к промежутку времени, за которое этот путь пройден:
Важно! Чтобы определить среднюю скорость на всем участке пути, надо время разделить на отдельные промежутки и все время представить в виде суммы этих промежутков.
Чтобы определить среднюю скорость за все время движения, надо путь разделить на отдельные участки и весь путь представить как сумму этих участков.
Мгновенная скорость — это скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость направлена по касательной к траектории движения.
Видео:§6. Физика 9 кл. Скорость прямолинейного равноускоренного движения. График скорости.Скачать

Ускорение
Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости.
Обозначение — ( a ) , единица измерения — м/с 2 .
В векторном виде:
где ( v ) – конечная скорость; ( v_0 ) – начальная скорость;
( t ) – промежуток времени, за который произошло изменение скорости.
В проекциях на ось ОХ:
где ( a_n ) – нормальное ускорение, ( a_ ) – тангенциальное ускорение.
Тангенциальное ускорение сонаправлено с вектором линейной скорости, а значит, направлено вдоль касательной к кривой:
Нормальное ускорение перпендикулярно направлению вектора линейной скорости, а значит, и касательной к кривой:
Ускорение характеризует быстроту изменения скорости, а скорость – векторная величина, которая имеет модуль (числовое значение) и направление.
Важно!
Тангенциальное ускорение характеризует быстроту изменения модуля скорости. Нормальное ускорение характеризует быстроту изменения направления скорости.
Если ( a_ ) ≠ 0, ( a_n ) = 0, то тело движется по прямой;
если ( a_ ) = 0, ( a_n ) = 0, ( v ) ≠ 0, то тело движется равномерно по прямой;
если ( a_ ) = 0, ( a_n ) ≠ 0, тело движется равномерно по кривой;
если ( a_ ) = 0, ( a_n ) = const, то тело движется равномерно по окружности;
если ( a_ ) ≠ 0, ( a_n ) ≠ 0, то тело движется неравномерно по окружности.
Видео:Расчет ускорения по графикуСкачать
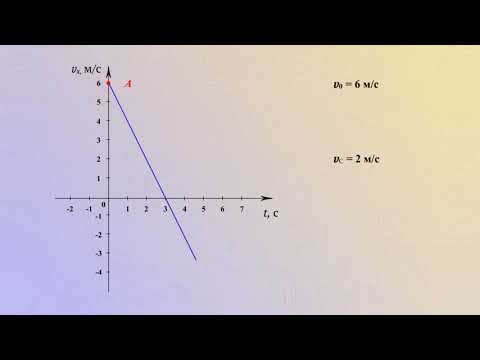
Равномерное движение
Равномерное движение – это движение, при котором тело за любые равные промежутки времени совершает равные перемещения.
Скорость при равномерном движении – величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:
Проекция вектора скорости на ось ОХ:
Проекция вектора скорости на координатную ось равна быстроте изменения данной координаты:
График скорости (проекции скорости)
График скорости (проекции скорости) представляет собой зависимость скорости от времени:
График скорости при равномерном движении – прямая, параллельная оси времени.
График 1 лежит над осью ( t ) , тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ) , тело движется против оси ОХ.
Перемещение при равномерном движении – это величина, равная произведению скорости на время:
Проекция вектора перемещения на ось ОХ:
График перемещения (проекции перемещения)
График перемещения (проекции перемещения) представляет собой зависимость перемещения от времени:
График перемещения при равномерном движении – прямая, выходящая из начала координат.
График 1 лежит над осью ( t ) , тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ) , тело движется против оси ОХ.
По графику зависимости скорости от времени можно определить перемещение, пройденное телом за время ( t ) . Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).
Координата тела при равномерном движении рассчитывается по формуле:
График координаты представляет собой зависимость координаты от времени: ( x=x(t) ) .
График координаты при равномерном движении – прямая.
График 1 направлен вверх, тело движется по направлению оси ОХ:
График 2 параллелен оси ОХ, тело покоится.
График 3 направлен вниз, тело движется против оси ОХ:
Видео:Графики зависимости пути и скорости от времениСкачать

Прямолинейное равноускоренное движение
Прямолинейное равноускоренное движение – это движение по прямой, при котором тело движется с постоянным ускорением:
При движении с ускорением скорость может как увеличиваться, так и уменьшаться.
Скорость тела при равноускоренном движении рассчитывается по формуле:
При разгоне (в проекциях на ось ОХ):
При торможении (в проекциях на ось ОХ):
График ускорения (проекции ускорения) при равноускоренном движении представляет собой зависимость ускорения от времени:
График ускорения при равноускоренном движении – прямая, параллельная оси времени.
График 1 лежит над осью t, тело разгоняется, ( a_x ) > 0.
График 2 лежит под осью t, тело тормозит, ( a_x ) ( v_ ) > 0, ( a_x ) > 0.
График 2 направлен вниз, тело движется равнозамедленно в положительном направлении оси ОХ, ( v_ ) > 0, ( a_x ) ( v_ ) ( a_x ) ( t_2-t_1 ) . Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).
Перемещение при равноускоренном движении рассчитывается по формулам:
Перемещение в ( n ) -ую секунду при равноускоренном движении рассчитывается по формуле:
Координата тела при равноускоренном движении рассчитывается по формуле:
Видео:Скорость прямолинейного равноускоренного движения. График скорости | Физика 9 класс #6 | ИнфоурокСкачать

Свободное падение (ускорение свободного падения)
Свободное падение – это движение тела в безвоздушном пространстве под действием только силы тяжести.
Все тела при свободном падении независимо от массы падают с одинаковым ускорением, называемым ускорением свободного падения.
Ускорение свободного падения всегда направлено к центру Земли (вертикально вниз).
Обозначение – ( g ) , единицы измерения – м/с 2 .
Важно! ( g ) = 9,8 м/с 2 , но при решении задач считается, что ( g ) = 10 м/с 2 .
Движение тела по вертикали
Тело падает вниз, вектор скорости направлен в одну сторону с вектором ускорения свободного падения:
Если тело падает вниз без начальной скорости, то ( v_0 ) = 0.
Время падения рассчитывается по формуле:
Тело брошено вверх:
Если брошенное вверх тело достигло максимальной высоты, то ( v ) = 0.
Время подъема рассчитывается по формуле:
Движение тела, брошенного горизонтально
Движение тела, брошенного горизонтально, можно представить как суперпозицию двух движений:
- равномерного движения по горизонтали со скоростью ( v_0=v_ ) ;
- равноускоренного движения по вертикали с ускорением свободного падения ( g ) и без начальной скорости ( v_=0 ) .
Скорость тела в любой момент времени:
Угол между вектором скорости и осью ОХ:
Движение тела, брошенного под углом к горизонту (баллистическое движение)
Движение тела, брошенного под углом к горизонту, можно представить как суперпозицию двух движений:
- равномерного движения по горизонтали;
- равноускоренного движения по вертикали с ускорением свободного падения.
Скорость тела в любой момент времени:
Угол между вектором скорости и осью ОХ:
Время подъема на максимальную высоту:
Максимальная высота подъема:
Максимальная дальность полета:
Важно!
При движении вверх вертикальная составляющая скорости будет уменьшаться, т. е. тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т. е. тело вдоль вертикальной оси движется равноускоренно.
Скорость ( v_0 ) , с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол ( alpha ) , под которым тело брошено, будет равен углу, под которым оно упадет.
При решении задач на движение тела, брошенного под углом к горизонту, важно помнить, что в точке максимального подъема проекция скорости на ось ОУ равна нулю:
Это облегчает решение задач:
Видео:УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Движение по окружности с постоянной по модулю скоростью
Движение по окружности с постоянной по модулю скоростью – простейший вид криволинейного движения.
Траектория движения – окружность. Вектор скорости направлен по касательной к окружности.
Модуль скорости тела с течением времени не изменяется, а ее направление при движении по окружности в каждой точке изменяется, поэтому движение по окружности – это движение с ускорением.
Ускорение, которое изменяет направление скорости, называется центростремительным.
Центростремительное ускорение направлено по радиусу окружности к ее центру.
Центростремительное ускорение – это ускорение, характеризующее быстроту изменения направления вектора линейной скорости.
Обозначение – ( a_ ) , единицы измерения – м/с 2 .
Движение тела по окружности с постоянной по модулю скоростью является периодическим движением, т. е. его координата повторяется через равные промежутки времени.
Период – это время, за которое тело совершает один полный оборот.
Обозначение – ( T ) , единицы измерения – с.
где ( N ) – количество оборотов, ( t ) – время, за которое эти обороты совершены.
Частота вращения – это число оборотов за единицу времени.
Обозначение – ( nu ) , единицы измерения – с –1 (Гц).
Период и частота – взаимно обратные величины:
Линейная скорость – это скорость, с которой тело движется по окружности.
Обозначение – ( v ) , единицы измерения – м/с.
Линейная скорость направлена по касательной к окружности:
Угловая скорость – это физическая величина, равная отношению угла поворота к времени, за которое поворот произошел.
Обозначение – ( omega ) , единицы измерения – рад/с .
Направление угловой скорости можно определить по правилу правого винта (буравчика).
Если вращательное движение винта совпадает с направлением движения тела по окружности, то поступательное движение винта совпадает с направлением угловой скорости.
Связь различных величин, характеризующих движение по окружности с постоянной по модулю скоростью:
Важно!
При равномерном движении тела по окружности точки, лежащие на радиусе, движутся с одинаковой угловой скоростью, т. к. радиус за одинаковое время поворачивается на одинаковый угол. А вот линейная скорость разных точек радиуса различна в зависимости от того, насколько близко или далеко от центра они располагаются:
Если рассматривать равномерное движение двух сцепленных тел, то в этом случае одинаковыми будут линейные скорости, а угловые скорости тел будут различны в зависимости от радиуса тела:
Когда колесо катится равномерно по дороге, двигаясь относительно нее с линейной скоростью ( v_1 ) , и все точки обода колеса движутся относительно его центра с такой же линейной скоростью ( v_1 ) , то относительно дороги мгновенная скорость разных точек колеса различна.
Мгновенная скорость нижней точки ( (m) ) равна нулю, мгновенная скорость в верхней точке ( (n) ) равна удвоенной скорости ( v_1 ) , мгновенная скорость точки ( (p) ) , лежащей на горизонтальном радиусе, рассчитывается по теореме Пифагора, а мгновенная скорость в любой другой точке ( (c) ) – по теореме косинусов.
Видео:Урок 18 (осн). Координаты тела. График движения. График скоростиСкачать

Скорость прямолинейного равноускоренного движения. График скорости
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
Этот видеоурок посвящен теме «Скорость прямолинейного равноускоренного движения. График скорости». В ходе занятия учащиеся должны будут вспомнить такую физическую величину, как ускорение. Затем они узнают, как определить скорости прямолинейного равноускоренного движения. После учитель расскажет, как правильно строить график скорости.
Видео:Уравнение равномерного прямолинейного движения | Физика 10 класс #3 | ИнфоурокСкачать

Уравнение движения, графики равномерного прямолинейного движения
п.1. Прямолинейное равномерное движение на координатной прямой
Система отсчета, с помощью которой можно описать прямолинейное движение состоит из:
1) тела отсчета; 2) координатной прямой; 3) часов для отсчета времени.
Пусть телом отсчета будет дом.
В начальный момент времени машина стоит в 20 м справа от дома.
Рассмотрим движение машины со скоростью 10 м/с вправо.
Направим координатную прямую параллельно вектору скорости, вправо.
Составим таблицу перемещений за первые 4 секунды:
| t, c | 0 | 1 | 2 | 3 | 4 |
| x, м | 20 | 30 | 40 | 50 | 60 |
Стартуя с точки x0=20, машина каждую секунду удаляется от дома еще на 10 м.
Пройденный путь за 2 секунды – 10·2=20 м, за 3 секунды – 10·3=30 м, за t секунд s=vt метров. Значит, для произвольного времени t можем записать координату x в виде: begin x=x_0+s=x_0+vt\ x=20+10t end
Если при тех же начальных условиях и направлении координатной прямой машина будет двигаться влево, получим таблицу:
| t, c | 0 | 1 | 2 | 3 | 4 |
| x, м | 20 | 10 | 0 | -10 | -20 |
В этом случае координата x в любой момент времени t имеет вид: begin x=x_0-st=x_0-vt\ x=20-10t end Если же машина никуда не едет, её скорость v=0, и координата x=x0 в любой момент времени t.
п.2. Уравнение прямолинейного равномерного движения
Зависимость координаты тела от времени в механике называют уравнением движения.
Если уравнение движения известно, то мы можем решить основную задачу механики.
п.3. Удобная система отсчета для решения задачи о прямолинейном движении
При решении задачи можно выбрать различные тела отсчета и связать с ними различные системы координат. Как правило, некоторая система отсчета является наиболее удобной для решения данной задачи в том смысле, что в ней уравнение движения выглядит и решается проще, чем в других системах.
При решении задач на прямолинейное движение телом отсчета может быть неподвижная поверхность (земля, пол, стол и т.п.), само движущееся тело или другое тело.
При этом системой координат является координатная прямая, параллельная направлению движения (вектору перемещения) тела, уравнение движения которого мы хотим получить.
Проекции скорости и перемещения на координатную прямую могут быть положительными, равными нулю или отрицательными. Величины скорости и перемещения будут равны длинам соответствующих проекций.
п.4. График движения x=x(t)
Сравним полученное уравнение движения (x(t)=x_0+v_x t) с уравнением прямой (y(x)=kx+b) (см. §38 справочника по алгебре для 7 класса).
В уравнении движения роль углового коэффициента (k) играет проекция скорости (v_x), а роль свободного члена (b) – начальная координата (x_0).
 | Построим графики зависимости координаты от времени для нашего примера: |
x=20+10t — машина движется вправо (в направлении оси OX)
x=20-10t — машина движется влево (в направлении, противоположном оси OX)
x=20 — машина стоит
п.5. Как найти уравнение движения по графику движения?
п.6. График скорости vx=vx(t)
Для рассмотренного примера:
п.7. Как найти путь и перемещение по графику скорости?
Пусть тело движется прямолинейно равномерно, зависимость его координаты от времени описывается уравнением: $$ x(t)=x_0+v_x t $$ Тогда в некоторый момент времени (t_1) координата равна (x_1=x_0+v_x t_1).
Несколько позже, в момент времени (t_2gt t_1) координата равна (x_2=x_0+v_x t_2).
Если (v_xgt 0), то пройденный за промежуток времени (triangle t=t_2-t_1) путь равен разности координат: $$ s=x_2-x_1=(x_0+v_x t_2)-(x_0+v_x t_1)=x_0-x_0+v_x (t_2-t_1)=v_x triangle t $$ В общем случае, т.к. (v_x) может быть и отрицательным, а путь всегда положительный, в формуле нужно поставить модуль: $$ s=|v_x|triangle t $$
Изобразим полученное соотношение на графике скорости:
Проекция скорости (v_x) может быть не только положительной, но и отрицательной.
Если учитывать знак, то произведение: $$ triangle x=v_x triangle t $$ дает проекцию перемещения на ось OX. Знак этого произведения указывает на направление перемещения.
Проекция перемещения может быть как положительной, так и отрицательной или равной 0.
п.8. Задачи
Задача 1. Спортсмен бежит по прямолинейному участку дистанции с постоянной скоростью 8 м/с. Примите (x_0=0) и запишите уравнение движения.
а) Постройте график движения (x=x(t)) и найдите с его помощью, сколько пробежит спортсмен за (t_1=5 с), за (t_2=10 с);
б) постройте график скорости (v=v(t)) и найдите с его помощью, какой путь преодолеет спортсмен за промежуток времени (triangle t=t_2-t_1)?
По условию (x_0=0, v_x=8).
Уравнение движения: (x=x_0+v_x t=0+8t=8t)
а) Строим график прямой (x=8t) по двум точкам:
| t | 0 | 5 |
| x | 0 | 40 |
По графику находим: begin x_1=x(5)=8cdot 5=40 text\ x_2=x(10)=8cdot 10=80 text end
б) Скорость (v_x=8) м/с — постоянная величина, её график:
$$ t_1=5 с, t_2=10 с $$ Пройденный путь за промежуток времени (triangle t=t_2-t_1) равен площади заштрихованного прямоугольника: $$ s=v_x triangle t=8cdot (10-5)=40 text $$ Ответ: а) 40 м и 80 м; б) 40 м
Задача 2. Космический корабль движется прямолинейно с постоянной скоростью.
Известно, что через 1 час после старта корабль находился на расстоянии 38 тыс.км от астероида Веста, а через 2 часа после старта – на расстоянии 56 тыс.км.
а) постройте график движения корабля, найдите по графику уравнение движения.
б) на каком расстоянии от астероида находился корабль в начальный момент времени?
в) на каком расстоянии от астероида будет находиться корабль через 4 часа после старта?
г) чему равна скорость корабля в километрах в секунду?
а) Будем откладывать время в часах, а расстояние в тыс.км
Отмечаем точки A(1;38) и B(2;56), проводим через них прямую.
Полученная прямая и есть график движения (x=x(t)).
Найдем скорость корабля (v_x): $$ v_x=frac=frac=18 (text) $$ Найдем начальную координату (x_0): $$ x_0=x_1-v_x t_1=38-18cdot v_1=20 (text) $$ Получаем уравнение движения: $$ x(t)=x_0+v_x t, x(t)=20+18t $$ где (x) – в тыс.км, а (t) – в часах.
б) В начальный момент времени корабль находился на расстоянии (x_0=20) тыс.км от астероида.
в) Через 4 часа после старта корабль будет находиться на расстоянии $$ x(4)=20+18cdot 4=92 (text) $$
г) Переведем скорость в км/с: $$ 18000frac<text><text>=frac<18000 text><1 text>=frac<18000 text><3600 text>=5 text $$ Ответ:
а) (x(t)=20+18t) ((x) в тыс.км, (t) в часах); б) 20 тыс.км; в) 92 тыс.км; г) 5 км/с
💥 Видео
Решение графических задач на равномерное движениеСкачать

Уравнение движенияСкачать

Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

Урок 19 (осн). Задачи на график движенияСкачать
Урок 15. Решение задач на графики движенияСкачать

9 класс, 3 урок, Графики прямолинейного равномерного движенияСкачать

Графическое представление равномерного движения.Скачать

Используя график скорости, составить уравнение движения тела, имеющего начальную координату -10 м.Скачать

Выполнялка 168. Равноускоренное движение. Как строить графики.Скачать

Уравнения и графики механических гармонических колебаний. 11 класс.Скачать




















































































