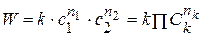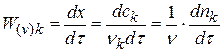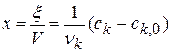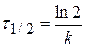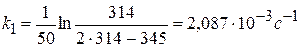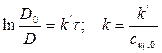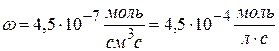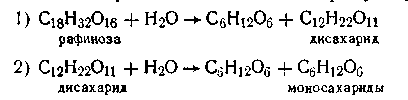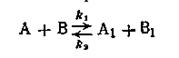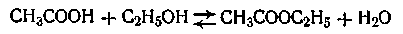ФИЗИЧЕСКАЯ И КОЛЛОИДНАЯ ХИМИЯ
Конспект лекций для студентов биофака ЮФУ (РГУ)
2.1 СКОРОСТЬ ХИМИЧЕСКОЙ РЕАКЦИИ
2.1.1 Кинетическое уравнение химической реакции. Порядок реакции.
Одной из задач, стоящих перед химической кинетикой, является определение состава реакционной смеси (т.е. концентраций всех реагентов) в любой момент времени, для чего необходимо знать зависимость скорости реакции от концентраций. В общем случае, чем больше концентрации реагирующих веществ, тем больше скорость химической реакции. В основе химической кинетики лежит т. н. основной постулат химической кинетики :
Скорость химической реакции прямо пропорциональна произведению концентраций реагирующих веществ, взятых в некоторых степенях.
Т. е. для реакции

Коэффициент пропорциональности k есть константа скорости химической реакции . Константа скорости численно равна скорости реакции при концентрациях всех реагирующих веществ, равных 1 моль/л.
Зависимость скорости реакции от концентраций реагирующих веществ определяется экспериментально и называется кинетическим уравнением химической реакции. Очевидно, что для того, чтобы записать кинетическое уравнение, необходимо экспериментально определить величину константы скорости и показателей степени при концентрациях реагирующих веществ. Показатель степени при концентрации каждого из реагирующих веществ в кинетическом уравнении химической реакции (в уравнении (II.4) соответственно x, y и z) есть частный порядок реакции по данному компоненту. Сумма показателей степени в кинетическом уравнении химической реакции (x + y + z) представляет собой общий порядок реакции . Следует подчеркнуть, что порядок реакции определяется только из экспериментальных данных и не связан со стехиометрическими коэффициентами при реагентах в уравнении реакции. Стехиометрическое уравнение реакции представляет собой уравнение материального баланса и никоим образом не может определять характера протекания этой реакции во времени.
В химической кинетике принято классифицировать реакции по величине общего порядка реакции. Рассмотрим зависимость концентрации реагирующих веществ от времени для необратимых (односторонних) реакций нулевого, первого и второго порядков.
2.1.2 Реакции нулевого порядка
Для реакций нулевого порядка кинетическое уравнение имеет следующий вид:

Скорость реакции нулевого порядка постоянна во времени и не зависит от концентраций реагирующих веществ; это характерно для многих гетерогенных (идущих на поверхности раздела фаз) реакций в том случае, когда скорость диффузии реагентов к поверхности меньше скорости их химического превращения.
2.1.3 Реакции первого порядка
Рассмотрим зависимость от времени концентрации исходного вещества А для случая реакции первого порядка А ––> В. Реакции первого порядка характеризуются кинетическим уравнением вида (II.6). Подставим в него выражение (II.2):


После интегрирования выражения (II.7) получаем:

Константу интегрирования g определим из начальных условий: в момент времени t = 0 концентрация С равна начальной концентрации Со. Отсюда следует, что g = ln Со. Получаем:

Рис. 2.3 Зависимость логарифма концентрации от времени для реакций
первого порядка
Т.о., логарифм концентрации для реакции первого порядка линейно зависит от времени (рис. 2.3) и константа скорости численно равна тангенсу угла наклона прямой к оси времени.

Из уравнения (II.9) легко получить выражение для константы скорости односторонней реакции первого порядка:

Еще одной кинетической характеристикой реакции является период полупревращения t1/2 – время, за которое концентрация исходного вещества уменьшается вдвое по сравнению с исходной. Выразим t1/2 для реакции первого порядка, учитывая, что С = ½Со:


Как видно из полученного выражения, период полупревращения реакции первого порядка не зависит от начальной концентрации исходного вещества.
2.1.4 Реакции второго порядка
Для реакций второго порядка кинетическое уравнение имеет следующий вид:


Рассмотрим простейший случай, когда кинетическое уравнение имеет вид (II.14) или, что то же самое, в уравнении вида (II.15) концентрации исходных веществ одинаковы; уравнение (II.14) в этом случае можно переписать следующим образом:

После разделения переменных и интегрирования получаем:

Постоянную интегрирования g, как и в предыдущем случае, определим из начальных условий. Получим:

Т.о., для реакций второго порядка, имеющих кинетическое уравнение вида (II.14), характерна линейная зависимость обратной концентрации от времени (рис. 2.4) и константа скорости равна тангенсу угла наклона прямой к оси времени:


Рис. 2.4 Зависимость обратной концентрации от времени для реакций
второго порядка
Если начальные концентрации реагирующих веществ Cо,А и Cо,В различны, то константу скорости реакции находят интегрированием уравнения (II.21), в котором CА и CВ – концентрации реагирующих веществ в момент времени t от начала реакции:

В этом случае для константы скорости получаем выражение

Порядок химической реакции есть формально-кинетическое понятие, физический смысл которого для элементарных (одностадийных) реакций заключается в следующем: порядок реакции равен числу одновременно изменяющихся концентраций. В случае элементарных реакций порядок реакции может быть равен сумме коэффициентов в стехиометрическом уравнении реакции; однако в общем случае порядок реакции определяется только из экспериментальных данных и зависит от условий проведения реакции. Рассмотрим в качестве примера элементарную реакцию гидролиза этилового эфира уксусной кислоты (этилацетата), кинетика которой изучается в лабораторном практикуме по физической химии:
Если проводить эту реакцию при близких концентрациях этилацетата и воды, то общий порядок реакции равен двум и кинетическое уравнение имеет следующий вид:

При проведении этой же реакции в условиях большого избытка одного из реагентов (воды или этилацетата) концентрация вещества, находящегося в избытке, практически не изменяется и может быть включена в константу скорости; кинетическое уравнение для двух возможных случаев принимает следующий вид:


2) Избыток этилацетата:


В этих случаях мы имеем дело с т.н. реакцией псевдопервого порядка . Проведение реакции при большом избытке одного из исходных веществ используется для определения частных порядков реакции.
Copyright © С. И. Левченков, 1996 — 2005.
Видео:Задачи на скорость реакции в зависимости от концентрации реагентовСкачать

Тема 2: Реакции первого и второго порядка
НЕРАВНОВЕСНЫЕ ЯВЛЕНИЯ
В СЛОЖНЫХ ХИМИЧЕСИХ ПРОЦЕССАХ
Примеры решения задач
для студентов, обучающихся
по программе бакалавриата по направлению подготовки
240100 – Химическая технология
Тема 1: Кинетика химических реакций.
Реакции первого и второго порядка
Основные расчетные формулы:

Глубина протекания химической реакции
Плотность глубины реакции
Реакция I порядка, интегральное уравнение:

Реакция II порядка: А+В=С

Существует понятие суммарный порядок реакции n = ∑nk и частный порядок реакции по компоненту

Графическое или аналитическое определение Еа

Задача № 1
Термическое разложение в газовой фазе (Т = 849 К, V-const)
происходит как одностадийная реакция. Эта стадия является односторонней, мономолекулярной. Рассчитайте константу скорости прямой реакции по следующим данным:
| τ, с | ∞ |
| р, мм.рт.ст. (общее давление) |
Решение:
1) Для реакции I порядка справедливо интегральное уравнение

k должно быть постоянной.
2) Рассмотрим реакцию
| С2Н5СНО = С2Н6 + СО | |||
| τ = 0 | р0 | х=0 | х=0 |
| τ = τ | р0 – х | х | х |
Р0 – исходное давление С2Н5СНО. В любой момент времени общее давление пара равно


3)
Значение k внесем в таблицу:
| τ, с | ∞ | ||||
| k∙10 3 , с -1 | 2.08 | 1.67 | 1.59 | 1.60 | 1.59 |
4) Вычислим значение kср

Задача № 2
В реакции формальдегида с пероксидом водорода образуется муравьиная кислота (реакция II порядка, 
За время τ = 2 часа при 333,2 К 

Дано:
Реакция II порядка
Решение:
| НСНО + Н2О2 = НСООН + Н2О | ||||
| τ = 0 | с0 = 1 моль/л | с0 = 1 моль/л | 0 моль/л | 0 моль/л |
| τ1 = 2 часа | сτ1 = 0,215 моль/л | сτ1 = 0,215 моль/л | х моль/л | х моль/л |
| τ2 = ? | сτ2 = 0,1 моль/л | сτ2 = 0,1 моль/л | 0,9 моль/л | 0,9 моль/л |
| τ3 = ? | сτ3 = 0,01 моль/л | сτ3 = 0,01 моль/л | 0,09 моль/л | 0,09 моль/л |
Для реакции II порядка при с1,0=с2,0
1) 
2)
3)
Вывод: Если исходные компоненты разбавить в 10 раз, то для достижения той же глубины реакции нужно в 10 раз больше времени.
Задача № 3
Для реакции А→В к = 0,5. Вычислить степень превращения вещества А за время 1 час, если реакция идет по 0, 1 и 2 порядку и с0,1 = 1 моль/л . Определите, как зависит степень превращения вещества от порядка реакции.
Дано:
Решение:
1) Реакция 0 порядка:
2) Реакция 1 порядка:

3) Реакция II порядка

Сведем данные расчета в таблицу:
| Порядок реакции, n | |||
| Степень превращения, α | 0,5 | 0,394 | 0,333 |
Вывод: При одинаковом значении константы скорости реакции с увеличением порядка реакции уменьшается степень превращения вещества.
Задача № 4
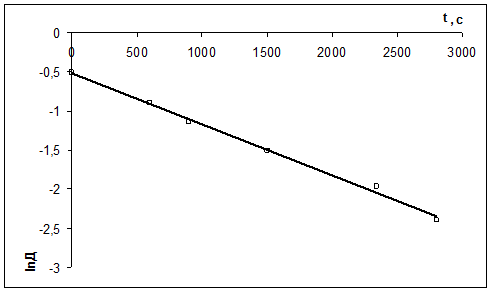
Рассчитать константу скорости реакции кристаллического фиолетового со щелочью по следующим данным
| τ, с | ||||||
| D | 0,600 | 0,405 | 0,320 | 0,220 | 0,140 | 0,091 |
Щелочь берется в избытке: сщ,0 = 1,8 моль/л, скр,0 = 0,01 моль/л, t = 27 0 С.
Решение:
1) Реакция цветная, за концентрацией красителя можно судить по изменению D: D=ε с l

2) Рассчитать k можно графически или аналитическим расчетным способом. Строим график в координатах lnD = f(τ); k ’ = -a = −tgα
| τ, с | ||||||
| lnD | -0,511 | -0,903 | -1,139 | -1,514 | -1,966 | -2,397 |
2)
Задача № 5
Дана реакция 2 порядка А+В=С. Исходные концентрации с0,А = с0,В. За время 500 с реакция проходит на 20%. За какое время она пройдет на 60%?
Решение:
1) Интегральное уравнение реакции II порядка:

Ответ: за 3000 с реакция пройдет на 60%.
Тема 2: Реакции первого и второго порядка
Задача № 1
Рассчитайте k, если скорость реакции II порядка равна 4,5∙10 -7 моль/см 3 ∙с при концентрации одного компонента 1,5∙10 -2 моль/л и другого 2,5∙10 -3 моль/л.
Решение:
Ответ: k = 1,2 л/моль∙с
Задача № 2
Определите возраст мумии, если содержание изотопа углерода 14 С в ее тканях составляет 80% от его содержания в живом организме, а период полураспада 14 С равен 5600 лет. Реакция распада углерода относится к реакциям 1 порядка.
Дано:
Решение:
1) Допустим, что с0 = 1 моль/м 3 , тогда сτ = 0,8 моль/м 3 .
2) Рассчитываем возраст мумии:
Ответ: возраст мумии 1802 года.
Задача № 3
Реакция взаимодействия уксусного ангидрида с водой является реакцией первого порядка
Дано:
Решение:
1) Рассчитываем k:
2)
3)
4)
Вывод: ко времени полупревращения скорость реакции уменьшается в два раза по сравнению с начальным моментом.
Задача № 4
Превращение перекиси водорода в диэтиловый эфир протекает как реакция I порядка. При 333 К за время 10 мин превращение прошло на 75%. Вычислите константу скорости реакции.
Решение:
Допустим, что с0 = 1 моль/л, тогда сτ = с0 – х = 100-75,2 = 24,8%
Задача № 5
Фенилдиазохлорид разлагается по уравнению:
При 323 К и начальной концентрации 10 г/л были получены следующие результаты:
| τ, мин | ∞ | |||
| VN2, cм 3 | 19,3 | 32,6 | 50,4 | 58,3 |
Рассчитайте константу скорости реакции, постойте график VN2 = f(τ) и сделайте вывод о порядке реакции.
Решение:
В данной химической реакции за ходом процесса удобно следить по объему выделившегося газа. Реакция мономолекулярная, скорее всего, протекает согласно реакции I порядка. Кинетическое уравнение для реакции I порядка выглядит так:

Рассчитаем значение константы:
Значения констант скорости реакции имеет почти одинаковые значения, то это реакция I порядка и взятое нами уравнение удовлетворяет или описывает кинетику этого процесса.
Задача № 6
Найдите время, за которое реакция А→В с константой скорости 6,5∙10 -5 с -1 пройдет а) наполовину; б) на 98%.
Решение:
1) по единице измерения константы можно сказать, что данная реакция относится к реакции I порядка.
2) Кинетическое интегральное уравнение можно записать:
При τ = τ1/2 сτ = 0,5с0, если с0 = 1 моль/м 3 , то сτ = 0,5 моль/м 3 .
Видео:Влияние концентрации на скорость химических реакций. 10 класс.Скачать

Лекция № 3 Химическая кинетика
ЛЕКЦИЯ № 3 Химическая кинетика.
Целью исследований химической кинетики является:
1. экспериментальное определение скорости реакции и её зависимости от различных факторов,
2. выявление механизма реакции, т. е. числа стадий и природы образующихся в этих стадиях промежуточных веществ.
Скорость реакции измеряется количеством вещества, реагирующего в единице объёма в единицу времени – (гомогенные реакции) или на единице поверхности раздела фаз (гетерогенные реакции). Отсюда размерности скоростей реакции гомогенной 

Практически скорость гомогенной реакции может быть измерена изменением концентрации исходного вещества или продукта реакции в единицу времени. Этим процессам отвечают диаграммы:
Следует отметить, что даже в самом малом ограниченном участке приведённых кривых скорость реакции непостоянна и, поэтому, истинной скоростью реакции называется скорость в данный момент времени. Она представляет собой первую производную от концентрации по времени
Факторы, влияющие на скорость химических реакций
1. Природа веществ
2. Концентрации веществ (давление — для газофазных реакций)
6. Степень измельчённости – для гетерогенных процессов
Остановимся на некоторых из них.
1. Природа веществ.
С наибольшей скоростью реагируют вещества (неорганические и органические) с ионными, полярными ковалентными связями. Взаимодействия органических веществ с ковалентными малополярными связями протекают значительно медленнее.
2. Концентрация реагентов.
Количественная связь между скоростью и концентрацией реагирующих веществ описывается законом действия масс (, П. Вааге, 1864-1867 г. г.), современная трактовка которого такова: при постоянной температуре скорость реакции прямо пропорциональна произведению концентраций реагирующих веществ, в степенях, равных порядку реакции по этим веществам. Порядок реакции по каждому из реагентов определяют экспериментально.
Для гомогенной реакции
кинетическое уравнение в соответствии с законом действия масс имеет вид

где k – константа скорости реакции, которая численно равна скорости реакции при концентрации каждого из реагентов равной 1 моль/л. Константа скорости характеризует скорость данного процесса при данной температуре; не зависит от концентрации реагентов, зависит от температуры – возрастает с ростом температуры. б и в – порядок реакций по веществам соответственно A и B.
Только для одностадийных реакций, при которых исходные вещества без каких-либо промежуточных соединений превращаются в продукты реакции величины б и в равны стехиометрическим коэффициентам.
Например 

В случае гетерогенных реакций в уравнения закона действия масс вводятся концентрации только веществ, которые находятся в газовой фазе или в растворе. Например, для реакции C(тв) + O2 

Порядок и молекулярность реакции.
Порядок реакции – число, равное сумме показателей степеней концентраций реагентов в кинетическом уравнении.
Порядок реакции может принимать значения от 0 до 3, включая дробные величины.
Для простоты рассмотрим только реакции целочисленного порядка.
Реакции нулевого порядка – такие реакции, скорость которых не зависит от концентрации реагента. Большая часть из них являются гетерогенными реакциями, протекающими на поверхности металла. Например, реакция разложения аммиака на H2 и N2 на поверхности вольфрама является реакцией нулевого порядка, т. е. её скорость на протяжении всего процесса не зависит от концентрации NH3.


Реакции первого порядка
2H2O2 

4AsH3 

Несоответствие между кажущейся молекулярностью и порядком реакции объясняется тем, что в многостадийных реакциях промежуточные превращения осуществляются с несопоставимыми скоростями. Наиболее медленная стадия определяет скорость реализации процесса превращения исходных веществ в конечные продукты. Эта стадия называется лимитирующей.
Например, 2N2O5 
Реакция протекает в две стадии:
N2O5 
N2O5 + N2O3 
Скорость второй бимолекулярной реакции несравненно выше скорости первой – мономолекулярной, следовательно, скорость превращения N2O5 в NO2 определяется первой стадией, чему соответствует уравнение

Важной величиной является время полупревращения (ф1/2) реакции, т. е. время, в течение которого концентрация реагента уменьшается в 2 раза по сравнению с исходным значением. В фармакинетике это обозначается термином “период полуэлиминации”.
Распределение лекарственного препарата, введенного в кровоток, подчиняется кинетике первого порядка.
Подставляя значение 
k1 – константа скорости реакции
Реакции второго порядка – самый распространённый тип реакций. Вот примеры таких реакций
2NO2 
H2 + I2 
CO + Cl2 
2N2O 
Реакции третьего порядка крайне редки.
Исходя из всего вышесказанного, можно определить размерности констант реакций различных порядков.
моль

л

л2 

Под молекулярностью реакции понимают число молекул, которые одновременно взаимодействуют, осуществляя элементарный акт химического превращения. В отличие от порядка реакции молекулярность не может быть ни нулевой, ни дробной.
Мономолекулярные – в элементарном акте химического превращения участвует одна молекула:
н-C4H10 
цикло-C3H6 
Ca(HCO3)2 
Бимолекулярные – реакции, в которых химическое превращение осуществляется путём взаимодействия двух молекул:
CO + Cl2 
H2 + I2 
PH3 + B2H6 
Тримолекулярные реакции – их известно очень немного. Очевидно, что вероятность одновременного соударения трёх молекул в реакционном пространстве очень мала и, поэтому, тримолекулярные реакции идут крайне медленно.
Примеры тримолекулярных реакций:
2NO + O2 
2NO + Cl2 
Реакций более высокой молекулярности не существует.
Влияние температуры на скорость химических реакций упрощённо описывается правилом Вант-Гоффа (1884 г.): при повышении температуры на каждые 10 градусов скорость гомогенной реакции возрастает примерно в 2-4 раза. Математически это правило записывается так:

где 

г – температурный коэффициент Вант-Гоффа
4. Энергия активации.
Более строгую математическую зависимость скорости реакции от температуры описывает уравнение С. Аррениуса (1889 г.), который исходил из предположения, что не всякое столкновение молекул в реакционном объёме заканчивается результативно, т. е. с образованием нового вещества. По С. Аррениусу продукт реакции образуется только при столкновении молекул, обладающих некоторым избытком кинетической энергии, т. е. активных (реакционноспособных) молекул.
ррениуса:
k – константа скорости реакции
A – коэффициент пропорциональности (предэкспоненциальный
множитель), который указывает долю активных молекул
e – основание натурального логарифма; e ≈ 2.718
Ea – энергия активации – избыточная энергия молекул, которой они должны обладать, чтобы их столкновение приводило к химическому взаимодействию
R – универсальная газовая постоянная;
T – абсолютная температура; Т=273 + toC
Наблюдаемые на опыте значения энергии активации находятся в пределах 0 – 400 кДж/моль. Величина Ea может служить критерием скорости протекания химического процесса:
Ea 120 
Первой стадией практически любого химического процесса является образование непрочного промежуточного соединения – активированного комплекса.
Активированный комплекс не является химическим соединением в привычном понимании этого слова. В нём не исчезли первоначально существовавшие в молекулах исходных веществ связи между атомами и не до конца сформировались новые. Однако электронные оболочки атомов во взаимодействующих молекулах определённым образом деформированы в направлении формирования новых химических связей, а прежние связи ослаблены.
Это можно схематично изобразить на примере реакции
H2 + I2 
Образование короткоживущего активированного комплекса требует меньших затрат энергии, чем разрыв связей в молекулах исходных веществ, т. к. этому разрыву содействует взаимное влияние реагентов и наметившееся образование новых связей. В итоге образование непрочного активированного комплекса приводит к уменьшению высоты энергетического активационного барьера.
Особенности каталитических реакций.
а. Катализаторы вводятся в реакцию в очень низких концентрациях.
б. Состав катализатора остаётся неизменным до и после реакции.
в. Катализаторы обладают специфичностью действия, т. е. катализаторы активны по отношению к одним процессам и инертны по отношению к другим. Например:
г. Катализаторы ускоряют как прямую, так и обратную реакции.
д. Катализаторы не влияют на величину константы равновесия, а только ускоряют достижение состояния равновесия.
е. Катализаторы снижают энергию активации.
При введении катализатора в реакционный объём происходят два последовательных процесса – образование промежуточного соединения катализатор–реагент и второй процесс – взаимодействие образованного соединения со вторым реагентом с образованием продукта реакции и освобождением катализатора.
Схематично это можно записать так:
A + B 
A + K 
AK + B 
возвращением катализатора в цикл, Ea3)
Одной из наиболее интересных областей химической кинетики является исследование закономерностей ферментативного катализа. Реакции, катализируемые ферментами, характеризуются высоким ускорением (
Для веществ, участвующих в ферментативных реакциях применимы следующие термины: субстрат (S) – индивидуальное химическое вещество, реакции которого катализируются ферментами (энзимами, E), фермент (E) – каталитически активное вещество, ускоряющее какие-либо превращения субстрата.
Михаэлис и Ментен (1913 г.) установили, что промежуточной стадией практически любой ферментативной реакции является присоединение по месту активных центров фермента молекул субстрата с образованием фермент–субстратного комплекса ES, который распадается с образованием продукта P и освобождением фермента E, чему соответствует схема:
Результатами их исследований стал вывод формулы – уравнения Михаэлиса-Ментен


находится в составе фермент-субстратного комплекса
C(S) – концентрация субстрата
Km – константа Михаэлиса
Уравнение имеет два предельных случая. При низкой концентрации субстрата Km



Графически это выглядит так:
а. первый порядок отн. C(S)
б. нулевой порядок отн. C(S)
Из графика зависимости скорости процесса от концентрации субстрата можно получить также значение Km, т. к. при 

Температурная зависимость скорости ферментативных реакций описывается кривой с максимумом. Восходящая часть кривой отражает обычную для всех химических реакций закономерность. Нисходящая часть показывает снижение активности фермента вследствие тепловой денатурации белковой молекулы, сопровождающейся нарушением её структуры, определяющей активность фермента.
Исследование зависимости скорости ферментативных реакций в температурном интервале, когда не наблюдается тепловой денатурации фермента, даёт возможность оценивать энергетическую характеристику процесса.
Это позволяет сделать общий вывод – высокая каталитическая активность ферментов объясняется как существенным снижением энергии активации, так и значительным благоприятным изменением энтропии в ходе реакции.
Видео:Кинетика || Лекция 4 || Реакции второго порядка, общий интеграл кинетического уравненияСкачать

Реакции второго порядка.
К реакциям второго порядка относятся реакции соединения типа A + B→C, реакции обмена A + B = C + D, а также реакции разложения и др. Скорость реакции второго порядка определяется уравнением
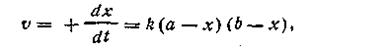 | 2.13 |
где k — константа скорости реакции; а — число молей вещества А в начале реакции; b — число молей вещества В в начале реакции; х—число прореагировавших молей.
Здесь возможны два случая. Первый случай — это когда какое-то количество вещества А вступает в реакцию с эквивалентным количеством вещества В, т. е. когда а = b. И второй случай более сложный — это когда а ≠ b. Рассмотрим оба эти случая.
Первый случай (а= b).Поскольку исходные концентрации реагирующих веществ равны между собой, уравнение (2.13) примет вид
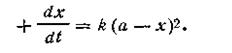 | 2.14 |
Разделяя переменные и производя интегрирование, получим
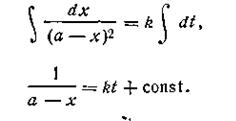 | 2.15 |
При t = 0 x = 0, откуда const =1/а. После подстановки этой величины в уравнение (2.15) получим
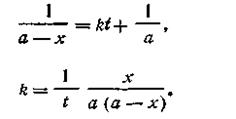 | 2.16 |
Размерность константы скорости реакции второго порядка t -1 C -1 . Поэтому в отличие от константы скорости первого порядка численное значение k зависит от того, в каких единицах выражены t и С. Если последняя выражена в кмоль/м 3 , а время в с, то k имеет размерность [с -1 ·(кмоль/м 3 ) -1 ].
Для реакций второго порядка большую роль играет число столкновений, которые происходят в единицу времени между молекулами реагирующих веществ. Число столкновений, в свою очередь, пропорционально числу молекул в единице объема, т. е. концентрации. Таким образом, константа скорости, а следовательно, и скорость реакции второго порядка зависят от разбавления раствора.
Второй случай (а ≠ b). Если для реакции взяты неэквивалентные количества реагирующих веществ, скорость реакции выразится так:
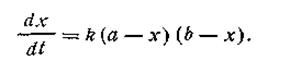 | 2.17 |
После разделения переменных получим это уравнение в другом виде:
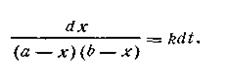 | 2.18 |
Выражение, стоящее в левой части уравнения (2.18), можно представить как
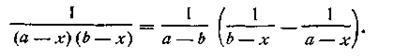 | 2.19 |
Поcле подстановки этого выражения в уравнение (2.13) получим
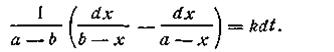 | 2.20 |
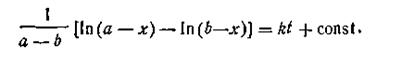 | 2.21 |
Поскольку при t = 0 х = 0, постоянная интегрирования
 | 2.22 |
Подставляя это выражение в уравнение (2.16), найдем
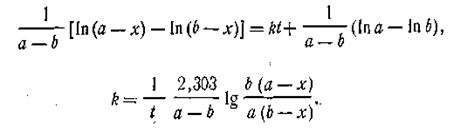 | 2.23 |
Это и есть кинетическое уравнение реакции второго порядка. Примером подобной реакции может служить омыление эфиров щелочами:
Кинетика реакций второго порядка была детально изучена С. Г. Крапивиным еще в 1915 г.
Реакции третьего порядка встречаются очень редко и потому не имеет смысла рассматривать математический вывод их кинетического уравнения.
Существуют экспериментальные способы определения порядка реакции, основные из них:
подстановки в кинетическое уравнение реакций,
определение полупериода реакций,
Сложные реакции.
Сложными называются реакции, общее кинетическое уравнение которых в отличие от кинетического уравнения простых реакций содержит несколько констант скоростей. К сложным реакциям относятся обратимые, параллельные, последовательные, сопряженные, цепные и другие реакции. Теория всех этих реакций основана на положении, что при протекании в системе одновременно нескольких реакций каждая из них проходит самостоятельно и к каждой из них в отдельности применимы уравнения кинетики простых реакций.
Параллельными реакциями называются реакции вида
т. е. при которых одни и те же исходные вещества, одновременно реагируя, образуют разные продукты. Примером подобного типа реакций является реакция разложения бертолетовой соли КСlO3, которая может идти в двух направлениях:
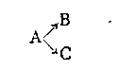
Примером последовательных реакций может служить гидролиз рафинозы трисахарида, который происходит через стадии образования дисахарида, а последний образует уже моносахариды:
Расчет кинетики последовательных реакций в общем виде очень сложен и здесь не рассматривается. Отметим только, что если одна из ступеней обладает значительно меньшей скоростью, чем остальные, то общая скорость реакции определяется скоростью именно этой ступени.
Сопряженными реакциями называются реакции, которые протекают по следующей схеме:
Реакция 1 может протекать самостоятельно, в то время как реакция 2 проходит при наличии реакции 1. Так, сульфат железа окисляется пероксидом водорода независимо от присутствия йодистого водорода. Последний же в чистом виде пероксидом водорода не окисляется, но при окислении сульфата железа окисляется одновременно с ним.
Обратимыми называются такие реакции, скорость которых равна разности между скоростями прямой и обратной реакции:
Примером обратимой реакции, может служить реакция образования сложного эфира
В этом случае скорость прямой реакции с течением времени убывает, а скорость обратной реакции возрастает до тех пор, пока обе скорости не выравняются и не наступит так называемое состояние динамического равновесия. Константа равновесия данной реакции равна отношению констант скоростей прямой и обратной реакции.
Наряду с рассмотренными выше реакциями, механизм которых сравнительно прост, существуют также реакции, в которых взаимодействие осуществляется более сложным путем. Примером подобных реакций являются цепные реакции, которые имеют исключительно большое значение в химической технологии, так как на них основаны такие процессы, как полимеризация, крекинг нефти, деление атомного ядра.
К цепным реакциям относится большая группа реакций, протекающих путем образования цепи следующих друг за другом реакций, в которых участвуют активные частицы с ненасыщенными свободными валентностями — так называемые свободные радикалы. Свободные радикалы образуются за счет дополнительного поглощения энергии при разрыве связей в молекуле, при электрическом разряде, при поглощении электромагнитных колебаний, а также за счет других внешних источников энергии.
Сущность цепного механизма реакции заключается в том, что активная молекула, реагируя, порождает новую активную молекулу или реакционноспособную частицу (валентно-ненасыщенные свободные атомы или радикалы). Процесс исчезновения и регенерации каждой активной частицы в дальнейшем циклически повторяется много раз и создает цепь превращений, совершающихся частью последовательно, а частью параллельно.
Впервые определение цепного механизма реакций через образование активных центров было дано Н. А. Шиловым (1904). Чрезвычайно большой вклад в дело изучения цепных реакций внес Н. Н. Семенов, которому за эти исследования была присуждена Нобелевская премия.
В настоящее время цепные реакции изучены настолько хорошо, что стало осуществимо регулирование скорости этих реакций. Добавляя вещество, легко вступающее во взаимодействие с активными центрами, можно значительно увеличить число обрывов цепей и тем самым затормозить (или же прекратить вовсе) цепную реакцию.
Например, добавление всего лишь 0,01% NС1з (треххлористого азота) к смеси водорода и хлора (Н2 и С2), которые реагируют по типу цепных нарастающих реакций, уменьшает скорость образования хлористого водорода в десятки тысяч раз.
Некоторые добавки увеличивают скорость цепных реакций. Так, добавление сравнительно малых количеств N0 в значительной степени ускоряет цепные реакции окисления углеводородов. При этом удается значительно понизить температуру процесса окисления, что очень важно, так как сохраняются от сгорания ценные промежуточные продукты — уксусный и муравьиный альдегиды.
На цепных химических реакциях основаны многие технологические процессы — синтез спиртов, кетонов, формалина, уксусной кислоты.
В последнее время исследования показали, что некоторые биологические процессы также протекают по типу цепных реакций, в частности процессы биологического окисления.
📺 Видео
Расчет скорости химической реакции по текущим концентрациям реагентов. Химия для поступающих.Скачать

Вычисление константы скорости реакции | Задачник по химии ГлинкаСкачать

Занятие 4. "Энергетический профиль химической реакции".Скачать
Урок 152. Среднеквадратичная скорость молекул. Опыт ШтернаСкачать

Реакции типа Е2Скачать

Скорость химических реакций. Гомогенные и гетерогенные реакции. Химия 8 классСкачать

Обработка результатов измерений. 2. Характеристики погрешностейСкачать

Скорость химической реакции. Гомо- и гетерогенные реакции. Механизм реакции.Скачать

Расчет средней скорости химической реакции. Химия для поступающих. Разбор задач.Скачать

Моделирование прогнозных сейсмических воздействий, расчет акселерограмм и спектров реакцииСкачать

Лекция 6. Скорость химической реакцииСкачать

Решение систем Д/У: 2. Опции решателей odeXYСкачать

Объёмный анализ ( титрование)Скачать

Механизмы химических реакций. Ч.2. Классификация механизмов. Электрофильные и нуклеофильные реакции.Скачать

09 Фаз диагр двухкомп сист 1 принципы и мех смесьСкачать
Дискретный анализ 2. Унициклические графыСкачать

В системе А(г) + В(г) ↔ 2С(г) через 300 секунд концентрации веществ A и С установились соответственнСкачать