Б3.Б.5 ГЕОДЕЗИЯ
Б3.Б.2 ГЕОДЕЗИЯ
Практическое занятие.
Уравнивание системы нивелирных и теодолитных ходов
Направление: 120700 Землеустройство и кадастры
120100 Геодезия и дистанционное зондирование
Рекомендовано к изданию методической комиссией факультета землеустройства и лесного хозяйства (протокол № 1 от 03. 09. 2012 г.)
Составители: доцент Ишбулатов М.Г., ст. преп. Яковлева Ю.Н.
Рецензент: доцент, к.т.н. Лемешев А.И.
Ответственный за выпуск: заведующий кафедрой кадастра
недвижимости и геодезии, к.с-х..н., доцент Ишбулатов М.Г.,
г. Уфа, БГАУ, кафедра кадастра недвижимости и геодезии
Общие сведения
Съемочная сеть, делится на плановую и высотную.
Плановая высотная сет в зарыто местности строится в виде отдельных теодолитных ходов или систем теодолитных ходов, опирающихся на пункты исходной геодезической сети, а также в виде свободных сетей теодолитных полигонов.
Высотная геодезическая сеть строится методом геометрического или тригонометрического нивелирования. Она может состоять из отдельных нивелирных ходов или систем нивелирных ходов, опирающихся на пункты исходной высотной сети более высокого класса, а также в виде сетей свободных полигонов.
При уравновешивании несвободных съемочных сетей координаты или отметки пунктов исходной сети должны быть известны, при этом они рассматриваются как безошибочные и не подлежат исправлению. Поэтому такие пункты часто называют твердыми.
Рассмотрим уравновешивание свободных и несвободных сетей ходов. Для этих сетей существуют различные способы уравновешивания.
Уравнивание системы нивелирных ходов с одной узловой точки
Требуется уравновесить систему нивелирных ходов с одной узловой точки по рисунку 1, опирающуюся на пункты нивелирования ранее построенной сети более высокого класса, если известны: отметки исходных пунктов На, Нв, Нд, суммы измеренных превышений по ходам h1 h2, h3, длина ходов L1 L2,L3.
Рисунок 1 Схема нивелирных ходов
Составляется схема ходов, и вычисляются невязки с суммой превышений по наиболее коротким ходам. Для определения достоверности вычисляют допустимую невязку по формуле 2.1..
где Z — длина хода (км).
Определяется отметка узловой точки по каждому ходу.
Для нивелирного хода определяется вес.
Средне весовое значение отметки определяется формулой 2.2.

где
Вычисляются невязки превышений по каждому ходу.
Полученные невязки распределяются на превышения соответствующих
ходов и определяются отметки точек.
Производится оценка точностей полевых работ, определяется средняя квадратическая погрешность единицы веса по формуле 2.3.

где N — количество ходов
Средняя квадратическая погрешность определения узловой точки определяется по формуле 2.4.

3 Уравнивание теодолитных ходов с одной узловой точки
Требуется уравнять систему теодолитных ходов с одной узловой точкой, опирающихся на пункты и стороны ранее построенной сети более высокого класса (рисунок 2), если известны: координаты пункты В, Д, F и дирекционные углы сторон АВ, СД, ЕF исходной сети и измеренные значения углов и длин теодолитных ходов уравниваемой системы.
Теодолитные хода уравновешивают упрощенно: вначале уравновешивают углы, затем вычисляют приращения координат, которые уравновешивают, условно считая их независимыми. Такой способ называют способом раздельного уравнивания.
Рисунок 2 Схема теодолитных ходов
Узловая сторона 2-3. Для этой линии находим значения дирекционных углов каждого хода по формуле 3.1.
где исходной формулой будет формула 3.2
По найденным значениям α находят угловые невязки по формулам 3.3, по ходам заключенными между исходными дирекционными углами, выбираем два хода с наименьшим числом углов.
Если полученные невязки оказываются допустимыми, то определяют вес каждого направления на основании формулы 3.4
где n– количество углов, k = const.
По формуле 3.5 вычисляют средне весовое значение дирекционного угла узловой линии.
α = 

Вычисление невязок, по ходам 1, 2, 3 по формуле 3.6
Σ β теор = (для разомкнутого хода) = α нач + 180 ° ·n – α кон
f βi = α – ( αi исх + 180 ° ·n – Σ βi исх ) или f βi = α – αi
f βi = α – αi – если в формуле применялись измеренные правые по ходу углы
f βi = αi – α – если в формуле применялись измеренные левые по ходу углы
Контролем правильности вычисления дирекционного угла α и невязки fβi является формула: [ p f β] = 0
Если невязки являются допустимыми, их распределяют с противоположным знаком в соответствующие ходы (поровну на каждый угол).
Вычисляют дирекционные углы всех сторон.
Средняя квадратическая ошибка измеренного угла определяется по формуле 3.7:
m = 
Средне квадратическая ошибка единицы веса определяется формулой 3.8:
μ = 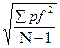
где N– число ходов.
При малом количестве числа ходов оценка точности является грубой.
По вычисленным дирекционным углам и длинам сторон вычисляют приращение координат и их суммы по ходам. Уравнивание приращений координат производится, так же как и уравнивание углов.
Для проверки правильности линейных измерений вычисляют невязки, по двум наиболее коротким ходам.
Если невязка допустима, вычисляют веса, для каждого значения координат узловой точки.
у= 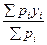
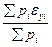

По этим координатам вычисляют невязки приращения по каждому ходу
Правильность вычисления окончательных координат узловой точки и невязку приращения координат, определяется по формуле:
[ p f x ] = 0; [ p f у ] = 0
Полученные невязки с противоположным знаком распределяются на приращения соответствующих ходов, пропорционально длинам этих ходов. После распределения невязок вычисляют координаты всех вершин теодолитных ходов.
Таблица 1 Варианты уравнивания нивелирной сети с одной узловой точкой
| Вариант | Реперы | Превышения | Расстояния | |||||
| Pn 10 | Pn ll | Pn l2 | h 1 | h 2 | h 3 | L 1 | L 2 | L 3 |
| 101,242 | 151,278 | 136,539 | 28,111 | -21,921 | -7,182 | 3,9 | 4,4 | 4,2 |
| 139,567 | 125,872 | 137,939 | -10,182 | 3,599 | -8,554 | 3,7 | 4,2 | 4,3 |
| 123,829 | 132,534 | 121,765 | 5,519 | -3,142 | 7,638 | 4,0 | 4,1 | 4,2 |
| 117,678 | 129,975 | 102,761 | -1,795 | -14,065 | 13,121 | 3,1 | 3,9 | 3,6 |
| 126,721 | 101,975 | 103,761 | -10,839 | 13,909 | 12,122 | 3,8 | 4,1 | 3,7 |
| 135,562 | 115,782 | 112,781 | -13,782 | 5,997 | 8,997 | 3,7 | 1,0 | 4,1 |
| 129,781 | 134,642 | 102,698 | -8,007 | -12,891 | 19,052 | 3,9 | 4,2 | 4,1 |
| 101,597 | 136,246 | 145,756 | 20,149 | -14,471 | -23,980 | 4,1 | 4,0 | |
| 159,761 | 161,523 | 127,693 | -17,421 | -19,182 | 14,678 | 3,8 | 4,3 | 4,2 |
| 160,843 | 131,372 | 126,593 | -18,497 | 10,971 | 15,748 | 3,6 | 3,9 | 3,5 |
| 25,92 | 27,861 | 32,676 | 4,669 | 2,721 | -2,095 | 3,2 | 4,1 | 3,6 |
| 28,21 | 31,672 | 54.925 | 2,489 | -1,062 | -4,235 | 3,5 | 4,2 | 3,3 |
| 34,26 | 32,821 | 28,563 | -4,142 | -2,239 | 2,018 | 3,8 | 4,0 | 4,1 |
| 58,263 | 62,973 | 52,821 | -1,468 | -6,198 | 3,981 | 4,0 | 3,9 | 3,9 |
| 66,627 | 59,947 | 51,088 | -3,838 | -3,145 | 5,719 | 3,7 | 4,1 | 3,3 |
| 51,623 | 46,264 | 41,889 | -5,921 | -0,581 | 3,812 | 3,4 | 3,9 | 4,1 |
| 40,005 | 43,580 | 50,989 | 5,695 | 2.115 | -5,312 | 3,6 | 3,2 | 3,8 |
| 151,621 | 124,735 | 132,534 | -11,050 | 15,830 | 8,032 | 2,8 | 3,1 | 2,7 |
| 79,777 | 65,621 | 64,328 | -7,650 | 1 6,505 | 7,810 | 3,2 | 2,9 | 3,6 |
| 98,126 | 102,435 | 105,272 | 14,340 | 10,035 | 7,200 | 2,5 | 3,0 | 3,2 |
| 103,626 | 107,534 | 112,439 | -3,630 | -7,542 | -12,450 | 3,1 | 3,2 | 3,7 |
| 83,555 | 94,121 | 80,666 | 12,340 | 1,772 | 15,226 | 3,1 | 3,5 | 2,6 |
| 41,333 | 43,222 | 50,721 | 8,560 | 6,672 | -0,837 | 3,2 | 3,7 | 3.1 |
| 54,768 | 56,852 | 59,747 | 5,680 | 3,590 | 0,697 | 4,2 | 3,8 | 2,6 |
| 99,999 | 100,500 | 87,645 | -10,005 | -10,510 | 2,350 | 3,6 | 3,7 | 3,8 |
| 74,688 | 82,539 | 76,561 | 10,320 | 2,460 | 8,448 | 3,9 | 2,1 | 3,7 |
| 80,532 | 85,679 | 73,468 | 1,460 | -3,685 | 8,530 | 3,4 | 3,3 | 2,6 |
| 120,571 | 130,232 | 122,643 | 4,436 | -5,230 | 2,366 | 3,4 | 2,8 | 3,6 |
| 40,263 | 37,563 | 48,711 | -6,036 | 15,123 | 2,418 | 3,2 | 4,1 | 2,9 |
| 70,325 | 62,888 | 60,222 | 4,470 | 2.972 | +5,628 | 5,1 | 4,2 | 4,3 |
| 81,232 | 71,242 | 80,335 | -3,082 | 6,000 | -3,981 | 4,8 | 5,2 | 3,9 |
| 38,262 | 44,356 | 46,555 | -4,637 | -2,428 | 3,666 | 3,8 | 2,6 | 2,5 |
| 41,444 | 49,566 | 40,838 | 3,956 | -4,780 | 3,336 | 6,4 | 5,2 | 4.3 |
1. Маслов А.В. и др. Геодезия. – М.: Недра, 1980. – 528 с.
2. Баканова В.В. и др. Практикум по геодезии. – М.: Недра, 1983.– 240 с.
3. Шестюков А.Д., Баканова А.И. Справочное пособие по геодезическим работам при возведении гидротехнических сооружений. М.: Недра,
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Способы уравнивания теодолитных ходов.
С пособы уравнивания теодолитных ходов постоянного съемочного обоснования на настольных клавишных машинах
В зависимости от сложности системы теодолитных ходов их уравнивают как одиночный ход или как систему с одной узловой точкой, либо как систему ходов.
При уравнивании теодолитных ходов применяют способ эквивалентной замены (проф. А. С. Чеботарева); способ узлов или способ полигонов (проф. В. В. Попова) или метод наименьших квадратов. Опытом и расчетами установлено, что в сетях с незначительным числом пунктов и в сетях простых по своей конструкции, уравнительные вычисления выгодно вести средствами обычной вычислительной современной техники. Сложные и громоздкие сети надо уравнивать строгим методом наименьших квадратов с использованием ЭВМ, который имеет неоспоримое преимущество перед приближенными способами.
Перед уравниванием теодолитных ходов необходимо проверить журналы измерения углов и сторон теодолитного хода и нанести
па их значение схему (рис. 7.6).
На схеме условными знаками показывают точки поворота проложенных теодолитных ходов (поворотные, створные и висячие), и все пункты полигонометрии, имеющиеся на данной территории углы наклоны сторон хода к горизонту, а также данные компарнрования мерных приборов или определенный коэффициент дальномера. Обработку угловых и линейных измерений теодолитных ходов начинают с заполнения ведомости вычислений ^значениями измеренных горизонтальных углов правых или левых по ходу, а не их дополнения, и сторон хода.
7.4.1. Вычисление одиночного теодолитного хода (см. рис. 7.6). Пример вычисления приведен в табл. 7.10.
Пол ученная»! в этом ходе угловая невязка /(1 сопоставляется с допусти-
Если при вторичном контроле угловая невязка осталась недопустимой, то выполняют контрольные измерения углов хода независимо от первых измерений, обращая особое внимание на центрировку теодолита и вех.
Полученную угловую невязку в теодолитном ходе, если она допустима, распределяют с обратным знаком на все его углы поровну, после чего вычисляют дирекционные углы по формуле:
при левых углах хода а„+1 = а„ + р—180°; (7.15)
при правых углах хода а„+1 —а„+180°—р. (7.16)
Контролем является получение дирекционного угла линии, к которой привязан ход. В противном случае допущена ошибка, и тогда сначала следует проверить вычисление дирекционных углов, а затем правильность найденной невязки и поправок в утлы.
После определения углов вычисляют приращения координат. При вычислении приращения координат на счетах пользуются таблицами [1 ], а при вычислении на счетах, счетных машинах, арифмометрах и калькуляторах пользуются таблицами [41].
Приращения вычисляют до сантиметров, а знаки определяют в зависимости от дирекционных углов, как показано в табл. 7.11.
После получения приращений подсчитывают отдельно сумму приращений по оси х и по оси у, а также длину хода.
Здесь следует сличить полученную с допустимой длиной хода, не превышающей 800 м, предусмотренной Инструкцией СП 212—73.
Невязки в приращениях координат определяют по каждой оси по формулам:
/*= 2 Ах— (Л’кон —*нач); (7.17)
ftJ — 2 Дг/—(г/кон—-z/нач) (7.18)
и вычисляют абсолютную fs и относительную Fs невязки по формулам
Относительная невязка Fs не должна быть более —5— L, а абсо-
лютная — не более 0,25 м; длина хода L не должна превышать 800 м.
Если невязка fs меньше или удовлетворяет указанному допуску, то невязки fx и fy распределяются на каждое приращение пропорционально длине стороны хода по формулам:
где бxi и бtji — поправки соответственно в приращения координат х и у.
Если в теодолитном ходе невязка в дирекционном угле окажется выше допустимой, тогда следует полагать, что ошибочно измерены несколько длин сторон или углов.
Уравнивание системы теодолитных ходов с одной узловой точкой. При уравнивании системы теодолитных ходов часто применяют способ эквивалентной замены (проф. А. С. Чеботарева). Идея способа заключается в том, что ряд ходов системы с несколькими узловыми точками заменяется одним эквивалентным ходом, в результате чего получается один одиночный ход, эквивалентный всей системе. После того как составлена и проверена схема теодолитных ходов, ходы нумеруют по порядку и выписывают в ведомость. Так, для системы теодолитных ходов с одной узловой точкой ходы нумеруют с таким расчетом, чтобы последний ход имел наибольшую длину. В пашем случае это будет ход от узловой точки 15 к триангуляционному пункту «Новая» (рис. 7.7). Вначале подсчитывают эквивалент двух ходов z-y и z2 (табл. 7.12) по определению дирекцион-ного угла направления Шпиль башни — 15.
Для первого хода с числом углов 3 находят дирекциоиный угол, равный 30Г19,5′ с весом 1/3 = 0,33; для второго хода, имеющего
4 угла, получают дирекциоиный угол 301°16,4′ весом—-—^=0,25 ;
за приближенное значение принимают дирекциоиный угол 301°15,0′ и подсчитывают рАа, где р — вес дирекционного угла, а Да — уклонение от приближенного значения. Соответственно получают р Дах = 0,33 X 4,5 = 1,5 и рАаг = 0,25 X 1,4 = 0,35; дирекциоиный угол, полученный по ходу, эквивалентному ходам zt и гъ который обозначают через z1/2, имеет п + 1 углов, получаемых по формуле (л + 1)1-г =-—-= 1,7 и определяется
Рис. 7.7. Схема системы теодолитных ходов с одной узловой точкой
К этому ходу Zi. 2 присоединяют ход z3, имеющий 5 углов, а следовательно, одиночный ход, эквивалентный всей данной системе ходов, имеет 6,7 углов. Угловая невязка данного эквивалентного хода будет равна /„ = 30Г18,2’—30Г19.0′ = -0,8′, которая, естественно, должна распределяться на 6,7 углов поровну. Для хода z3 поправка равна — 0,6, а для хода Zi. 2 = + 0,2. Таким образом, уравненный дирекционный угол получают дважды: ЗОГ’18,2′ + 0,2 = 301 °18,4′ по ходу г1л и 301°19,0’—0,6 = 30Г18.4′ по ходу z3. Теперь уже можно определить невязки по ходам гъ как 301°19,5’—30Г18.4′ = + 1,1′ и z2 = 30Г16.4’—301°18,4′ = = — 2,0′, которые распределяются поровну соответственно на три и четыре узла.
В результате данная система распадается на ряд самостоятельных одиночных ходов, имеющих определенные угловые невязки; остается только сравнить их с допустимыми, которые указываются в ведомости вычислений (см. табл. 7.12). Уравнивать можно также методом узлов и методом полигонов, разработанными проф. В. В. Поповым. Применяя метод узлов для уравнивания полигона, приведенного на рис. 7.7, выписывают полученные по каждому ходу дирекционные углы узловой стороны и число углов, с помощью которых был получен этот дирекционный угол. Затем вычисляют
веса этого дирекционного угла по формуле после чего
вычисляют величины отклонений от приближенного, произвольно взятого угла (в табл. 7.12 этот дирекционный угол равен 121°19,0′) и затем определяют окончательный дирекционный угол стороны 15 — Шпиль башни как среднее по формуле
_„ Д«х/>1 + Aaa/?g+ А«зРз п on
«•15—шпиль башни—»‘от i j >
как показано в табл. 7.13.
В случае метода полигонов составляют нормальные уравнения. Для полигона г2, г3 и полигона гг, z3; в них ход z3 — общий. Получают уравнения
3£а + 5 (k2—ki)— 0,5 = 0; 8^—5^—0,5’= 0.
Эти уравнения решают по схеме Гаусса (см. табл. 7.14) и получают поправки в углы для каждого хода.
К двум последним методам следует обращаться в крайнем случае, когда применение эквивалентной замены затруднительно. Теперь, после распределения невязок поровну на каждый угол, вы-
Название хода
Дирекционный угол хода
Число узлов
Все р
12|°19,5′ 121 16,4 121 19.0
0,333 0,250 0,200
+0,5 —2,6 0
+0.167 —0.650 0,000
+ 1,1 —2,0 +0,6
+0,37 —0,50 +0,12
4-0,41 + 1,00 +0,07
а 1б— шпиль башни
121°I8,?83′
in —- +.0,97=0,84 Vl.27 б„= [P Aa l ^ °» 183 =—0.617; a=I21°I9,0′ — 0,617’=I2I’18,383′: a IP] 783
m= 1/ ^ a l = j- 0,74 — + o,86; где /«„ — потребность дирекинонного угла,
б^ — поправка к принятому дирекциовному углу, т — средняя квадратическая погрешность измеренного угла, R — число ходов, равное 3, a q — число узлов, равное 1.
Поправки
Контроль
ход г,
3 (0,372) =+1,1
[tol=(+0,496x—2,6)+ +
+0.2Я9 +0,207 +0,496
—0,2889 —0,5 + 1,444
ход г2 ход г3
5 (0,124)=0,6
[/да]— (—2,6х—0,2889) + + (—1,944 X -6.372)=0.751 + +0,723=1,474
числяют дирекционные углы, по сходимости последнего дирекцион-иого угла с определенным ранее убеждаются, что они вычислены верно (см. табл. 7.12).
Далее заполняют графу «длин сторон», в которую вписывают горизонтальные проложения (т. е. стороны, исправленные за компарирование, за превышения (углы наклона) и температуру, если последняя отличается па величину более от температуры компарнрования), после чего вычисляют приращения. При вычислении рекомендуется пользоваться полученными дирекциоииыми углами, а не румбами, так как это ведет к дополнительным вычислениям и, как следствие, к возможным ошибкам.
Во избежание многих ошибок практика вычислительных работ показала, что всегда следует стремиться к тому, чтобы вычитание заменить сложением. Так, для определения приращения Ах по ди-рекциоииому углу а в пределах 90—180° или 270—370°, например,
cos 125°15,3′ = — sin (120 с 15,3′ + 100° + 10 ;; ) — —sin 35°15,3′; sin 125=15,3’= + cos35°15,3′; cos317 18,2′ = = -I-sin (317 а 18,2′ — 300° +30°)= + sin 4748,2′; sin 317° 18,2′ = —cos4?°i8,2′,
Эти равенства могут быть определены мнемоническим правилом: для нахождения приращений Ах и Д у по заданному дирекцион-ному углу а необходимо прибавить к числу десятков дирекцион-ного угла столько единиц, сколько сотен в заданном дирекционном угле а, а остальные цифровые величины оставить без изменения. При прибавлении нечетных единиц Дх определяется по синусу, а Ду — по косинусу; при четном числе — наоборот.
По получении приращений подсчитывают координаты узловой точки и периметр хода до узловой точки. Порядок вычислений остается прежний, а именно: имея координаты, полученные по
определяют вероятнейшее значение координат узловой точки по формулам Pi + Pi) Pi + Pi
где xa и t/o — приближенное значение координат узловой точки.
Рекомендуется за х0 и у0 принимать координаты, полученные по одному из ходов с наименьшим их значением.
Пользуясь суммой весов рг + р2, определяют длину хода, им эквивалентного. Так, для данного примера рх + Рг = 5,21 (см. табл. 7.13), чему соответствует эквивалентный ход длиной 192 м. Прибавляя длину хода z3, получают эквивалентный ход, периметр которого равен 759 м, т. е. система хода сведена к одиночному ходу.
Так как длина всего хода оказалась меньше 800 м — максимальной длины, предусмотренной инструкцией СП 212—73, то следует продолжить уравнивание этого хода, т. е. определить невязку хода путем сравнения координат, получая их по ходу z3 и ходу 21i2. Невязка в эквивалентном ходе но оси х, равна + 1 см, и по оси у — 19 см.
Распределяя невязку пропорционально длинам ходов, получают поправки для хода z3, равными соответственно — 1 и — 14 см и для хода Z],о равными 0 и — 5 см, которые определяют окончательные координаты узловой точки, а именно — 404,21 и + 437,08. Распределив пропорционально длинам сторон полученную поправку с обратным знаком, определяют координаты промежуточных точек в каждом ходе. Контролем служат координаты узловой точки, вычисления которых по каждому ходу должны дать одну и ту же величину.
Следует также произвести оценку точности каждого хода, подсчитывая как абсолютную погрешность fs = 1 /11+ fy , так и относительную Fs = которые не должны превышать предель ной величины, а относительная Fs не может быть более 1 : 2000.
В рассмотренной системе с одной узловой точкой 15 можно подсчитать, как это делалось для углов, погрешность определения координат узловой точки. Она получится /„ = ± 4,8 см и fy = = ± 5,8 см, Д = ± 7,5 см (табл. 7.15).
Таблица 7.15
Назпапне хода
Периметр хода, км
Вес Р
— 18,348
— 18,348
—21,510
—24,654
Z l . 2. 3
а /з ЭТ * = 15,4 см
погрешность координат узловой fx — ‘2,8:^/0,143 — ± 4,8 см;
fy = 15,4 VoTT43 = ± 5,8 см.
7.4.3. Уравнивание с и с т е м ы теодолитных ходов с тремя узловыми точка м и. По схеме (рис. 7.8) намечают порядок уравнивания, для чего подсчитывают длину эквивалентного хода, имеющего непосредственную связь по крайней мере с двумя твердыми пунктами, т. е. подсчитывают эквивалент ходов zJ и z2, ze и z-i и получают эквивалентные ходы соответственно длиной 248 и 290 м; учитывая длину примыкающих ходов г:1 и zr„ находят эквивалентные ходы длиной 666 и 662 м, что меньше длины хода z7.
Таким образом, следуя указаниям, изложенным при уравнивании системы ходов с одной узловой точкой, следует наметить такой порядок уравнивания: узловая точка 103, потом 107 и, наконец, 110 (табл. 7.16).
Приступая к уравниванию, подсчитывают дирекционные углы узловой линии 103 — Громоотвод, получаемые по ходам zx и z2; определяют число углов п, необходимых для вычисления дирек-
Рис. 7.8. Схема системы теодолитных ходов с тремя узловыми точками
ционного угла; находят веса по формуле р — — и получают эк вивалентный дирекциоиный угол Zi. 2 (в нашем примере 49°09,0′, графа 2 табл. 7.17); определяют сумму весов 0,50 (графы 3 и 4), прибавляя к полученному эквивалентному дирекционному углу сумму углов по ходу z2, находим дирекциоиный угол линии 107 — Угол дома, полученный по ходу zT. 2 + z3, равный 141°44,9′ и имеющий 4 угла (по эквиваленту zL.2 2 угла и по ходу z3 3, графа 2, строки 3 и 4).
Определяя точно таким же образом дирекциоиный угол этой линии по ходу находим эквивалентный дирекциоиный угол, заменяющий ходы zu z2, z3 и zx, обозначая это определение символом Zi.2.3.4, по весам определяем дирекциоиный угол (в нашем примере 141°45,7′) с числом углов 1,9.
Прибавляя к нему углы по ходу z5, находим дирекциоиный угол линии 110— Колокольня по ходам Zi.2.3.4-h z5 и zG, получим 76°58,3′ и 76°56,0′. Так же определяем эквивалентный дирекциоиный угол ходов zu z2, z3, z4, z5 и z0, равный 76°56,9′, и, сравнивая его с ди-рекционным углом, полученным по ходу z7 (76°54,Г), определяем невязку эквивалентного хода уравниваемой системы, состоящей всего из 2,4 -+- 4,0 = 6,4- угла. Распределяя полученную невязку (в нашем случае + 2,8) на все углы поровну, найдем окончательный дирекциоиный угол линии 110 — Колокольня, равный 76°54,1′ + 1,8′ или 76°56,9′ — 1,0′ = 76°55,9′.
Так как по ходу Zj.2.3.4 -j- zr> получен дирекциоиный угол 76°58,3′, а окончательный получен 76°55,9′, то имеем поправку, равную — 2,4, которая должна быть распределена на 5,9 угла, и, таким образом, ход Zi.2.з.4 должен получить поправку — 0,8′, и ход z-a — поправку 1,6′ (графа 5 табл. 7.17).
Подобным же образом поступают и с дирекционным углом линии 107 — Угол дома. Так, он определился как 6°18,6’—0,8′, а следовательно, ход z4 должен получить поправку — 1,3′, а ход Zj.2 + г3 поправку 0,0. Это говорит о том, что окончательный дирекциоиный угол линии 103 — Громоотвод будет равен 42°09,0′ и поправки дирекционных углов ходов zx и z2 будут соответственно + 1,1′ и — 1,Г (графа 5).
После распределения угловых невязок по ходам и вычисления дирекционных углов всех линий системы находят приращения Дх и А у и определяют их суммы по ходам отдельно для Дх и Д у.
Определяют координаты х и у точки 103 по ходам гг и z2 и находят среднее весовое ее значение х12 = 8,572 и у12 — 9,469, принимая за вес величину, обратную длине хода (в приведенном примере [sx] = 607 м и = —— = 1,64; fs2] = 419 м и р2 = — 1 — =
=,2,39. По сумме весов (4,03, графа 9) определяют периметр эквивалентного хода, равен он 248 м. К нему прибавляют длину 418 м хода zо, получают длину хода Z].2 + z3 равную 666 м, а также координаты точки 107 : х = 9,892 м и у — 4,269 м. Затем по ходу z4 находят координаты этой же точки х = 9,82 м и у = 4,20 м, берут весовое среднее и находят х = 9,841 м и у — 4,221 м; прибавляют сумму приращений по ходу z5 получают координаты точки 110 : х = 0,381 м у = 9,721 м с длиной 200 + 372 м. Одновременно вычисляют координаты точки 110 по ходу z8 : х = 0,41 м и у — 9,80 м с периметром 448 м, берут весовое из ходов Z.2.3.4 + z5 и zc, получают координаты по ходу г1ЛшЗА.ЬЛ : х = 0,396 м и у = =9,764 м (графы 6 и 7 табл. 7.17) и периметр 262 м; сравнивая эти координаты с координатами по ходу z-,, получают невязки fx = = + 0,096 м и /,, = •+ 0,114 м, которые относят к эквивалентному ходу всей системы длиной 972 м.
Распределяя пропорционально длинам ходов невязки fx и fy (см. табл. 7.16), найдем окончательное значение координат точки 110 : х = 0,370 ми у = 9,733 м, а отсюда и иевязки по ходам:
Видео:Системы уравнений. Способ уравнивания коэффициентов - 1Скачать

Практикум по геодезии (стр. 7 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
В случае разомкнутого теодолитного хода его вычислительная обработка такая же, как и замкнутого хода, кроме следующих вычислений: угловую невязку для правых по ходу измеренных углов находят по формуле
¦b =åbизм — [ aн — aк +180 °´ n],
где [ aн — aк +180 °´ n] — теоретическое значение суммы измеренных углов;
aн — дирекционный угол исходной (начальной) стороны хода;
aк — дирекционный угол конечной стороны хода.
Для левых по ходу углов невязку находят по формуле
¦b =åbизм — [ aк — aн +180 °´ n].
Невязка в приращения координат определяется следующим образом:
где хк, ук — координаты конечного пункта теодолитного хода;
хн, ун — координаты начального пункта теодолитного хода.
Все остальные вычисления производятся так же, как и в замкнутом теодолитном ходе.
В некоторых случаях теодолитные ходы между пунктами опорной геодезической сети прокладываются в виде систем ходов с узловыми точками. Их уравнивание имеет свои особенности.
Например, теодолитные ходы, проложенные между опорными пунктами А, В и С (рис. 3.6) с координатами ХА, УА; ХВ, УВ; ХС,, УС и исходными дирекционными углами a1, a2, a3, образуют узловую точку М с прилегающими к ней узловыми линиями.
Рис. 3.6. Схема системы теодолитных ходов с одной узловой точкой
По каждому ходу известна сумма измеренных углов åbi. Уравнивание начинается с определения дирекционных углов выбранной, например, узловой линии MN по каждому из трех ходов:
aMN1 =a1 +åb1 — 180°´ n1;
aMN2 =a2 +åb2 — 180°´ n2;
aMN3 =a3 +åb3 — 180°´ n3,
где n1- число измеренных левых по ходу углов в первом ходе; n2 — число измеренных левых по ходу углов во втором ходе; n3 — число измеренных правых по ходу углов в третьем ходе.
Разности вычисленных дирекционных углов (aMN1 — aMN2) и (aMN2 — aMN3) не должны превышать допустимых невязок
Затем вычисляется вероятнейшее значение дирекционного угла узловой линии MN по формуле

В качестве веса рi принимают величины, обратные числу углов в ходах, т. е.
Вычисления удобно выполнять в таблице, форма которой представлена в табл. 3.9.
Таблица вычисления вероятнейшего значения дирекционного угла узловой линии
a узловой линии
¦b1 = -1,3¢; ¦b доп = ±2,6¢
¦b2 = +0,1¢; ¦b доп = ±2,4¢
¦b3 = +0,5¢; ¦b доп = ±2,2¢
Угловые невязки для ходов вычисляют по формулам
Полученные невязки распределяют поровну в измеренные углы с обратным знаком и по исправленным углам вычисляют окончательные дирекционные углы всех линий каждого теодолитного хода.
Затем вычисляют приращения координат по каждому ходу и координаты узловой точки М:
Вероятнейшее значение координат узловой точки М может быть получено по формулам


Здесь в качестве веса pi принимают величины, обратные длинам теодолитных ходов pi = 1 / Di. Вычисления можно представить в виде табл. 3.10.
Таблица вычисления вероятнейших значений координат узловой точки
Длины ходов Di, км
После вычисления вероятнейших значений координат узловой точки М по каждому ходу вычисляют невязки ¦Х и ¦У в приращениях координат
которые распределяют прямо пропорционально длинам линий. По исправленным значениям приращений координат вычисляют координаты всех точек теодолитных ходов. Контроль вычислений при этом такой же, как и при уравнивании одиночного теодолитного хода.
В ряде случаев для сгущения съемочного обоснования координаты отдельных точек целесообразно определять способом геодезических засечек, таких, как прямая и обратная угловые, комбинированная засечки, а в случае использования электронных дальномеров — линейная. В некоторых случаях используется способ снесения координат с вершины знака на землю.
3.4.1. Прямая угловая засечка
Задача прямой угловой засечки состоит в определении координат третьей точки по координатам двух исходных пунктов (однократная засечка). Для контроля правильности вычисления координат определяемого пункта необходимо выполнить измерения еще с одного исходного пункта (многократная засечка). Однократная засечка позволяет произвести контроль вычислений координат определяемой точки, а многократная — контроль измерений. Возможны различные схемы и формулы решения задачи прямой угловой засечки.
1. Если между исходными пунктами имеется прямая видимость, то с них измеряются горизонтальные углы bi между смежными направлениями на определяемую точку. Углы засечки должны быть не менее 30° и не более 150°. Схема засечки показана на рис. 3.7.
Рис. 3.7. Схема многократной прямой угловой засечки
При выполнении вычислительных работ необходимо оцифровать пункты и углы по следующему правилу: если вы находитесь на линии базиса АВ против определяемой точки Р, то левый исходный пункт будет первым с координатами X1, У1 и измеряемый при нем угол b1, правый — вторым с координатами Х2, У2 и измеряемый при нем угол b2, а определяемый пункт — третьим с координатами ХР, УР. В этом случае для вычисления координат определяемого пункта удобнее всего воспользоваться формулами котангенсов внутренних углов треугольника (формулами Юнга):


2. Если между исходными пунктами нет прямой видимости (рис. 3.8), то измеряются углы b1 и b2 соответственно на исходных пунктах А и В, а для контроля правильности определения координат пункта Р — угол b3 на пункте С между направлениями на определяемую точку и направлениями на другие исходные пункты, на которые имеется видимость.
Рис. 3.8. Схема многократной прямой угловой засечки
В этом случае наиболее удобными для вычислений являются формулы Гаусса (тангенсов и котангенсов дирекционных углов), в которые входят дирекционные углы направлений с исходных пунктов на определяемый угол ai. Два дирекционных угла a1 и a2 нужны для решения задачи, а третий — для контроля правильности определения пункта Р и повышения точности окончательных значений его координат. Формулы тангенсов дирекционных углов имеют следующий вид:

Формулы котангенсов дирекционных углов выглядят так:

Пользуясь измеренными углами b1 и b2 с исходных пунктов на определяемую точку, вычисляют дирекционные углы a1 и a2, которые могут изменяться от 0° да 360°.
Формулами тангенсов нельзя пользоваться, если дирекционные углы a1 и a2 близки к 90° или 270° и находятся в пределах 90 ± 15°, 270 ± 15°, т. к. в этих пределах функция тангенса имеет значительные колебания при изменении углов на 1¢ и они тем больше, чем ближе к 90° или 270°.
📺 Видео
После этого видео, ТЫ РЕШИШЬ ЛЮБУЮ Систему Нелинейных УравненийСкачать

Решение систем уравнений методом подстановкиСкачать

Решение системы уравнений методом ГауссаСкачать

Способы решения систем нелинейных уравнений. 9 класс.Скачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Метод узловых и контурных уравненийСкачать

ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать

Система уравнений. Метод алгебраического сложенияСкачать

Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

9 класс, 11 урок, Методы решения систем уравненийСкачать

Решение систем уравнений. Методом подстановки. Выразить YСкачать

Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

9 класс, 6 урок, Уравнение окружностиСкачать

Однородное уравнение в системеСкачать

Системы уравнений Тема3 С истемы ур-й в которых одно ур-е 1ой степени а другие 2ой и более высокой.Скачать

Линейное уравнение с одной переменной. 6 класс.Скачать


















