Уравнение упругой волны — это зависимость от координат и времени скалярных или векторных величин, характеризующих колебания среды при похождении в ней рассматриваемой волны. При распространении в упругой среде механических возмущений, возбуждаемых источником волн, происходит перенос энергии, поэтому такие волны называют бегущими волнами.
Упругая волна называется синусоидальной или гармонической, если соответствующие ей колебания частиц среды являются гармоническими.
Геометрическое место точек, в которых фаза колебаний имеет одно и то же значение, называется волновой поверхностью. Волна называется плоской, если ее волновые поверхности представляют совокупность плоскостей, параллельных друг другу.
Уравнение плоской волны, распространяющейся вдоль оси ОХ в непоглощающей среде, можно записать в виде:
Здесь s — величина, характеризующая колебательное движение среды; и — скорость распространения волны. Колебания в некоторой точке отличаются от колебаний в начале координат (О) сдвигом по времени
Уравнение плоской синусоидальной волны, распространяющейся в непоглощающей среде вдоль положительного направления оси ОХ, имеет вид:
Здесь А — амплитуда волны; со = —— циклическая частота волны,
Т — период колебаний; ср0 — начальная фаза колебаний в точках координатной плоскости х = 0; (р = ( + ср0) — фаза плоской волны.
Расстояние X = х>Т, на которое распространяется синусоидальная волна за время, равное периоду колебаний, называется длиной волны. Длина волны X равна расстоянию между двумя ближайшими точками среды, для которых разность фаз колебаний равна 2л.
Еще одна характеристика синусоидальной волны — волновое число к, которое численно равно количеству длин волн, укладывающихся на отрезке длиной 2л.
Уравнение плоской синусоидальной волны (4.3.2) можно также записать в виде:
Волновым вектором называется вектор к, по модулю равный волновому числу к и направленный вдоль луча в рассматриваемой точке. Лучом называется линия, касательная к которой в каждой ее точке совпадает с направлением распространения волны, т. е. с направлением переноса энергии волной.
Волновой вектор плоской синусоидальной волны не зависит от выбора точки. Для плоской синусоидальной волны, распространяющейся вдоль положительного направления оси ОХ, выражение (4.3.4) можно записать в виде:
Здесь к — ki, кх = кг, где г — радиус-вектор, определяющий положение равновесия колеблющейся точки среды.
Волна называется сферической, если ее волновые поверхности имеют вид концентрических сфер; такие волны возбуждаются в однородной изотропной среде уединенным точечным источником. Центр этих сфер называется центром волны.
Для синусоидальной сферической волны запишем:
где А(г) — амплитуда волны; ср0 — начальная фаза колебаний в центре волны.
Можно доказать, что при распространении сферической волны в непоглощающей среде амплитуда волны удовлетворяет соотношению:

где а0 — физическая величина, численно равна амплитуде волны на расстоянии г = 1 м от центра волны.
В линейной однородной, изотропной, непоглощающей среде волны описываются дифференциальным уравнением в частных производных, которое называется волновым уравнением и имеет вид:
Скорость v распространения синусоидальной волны называется фазовой скоростью. Эта скорость равна скорости перемещения в пространстве точек поверхности, соответствующей любому фиксированному значению фазы синусоидальной волны.
Например, для случая плоской синусоидальной волны, задавая фиксированное значение фазы волны, cot — кх + ср0 = const, найдем производную от координаты по времени, т. е. скорость:
Можно получить, что скорость продольной волны в однородной газообразной среде определяется выражением:
где р — плотность газа (р = const), К — модуль объемной упругости газа.
Скорость поперечных упругих волн в неограниченной изотропной твердой среде
Здесь G — модуль сдвига среды, р — плотность среды.
Распространение продольных волн в тонком стержне связано с его продольным растяжением и сжатием. Для скорости продольных волн в тонком стержне можно получить, используя модуль Юнга Е для материала стержня,
Скорость распространения поперечных волн в натянутой тонкой нити (в струне) зависит от натяжения струны и определяется выражением:
где F — сила натяжения струны; р — плотность материала струны; Sceч — площадь ее поперечного сечения.
Заметим, что упругие свойства и плотность твердых тел и жидкостей зависят от химического состава и мало изменяются при различных давлениях и температурах.
Приближенно можно считать, что скорость упругих волн в твердых телах и в жидкостях постоянна.
Модуль объемной упругости К газа зависит от вида термодинамического процесса его объемной деформации, поэтому скорость упругих волн в идеальном газе зависит от частоты волн (дисперсия волн). Колебания частиц среды при распространении в ней упругих волн совершаются с той же частотой, что и колебания источника волн.
Будем считать, что при очень быстрой деформации, т. е. при достаточно большой частоте колебаний частиц среды (газа), реализуется адиабатический процесс.
Тогда можно получить выражение для скорости упругих волн в идеальном газе при адиабатическом процессе.
где у — показатель адиабаты; R — универсальная газовая постоянная, Т — температура, М- молярная масса.
Из опытов скорость слышимых звуковых волн в газах слабо зависит от частоты и может определиться выражением (4.3.9), если плотность газов не велика.
- Если уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ, имеет вид = 0?
- Волна распространяется со скоростью 6м / с при частоте 5Гц?
- Длина морской волны — 180 м, период — 9 с?
- . Вдоль натянутого шнура распространяется поперечная волна?
- Волна распространяется со скоростью 4м / с при частоте колебаний 8гц?
- Волна распространяется со скоростью 1, 5 м / с?
- Известно, что скорость упругой волны, распространяющейся в древесине вдоль её волокон, в 4 раза больше, чем скорость такой же волны, распространяющейся поперек её волокон?
- Вдоль натянутого шнура распространяется поперечная волна ?
- Что принимается за единицу длины световой волны в СИ, если волна распространяется в воде?
- Известно, что скорость упругой волны, распространяющейся в древесине вдоль ее волокон, в 4 раза больше, чем скорость такой же волны, распространяющейся поперек ее волокон?
- Плоская электромагнитная волна распространяется в вакууме вдоль оси оZ на каком минимальном расстояние друг от друга (выраженном в единицах длины волны (лямда) ) находиться в точке для которых разност?
- М 1000 м 500 м 6,28 м
- 📺 Видео
Видео:Распространение колебаний в среде. Волны | Физика 9 класс #28 | ИнфоурокСкачать

Если уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ, имеет вид = 0?
Физика | 10 — 11 классы
Если уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ, имеет вид = 0.
14x) то длина волны.
K — волновое число
k = 2 * π / λ = > ; λ = 2 * π / k = 6, 28 / 3, 14 = 2, 00 м.
Видео:10й класс; Физика; "Уравнение плоской волны"Скачать

Волна распространяется со скоростью 6м / с при частоте 5Гц?
Волна распространяется со скоростью 6м / с при частоте 5Гц.
Чему равна длина волны?
Видео:Получение уравнения плоской бегущей волны.Скачать

Длина морской волны — 180 м, период — 9 с?
Длина морской волны — 180 м, период — 9 с.
С какой скоростью распространяется волна?
Видео:Вывод волнового уравненияСкачать

. Вдоль натянутого шнура распространяется поперечная волна?
. Вдоль натянутого шнура распространяется поперечная волна.
Найдите скорость волны, если частота колебаний частиц в волне 1, 5 Гц , а длина волны 2м.
Видео:*** Лекция. Волновое уравнение электромагнитной волны ******Скачать

Волна распространяется со скоростью 4м / с при частоте колебаний 8гц?
Волна распространяется со скоростью 4м / с при частоте колебаний 8гц.
Какова длинна волны?
Видео:Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать

Волна распространяется со скоростью 1, 5 м / с?
Волна распространяется со скоростью 1, 5 м / с.
Частота волны 5Гц.
Чему равна длина волны.
Видео:Распространение волн в упругих средах. Звуковые волны | Физика 11 класс #18 | ИнфоурокСкачать

Известно, что скорость упругой волны, распространяющейся в древесине вдоль её волокон, в 4 раза больше, чем скорость такой же волны, распространяющейся поперек её волокон?
Известно, что скорость упругой волны, распространяющейся в древесине вдоль её волокон, в 4 раза больше, чем скорость такой же волны, распространяющейся поперек её волокон.
Определите длину волны, распространяющейся вдоль её волокон, если скорость волны от того же источника, распространяющейся поперек волокон равна 1, 2 км / c.
Частота колебаний равна 10кГц.
Видео:Урок №45. Электромагнитные волны. Радиоволны.Скачать

Вдоль натянутого шнура распространяется поперечная волна ?
Вдоль натянутого шнура распространяется поперечная волна .
Найдите скорость волны если частота колебаний частиц в волне 1.
5 Гц , а длина волны 2 м .
Видео:Билет №34 "Электромагнитные волны"Скачать

Что принимается за единицу длины световой волны в СИ, если волна распространяется в воде?
Что принимается за единицу длины световой волны в СИ, если волна распространяется в воде?
Видео:Физика 9 класс (Урок№12 - Волновые явления. Длина волны. Скорость распространения волн.)Скачать

Известно, что скорость упругой волны, распространяющейся в древесине вдоль ее волокон, в 4 раза больше, чем скорость такой же волны, распространяющейся поперек ее волокон?
Известно, что скорость упругой волны, распространяющейся в древесине вдоль ее волокон, в 4 раза больше, чем скорость такой же волны, распространяющейся поперек ее волокон.
Определите длину волны, распространяющейся вдоль волокон, если скорость волны от того же источника, распространяющейся поперек волокон, равна 1, 2 м / с.
Частота колебаний равна 10 кГц.
Видео:Электромагнитные волны | Физика 9 класс #44 | ИнфоурокСкачать

Плоская электромагнитная волна распространяется в вакууме вдоль оси оZ на каком минимальном расстояние друг от друга (выраженном в единицах длины волны (лямда) ) находиться в точке для которых разност?
Плоская электромагнитная волна распространяется в вакууме вдоль оси оZ на каком минимальном расстояние друг от друга (выраженном в единицах длины волны (лямда) ) находиться в точке для которых разность фаз колибаний вектора магнитной индукции составляет П / 2 ?
Вопрос Если уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ, имеет вид = 0?, расположенный на этой странице сайта, относится к категории Физика и соответствует программе для 10 — 11 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.
Видео:Урок 384. Излучение электромагнитных волн.Скачать

М 1000 м 500 м 6,28 м
Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ, имеет вид ξ= 0,01sin10 3 (t – 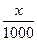
М 1000 м 500 м 6,28 м
Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ, имеет вид ξ= 0,01sin10 3 (t – 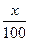
М 0,628 м 100 м 6,28 м
Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ, имеет вид ξ= 0,01sin10 3 (t – 
М 0,314 м 50 м 6,28 м
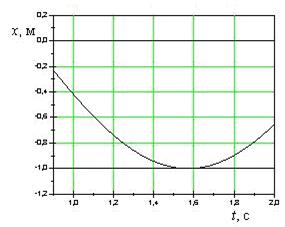
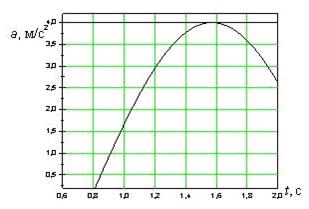
На рисунках изображены зависимости от времени координаты и ускорения материальной точки, колеблющейся по гармоническому закону.
Циклическая частота колебаний точки равна ….
1 с -1 3 с -1 4 с -1 2 с -1
Уравнение движения пружинного маятника 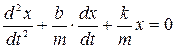
Вынужденных колебаний свободных незатухающих колебаний
📺 Видео
9 класс, 35 урок, Длина волны. Скорость распространения волнСкачать

Электромагнитные волны и уравнения Максвелла — Эмиль АхмедовСкачать

41 Шкала электромагнитных волнСкачать

Электромагнитные волны. Шкала электромагнитных волн. Практическая часть - решение задачи. 9 класс.Скачать

Раскрытие тайн электромагнитной волныСкачать

Парадокс электромагнитной волныСкачать

Физика. 10 класс. Основное уравнение динамики вращательного движенияСкачать