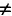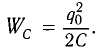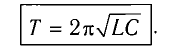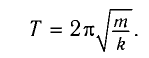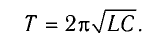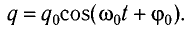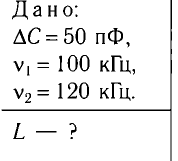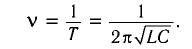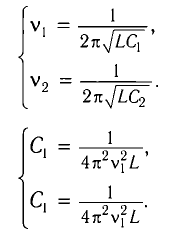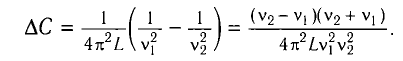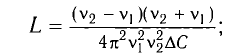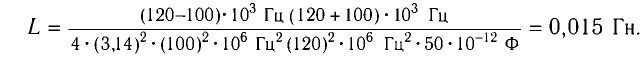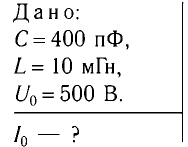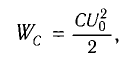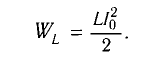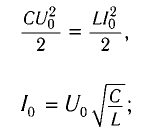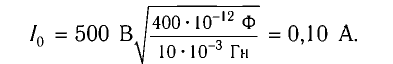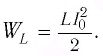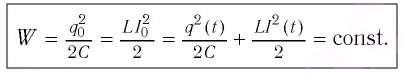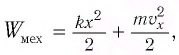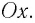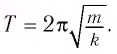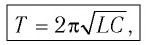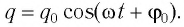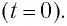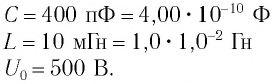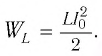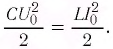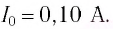Электромагнитные колебания и волны
Уравнение изменения со временем тока в колебательном контуре имеет вид I = − 0,02 sin400πt А. Индуктивность контура L = 1 Гн. Найти период T колебаний, емкость С контура, максимальную энергию Wм магнитного поля и максимальную энергию Wэл электрического поля.
Дано:
I = − 0,02 sin 400 π t А
Решение:
Период колебаний находим по формуле Томсона
Циклическая частота связана с периодом соотношением
Тогда период колебаний
Максимальная энергия Wм магнитного поля
По закону сохранения энергии максимальная энергия Wэл электрического поля будет равна максимальной энергии магнитного поля
- Уравнение i = 10 ^ — 4cos(wt + pi / 2) выражает зависимость силы тока от времени в колебательном контуре?
- Определите индуктивность катушки колебательного контура, если амплитудное значение силы тока в катушке Io = 20мА, амплитудное значение напряжения на конденсаторе Uo = 400В?
- Заряд на обкладках конденсатора колебательного контура изменяется по закону q = 8 * 10 ^ — 7 cos800t?
- Колебательный контур настроен на частоту 20 МГц?
- Максимальное напряжение на конденсаторе колебательного контура составляет 90В?
- Конденсатору с ёмкость 10нФ колебательного контура был сообщён заряд 0, 1 мКл?
- Решите пожалуйста 3 задачи1) В колебательном контуре индуктивность катушки L = 1 мГн, емкость конденсатора С = 0, 4 мкФ?
- В колебательном контуре емкость конденсатора 3 мкФ, а максимальнаянапряжение на нем 4 В?
- В колебательном контуре максимальное значение напряжения на конденсаторе 120 В?
- Максимальная энергия конденсатора в колебательном контуре 0, 2 Дж?
- В состав колебательного контура входит :Конденсатор?
- Колебательный контур в физике — формулы и определения с примерами
- Колебательный контур и свободные электромагнитные колебания в контуре
- 📹 Видео
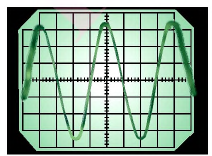
Видео:На рисунке приведён график зависимости силы тока от времени в колебательном контуре с - №30252Скачать

Уравнение i = 10 ^ — 4cos(wt + pi / 2) выражает зависимость силы тока от времени в колебательном контуре?
Физика | 10 — 11 классы
Уравнение i = 10 ^ — 4cos(wt + pi / 2) выражает зависимость силы тока от времени в колебательном контуре.
В некоторый момент времени i = 10 ^ — 4A, при этом энергия : 1.
В конденсаторе и катушке максимальны 2.
В конденсаторе максимальна, в катушке минимальна 3.
В конденсаторе минимальна, в катушке максимальна 4.
В конденсаторе и катушке минимальны.
Колебательный контур — электрическая цепь, состоящая из емкости (конденсатора) С и индуктивности (катушки) L.
Полная энергия, запасенная в колебательном контуре, при отсутствии потерь (идеальный контур) сохраняется : W = Wинд + Wкон = const (1)Ток в цепи подчиняется гармоническому закону : $i = i_0 cos (omega t + varphi)$.
Причем максимальных значений ток достигает тогда, когда конденсатор полностью разряжен, т.
Е. его энергия равна нулю : $W_ = frac = 0$, при этом энергия в катушке из соотношения (1) максимальна и равна : $W_ = frac
По условию задачи в некоторый момент времени ток равен своей амплитуде, т.
Е. он достиг своего максимального значения.
Значит, верный ответ — 3.
Видео:Графические зависимости заряда и силы тока от времени в идеальном колебательном контуре. 11 класс.Скачать

Определите индуктивность катушки колебательного контура, если амплитудное значение силы тока в катушке Io = 20мА, амплитудное значение напряжения на конденсаторе Uo = 400В?
Определите индуктивность катушки колебательного контура, если амплитудное значение силы тока в катушке Io = 20мА, амплитудное значение напряжения на конденсаторе Uo = 400В.
Электроемкость конденсатора контура C = 50 пФ.
Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Заряд на обкладках конденсатора колебательного контура изменяется по закону q = 8 * 10 ^ — 7 cos800t?
Заряд на обкладках конденсатора колебательного контура изменяется по закону q = 8 * 10 ^ — 7 cos800t.
Индуктивность контура 2Гн.
Найдите электроёмкость конденсатора и максимальное значение энергии электрического поля конденсатора и магнитного поля катушки индуктивности.
Видео:Колебательный контур | ЕГЭ Физика | Николай НьютонСкачать

Колебательный контур настроен на частоту 20 МГц?
Колебательный контур настроен на частоту 20 МГц.
В процессе колебаний максимальная сила тока на катушке достигает 12 мА, а амплитуда колебаний напряжения на конденсаторе 6.
Чему равна индуктивность катушки в колебательном контуре?
Видео:Урок 353. Колебательный контурСкачать

Максимальное напряжение на конденсаторе колебательного контура составляет 90В?
Максимальное напряжение на конденсаторе колебательного контура составляет 90В.
Какова максимальная сила тока в контуре если ёмкость конденсатора 5мкФ, а индуктивность катушки 0, 2 Гн?
Полное решение пожалуйста).
Видео:Урок 147 (осн). Сила тока. Единицы силы тока. АмперметрыСкачать

Конденсатору с ёмкость 10нФ колебательного контура был сообщён заряд 0, 1 мКл?
Конденсатору с ёмкость 10нФ колебательного контура был сообщён заряд 0, 1 мКл.
Определите максимальную силу тока в контуре, если индуктивность катушки 4 Гн.
Видео:По графику зависимости заряда конденсатора от времени, определите амплитуду силы тока в катушкеСкачать

Решите пожалуйста 3 задачи1) В колебательном контуре индуктивность катушки L = 1 мГн, емкость конденсатора С = 0, 4 мкФ?
Решите пожалуйста 3 задачи
1) В колебательном контуре индуктивность катушки L = 1 мГн, емкость конденсатора С = 0, 4 мкФ.
Чему равна амплитуда силы тока в контуре, если амплитуда заряда конденсатора q = 1 мкКл?
2) В колебательном контуре индуктивность катушки L = 1 мГн, емкость конденсатора С = 0, 4 мкФ.
Чему равна амплитуда напряжения на конденсаторе, если амплитуда силы тока в катушке 50 мА?
3) В колебательном контуре сила тока через катушку, индуктивность которой 1 мГн, меняется со временем по закону и = 10 ^ — 3 sin (10 ^ 4t), A.
Какое максимальное значение имеет энергия магнитного поля катушки?
Видео:Урок 354. Математическое описание процессов в колебательном контуреСкачать

В колебательном контуре емкость конденсатора 3 мкФ, а максимальнаянапряжение на нем 4 В?
В колебательном контуре емкость конденсатора 3 мкФ, а максимальная
напряжение на нем 4 В.
Найдите максимальную энергию магнитного поля катушки.
Активный сопротивлением контура пренебреч.
Видео:Урок 358. Активное сопротивление в цепи переменного тока. Действующее значение тока и напряженияСкачать

В колебательном контуре максимальное значение напряжения на конденсаторе 120 В?
В колебательном контуре максимальное значение напряжения на конденсаторе 120 В.
Определите максимальную силу тока, если индуктивность катушки 5 мГн, емкость конденсатора 10мкФ.
Видео:Энергии в колебательном контуре зад 11 клСкачать

Максимальная энергия конденсатора в колебательном контуре 0, 2 Дж?
Максимальная энергия конденсатора в колебательном контуре 0, 2 Дж.
Чему равна энергия конденсатора в момент когда энергия магнитного поля катушки равно 50 мДж.
Видео:Уравнение силы переменного тока в цепи RLEСкачать

В состав колебательного контура входит :Конденсатор?
В состав колебательного контура входит :
Конденсатор и катушка
Трансформатор и резистор.
Если вам необходимо получить ответ на вопрос Уравнение i = 10 ^ — 4cos(wt + pi / 2) выражает зависимость силы тока от времени в колебательном контуре?, относящийся к уровню подготовки учащихся 10 — 11 классов, вы открыли нужную страницу. В категории Физика вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы.
Видео:Физика 11 класс (Урок№7 - Свободные и вынужденные электромагнитные колебания. Колебательный контур.)Скачать

Колебательный контур в физике — формулы и определения с примерами
Колебательный контур:
Явление возникновения ЭДС индукции при изменении магнитного потока через площадь, ограниченную контуром, называется явлением электромагнитной индукции.
Под явлением самоиндукции понимают возникновение в контуре ЭДС индукции, создаваемой вследствие изменения силы тока в самом контуре. Правило Ленца: возникающий в замкнутом контуре индукционный ток имеет такое направление, при котором созданный им собственный магнитный поток через площадь, ограниченную контуром, стремится компенсировать изменение внешнего магнитного потока, вызвавшее данный ток.
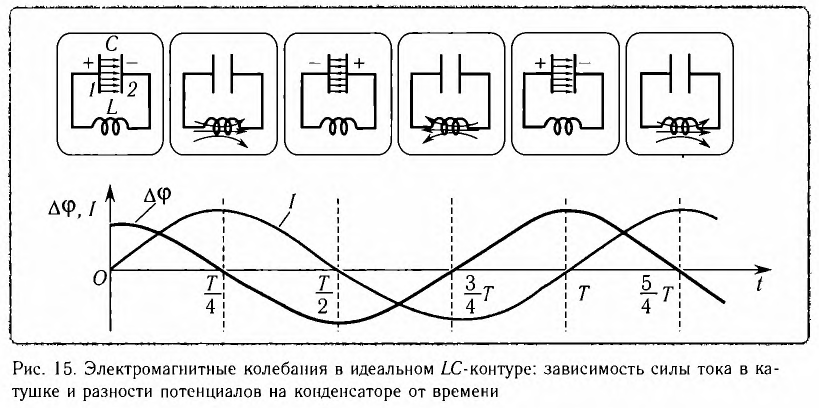
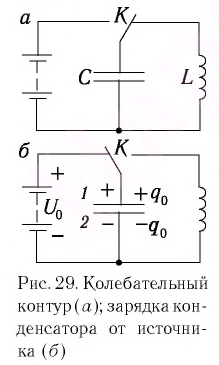
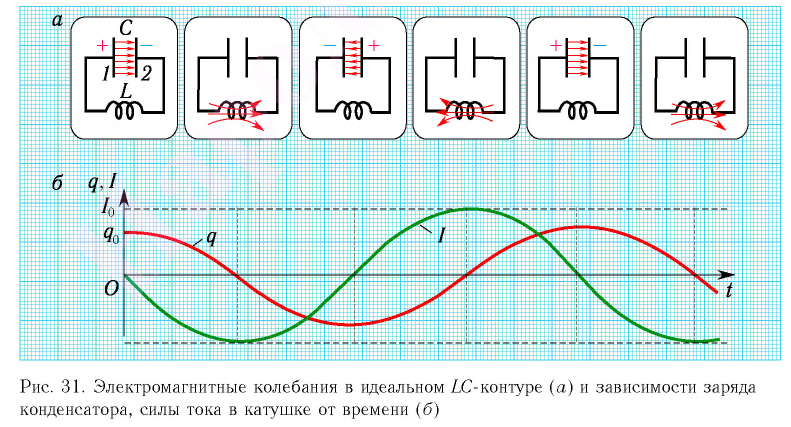
Рассмотрим электрическую цепь, содержащую конденсатор электроемкостью С и катушку (соленоид) индуктивностью L (рис. 15). Такая цепь называется идеальным колебательным контуром или LC-контуром.
В отличие от реального колебательного контура, который всегда обладает некоторым электрическим сопротивлением (R
Пусть в начальный момент времени (t = 0) конденсатор С заряжен так, что на его первой обкладке находится заряд +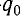

С течением времени конденсатор начнет разряжаться, и в цепи появится электрический ток, сила l(t) которого будет меняться с течением времени. Поскольку при прохождении такого электрического тока в катушке индуктивности возникнет изменяющийся во времени магнитный поток, то это вызовет появление ЭДС самоиндукции, препятствующей изменению силы тока.
Вследствие этого сила тока в колебательном контуре будет возрастать от нуля до максимального значения в течение некоторого промежутка времени, определяемого индуктивностью катушки.
В момент полной разрядки конденсатора (q = 0) сила тока в катушке I(t) достигнет своего максимального значения 
После разрядки конденсатора сила тока в катушке начнет убывать. Это также произойдет не мгновенно, поскольку вновь возникающая ЭДС самоиндукции согласно правилу Ленца создаст индукционный ток. Он будет иметь такое же направление, как и уменьшающийся ток в цепи, и поэтому будет «поддерживать» его. Индукционный ток, создаваемый ЭДС самоиндукции катушки, перезарядит конденсатор до начального напряжения обратной полярности — знак заряда на каждой обкладке окажется противоположным начальному.
Соответственно, к моменту исчезновения тока заряд конденсатора достигнет максимального значения 
Таким образом, в идеальном LC-контуре будут происходить периодические изменения значений силы тока и напряжения, причем полная энергия контура будет оставаться постоянной. В этом случае говорят, что в контуре возникли свободные электромагнитные колебания.
Свободные электромагнитные колебания в LC-контуре — это периодические изменения заряда на обкладках конденсатора, силы тока и напряжения в контуре, происходящие без потребления энергии от внешних источников.
Таким образом, возникновение свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора и возникновением в катушке ЭДС самоиндукции, которая «обеспечивает» эту перезарядку. Заметим, что заряд q(t) конденсатора и сила тока I(t) в катушке достигают своих максимальных значений 

Наименьший промежуток времени, в течение которого LC-контур возвращается в исходное состояние (к начальному значению заряда данной обкладки), называется периодом свободных (собственных) электромагнитных колебаний в контуре.
Период свободных электромагнитных колебаний в контуре определяется по формуле Томсона:
Получим эту формулу, используя закон сохранения энергии. Поскольку полная энергия идеального LC-контура, равная сумме энергий электростатического поля конденсатора и магнитного поля катушки, сохраняется, то в любой момент времени справедливо равенство
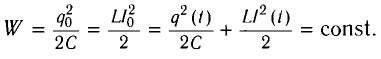
Поскольку закономерности гармонических колебаний носят универсальный характер, то можно сравнить колебания в LC-контуре с колебаниями пружинного маятника.
Для пружинного маятника полная механическая энергия в любой момент времени 2 ,
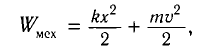
и период его колебаний
Проанализируем соотношения (1) и (2). Сравним выражения для энергии электростатического поля конденсатора 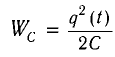
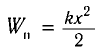
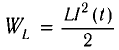
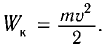
Следуя аналогии, заменим в формуле для периода колебаний пружинного маятника т на L и k на 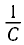
Несложные дальнейшие рассуждения позволяют установить аналогии между физическими величинами при электромагнитных и механических колебаниях (табл. 4).
Таблица 4
Сопоставление физических величин, характеризующих электромагнитные и механические колебания
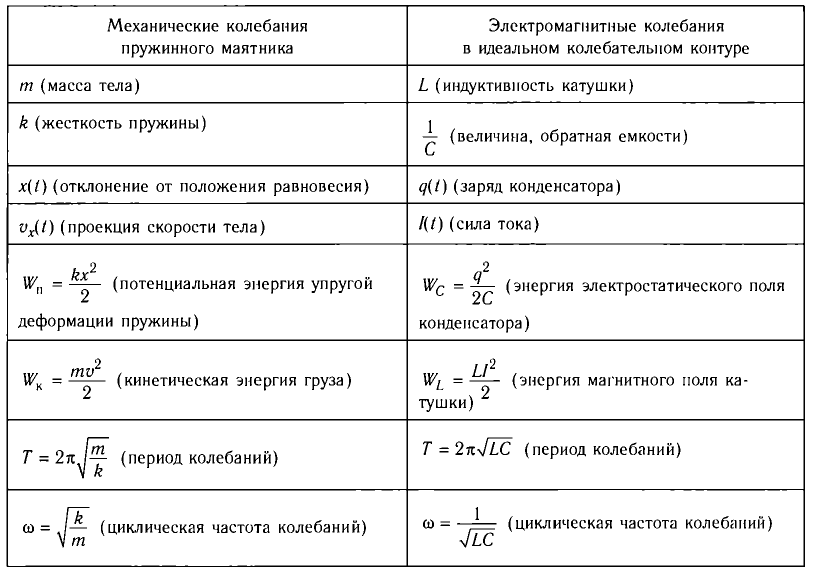
Соответственно, зависимость заряда конденсатора от времени будет иметь такой же характер, как и зависимость координаты (смещения) тела, совершающего гармонические колебания, от времени:
Также по гармоническому закону (но с другими начальными фазами) будут изменяться сила тока в цепи, напряжение на конденсаторе.
Для определения начальной фазы 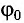
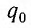
Полная энергия идеального колебательного контура (R = 0) с течением времени сохраняется, поскольку в нем при прохождении тока теплота не выделяется.
Как уже отмечалось, реальный колебательный контур всегда имеет некоторое сопротивление R, обусловленное сопротивлением катушки, соединительных проводов и т. д. Это приводит к тому, что электромагнитные колебания в реальном контуре с течением времени затухают, тогда как в идеальном контуре они «будут происходить» сколь угодно долго.
Таким образом, механическим аналогом идеального колебательного контура является пружинный маятник без трения, а механическим аналогом реального колебательного контура — пружинный маятник с трением.
Пример №1
При изменении емкости конденсатора идеального LC-контура на 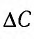
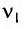
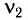
Решение
Частота колебаний в контуре
Поскольку частота колебаний в контуре увеличилась (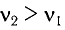
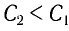
Из условия задачи получаем систему уравнений
Откуда
Вычитая из первого уравнения второе, получаем
Ответ: L = 0,015 Гн.
Пример №2
Колебательный контур состоит из конденсатора емкостью С = 400пФ и катушки индуктивностью L=10 мГн. Определите амплитудное значение силы тока 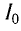
Решение
Максимальная энергия электростатического поля конденсатора
а максимальная энергия магнитного поля катушки
Так как контур идеальный (R = 0), то его полная энергия не меняется с течением времени. Кроме того, в момент, когда заряд конденсатора максимален, сила тока в катушке равна нулю, а в момент, когда заряд конденсатора равен нулю, сила тока в ней максимальна. Это позволяет утверждать, что максимальные энергии в конденсаторе и катушке равны: 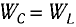
откуда
Ответ: 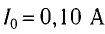
Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Колебательный контур и свободные электромагнитные колебания в контуре
Явление возникновения ЭДС в любом контуре при изменении магнитного потока через поверхность, ограниченную контуром, называется явлением электромагнитной индукции.
Под явлением самоиндукции понимают возникновение в замкнутом проводящем контуре ЭДС индукции, создаваемой вследствие изменения силы тока в самом контуре.
Правило Ленца: возникающий в замкнутом проводящем контуре индукционный ток имеет такое направление, при котором созданный им магнитный поток через поверхность, ограниченную контуром, стремится компенсировать изменение магнитного потока, вызвавшее данный ток.
Рассмотрим электрическую цепь, состоящую из последовательно соединенных конденсатора электроемкостью 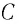
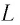
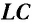
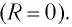
Подключив (при помощи ключа 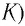
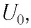
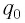
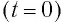
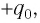
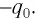
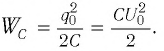
Рассмотрим процесс разрядки конденсатора в колебательном контуре. После соединения заряженного конденсатора с катушкой (при помощи ключа 
Таким образом, в контуре появится нарастающий по модулю электрический ток, сила 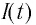
Вследствие этого модуль силы тока в колебательном контуре будет в течение некоторого промежутка времени плавно возрастать от нуля до максимального значения 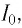
При разрядке конденсатора энергия его электростатического поля превращается в энергию магнитного поля катушки с током. Согласно закону сохранения энергии суммарная энергия идеального колебательного контура остается постоянной с течением времени (уменьшение энергии электростатического поля конденсатора равно увеличению энергии магнитного поля катушки):
где 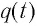
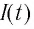
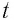
В момент полной разрядки конденсатора 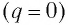
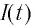
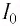
После разрядки конденсатора сила тока в катушке начинает убывать по модулю. Это также происходит не мгновенно, поскольку вновь возникающая ЭДС самоиндукции согласно правилу Ленца создает индукционный ток. Он имеет такое же направление, как и уменьшающийся по модулю ток в цепи, и поэтому «поддерживает» его. Индукционный ток, создаваемый ЭДС самоиндукции катушки, перезаряжает конденсатор до начального напряжения 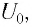
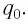
Таким образом, в идеальном 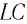
Свободные электромагнитные колебания в LC-контуре — это периодические изменения заряда на обкладках конденсатора, силы тока и напряжения в контуре, происходящие без пополнения энергии от внешних источников.
Таким образом, существование свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора, вызванной возникновением ЭДС самоиндукции в катушке. Заметим, что заряд 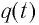
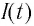
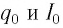
Наименьший промежуток времени, в течение которого LC-контур возвращается в исходное состояние (к начальным значениям заряда на каждой из обкладок), называется периодом свободных (собственных) электромагнитных колебаний в контуре.
Получим формулу для периода свободных электромагнитных колебаний в контуре, используя закон сохранения энергии. Поскольку полная энергия идеального 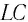
Процессы, происходящие в колебательном контуре, аналогичны колебаниям пружинного маятника. Для полной механической энергии пружинного маятника в любой момент времени:
где 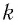
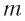
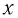
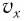
Период его колебаний:
Проанализируем соотношения (1) и (2). Видно, что энергия электростатического поля конденсатора 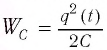
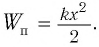
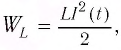
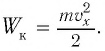
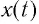
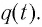
Следуя проведенной аналогии, заменим в формуле для периода колебаний пружинного маятника массу 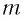
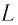
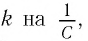
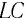
которая называется формулой Томсона.
Несложные дальнейшие рассуждения позволяют установить аналогии между физическими величинами при электромагнитных и механических колебаниях (табл. 4).

Зависимость заряда конденсатора от времени имеет такой же вид, как и зависимость координаты (проекции смещения) тела, совершающего гармонические колебания, от времени:
Также по гармоническому закону изменяются сила тока (но с другой начальной фазой) в цепи и напряжение на конденсаторе.
Для определения начальной фазы 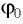
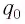
Отметим, что колебательный контур, в котором происходит только обмен энергией между конденсатором и катушкой, называется закрытым.
Полная энергия идеального колебательного контура 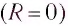
Таким образом, механическим аналогом идеального колебательного контура является пружинный маятник без учета трения, а механическим аналогом реального колебательного контура — пружинный маятник с учетом трения.
Пример решения задачи:
Идеальный колебательный контур состоит из конденсатора емкостью 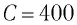
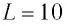
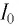
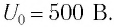
Дано:

Решение
Максимальная энергия электростатического поля конденсатора:
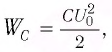
а максимальная энергия магнитного поля катушки:
Так как контур идеальный 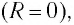
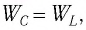
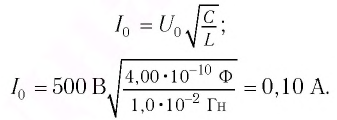
Ответ:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Исследовательские методы в физике
- Вертикальное движение тел в физик
- Неравномерное движение по окружности
- Равномерное движение по окружности
- Распространение механических волн в средах
- Электромагнитное поле
- Опыты Фарадея в физике
- Электромагниты и их применение в физике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
📹 Видео
Урок 92 (осн). Колебательное движение. МаятникиСкачать

Физика| Колебательные процессы. Часть 1Скачать

Урок 361. Вынужденные колебания в последовательном колебательном контуреСкачать

Расчет амплитудного значения силы тока при гармонических электромагнитных колебаниях.Скачать

Свободные электромагнитные колебания. 11 класс.Скачать

11 класс урок №10 Решение задач Электромагнитные колебанияСкачать

Урок 383. Вихревое электрическое поле. Ток смещенияСкачать