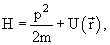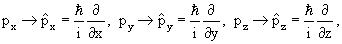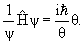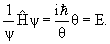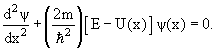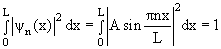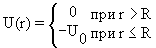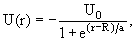Аналог классического волнового уравнения был предложен Э. Шредингером в 1925 г. Как и классическое уравнение, уравнение Шредингера связывает производные волновой функции по времени и координате. Уравнение Шредингера описывает поведение любых нерелятивистских систем. На примерах частицы, находящейся в бесконечно глубокой яме, и гармонического осциллятора рассмотрены простейшие квантовые системы, получены дискретные спектры состояний. Возможности описания динамики данных систем ограничены набором квантовых чисел, отражающих универсальные и внутренние симметрии квантовых систем.
- 4.1. Уравнение Шредингера
- Уравнение Шредингера
- 4.2. Частица в одномерной прямоугольной яме с бесконечными стенками
- 4.3. Гармонический осциллятор
- Частица в одномерной потенциальной яме
- 4.4. Частица в поле с центральной симметрией
- 4.5. Орбитальный момент количества движения
- 4.6. Спин
- 4.7. Полный момент количества движения
- 4.8. Квантовые числа
- Таблица квантовых чисел
- Задачи
- СТАЦИОНАРНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
- Вывод уравнения Шредингера
- 🔍 Видео
4.1. Уравнение Шредингера
В квантовой физике изменение состояния частицы описывается уравнением Шредингера
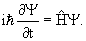 | (4.1) |
где 
в которой 







х → 


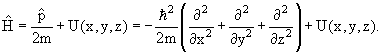 | (4.2) |
Уравнение Шредингера
Зависящее от времени уравнение Шредингера:
где 
Разделение переменных. Запишем Ψ(




Левая часть является функцией только координат, а правая не зависит от переменной x. Поэтому обе части последнего уравнения должны быть равны одной и той же постоянной, которую обозначим E
θ(t) = exp(−iEt/ћ), 




Уравнение 


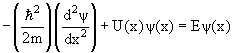
Для трехмерной системы с массой m в поле с потенциалом U(
−(ћ 2 /2m)Δψ(



где Δ – лапласиан.
Так как уравнение Шредингера является линейным уравнением первого порядка по времени, то с его помощью по заданному значению волновой функции Ψ(x, y, z, 0) в момент времени t = 0 можно найти её значение в произвольный момент времени t − Ψ(x, y, z, t).
Уравнение Шредингера для стационарного состояния, когда потенциальная энергия частицы не зависит от времени, имеет вид
 ψ( ψ( ) = Eψ( ) = Eψ( ). ). | (4.3) |
Это уравнение называют стационарным уравнением Шредингера.
Так как в стационарном состоянии
Ψ( ,t) = ψ( ,t) = ψ( )exp(−iEt/ћ) )exp(−iEt/ћ) | (4.4) |
и вероятность найти частицу в момент t в точке x, y, z пропорциональна |Ψ(
|ψ(x,y,z)| 2 , т.е. не зависит от времени. Аналогично, вероятность обнаружить значение физической величины, характеризующей систему, также не изменяется со временем, поскольку выражается через квадрат модуля волновой функции.
4.2. Частица в одномерной прямоугольной яме с бесконечными стенками
Потенциальная энергия U(x) в прямоугольной яме удовлетворяет следующим условиям:
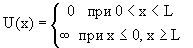 | (4.5) |
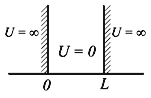
Рис.4.1. Прямоугольная яма с бесконечными стенками
Частица находится в области 0 ≤ x ≤ L. Вне этой области ψ(x) = 0. Уравнение Шредингера для частицы, находящейся в области 0 ≤ x ≤ L
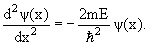 | (4.6) |
Волновая функция, являющаяся решением уравнения (4.9), имеет вид
| ψ(x)= Аsin kx + Bcos kx, | (4.7) |
где k = (2mE/ћ 2 ) 1/2 . Из граничных условий ψ(0) = 0, ψ(L) = 0 и условий непрерывности волновой функции следует
| Аsin kL = 0. | (4.8) |
kL = nπ, n = 1, 2, 3, … , то есть внутри потенциальной ямы с бесконечно высокими стенками устанавливаются стоячие волны, а энергия состояния частиц имеет дискретный спектр значений En
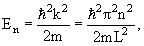 n = 1, 2, 3, … n = 1, 2, 3, … | (4.9) |
Частица может находиться в каком-то одном из множества дискретных состояний, доступных для неё.
Каждому значению энергии En соответствует волновая функция ψn(x), которая с учетом условия нормировки
 | (4.10) |
В отличие от классической, квантовая частица в прямоугольной яме не может иметь энергию
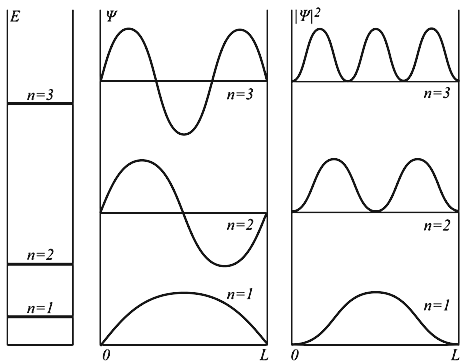
E 2 π 2 /(2mL 2 ). Состояния частицы ψn в одномерном поле бесконечной потенциальной ямы полностью описывается с помощью одного квантового числа n. Спектр энергий дискретный.
Рис. 4.2. Уровни энергии и волновые функции частицы Ψ в бесконечной прямоугольной яме. Квадрат модуля волновой функции |Ψ| 2 определяет вероятность нахождения частицы в различных точках потенциальной ямы.
4.3. Гармонический осциллятор
Положение уровней частицы в потенциальной яме зависит от вида потенциальной ямы. В одномерной потенциальной яме гармонического осциллятора потенциальная энергия имеет вид
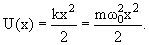 | (4.11) |
В этом случае одномерное уравнение Шредингера имеет вид
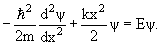 | (4.12) |
Допустимые значения полной энергии определяются формулой
| En = ћω0(n + 1/2), n = 0, 1, 2, | (4.13) |
В отличие от бесконечной прямоугольной ямы, спектр уровней гармонического осциллятора эквидистантный.
С увеличением массы частицы или размеров области ее локализации квантовое описание частицы переходит в классическое.
Частица в одномерной потенциальной яме
Одномерная прямоугольная яма шириной L:
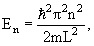

Одномерный гармонический осциллятор:
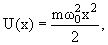
4.4. Частица в поле с центральной симметрией
В сферических координатах стационарное уравнение Шредингера для частицы в центральном потенциале U(r) имеет вид
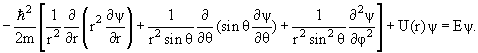 | (4.14) |
Решение уравнения (4.14) записываются в виде произведения радиальной и угловой функций
| ψ(r,θ,φ) = Rnl(r)Ylm(θ,φ), | (4.15) |
где радиальная функция Rnl(r) и угловая функция Ylm(θ,φ), называемая сферической, удовлетворяют уравнениям
 2 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) 2 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) | (4.16) |
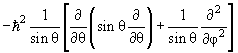 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) 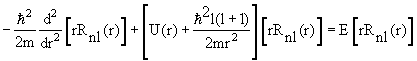 | (4.17) |
Уравнение (4.16) определяет возможные собственные значения l и собственные функции Ylm(θ,φ) оператора квадрата момента 
Схема уровней (последовательность и абсолютные значения энергий) зависит от радиальной функции Rnl(r), которая в свою очередь определяется потенциалом U(r), в котором находится частица.
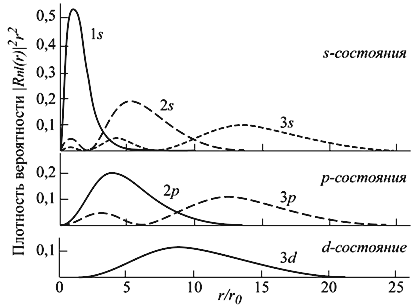
Рис. 4.3. Радиальное распределение вероятности нахождения электрона в кулоновском поле протона (атом водорода). Расстояния даны в боровских радиусах
r0 = ћ 2 /mee 2 ≈ 0.529·10 8 cм.
| Решения уравнения |
существуют лишь при определенных значениях квантовых чисел n (радиальное квантовое число), l (орбитальное квантовое число) и m (магнитное квантовое число).
Возможные энергетические состояния системы (уровни энергии) определяются числами n и l и в случае сферически симметричных состояний не зависят от квантового числа m. Число n может быть только целым:
n = 1, 2, …, ∞. Число l может принимать значения 0, 1, 2, …, ∞.
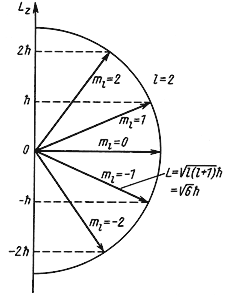
4.5. Орбитальный момент количества движения
Собственные значения L 2 и Lz являются решением уравнений


Они имеют следующие дискретные значения
L 2 = ћ 2 l(l + 1), где l = 0, 1, 2, 3, …,
Lz = ћm, где m = 0, ± 1, ± 2, ± 3,…, ± l.
Для характеристики состояний с различными значениями орбитального момента l обычно используют следующие обозначения:
Спектроскопические названия орбитальных моментов l
| l = 0 | s-состояние |
| l = 1 | p-состояние |
| l = 2 | d-состояние |
| l = 3 | f-состояние |
| l = 4 | g-состояние |
| l = 5 | h-состояние |
| и. т. д. |
Состоянию с l = 0 отвечает сферически симметричная волновая функция. В тех случаях, когда l ≠ 0 волновая функция не имеет сферической симметрии. Симметрия волновой функции определяется симметрией сферических функций Ylm(θ,φ). Имеет место интересное квантовое явление, когда решение сферически симметричной задачи (потенциал описывает сферически симметричную систему) приводит к состояниям, не обладающим сферической симметрией. Таким образом, симметрия уравнений не обязательно должна отражаться в симметрии каждого отдельно взятого решения этих уравнений, а лишь во всей совокупности этих решений.
Для частицы, находящейся в сферически симметричном потенциале, величина орбитального момента количества движения L:
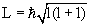 | (4.18) |
Обычно, для упрощения, когда говорят о величине орбитального момента количества движения, называют этой величиной квантовое число l, имея в виду, что между l и L имеется однозначная связь (4.18).
Рис. 4.4 Возможные ориентации вектора 
Так как величина l может принимать только целочисленные значения 0, 1, 2, 3,…, то и орбитальный момент количества движения L квантуется. Например, для частицы с l = 2 момент количества движения
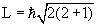
= 6.58·10 -22 √6 МэВ·сек ≈ 2.6·10 — 34 Дж·сек.
Пространственное квантование. Орбитальный момент количества движения является векторной величиной. Так как величина орбитального момента количества движения квантуется, то и направление 

Состояние частицы, находящейся в сферически симметричном поле, полностью описывается тремя квантовыми числами: n, l и m.
Появление квантовых чисел связано со свойствами симметрии системы. Характер этой симметрии определяет возможные значения квантовых чисел. Очевидно, что система, описываемая функцией e im φ , примет прежнее значение только тогда, когда азимутальный угол φ в результате поворота вокруг оси z примет прежнее значение φ. Этому условию функция e im φ удовлетворяет только в случае, когда величина mφ кратна 2π. Т.е. величина m должна иметь целые значения. Так как необходимо учитывать вращение в двух противоположных направлениях и отсутствие вращения, единственно возможными значениями оказываются m = 0, ±1, ±2, … .
4.6. Спин
Спин − собственный момент количества движения частицы. Между значением вектора спина 

 2 = ћ 2 s(s + 1) 2 = ћ 2 s(s + 1) | (4.19) |
В отличие от орбитального квантового числа l, которое может быть лишь целым числом или нулем, спиновое квантовое число s (в дальнейшем просто спин) может быть как целым (включая нуль), так и полуцелым, т. е. s = 0, 1/2, 1, 3/2, 2, 5/2, … , но при этом для каждой элементарной частицы спин может принимать единственное присущее этому типу частиц значение. Так, спины π-мезонов и К-мезонов равны 0. Спины электрона, протона, нейтрино, кварков и их античастиц равны 1/2. Спин фотона равен 1. Бозоны составляют класс частиц с целым значением спина, спин фермионов имеет полуцелое значение. Спин частицы невозможно изменить, также как её заряд или массу. Это её неизменная квантовая характеристика.
Как и в случае других квантовых векторов, проекция вектора спина 
szћ = ±sћ, ±(s − 1)ћ, ±(s − 2)ћ. ±1/2ћ или 0.
Число sz − это квантовое число проекции спина. Максимальная величина sz совпадает с s. Так как спин электрона равен 1/2, то проекция этого спина может принимать лишь два значения sz = ±1/2. Если проекция +1/2, то говорят, что спин направлен вверх, если проекция -1/2, то говорят, что спин направлен вниз.
4.7. Полный момент количества движения
Полный момент количества движения частицы или системы частиц 





Квадрат полного момента имеет значение:

Квантовое число полного момента j, соответствующее сумме двух векторов 

j = l + s, l + s −1. |l − s|
Проекция 
Число значений проекции Jz равно 2j + 1. Если для 

4.8. Квантовые числа
Квантовые числа – это целые или дробные числа, которые определяют все возможные значения физической величины, характеризующей различные квантовые системы – атомы, атомные ядра, кварки и другие частицы.
Таблица квантовых чисел
| n | Радиальное квантовое число. Определяет число узлов волновой функции и энергию системы. n = 1, 2, …, ∞. |
| J, j | Полный угловой момент J и его квантовое число j. Последнее никогда не бывает отрицательным и может быть целым или полуцелым в зависимости от свойств рассматриваемой системы.  2 = ћ 2 j(j + 1). 2 = ћ 2 j(j + 1). |
| L, l | Орбитальный угловой момент L и его квантовое число l. Интерпретация l такая же, как j, но l может принимать только целые значения, включая нуль: l = 0, 1, 2,…. L 2 = ћ 2 l(l + 1). |
| m | Магнитное квантовое число. Проекция полного или орбитального углового момента на выделенную ось (обычно ось z) равна mћ. Для полного момента m = ±j, ±(j-1), …, ±1/2 или 0. Для орбитального m = ± l, ± (l-1), …, ±1, 0. |
| S, s | Спиновый угловой момент S и его квантовое число s. Оно может быть либо положительным целым (включая нуль), либо полуцелым. s – неизменная характеристика частицы определенного типа. S 2 = ћ 2 s(s + 1). |
| sz | Квантовое число проекции спинового момента частицы на выделенную ось. Эта проекция может принимать значения szћ, где sz = ± s, ± (s -1), …, ±1/2 или 0. |
| P или π | Пространственная четность. Характеризует поведение системы при пространственной инверсии  → — → —  (зеркальном отражении). Полная четность частицы Р = π(-1) l , где π – её внутренняя четность, а (-1) l – её орбитальная четность. Внутренние четности кварков положительные, антикварков — отрицательные. (зеркальном отражении). Полная четность частицы Р = π(-1) l , где π – её внутренняя четность, а (-1) l – её орбитальная четность. Внутренние четности кварков положительные, антикварков — отрицательные. |
| I | Изоспин. Характеризует свойство зарядовой инвариантности сильных взаимодействий |
Для обозначения спинового момента часто используют букву J.
Все состояния, в которых может находиться квантовая система, описываются с помощью полного набора квантовых чисел. Так в случае протона в ядре состояние протона описывается с помощью четырех квантовых чисел, соответствующих четырем степеням свободы – трем пространственным координатам и спину. Это
- Радиальное квантовое число n ( 1, 2, …, ∞),
- Орбитальное квантовое число l (0, 1, 2, …),
- Проекция орбитального момента m (± l, ± (l-1), …, ±1, 0),
- Спин протона s =1/2.
Для описания сферически-симметричных систем в квантовой физике используются различные сферически симметричные потенциалы с различной радиальной зависимостью:
- Кулоновский потенциал U = Q/r,
- Прямоугольная потенциальная яма
- Потенциал типа гармонического осциллятора U = kr 2 ,
- Потенциал Вудса-Саксона (с его помощью описываются внутриядерные взаимодействия):
где U0, а и R – положительные константы (R – радиус ядра). Во всех случаях сферически симметричные системы можно описать с помощью набора квантовых чисел n, l, j, jz, однако, в зависимости от радиального вида потенциала энергетический спектр состояний системы будет различным.
Существование сохраняющихся во времени физических величин тесно связано со свойствами симметрии гамильтониана системы. Например, в случае, если квантовая система обладает центральной симметрией U = U(r), то этой системе соответствует сохранение орбитального момента количества движения l и одной из его проекций m. При этом из-за сферической симметрии задачи энергия состояний не будет зависеть от величины m, т. е. состояния будут вырожденными по m.
Наряду с пространственными симметриями, связанными с непрерывными преобразованиями, в квантовой физике существуют и другие симметрии – дискретные. Одной из них является зеркальная симметрия волновой функции относительно инверсии координат (

Система тождественных частиц характеризуется еще одной симметрией – симметрией относительно перестановок тождественных частиц. Эта симметрия определяется свойствами частиц, образующих систему. Системы частиц с целым спином (бозонов) описываются симметричными волновыми функциями, системы частиц с полуцелым спином (фермионов) − антисимметричными волновыми функциями.
Задачи
4.1. Вычислите допустимые уровни энергии электрона, находящегося в одномерной прямоугольной потенциальной яме шириной 10 -8 см, протона, находящегося в потенциальной яме 5 Фм, и шарика массой 1 г, находящегося в потенциальной яме 1 см.
4.2. Рассчитать энергию перехода между состояниями 1s и 2s в атоме водорода.
4.3. Найти значение полного момента j для протона в d-состоянии. Каким будет результат измерения полного момента протона в состоянии 1d5/2?
4.4. Найти полный момент (квантовое число j) системы двух нуклонов в s‑состоянии (l = 0).
4.5. Какие значения может иметь полный момент системы j, если
А. Нейтрон и протон находятся в состояниях с |l,s:j>n = |1, 1 /2: 3 /2>, |l,s:j>p = |1, 1 /2: 3 /2>?
Б. Два нейтрона находятся в состояниях с |l,s:j>1 = |1, 1 /2: 3 /2> и |l,s:j>2 = |1, 1 /2: 3 /2>?
4.6. А) Нейтрон находится в p-состоянии. Найти значения полного момента j и возможные значения проекции момента jz. Каким будет результат измерения орбитального момента частицы в этом состоянии? Б) Рассмотрите задачу А) для протона в d-состоянии.
Ответ: А) j = 3/2, 1/2; jz = ±3/2, ±1/2; L = ћ√ l(l +1) = √ 2 ћ;
Б) j = 5/2, 3/2; jz = ±5/2, ±3/2, ±1/2; L = ћ√ l(l +1) = √ 6 ћ
4.7. А) Частица с собственным моментом s = 3/2 находится в состоянии с орбитальным моментом
l = 2. Найти полный момент частицы j.
Б) Частица с собственным моментом s = 1/2 находится в состоянии с орбитальным моментом
l = 3. Определите полный момент частицы j
Ответ: А) j = 7/2 ÷ 1/2; Б) j = 7/2, 5/2
4.8. Протон и нейтрон находятся в состоянии с относительным орбитальным моментом L = 1. Найти полный момент системы J.
Ответ: J = 0, 1, 2
4.9. На оболочке с квантовым числом n = 1, l = 2 находятся протон и нейтрон. Определить их суммарный полный момент J и его проекцию Jz. Изменится ли результат, если на оболочке n = 1,
l = 2 будут находиться два нейтрона?
4.10. Почему возникают вырожденные состояния?
4.11. Написать оператор Гамильтона 
4.12. Напишите стационарное уравнение Шредингера в сферической системе координат.
4.13. Какие квантовые числа характеризуют частицу в центрально-симметричной потенциальной яме?
4.14. Покажите, что волновые функции ψ = Aexp(kx −ωt) и ψ = Asin(kx −ωt) не удовлетворяют зависящему от времени уравнению Шредингера.
4.15. Покажите, что волновые функции ψ = Ae i(kx −ωt) и ψ = A(cos(kx −ωt) − sin(kx −ωt))удовлетворяют зависящему от времени уравнению Шредингера.
4.16. Частица находится в низшем состоянии n = 1 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L.
А) Рассчитайте вероятность обнаружить частицу в интервале Δx = 0.001L при x = 1 /2L, x = 2 /3L, x = L.
Б) Рассмотрите случай, когда частица находится в состоянии n = 2 при тех же значениях x.
Ответ: А) P(L/2) = 0.002; P(2L/3) = 0.0015; P(L) = 0; Б) P(L/2) = 0; P(2L/3) = 0.0015; P(L) = 0
4.17. Частица находится в состоянии n = 2 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L. Рассчитайте вероятность обнаружить частицу в интервале ( 1 /3L, 2 /3L).
Ответ: P(L/3, 2L/3) = 0.2
4.18. Электрон находится всостонии n = 5 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L. Рассчитайте вероятность обнаружить электрон в области x от 0.2L до 0.5L.
Ответ: P(0.2L, 0.5L) = 0.3
4.19. Электрон находится в бесконечно глубокой одномерной потенциальной яме. Рассчитайте ширину потенциальной ямы, если энергия состояния n = 1 равна 0.1 эВ.
Ответ: L = 1.9 нм
4.20. Рассчитайте средние значения и 2 > для состояний n = 1, 2, 3 в бесконечно глубокой прямоугольной потенциальной яме.
4.21. Что общего и в чем различие в описании атома водорода в теории Шредингера и в модели Бора?
4.22. Почему энергии атома водорода в теории Шредингера не зависят от орбитального квантового числа l?
4.23. Угловой момент характеризуется квантовым числом l = 3. Какие значения могут принимать Lz и L 2 ?
Ответ: Lz = -3ћ, -2ћ. 3ћ; L 2 = 12ћ 2
4.24. Угловой момент характеризуется квантовым числом l = 3. Какие значения могут принимать Lz и L 2 ?
Видео:Урок 455. Уравнение ШрёдингераСкачать

СТАЦИОНАРНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
ОПИСАНИЕ ПОВЕДЕНИЯ ЭЛЕКТРОНА В КВАНТОВОЙ МЕХАНИКЕ
1. Уравнение Шредингера
Для выполнения лабораторных работ 6 и 7 необходимо знакомство с основами квантовой механики. Остановимся на тех её положениях, которые непосредственно связаны с содержанием данных работ.
В них изучается поведение микрочастицы (электрона) в определенных внешних условиях. Это означает, что потенциальная энергия электрона U, Обусловленная его взаимодействием с окружающими объектами, является известной функцией координат: 




Называемое Временны́м уравнением Шредингера, где I – мнимая единица, ( H – постоянная Планка), Ñ2 – оператор Лапласа (имеющий в декартовых координатах вид 


2. Уравнение Шредингера для стационарных состояний
Среди решений уравнения (Б.1) особый интерес представляют волновые функции вида

Описывающие состояния, называемые Стационарными. Легко проверить, что волновая функция вида (2) будет решением уравнения Шредингера (1), если 

Где 



Уравнение (3) называется Уравнением Шредингера для стационарных Состояний, или Стационарным уравнением Шредингера. Существенно, что стационарное уравнение Шредингера имеет физически приемлемые решения, вообще говоря, не для любых значений Е, А лишь для некоторого множества 


3. Волновая функция и заключенная в ней информация
Как уже говорилось, волновая функция описывает состояние частицы. Это означает, что в 

(звездочка обозначает комплексное сопряжение). Важную информацию о движении частицы дает выражающийся через 

Называемый вектором плотности потока вероятности. Он указывает направление наиболее быстрого перемещения вероятности и дает скорость этого перемещения. Смысл величин (4) и (5) раскрывается в эксперименте, когда производится N Измерений над электроном в одном и том же состоянии. Тогда при больших значениях N должно выполняться: DN¢ / N

J , где DN¢ – число электронов, обнаруженных в единичном объеме вблизи точки (Х, у, z), а DN¢¢ – результирующее число электронов, прошедших за единицу времени в направлении вектора 
В связи с приведенной интерпретацией выражений (4) и (5) волновую функцию 
Отметим, что для стационарных состояний выражения (4) и (5) не зависят от времени и что для вещественных 

4. Оптическая аналогия
Анализируя квантовомеханическую задачу, полезно сопоставлять ее, с одной стороны, с аналогичной задачей классической механики, а с другой – с некоторой оптической задачей. В классической механике аналогом, очевидно, будет задача о частице такой же массы, движущейся в силовом поле, характеризуемом той же потенциальной энергией , что и в исходной квантовой. Выяснив характер движения классической частицы, можно лучше понять особенности ее квантовомеханического поведения. Оптическим аналогом для квантовомеханической задачи с
E = Const будет, Как можно показать, задача о распространении монохроматической световой волны в неоднородной среде, для которой показатель преломления N Изменяется по закону

Отметим, что длину волны при этом можно оценивать по соотношению де Бройля 

Аналогия с оптикой позволяет во многих случаях, не решая уравнение Шредингера, предвидеть и объяснить качественно поведение y-функции, а следовательно и частицы.
5. Одномерные квантовомеханические задачи
Среди квантовомеханических задач выделяются своей простотой одномерные, т. е. такие, в которых U = U ( X ), а волновую функцию 

А стационарное уравнение Шредингера сводится к уравнению в обыкновенных производных

Уравнение (8) решается особенно просто, когда ось X можно разбить на области, в каждой из которых потенциал U(X) принимает постоянные значения, а на границах соседних областей испытывает скачок. Такой потенциал называется Прямоугольным Из-за прямых углов на его графике. Строго говоря, такие потенциалы не реализуемы, поскольку им соответствуют бесконечные силы в точках скачков потенциальной энергии. Все же прямоугольные потенциалы дают грубое представление о многих реальных системах, позволяя получать полезные результаты крайне простыми математическими методами.
В области, где потенциал U Постоянен, при E > U стационарное уравнение Шредингера (8) сводится к уравнению
Где 

Где А И В – произвольные постоянные.
При этом, в соответствии с (9) и (7), зависящая от времени
Волновая функция 

В котором первое слагаемое описывает волну, бегущую вправо, а второе – влево. При переходе от одной области к другой U изменяется и, следовательно, изменяется длина волны. Существенно, что на границе между областями, как уже отмечалось, y(Х) и ее первая производная D Y / D x должны быть непрерывны. Это приводит к двум уравнениям связи между амплитудными коэффициентами А и В для соседних областей.
6. Движение электрона в области потенциальной ступеньки
Рассмотрим случай, когда потенциал испытывает только один скачок (Потенциальная Ступенька, рис. 1). Предположим, что электроны с некоторой энергией Е Приходят слева. Согласно классической механике электроны должны беспрепятственно проходить точку Х = 0, поскольку в этой точке они испытывает действие силы, направленной в сторону своего движения (ускоряющей силы).
Используем, прежде всего, оптическую аналогию. Согласно (6) при X= 0 происходит скачкообразное изменение показателя преломления N , а при падении света на поверхность раздела двух сред с различными N часть волны отражается от неё, а часть проходит во вторую среду. Поэтому следует ожидать отражения в точке Х = 0 и для y-волны, а следовательно, отличной от нуля вероятности отражения электрона при падении на скачок потенциала как справа, так и слева.
Подтвердим эти предположения строгим расчетом на основе стационарного уравнения Шредингера (8). В области I, слева от скачка потенциала (т. е. при Х 0) для случая, когда электроны падают только слева, решение содержит лишь одно слагаемое, соответствующее прошедшей волне

Где 







Поскольку K2 > K1 , амплитуды отраженной и падающей волн имеют противоположные знаки. Это означает, что для падающей слева волны её фаза при отражении от скачка потенциала изменяется на π – происходит «потеря» полуволны.
Плотность потока электронов Г может быть выражена через их концентрацию Пе И скорость v : Г = Ne V. Поскольку Пе

K|ψ|2. Доля электронов, которые проходят вправо, т. е. коэффициент прохождения DЕ,, равен отношению плотности прошедшего потока к плотности падающего:

Аналогично рассчитывается и коэффициент отражения:

Те же выражения получаются в результате подсчета коэффициентов 



Вытекающим непосредственно из определения вектора плотности потока вероятности 
Легко проверить также, что 

Следует подчеркнуть, что свойство отражения частиц от скачков потенциала является чисто квантовомеханическим эффектом. Оно вытекает из волновых свойств материи и не имеет места в классической физике.
В заключение сформулируем квантовомеханическую задачу, позволяющую на примере одномерной прямоугольной симметричной потенциальной ямы (рис. 2) простыми методами рассмотреть квантование энергии электрона и дать качественное объяснение эффекта Рамзауэра.
В этой задаче потенциальная энергия электрона U (Х) задается в виде:


Величина L = 2 а – Ширина ямы, 
В зависимости от полной энергии электрона E, Возникают три случая:
Видео:Уравнение Шредингера Стационарные состоянияСкачать

Вывод уравнения Шредингера
Квантовая теория родилась в 1900 г., когда Макс Планк предложил теоретический вывод о соотношении между температурой тела и испускаемым этим телом излучением — вывод, который долгое время ускользал от других ученых, Как и его предшественники, Планк предположил, что излучение испускают атомные осцилляторы, но при этом считал, что энергия осцилляторов (и, следовательно, испускаемого ими излучения) существует в виде небольших дискретных порций, которые Эйнштейн назвал квантами. Энергия каждого кванта пропорциональна частоте излучения. Хотя выведенная Планком формула вызвала всеобщее восхищение, принятые им допущения оставались непонятными, так как противоречили классической физике.
В 1905 г. Эйнштейн воспользовался квантовой теорией для объяснения некоторых аспектов фотоэлектрического эффекта — испускания электронов поверхностью металла, на которую падает ультрафиолетовое излучение. Попутно Эйнштейн отметил кажущийся парадокс: свет, о котором на протяжении двух столетий было известно, что он распространяется как непрерывные волны, при определенных обстоятельствах может вести себя и как поток частиц.
Примерно через восемь лет Нильс Бор распространил квантовую теорию на атом и объяснил частоты волн, испускаемых атомами, возбужденными в пламени или в электрическом заряде. Эрнест Резерфорд показал, что масса атома почти целиком сосредоточена в центральном ядре, несущем положительный электрический заряд и окруженном на сравнительно больших расстояниях электронами, несущими отрицательный заряд, вследствие чего атом в целом электрически нейтрален. Бор предположил, что электроны могут находиться только на определенных дискретных орбитах, соответствующих различным энергетическим уровням, и что «перескок» электрона с одной орбиты на другую, с меньшей энергией, сопровождается испусканием фотона, энергия которого равна разности энергий двух орбит. Частота, по теории Планка, пропорциональна энергии фотона. Таким образом, модель атома Бора установила связь между различными линиями спектров, характерными для испускающего излучение вещества, и атомной структурой. Несмотря на первоначальный успех, модель атома Бора вскоре потребовала модификаций, чтобы избавиться от расхождений между теорией и экспериментом. Кроме того, квантовая теория на той стадии еще не давала систематической процедуры решения многих квантовых задач.
Новая существенная особенность квантовой теории проявилась в 1924 г., когда де Бройль выдвинул радикальную гипотезу о волновом характере материи: если электромагнитные волны, например свет, иногда ведут себя как частицы (что показал Эйнштейн), то частицы, например электрон при определенных обстоятельствах, могут вести себя как волны. В формулировке де Бройля частота, соответствующая частице, связана с ее энергией, как в случае фотона (частицы света), но предложенное де Бройлем математическое выражение было эквивалентным соотношением между длиной волны, массой частицы и ее скоростью (импульсом). Существование электронных волн было экспериментально доказано в 1927 г. Клинтоном Дэвиссоном и Лестером Джермером в Соединенных Штатах и Джоном-Паджетом Томсоном в Англии.
Под впечатлением от комментариев Эйнштейна по поводу идей де Бройля Шрёдингер предпринял попытку применить волновое описание электронов к построению последовательной квантовой теории, не связанной с неадекватной моделью атома Бора. В известном смысле он намеревался сблизить квантовую теорию с классической физикой, которая накопила немало примеров математического описания волн. Первая попытка, предпринятая Шрёдингер в 1925 г., закончилась неудачей.
Скорости электронов в теории II Шрёдингер были близки к скорости света, что требовало включения в нее специальной теории относительности Эйнштейна и учета предсказываемого ею значительного увеличения массы электрона при очень больших скоростях.
Одной из причин постигшей Шрёдингер неудачи было то, что он не учел наличия специфического свойства электрона, известного ныне под названием спина (вращение электрона вокруг собственной оси наподобие волчка), о котором в то время было мало известно.
Следующую попытку Шрёдингер предпринял в 1926 г. Скорости электронов на этот раз были выбраны им настолько малыми, что необходимость в привлечении теории относительности отпадала сама собой.
Вторая попытка увенчалась выводом волнового уравнения Шрёдингера, дающего математическое описание материи в терминах волновой функции. Шрёдингер назвал свою теорию волновой механикой. Решения волнового уравнения находились в согласии с экспериментальными наблюдениями и оказали глубокое влияние на последующее развитие квантовой теории.
Незадолго до того Вернер Гейзенберг, Макс Борн и Паскуаль Иордан опубликовали другой вариант квантовой теории, получивший название матричной механики, которая описывала квантовые явления с помощью таблиц наблюдаемых величин. Эти таблицы представляют собой определенным образом упорядоченные математические множества, называемые матрицами, над которыми по известным правилам можно производить различные математические операции. Матричная механика также позволяла достичь согласия с наблюдаемыми экспериментальными данными, но в отличие от волновой механики не содержала никаких конкретных ссылок на пространственные координаты или время. Гейзенберг особенно настаивал на отказе от каких-либо простых наглядных представлений или моделей в пользу только таких свойств, которые могли быть определены из эксперимента.
Шрёдингер показал, что волновая механика и матричная механика математически эквивалентны. Известные ныне под общим названием квантовой механики, эти две теории дали долгожданную общую основу описания квантовых явлений. Многие физики отдавали предпочтение волновой механике, поскольку ее математический аппарат был им более знаком, а ее понятия казались более «физическими»; операции же над матрицами — более громоздкими.
Функция Ψ. Нормировка вероятности.
Обнаружение волновых свойств микрочастиц свидетельствовало о том, что классическая механика не может дать правильного описания поведения подобных частиц. Возникла необходимость создать механику микрочастиц, которая учитывала бы также и их волновые свойства. Новая механика, созданная Шрёдингером, Гайзенбергом, Дираком и другими, получила название волновой или квантовой механики.
Плоская волна де Бройля
<img src="http://ic3.static.km.ru/img/61658
является весьма специальным волновым образованием, соответствующим свободному равномерному движению частицы в определенном направлении и с определенным импульсом. Но частица, даже в свободном пространстве и в особенности в силовых полях, может совершать и другие движения, описываемые более сложными волновыми функциями. В этих случаях полное описание состояния частицы в квантовой механике дается не плоской волной де Бройля, а какой-то более сложной комплексной функцией <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/61658
004.gif» />, зависящей от координат и времени. Она называется волновой функцией. В частном случае свободного движения частицы волновая функция переходит в плоскую волну де Бройля (1). Сама по себе волновая функция вводится как некоторый вспомогательный символ и не относится к числу непосредственно наблюдаемых величин. Но ее знание позволяет статистически предсказывать значения величин, которые получаются экспериментально и потому имеют реальный физический смысл.
Через волновую функцию определяется относительная вероятность обнаружения частицы в различных местах пространства. На этой стадии, когда говорится только об отношениях вероятностей, волновая функция принципиально определена с точностью до произвольного постоянного множителя. Если во всех точках пространства волновую функцию умножить на одно и то же постоянное (вообще говоря, комплексное) число, отличное от нуля, то получится новая волновая функция, описывающая в точности то же состояние. Не имеет смысла говорить, что Ψ равна нулю во всех точках пространства, ибо такая «волновая функция» никогда не позволяет заключить об относительной вероятности обнаружения частицы в различных местах пространства. Но неопределенность в определении Ψ можно значительно сузить, если от относительной вероятности перейти к абсолютной. Распорядимся неопределенным множителем в функции Ψ так, чтобы величина |Ψ|2dV давала абсолютную вероятность обнаружения частицы в элементе объема пространства dV. Тогда |Ψ|2 = Ψ*Ψ (Ψ* — комплексно сопряжённая с Ψ функция) будет иметь смысл плотности вероятности, которую следует ожидать при попытке обнаружения частицы в пространстве. При этом Ψ будет определена все еще с точностью до произвольного постоянного комплексного множителя, модуль которого, однако, равен единице. При таком определении должно быть выполнено условие нормировки:
<img src="http://ic3.static.km.ru/img/61658
где интеграл берется по всему бесконечному пространству. Оно означает, что во всем пространстве частица будет обнаружена с достоверностью. Если интеграл от |Ψ|2 берётся по определённому объёму V1 – мы вычисляем вероятность нахождения частицы в пространстве объёма V1.
Нормировка (2) может оказаться невозможной, если интеграл (2) расходится. Так будет, например, в случае плоской волны де Бройля, когда вероятность обнаружения частицы одинакова во всех точках пространства. Но такие случаи следует рассматривать как идеализации реальной ситуации, в которой частица не уходит на бесконечность, а вынуждена находиться в ограниченной области пространства. Тогда нормировка не вызывает затруднений.
Итак, непосредственный физический смысл связывается не с самой функцией Ψ, а с ее модулем Ψ*Ψ. Почему же в квантовой теории оперируют с волновыми функциями Ψ, а не непосредственно с экспериментально наблюдаемыми величинами Ψ*Ψ? Это необходимо для истолкования волновых свойств вещества — интерференции и дифракции. Здесь дело обстоит совершенно так же, как во всякой волновой теории. Она (во всяком случае в линейном приближении) принимает справедливость принципа суперпозиции самих волновых полей, а не их интенсивностей и, таким образом, достигает включения в теорию явлений интерференции и дифракции волн. Так и в квантовой механике принимается в качестве одного из основных постулатов принцип суперпозиции волновых функций, заключающийся в следующем.
Если <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/61658
008.gif» />– волновые функции, описывающие какие-то два состояния частицы, то всякая их линейная комбинация с постоянными коэффициентами с1Ψ1 + с2Ψ2 представляет также волновую функцию той же частицы, описывающую какое-то ее состояние. Найдя Ψ указанным путем, можно в дальнейшем определить и плотность вероятности Ψ*Ψ в состоянии Ψ.
Оправданием такого принципа суперпозиции является согласие с опытом вытекающих из него следствий. Является ли принцип суперпозиции точным законом природы, или он верен только в линейном приближении, этот вопрос не может считаться выясненным.
Подчеркнем особо, что физический смысл волновой функции Ψ связан не только с ее модулем, но и с ее фазой, определяемой мнимой частью этой функции. Если бы речь шла о волновой функции только одного состояния, то можно было бы ограничиться одним только модулем. Но если речь идет о наложении состояний, то происходит их интерференция, а она определяется относительной разностью фаз волновых функций, описывающих эти состояния.
Частота волны де Бройля ω и вообще частота волновой функции относятся к принципиально ненаблюдаемым величинам. Этим можно воспользоваться, чтобы перейти к квантовой механике в нерелятивистской форме. И в классической механике обширная область явлений охватывается в нерелятивистском приближении. То же может быть сделано и в квантовой механике. К тому же здесь переход к релятивистскому рассмотрению осложняется следующим обстоятельством. В сильных полях, когда энергия поля (например, γ-кванта) превосходит 2mес2, начинается рождение пар электрон-позитрон. То же наблюдается в аналогичных случаях и для других частиц. По этой причине последовательная релятивистская квантовая механика не может быть теорией одного тела (одной частицы). Теория одного тела возможна только в нерелятивистском приближении. Поэтому в дальнейшем мы ограничимся только нерелятивистской квантовой механикой.
В нерелятивистской квантовой механике мы будем по-прежнему пользоваться соотношениями:
E=ħω, <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/61658
(Здесь и далее: Е – энергия объекта (кинетическая), <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/61658
012.gif» />-импульс, <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/61658
014.gif» />- волновой вектор, ħ – постоянная Планка, делённая на 2π, ħ = 1,05459∙10-34 Дж∙с, ω – частота (волн де Бройля)).
Однако собственную энергию частицы m0c2 учитывать не будем. Это значит, что, начиная с этого места, мы вводим новую частоту, отличающуюся от прежней частоты на постоянную. Для новой частоты сохраним прежнее обозначение ω. В частности, в случае свободного движения
E = р2/2m, и закон дисперсии записывается в виде
Это приводит к выражению для фазовой скорости волн де Бройля:
υф = ω/k = ħk/2m = υ/2 (5) (здесь k=2π/λ, — волновое число)
Однако это не может отразиться на физических выводах теории, так как фазовая скорость, как и сама частота ω волны де Бройля, относится к числу принципиально ненаблюдаемых величин. Существенно, что физически наблюдаемые величины — плотность вероятности Ψ*Ψ и групповая скорость (групповая скорость волн де Бройля равна скорости частицы) — при новом выборе частоты остаются неизменными. Остаются неизменными и все величины, доступные измерению на опыте.
3. Получение уравнения Шрёдингера
Основная задача волновой механики состоит в нахождении волновых функций и связанных с ними физических следствий в самых разнообразных условиях. Для ее решения служит волновое уравнение, найденное Шрёдингером в 1926 г. Это — основное уравнение квантовой механики, но оно справедливо только в нерелятивистской квантовой механике, т. е. в случае движений, медленных по сравнению со скоростью света в вакууме.
Уравнение Шрёдингера должно быть общим уравнением, т. е. должно быть пригодно для решения всех, а не только частных задач. Поэтому в него не должны входить значения параметров (например, начальные условия, конкретный вид силовых полей и пр.), выделяющие частные виды движения. В него могут входить мировые постоянные, например постоянная Планка. Могут входить массы и импульсы частиц, но их численные значения не должны быть конкретизированы. Силовые поля, в которых движется частица, также должны быть представлены в общем виде. Здесь дело обстоит так же, как с уравнениями Ньютона или Максвелла, которые приспособлены для решения всех, а не только частных механических или электродинамических задач. Кроме того, надо потребовать, чтобы уравнение Шрёдингера было линейно и однородно по Ψ. Этим будет обеспечена справедливость принципа суперпозиции волновых функций, необходимость которого диктуется интерференцией и дифракцией волн вещества.
При отыскании уравнения Шрёдингера заметим, что одним из решений его в свободном пространстве должна быть плоская волна де Бройля (1). Найдем дифференциальное уравнение, удовлетворяющее перечисленным выше условиям, решением которого является эта волна.
Дифференцирование <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/61658
002.gif» /> (1) по x, y, z даст:
<img src="http://ic3.static.km.ru/img/61658
Сложением полученных вторых производных найдем:
<img src="http://ic3.static.km.ru/img/61658
Учитывая соотношения (3) найдём, что k2=p2/ħ2, таким образом, имеем:
<img src="http://ic3.static.km.ru/img/61658
Это дифференциальное уравнение, но не то, которое мы ищем. Действительно, при выводе величина p предполагалась постоянной, а потому уравнение (6) описывает конкретное движение с заданным постоянным импульсом.
Продифференцируем теперь (1) по времени при постоянной ω:
<img src="http://ic3.static.km.ru/img/61658
Учитывая (3), находим что <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/61658
025.gif» />, таким образом можно записать:
<img src="http://ic3.static.km.ru/img/61658
Это уравнение также не годится. Оно описывает движение частицы в свободном пространстве с постоянной кинетической энергией E. Однако, выразим из (7) энергию, а из (6) – квадрат импульса p2:
<img src="http://ic3.static.km.ru/img/61658
Учтём, что в нерелятивистской механике, в отсутствии потенциальных сил, E= p2/2m. Подставив в эту формулу полученные выражения для энергии и импульса, придём к однородному линейному уравнению
<img src="http://ic3.static.km.ru/img/61658
<img src="http://ic3.static.km.ru/img/61658
Это уравнение уже не содержит никаких индивидуальных параметров, выделяющих конкретное движение. Это уравнение и есть уравнение Шрёдингера в отсутствии силовых полей.
Обобщим теперь полученное уравнение (8) на случай движений в силовых полях. Ограничимся случаем потенциальных силовых полей, которые, как и в классической механике, характеризуются потенциальной функцией или потенциальной энергией U(<img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/61658
035.gif» />). Заметим теперь, что ħ/дt имеет размерность энергии, Значит, одинаковую размерность имеют
и величины <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/61658
037.gif» />и U(<img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/61658
035.gif» />)Ψ. Поэтому прибавление в правой части уравнения (8) слагаемого U(<img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/61658
035.gif» />)Ψ не меняет размерности этого уравнения. Можно думать, что полученное таким путем уравнение
<img src="http://ic3.static.km.ru/img/61658
будет правильно учитывать влияние потенциального силового поля на движение частицы. Это и есть уравнение Шрёдингера. Это так называемое уравнение Шрёдингера, зависящее от времени. Его также называют общим уравнением Шрёдингера.
Путь, которым мы пришли к уравнению Шрёдингера, конечно, не может служить доказательством этого уравнения. Но уравнение Шрёдингера – существенно новый принцип. Его нельзя логически вывести из старых принципов, в которых он не содержится. Единственным доказательством уравнения Шрёдингера является только опыт – опытная проверка всех выводимых из него следствий. Такую проверку уравнение Шрёдингера выдержало.
В уравнении (9) в неявной форме уже заложена двойственная – корпускулярно-волновая –природа вещества. Согласно интерпретации волновой функции Ψ частица не локализована. Она, как принято говорить, с определенной вероятностью «размазана» в пространстве. Казалось бы, что при написании уравнения (9) это обстоятельство с самого начала должно быть принято во внимание, т. е. под U следовало бы понимать потенциальную энергию частицы с учетом всех возможных положений ее и их вероятностей. На самом деле в уравнении (9) это не предполагается. Потенциальная функция U(<img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/61658
035.gif» />) рассматривается в нем так же, как в классической физике, т. е. как функция локализованной, в частности точечной, частицы в силовом поле. Например, в атоме водорода для электрона в поле ядра полагают U(r) = -е2/r, т. е. поступают так же, как если бы обе эти частицы были локализованы.
Уравнение Шрёдингера – первого порядка по времени. Отсюда следует, что заданием волновой функции Ψ во всем пространстве в какой-либо момент времени (например, принимаемый за начальный) однозначно определяется функция Ψ также во всем пространстве во все последующие моменты времени. Не следует смотреть на это утверждение как на выражение принципа причинности в квантовой механике. Ибо выражаемая им «причинность» относится к волновой функции Ψ. А волновая функция связана с реально наблюдаемыми объектами вероятностными соотношениями. Поэтому квантовая механика, по крайней мере в современной ее форме, является принципиально статистической теорией.
Уравнение Шрёдингера, как это требовалось с самого начала для выполнения принципа суперпозиции, линейно и однородно относительно функции Ψ. В точной математической форме принцип суперпозиции сводится к двум утверждениям.
Во-первых, если Ψ1 и Ψ2 — какие-либо два решения уравнения Шрёдингера, то и всякая линейная комбинация их α1Ψ1 + α2Ψ2 с постоянными (вообще говоря, комплексными) коэффициентами α1 и α2 есть также решение того же уравнения. Во-вторых, если волновые функции Ψ1 и Ψ2 описывают какие-либо два состояния системы, то и линейная комбинация α1Ψ1 + α2Ψ2 также описывает какое-то состояние той же системы. Конечно, состояние частицы определяется не самими коэффициентами α1 и α2, а только их отношением α1/α2 . Состояние не изменится, если оба коэффициента умножить на одну и ту же вещественную или комплексную постоянную. Это позволяет, например, функцию Ψ = α1Ψ1 + α2Ψ2 нормировать (если интеграл <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/61658
041.gif» />, взятый по всему пространству, сходится).
Особое значение в квантовой механике имеют стационарные состояния. Это – такие состояния, в которых все наблюдаемые физические параметры не меняются с течением времени. Сама волновая функция Ψ не относится к этим параметрам. Она принципиально не наблюдаема. Не должны меняться во времени только физически наблюдаемые величины, которые могут быть образованы из Ψ по правилам квантовой механики.
Как следует из уравнения (9), вид волновой функции Ψ определяется потенциальной энергией U, т. е., в конечном счете, характером тех сил, которые действуют на частицу. Вообще говоря, U есть функция координат и времени. Для стационарного (не меняющегося со временем) силового поля U не зависит явно от времени. В последнем случае волновая функция Ψ распадается на два множителя, один из которых зависит только от времени, второй – только от координат:
<img src="http://ic3.static.km.ru/img/61658
(Е — полная энергия частицы, (E/ħ) = ω ).
Учтём, что дифференциал <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/61658
Подстановка функции (10) в уравнение (9) с учётом (11) дает:
<img src="http://ic3.static.km.ru/img/61658
Сокращая все члены этого уравнения на общий множитель e-i(E/ħ)t и произведя соответствующие преобразования, получим дифференциальное уравнение, определяющее функцию ψ:
<img src="http://ic3.static.km.ru/img/61658
Если функция U зависит от времени явно, то и решение последнего уравнения – функция ψ – будет зависеть от времени, что противоречит предположению (10).
Уравнение (12) называется уравнением Шрёдингера для стационарных состояний (или уравнением Шрёдингера без времени).
К уравнению Шрёдингера можно прийти и следующим путем следующих рассуждений. Из опытов по дифракции микрочастиц вытекает, что параллельный пучок частиц обладает свойствами плоской волны, распространяющейся в направлении движения частиц. Уравнение плоской волны, распространяющейся в направлении оси x, имеет, как известно, вид:
<img src="http://ic3.static.km.ru/img/61658
Это выражение часто пишут в комплексном виде:
<img src="http://ic3.static.km.ru/img/61658
подразумевая, что надо принимать во внимание вещественную часть этого выражения.
Согласно гипотезе де Бройля свободному движению частицы соответствует плоская волна с частотой ω=Е/ħ и длиной волны λ = 2πħ/р. Заменяя ω и λ в выражении (13) соответствующими выражениями, получим волновую функцию для свободной частицы, движущейся в направлении оси х:
<img src="http://ic3.static.km.ru/img/61658
Чтобы найти дифференциальное уравнение, которому удовлетворяет функция (14), воспользуемся соотношением между Е и p:
Продифференцировав функцию (14) один раз по t, a второй раз дважды по x, получим:
<img src="http://ic3.static.km.ru/img/61658
Из этих соотношений можно выразить Е и р2 через функцию Ψ и ее производные:
<img src="http://ic3.static.km.ru/img/61658
Как видим прослеживается полная аналогия с (7*). Подставляя полученные выражения в соотношение (15) получим дифференциальное уравнение:
<img src="http://ic3.static.km.ru/img/61658
Если направление волны не совпадает с осью х (или у, или z), фаза колебаний будет зависеть от всех координат: х, у и z. В этом случае дифференциальное уравнение имеет вид:
<img src="http://ic3.static.km.ru/img/61658
Полученное уравнение совпадает с уравнением Шрёдингера (8) (частица по условию свободна, U=0). Подстановка (10) в это уравнение (такая подстановка правомерна, так как U = 0, т. е. не зависит от t) приводит к уравнению Шрёдингера для стационарных состояний:
<img src="http://ic3.static.km.ru/img/61658
Это уравнение совпадает с уравнением (12) для случая U = 0.
Таким образом, мы получили уравнение Шрёдингера для свободно движущейся частицы. Теперь следует обобщить уравнение (16) на случай частицы, движущейся в потенциальном поле сил, когда полная энергия Е слагается из кинетической энергии Т и потенциальной энергии U.
В случае свободной частицы полная энергия Е совпадает с кинетической Т, так что величину Е в уравнении (16) можно трактовать либо как полную, либо как кинетическую энергию частицы. Обобщая уравнение (16) на случай движения частицы в поле сил, нужно решить вопрос о том, что следует подразумевать для такой частицы под величиной Е: полную или только кинетическую энергию. Если принять, что Е – полная энергия частицы, обобщенное уравнение, определяющее ψ, а значит, и сама ψ не будет зависеть от вида функции U, т. е. от характера силового поля. Это, очевидно, не может соответствовать действительному положению вещей. Поэтому следует признать, что при наличии сил, действующих на частицу, вместо Е в уравнение (16) нужно ввести кинетическую энергию частицы Т = Е –U. Произведя такую замену, мы придем к уравнению (12).
Приведенные нами рассуждения не могут рассматриваться как вывод уравнения Шрёдингера. Их цель — пояснить, каким образом можно было прийти к установлению вида волнового уравнения для микрочастицы. Доказательством же правильности уравнения Шрёдингера может служить лишь согласие с опытом тех результатов, которые получаются с помощью этого уравнения.
Основные свойства уравнения Шрёдингера
Условия, которым должны удовлетворять решения уравнения Шрёдингера, имеют весьма общий характер. Прежде всего волновая функция должна быть однозначной и непрерывной во всем пространстве. Требование непрерывности сохраняется и в тех случаях, когда само поле
U (х, у, z) имеет поверхности разрыва. На такой поверхности должны оставаться непрерывными как волновая функция, так и ее производные. Непрерывность последних, однако, не имеет места, если за некоторой поверхностью потенциальная энергия U обращается в бесконечность. В область пространства, где U = ∞, частица вообще не может проникнуть, т. е. в этой области должно быть везде ψ = 0. Непрерывность ψ требует, чтобы на границе этой области ψ обращалось в нуль; производные же от ψ в этом случае испытывают, вообще говоря, скачок.
Вид волнового уравнения физической системы определяется ее гамильтонианом, приобретающим в силу этого фундаментальное значение во всем математическом аппарате квантовой механики.
Вид гамильтониана свободной частицы устанавливается уже общими требованиями, связанными с однородностью и изотропией пространства и принципом относительности Галилея. В классической механике эти требования приводят к квадратичной зависимости энергии частицы от ее импульса: Е = р2/2т, где постоянная т называется массой частицы. В квантовой механике те же требования приводят к такому же соотношению для собственных значений энергии и импульса – одновременно измеримых сохраняющихся (для свободной частицы) величин.
Но для того чтобы соотношение Е = р2/2т имело место для всех собственных значений энергии и импульса, оно должно быть справедливым и для их операторов:
<img src="http://ic3.static.km.ru/img/61658
Подставив сюда оператор импульса <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/61658
069.gif» />, получим гамильтониан свободно движущейся
<img src="http://ic3.static.km.ru/img/61658
где Δ= д2/дх2 + д2/ду2 + д2/дz2 — оператор Лапласа.
В классической (нерелятивистской) механике взаимодействие с внешним полем описывается аддитивным членом в функции Гамильтона – потенциальной энергией взаимодействия U. являющейся функцией координат. Прибавлением такой же функции к гамильтониану системы описывается и взаимодействие в квантовой механике – гамильтониан для частицы, находящейся во внешнем поле:
<img src="http://ic3.static.km.ru/img/61658
где U(x,y,z) – потенциальная энергия частицы во внешнем поле.
Если поле U (х, у, г) нигде не обращается в бесконечность, то волновая функция тоже должна быть конечной во всем пространстве. Это же условие должно соблюдаться и в тех случаях, когда U обращается в некоторой точке в бесконечность, но не слишком быстро — как l/rs с s 0. Имея также в виду очевидное неравенство Ū > Umin, найдем, что и Ē > Umln . Поскольку это неравенство имеет место для любого состояния, то ясно, что оно справедливо и для всех собственных значений энергии:
Рассмотрим частицу, движущуюся в силовом поле, исчезающем на бесконечности; функцию U(х, у, z), как обычно принято, определим так, чтобы на бесконечности она обращалась в нуль. Легко видеть, что спектр отрицательных собственных значений энергии будет тогда дискретным, т. е. все состояния с Е 0 уравнение Шрёдингера, вообще говоря, не имеет (в рассматриваемом поле) решений, для которых бы интеграл <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/61658
Обратим внимание на то, что в квантовой механике при финитном движении частица может находиться и в тех областях пространства, в которых Е Е. В классической механике невозможность проникновения в эту область связана с тем, что при Е 0 (причем на бесконечности U → 0), то в силу неравенства (19) имеем Еп > 0. Поскольку, с другой стороны, при Е > 0 спектр должен быть непрерывным, то мы заключаем, что в рассматриваемом случае дискретный спектр вообще отсутствует, т. е. возможно только инфинитное движение частицы.
Предположим, что U в некоторой точке (которую выберем в качестве начала координат)
обращается в – ∞ по закону
Рассмотрим волновую функцию, конечную в некоторой малой области (радиуса r0) вокруг начала координат и равную нулю вне ее. Неопределенность в значениях координат частицы в таком волновом пакете порядка r0 ; поэтому неопределенность в значении импульса
ħ/r0. Среднее значение кинетической энергии в этом состоянии порядка величины ħ2/ <img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/61658
081.gif» />, а среднее значение потенциальной энергии
– α /<img style="float: left; margin: 0 10px 5px 0;" src="http://ic3.static.km.ru/img/61658
083.gif» />. Предположим сначала, что s > 2.
<img src="http://ic3.static.km.ru/img/61658
при достаточно малых r0 принимает сколь угодно большие по абсолютной величине отрицательные значения. Но если средняя энергия может принимать такие значения, то это во всяком случае означает, что существуют отрицательные собственные значения энергии, сколь угодно большие по абсолютной величине. Уровням энергии с большим |Е| соответствует движение частицы в очень малой области пространства вокруг начала координат. «Нормальное» состояние будет соответствовать частице, находящейся в самом начале координат, т. е. произой-дет «падение» частицы в точку r = 0.
Если же s Е, волновые функции быстро затухают). Таким образом, в рассматриваемом случае дискретный спектр содержит бесконечное множество уровней, которые сгущаются по направлению к уровню Е = 0.
Если же на бесконечности поле спадает, как – 1/rs с s > 2, то сколь угодно малых по абсолютной величине отрицательных уровней нет. Дискретный спектр кончается уровнем с отличным от нуля абсолютным значением, так что общее число уровней конечно.
Уравнение Шрёдингера для волновых функций ψ стационарных состояний, как и накладываемые на его решения условия, – вещественно. Поэтому его решения всегда могут быть выбраны вещественными (хотя это не справедливо для систем, находящихся в магнитном поле). Что касается собственных функций невырожденных значений энергии, то они автоматически оказываются вещественными с точностью до несущественного фазового множителя. В самом деле, ψ* удовлетворяет тому же уравнению, что и ψ, и потому тоже есть собственная функция для того же значения энергии; поэтому если это значение не вырождено, то ψ и ψ* должны быть по существу одинаковыми, т. е. могут отличаться лишь постоянным множителем (с модулем, равным единице). Волновые же функции, соответствующие одному и тому же вырожденному уровню энергии, не обязательно вещественны, но путем соответствующего выбора их линейных комбинаций всегда можно получить набор вещественных функций.
Полные же (зависящие от времени) волновые функции Ψ определяются уравнением, в коэффициенты которого входит i. Это уравнение, однако, сохраняет свой вид, если в нем заменить i на – i и одновременно перейти к комплексно сопряженному. Поэтому можно всегда выбрать функции Ψ такими, чтобы Ψ и Ψ* отличались только знаком у времени.
Как известно, уравнения классической механики не меняются при обращении времени, т. е. при изменении его знака. В квантовой механике симметрия по отношению к обоим направлениям времени выражается, как мы видим, в неизменности волнового уравнения при изменении знака i и одновременной замене Ψ на Ψ*. Надо, однако, помнить, что эта симметрия относится здесь только к уравнениям, но не к самому понятию измерения, играющему фундаментальную роль в квантовой механике.
5. О квантово-механическом представлении движения микрочастиц
Квантовая механика не позволяет определить местонахождение частицы в пространстве или траекторию, по которой движется частица. С помощью волновой функции можно лишь предсказать, с какой вероятностью частица может быть обнаружена в различных точках пространства. На первый взгляд может показаться, что квантовая механика дает значительно менее точное и исчерпывающее описание движения частицы, чем классическая механика, которая определяет «точно» местоположение и скорость частицы в каждый момент времени. Однако в действительности это не так. Квантовая механика гораздо глубже вскрывает истинное поведение микрочастиц. Она лишь не определяет того, чего нет на самом деле. В применении к микрочастицам понятия определенного местоположения и траектории вообще теряют смысл. Движение по определенной траектории несовместимо с волновыми свойствами, что становится совершенно очевидным, если проанализировать существо опытов по дифракции.
<img src="http://ic3.static.km.ru/img/61658
Рассмотрим дифракцию от двух близко расположенных отверстий (рис. 1). Вследствие интерференции волн, распространяющихся от отверстий, дифракционная картина не будет тождественна наложению дифракционных картин, получающихся от каждого из отверстий в отдельности (картина, получающаяся в случае рис. 1, а, не совпадает с наложением картин, получающихся в случаях б и в). Следовательно, вероятность попадания электрона (или какой-либо другой микрочастицы) в различные точки экрана при прохождении пучка через оба отверстия также не будет равна сумме вероятностей для случаев прохождения пучка через каждое из отверстий в отдельности. Отсюда неизбежно следует вывод, что на характер движения каждого электрона оказывают влияние оба отверстия. Такой вывод не совместим с представлением о траекториях. Если бы электрон в каждый момент времени находился в определенной точке пространства и двигался по траектории, он проходил бы через определенное отверстие — первое или второе. Явление же дифракции доказывает, что в прохождении каждого электрона участвуют оба отверстия – и первое, и второе.
Не следует, однако, представлять дело так, что какая-то часть электрона проходит через одно отверстие, а другая часть – через второе. Электрон, как и другие микрочастицы, всегда обнаруживается как целое, с присущей ему массой, зарядом и другими характерными для него величинами. Таким образом, электрон, протон, атомное ядро представляют собой частицы с весьма своеобразными свойствами. Обычный шарик, даже и очень малых размеров (макроскопическая частица), не может служить прообразом микрочастицы. С уменьшением размеров начинают проявляться качественно новые свойства, не обнаруживающиеся у макротел.
В ряде случаев утверждение об отсутствии траекторий у микрочастиц, казалось бы, противоречит опытным фактам. Так, например, в камере Вильсона путь, по которому движется микрочастица, обнаруживается в виде узких следов (треков), образованных капельками тумана; движение электронов в электроннолучевой трубке превосходно рассчитывается по классическим законам, и т. п. Это кажущееся противоречие объясняется тем, что при известных условиях понятия траектории и определенного местоположения оказываются применимыми к микрочастицам, но только с некоторой степенью точности.
Положение оказывается опять-таки точно таким, как и в оптике. Если размеры преград или отверстий велики по сравнению с длиной волны, распространение света происходит как бы вдоль определенных лучей (траекторий). При определенных условиях понятия положения в пространстве и траектории оказываются приближенно применимыми к движению микрочастиц, подобно тому, как оказывается справедливым закон прямолинейного распространения света.
Данный реферат не ставит перед собой цели полного описания уравнения Шрёдингера.
Значение уравнения Шрёдингера далеко не исчерпывается тем, что с его помощью можно найти вероятность нахождения частицы в различных точках пространства. Из этого уравнения и из условий, налагаемых на волновую функцию, непосредственно вытекают правила квантования энергии.
Условия состоят в том, что волновая функция ψ в соответствии с ее физическим смыслом должна быть однозначной, конечной и непрерывной во всей области изменения переменных х, у и z. В уравнение Шрёдингера входит в качестве параметра полная энергия частицы Е. В теории дифференциальных уравнений доказывается, что уравнения такого вида, как уравнение Шрёдингера, имеют решения, удовлетворяющие сформулированным выше условиям (т. е. однозначные, конечные и непрерывные), не при любых значениях параметра Е, а лишь при некоторых избранных значениях. Эти избранные значения называются собственными значениями параметра, а соответствующие им решения уравнения – собственными функциями задачи. Эти решения определяют принцип квантования энергии.
В общем можно заключить, что уравнение Шрёдингера (9) справедливо для любой частицы со спином равным 0, двигающейся со скоростью, малой по сравнению со скоростью света в вакууме (v Список литературы
Д. В. Сивухин Общий курс физики. Атомная и ядерная физика. Часть 1. – М.: «Наука», 1986 г.
Л. Д. Ландау и Е. М. Лифшиц. Теоретическая физика в десяти томах. Том III. Квантовая механика. Нерелятивистская теория. –М.: «Наука», 1989 г.
И. В. Савельев. Курс общей физики. Том III. Оптика, атомная физика, физика атомного ядра и элементарных частиц. – М.: «Наука», 1973 г.
Т. И. Трофимова. Курс физики. –М.: «Академия», 2004 г. Лекции по физике проф. С. Б. Раевского (НГТУ)
В. Г. Сербо и И. Б. Хриплович. Конспект лекций по квантовой механике. Учебное пособие. – Новосибирск, НГУ, 1999 г.
Р. Фейнман, Р. Лейтон, М. Сэндс. Фейнмановские лекции по физике Том 8. Квантовая механика (1). –М.: «Мир», 1966 г.
Г. П. Чуйко. Квантова Механiка. Конспективний навчальний курс квантовоï механiки. –Херсон, ХДПУ, 2000 г.
Лауреаты Нобелевской премии: Энциклопедия. Пер. с англ. — М.: «Прогресс», 1992.
Powered by FIST, NNSTU, 03-R-3 group, Alex V. Tertychnyi
🔍 Видео
Классические уравнения | уравнение Шрёдингера (координатное представление) | простейший выводСкачать

Классические уравнения | одномерное стационарное уравнение Шрёдингера | беск. потенц. яма | 1Скачать

Корректный вывод уравнения Шрёдингера и его физический смысл: Липовка А.А. - Глобальная волнаСкачать

Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

Лекция 12. Стационарные состояния.Уравнение Шредигера для стационарных состояний.Скачать

Лекция №4 "Волновая функция. Уравнение Шредингера" (Гавриков А.В.)Скачать

96. Уравнение ШредингераСкачать

Квантовая механика 41 - Уравнение Шредингера. Гамильтониан.Скачать

Стационарные состояния.Квантовая физикаСкачать

Классические уравнения | одномерное стационарное уравнение ШрёдингераСкачать

Структура материи 6: уравнение Шрёдингера. Зачем нужна квантовая механика – Виталий Бейлин | НаучпопСкачать

Урок 32. Уравнение ШрёдингераСкачать
Классические уравнения | трёхмерное стационарное уравнение ШрёдингераСкачать

Квантовая механика 47 - Стационарное уравнение Шредингера. Гармонический осциллятор.Скачать

Уравнение ШрёдингераСкачать

Урок 454. Понятие о волновой функцииСкачать

Лекция 5: Стационарное уравнение ШредингераСкачать

Рубцов А. Н. - Введение в квантовую физику - Волновая функция и уравнение ШредингераСкачать