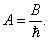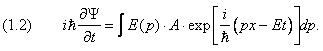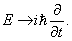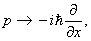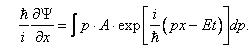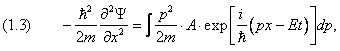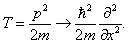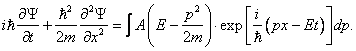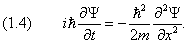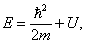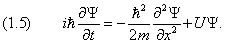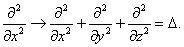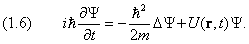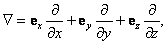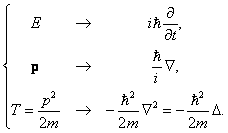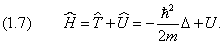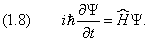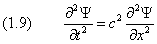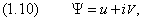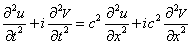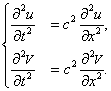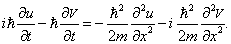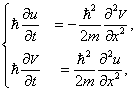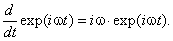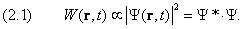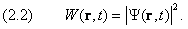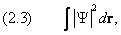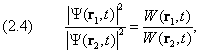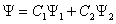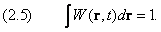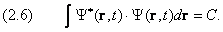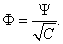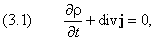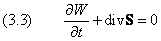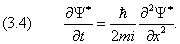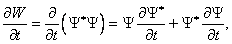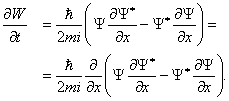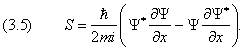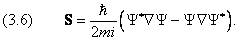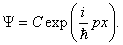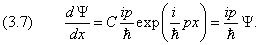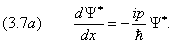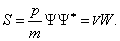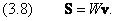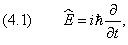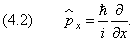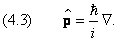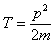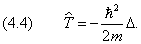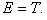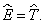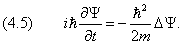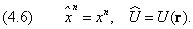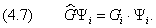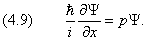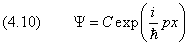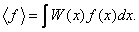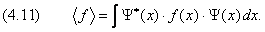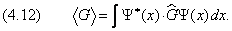Уравнение шредингера принцип суперпозиции в квантовой механике

Видео:Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

О коте Шредингера

Видео:Квантовая механика 13 - Принцип суперпозицииСкачать

Зачем

О ситуации с котом Шредингера, наверно, имеет представление большинство хабровцев, интересующихся физикой. Поэтому я не буду ее излагать. Дискуссия ведется вокруг интерпретации состояния кота. Вот альтернативы:

1. Кот “И жив И мертв”. Это описывается в квантовой механике как суперпозиция состояний “жив” и “мертв” и, значит, возможны какие-то интерференционные эффекты, подобно случаю рассеяния света на двух щелях.
2. Кот “ИЛИ жив ИЛИ мертв”. Эта трактовка запрещает вышеуказанную суперпозицию и, значит, запрещает интерференционные эффекты.

Моя задача изложить точку зрения, вытекающую, как мне кажется, из чтения книги “Квантовая механика” Фейнмана.

Видео:Урок 455. Уравнение ШрёдингераСкачать

Откуда ноги растут

А ноги растут из принципа суперпозиции. Он гласит:

Пусть система может находиться в состоянии $» data-tex=»inline»/>, в котором измерение наблюдаемой s дает всегда результат
и
пусть система может находиться в состоянии $» data-tex=»inline»/>, в котором измерение наблюдаемой s дает всегда результат ,
тогда систему можно приготовить и в суперпозиционном состоянии + c_2 |s_2> $» data-tex=»inline»/> где . В этом состоянии при измерении наблюдаемой s значение будет наблюдаться с вероятностью . Говорят, по-другому, что значение будет наблюдаться с амплитудой .

Принцип суперпозиции для двух состояний приводит к принципу суперпозиции для произвольного числа допустимых состояний системы для рассматриваемой наблюдаемой. Но нам важно только для двух состояний – живого и мертвого.

Заметим, как приготовить систему в суперпозиции – это другой вопрос. Вопрос технический. А принцип говорит, что можно приготовить суперпозицию. А как приготовить, он об этом ничего не говорит.

Суперпозиция ведет к интерференционным эффектам. И экспериментально она проявляется только в интерференции. Интерференция состояний — вот что отличает квантовую механику от классической. Интерференцию не всегда можно наблюдать. Ведь визуальная картина интерференции может меняться так быстро, что визуализирующий прибор с большим временем реакции отобразит усредненную картину, смазывающую или вообще ликвидирующую эффект интерференции. Но это уже дело техники. А вот при отсутствии суперпозиции никакая техника не обнаружит интерференции.

Большинство, наверно, знают отличие интерференционной картины от неинтерференционной при рассеянии на двух щелях. Вот картины этой интерференции (каждый квадратик – отдельная картинка):

Картины интерференции двух круговых когерентных волн, в зависимости от длины волны и расстояния между источниками.

Какие возможные интерференционные эффекты при суперпозиции живого и мертвого я не берусь описывать и, тем более, визуализировать их.

Видео:Структура материи 6: уравнение Шрёдингера. Зачем нужна квантовая механика – Виталий Бейлин | НаучпопСкачать

Примеры суперпозиции

Суперпозиция в обычном пространстве

Свободная частица описывается волновой функцией – волной де Бройля в координатном пространстве:

Здесь p – импульс, являющийся фиксированной величиной (параметр), а x – координата — переменная, которая может принимать любое значение координаты. Разные импульсы задают разные возможные состояния. Значит, возможна суперпозиция волн де Бройля, соответствующих различным импульсам. Это может быть конечная суперпозиция, счётная суперпозиция, континуальная суперпозиция, в которой сумма переходит в интеграл. Мы получим состояния, которое не обладает определенным значением импульса: при измерении импульса могут получаться различные значения и это не ошибка эксперимента.

Насколько обширен класс функций представимых такой суперпозицией? Вспоминая математику, мы узнаем в приведенных счетных суперпозициях ряд Фурье а в континуальной суперпозиции интеграл Фурье – Фурье разложение по p. Вот она таинственная связь абстрактной математики и конкретной физики! Обширными исследованиями матанализ описывает класс Фурье-разложимых функций. А для физики это просто суперпозиция плоских волн с различными импульсами.

Суперпозиция в импульсном пространстве

Симметрии ради можно аналогично рассмотреть волну де Бройля в импульсном пространстве — частицу с фиксированной координатой:

Здесь x – координата, являющаяся фиксированной величиной (параметр), а импульс p — переменная, которая может иметь любое значение импульса. Разные координаты задают разные возможные состояния. Значит, возможна суперпозиция волн де Бройля, соответствующих различным координатам. Это может быть конечная суперпозиция, счётная суперпозиция, континуальная суперпозиция, в которой сумма переходит в интеграл. Мы получим состояния, которое не обладает определенной координатой: при измерении координаты могут получаться различные значения и это не ошибка эксперимента.

Суперпозиция в энергетическом пространстве

Стационарное состояние – состояние с фиксированной энергией. Оно описывается волновой функцией – волной де Бройля в энергетическом пространстве:

Здесь e – энергия, являющаяся фиксированной величиной (параметр), а время t есть переменная, могущая принимать любое значение времени. Разные энергии задают разные возможные состояния. Значит, возможна суперпозиция волн де Бройля, соответствующих различным энергиям. Это суперпозиция стационарных состояний, которая может описывать нестационарные состояния — коэффициенты суперпозиции могут зависеть от времени.

Суперпозиция в спиновом пространстве

Фотон с круговой поляризацией представляется как суперпозиция двух линейных поляризаций.

Суперпозиция в пространстве фундаментальных частиц

Фотон как суперпозиция

В стандартной модели фотон является суперпозицией бозонов и .

Нейтрино как суперпозиция

Каждое нейтрино с определенной массой — суперпозиция электронного, мюонного и тау-нейтрино. И, обратно, электронное нейтрино, мюонное нейтрино и тау-нейтрино – суперпозиция трёх нейтрино с определёнными массами.

Каон как суперпозиция

Ситуация c каонами похожа на ситуацию с нейтрино.

Суперпозиция в пространстве жизни

Принцип суперпозиции не говорит о том, исчерпываются ли все состояния суперпозициями. Например, есть ли физические состояния, которые не представимы в виде суперпозиции плоских волн? — Я не знаю.

Цитата из Фейнмана:

Мы описали сейчас одно из величайших достижений теоретической физики. Оно не основано на элегантных математических трюках, подобных общей теории относительности, тем не менее полученные предсказания так же важны, как, например, предсказание позитрона. Особенно интересным является тот факт, что мы довели принцип суперпозиции до логического конца. Бом и его сотрудники полагали, что принципы квантовой механики не имеют фундаментального характера и, в конечном счете, не смогут объяснить новые явления. Однако эти принципы работают. Это еще не доказывает, что они верны, но я готов биться об заклад, что принцип суперпозиции будет стоять в веках!

Вопросы

Если мы имеем суперпозицию, то можно ли говорить, что система состоит из суперпозиционных составляющих? Белый свет состоит из радуги? Фотон состоит из бозонов? Что значит “состоит”? Можно функцию разложить в ряд Фурье по синусоидам, а можно разложить в ряд Фурье по полиномам Лежандра, по полиномам Чебышева и т.д. Так из чего она состоит? Всякая ли математическая суперпозиция осуществима физически? Саму синусоиду можно разложить в ряд Фурье по полиномам Лежандра. Значит, может существовать некий прибор, который разложит монохроматический свет по полиномам Лежандра. Значит можно говорить, что монохроматический свет состоит из “волн Лежандра”? Тогда можно ввести и понятие “фотон Лежандра”. И в каких-то ситуациях проще будет оперировать фотоном Лежандра, а не обычным синусоидальным фотоном. Можно представить себе радио на волнах Лежандра…

Похоже на то, что если мы обнаруживаем суперпозицию состояний, считавшихся ранее состояниям разных, несуперпозируемых систем, то эти состояния нужно считать состояниями, какой-то новой единой системы.

Переходим к коту Шредингера. Он может находиться в состоянии “жив” и может находиться в состоянии “мертв”. Значит, по принципу суперпозиции он может находиться и в суперпозиции состояний “жив” и “мертв”. Возможно не в текущей ситуации, но в какой-то другой обязательно. Так ли это? И какие возможные интерференционные эффекты можно наблюдать в этом случае?
А давайте обобщим кота: перейдем к понятию “животное”. Мы знаем, что оно может находиться в состояниях лев, человек,… Значит по принципу суперпозиции возможна и их суперпозиция. Это абсурд. Идем дальше и “животное” обобщим до понятия “материальный объект”. Тогда нужно допустить суперпозицию любых материальных объектов. Этот еще больший абсурд. Похоже, что нужно уточнить понятие системы. Видимо, нужно брать конкретную систему (конкретный кот), а не абстрактную (животное). Но ведь предложил же Гейзенберг рассматривать протон и нейтрон как разные состояния системы “нуклон» и получил интересные следствия.

Видео:В чем парадокс ЭФФЕКТА НАБЛЮДАТЕЛЯ? | Кот Шрёдингера и параллельные мирыСкачать

Что говорит Фейнман

Обратимся к Фейнману. Он рассматривает эксперимент по рассеянию нейтронов на кристалле.

Я резюмирую текст Фейнмана так.

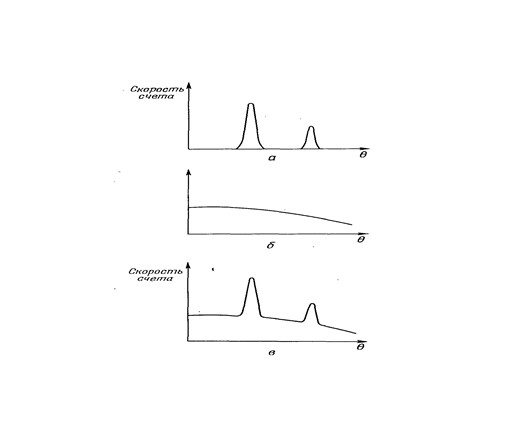
После рассеяния нейтронов на кристалле на выходе есть две системы нейтронов:

1. Упруго рассеянные нейтроны
2. Неупруго рассеянные нейтроны, имеющие перевернутый спин по сравнению с первоначальным

Суперпозиции между первой и второй системами нет. Они физически различимы. В первой системе нейтроны суперпозируют и получается типичная интерференционная картина a). На нее накладывается картина б) сложения интенсивностей во второй системе). Итоговый рисунок — в).

Суперпозиция во второй системе есть, а интерференции нет. Интерференцию разрушает случайность сдвига фаз при перевороте спина. То, что это так показывает интерференция двух специально приготовленных нейтронных пучков с разными ориентациями спина, в том числе и с противоположно направленными спинами. Интерференция есть при достаточной когерентности пучков. Более того, обнаружен эффект безумный с точки зрения здравого смысла. Если во втором пучке нейтроны имеют спин, повернутый на 360 градусов по сравнению со спином первого пучка, то наблюдается максимальная интерференция. Это не лезет ни в какие ворота. Поворот на 360 градусов не привел к первоначальному состоянию. Объяснить это невозможно. Однако с формальной точки зрения здесь все понятно. Нейтрон описывается спинором, а не скаляром как скалярный мезон, или вектором как фотон. Квантовая механика допускает амплитуды, описываемые спинорами — величинами, совпадающие с собой только при двойном обороте — повороте на 720 градусов. А поворот на один оборот может сопровождаться умножением амплитуды на комплексное число с модулем 1. Физика спинора при этом не изменится – средние не изменятся. Но при наложении пучков возможны эффекты интерференции. Отсюда и происходит указанный интерференционный эффект.

Видео:Консультация по квантовой механике. Часть 5. "Волновая функция. Уравнение Шредингера"Скачать

Так что же может суперпозировать?

Ни в одном учебнике по квантовой механике, с которыми я знакомился, я не нашел критерия возможности суперпозиции. И только у Фейнмана я встретил рецепт при рассмотрении им рассеяния на двух щелях.

Критерий Фейнмана

Никогда не складывайте амплитуды разных, отличных друг от друга конечных состояний. Как только фотон был воспринят одним из фотонных счетчиков около щелей, мы всегда, если надо, можем узнать не возмущая больше системы, какая из альтернатив (взаимоисключающих событий) реализовалась. У каждой альтернативы есть своя вероятность, полностью независимая от другой. Повторяем, не складывайте амплитуд для различных конечных условий(под “конечным” мы понимаем тот момент, когда нас интересует вероятность, т.е. когда опыт “закончен”). Зато нужно складывать амплитуды для разных неразличимых альтернатив в ходе самого опыта, прежде чем целиком закончится сам процесс. В конце процесса вы можете, если хотите, сказать, что вы “не желаете смотреть на фотон”. Это ваше личное дело, но все же амплитуды складывать нельзя. Природа не знает, что вы на нее смотрите, и ей безразлично, интересуют ли вас ее данные или нет. Так что мы не должны складывать амплитуды.

Итак, если есть физически неразличимые пути достижения точки, в которой мы рассматриваем возможность интерференции, то амплитуды этих путей складываются и мы имеем интерференцию. Если они физически различимы, то складываются вероятности и, значит, интерференции нет. Под путем понимается движение не только в обычном пространстве. Так если есть две моды распада частицы с одним исходом, то они должны суперпозировать.

Назовем приведенные выше максимы Фейнмана суперпозиционным критерием Фейнмана.
Итак, Фейнман говорит, что суперпозировать могут только физически неразличимые траектории.

Высказывание Дирака

…каждый фотон интерферирует лишь с самим собой. Интерференции между двумя разными фотонами никогда не происходит.

Надо полагать это относится и к любому объекту. Поэтому и кот может интерферировать только с самим собой. Мертвый кот и живой кот – это предельно разные коты. Да и можно ли называть труп мертвым котом. Это труп кота, но никак не кот.

Сомнения

Что считать под системой в принципе суперпозиции? Если мы рассматриваем состояния с разным значением импульса электрона, то это, несомненно, разные состояния одной системы, называемой электрон. Если мы рассматриваем разные энергетические состояния атома водорода, то это также одна система — атом водорода. Но вот Гейзенберг предложил рассматривать протон и нейтрон как разные состояния нуклона. Тогда, что возможна суперпозиция протона и нейтрона? Но тогда почему невозможно суперпозиция электрона и позитрона? Говорят, что это противоречит закону сохранения электрического заряда. Тогда почему суперпозиция разных энергетических состояний не противоречит закону сохранения энергии? Энергию уносит фотон? Тогда и заряд может уносить рождающаяся частица. Можно объявить честно (Кемпфер, Липкин), что суперпозиций с разными электрическими зарядами не наблюдалось в природе, хотя такая суперпозиция не противоречит никаким законам.

О физической различимости траекторий системы. Что служит метками различимости? Точки пространства? – Нет. Точки времени? Заряды: масса, электрический, лептонный, барионый? Спин? Только внутренние характеристики? Фейнман говорит, что это отметки во внешней среде, которые можно обнаружить. При рассеянии нейтронов на кристалле нейтрон с перевернутым спином оставляет метку в кристалле – ядро с перевернутым спином. Любое неупругое рассеяние оставляет метку (энергетическую, спиновую…) в рассеивающей среде, а упругое нет. Значит при прохождении через щели интерферируют фотоны только упругого рассеяния.

В отношении различимости можно сказать еще вот что. Наше знание неточно, и то, что сегодня считается физически неразличимым, завтра может оказаться различимым. Так произошло с понятиями правый, левый. Если считать правое и левое чисто условностями, то эта условность не должна входить в фундаментальные формулы. Но вот оказалось, что для слабого взаимодействия понятия “правый”, “левый” отнюдь не условность: правое и левое состояния различаются слабыми взаимодействиями. И в лагранжиан слабого взаимодействии включили отдельно “правые” и “левые” члены. Т.е. не ответив на вопрос «почему правое отличается от левого?», тем не менее, успешно ответили на вопрос “как это происходит?” Это, впрочем, не ново. Еще Ньютон, на упреки в том, что он не объяснил природу тяготения, а просто привел формулу закона тяготения ответил примерно так, что да, я не знаю природы тяготения и не выдвигаю на этот счет никаких гипотез, зато я знаю, как описывается закон тяготения и это уже кое-что. Подобный подход вылился в некую философию: некоторые физики прямо заявляют, что дело физики выяснить “как?”, а не “почему?”. Ну, в самом деле, что ответить на вопрос «Почему справедливы уравнения Максвелла?”. Этого никто не знает.

Аналогично с ситуацией “правое-левое” произошло и в случае каонов. Казалось бы, есть два совершенно различимых типа каонов. Один распадается на два мезона. А второй на три. Но Гелл-Манн и Пайс предположили, что мы имеем дело с распадом одной частицы. А две моды распада возникают из-за того, что эта исходная частица представляет собой суперпозицию двух других типов каонов.

Все это так. Но, сомнительно, что когда-нибудь живой и мертвый кот объединятся в одну систему и различие между живым и мертвым станет эфемерным.

Видео:Параллельные миры, квантовая механика и кот [Veritasium]Скачать

Что не может суперпозировать?

Суперпозиция разных частиц

Представим себе эксперимент с двумя щелями, когда через одну щель проходит плоская волна электронов, а через другую плоская волна протонов. Пусть длины волн де Бройля постоянны и одинаковы. Будет ли наблюдаться интерференция? Если формально рассматривать, то волна протона описывается точно так же, как и волна электрона. И почему бы не быть интерференции? Но в квантовой теории поля волны будут одинаковы только в пространственной части. А неодинаковы они будут по заряду и спину. Но давайте останемся в рамках обычного рассмотрения опыта на щелях. Рассмотрим пучок электронов и отрицательных мюонов. Там и заряды и спины одинаковы. А будет ли интерференция? Ответ дает критерий Фейнмана. Раз частицы физически различимы, то интерференции не будет. Как в опыте с одинаковыми частицами, когда проверяется прохождение через щель, проверка делает частицы различимыми и интерференция исчезает, так при опыте с различными частицами они уже физически различимы изначально. Интерференции не будет. Обратно, если интерференция вроде бы одинаковых частиц, но от разных источников не наблюдается, то частицы различимы. Хотя эту различимость (характеристика, отвечающая за различимость) мы пока не обнаружили.

Суперпозиция мертвого и живого

В принципе суперпозиции говорится о состояниях определенной квантовой системы. Мертвый кот и живой кот – это совершенно разные физические системы. Cуперпозировать могут только физически неразличимые альтернативы. А мертвое и живое физически очень даже различимы. Можно даже сказать, что большей различимости, чем мертвое от живого и быть не может. Наше незнание о том, жив или мертв кот, возникает не вследствие суперпозиции, а вследствие нехватки информации, как в любой классической вероятностной задаче. А в случае суперпозиции, речи о нехватке информации нет и, как утверждает копенгагенская интерпретация квантовой механики, и быть не может.

Если эксперимент показывает отсутствие суперпозиции упруго рассеянного нейтрона и неупруго рассеянного нейтрона, то логично утверждать, что мертвый кот и живой не могут суперпозировать. Они фундаментально отличаются друг от друга.

Суперпозиция живого и живого

Живая система предполагает непрерывный обмен веществом и энергией с внешней средой. Этим она непрерывно метится – становится физически различимой. Значит, живое не может интерферировать. Оно не может застыть и оставаться идентичным. Живое все время неидентично само себе. Это все время другая система.

Итак, пользуясь критерием Фейнмана мы заключаем, что

1. Нейтрон с перевернутым спином и не перевернутым при рассеянии нейтронов на кристалле не суперпозируют
2. Частицы с разными зарядами не могут суперпозировать. Протон и нейтрон суперпозируют только если забыть про электрические заряды — при отключении электромагнитного взаимодействия. Реально этого не сделать. И значит в реальности могут наблюдаться только некие следы от возможной суперпозиции. Например, сечения рассеяния протон-протон, нейтрон-нейтрон, протон-нейтрон будут близкими настолько насколько электромагнитное взаимодействие слабее сильного.
3. Протон и электрон не могут суперпозировать
4. Молекулы разных веществ не могут суперпозировать

Сомнения

Однако, почему в суперсимметрии допускается суперпозиция кварка и лептона? Возможно, что суперпозиция относительна и то, что в одних условиях суперпозиции нет, не означает, что она невозможна в других ситуациях? Тогда принцип суперпозиции нужно дополнить описанием ситуации суперпозиции. Так в ситуации отключения электромагнитного поля возможна суперпозиция протона и нейтрона.

Видео:Квантовая физика для чайников!Скачать

Уравнение Шрёдингера

Дуальная корпускулярно-волновая природа квантовых частиц описывается дифференциальным уравнением.

Согласно фольклору, столь распространенному среди физиков, случилось это так: в 1926 году физик-теоретик по имени Эрвин Шрёдингер выступал на научном семинаре в Цюрихском университете. Он рассказывал о странных новых идеях, витающих в воздухе, о том, что объекты микромира часто ведут себя скорее как волны, нежели как частицы. Тут слова попросил пожилой преподаватель и сказал: «Шрёдингер, вы что, не видите, что всё это чушь? Или мы тут все не знаем, что волны — они на то и волны, чтобы описываться волновыми уравнениями?» Шрёдингер воспринял это как личную обиду и задался целью разработать волновое уравнение для описания частиц в рамках квантовой механики — и с блеском справился с этой задачей.

Тут необходимо сделать пояснение. В нашем обыденном мире энергия переносится двумя способами: материей при движении с места на место (например, едущим локомотивом или ветром) — в такой передаче энергии участвуют частицы — или волнами (например, радиоволнами, которые передаются мощными передатчиками и ловятся антеннами наших телевизоров). То есть в макромире, где живём мы с вами, все носители энергии строго подразделяются на два типа — корпускулярные (состоящие из материальных частиц) или волновые. При этом любая волна описывается особым типом уравнений — волновыми уравнениями. Все без исключения волны — волны океана, сейсмические волны горных пород, радиоволны из далеких галактик — описываются однотипными волновыми уравнениями. Это пояснение нужно для того, чтобы было понятно, что если мы хотим представить явления субатомного мира в терминах волн распределения вероятности (см. Квантовая механика), эти волны также должны описываться соответствующим волновым уравнением.

Шрёдингер применил к понятию волн вероятности классическое дифференциальное уравнение волновой функции и получил знаменитое уравнение, носящее его имя. Подобно тому как обычное уравнение волновой функции описывает распространение, например, ряби по поверхности воды, уравнение Шрёдингера описывает распространение волны вероятности нахождения частицы в заданной точке пространства. Пики этой волны (точки максимальной вероятности) показывают, в каком месте пространства скорее всего окажется частица. Хотя уравнение Шрёдингера относится к области высшей математики, оно настолько важно для понимания современной физики, что я его все-таки здесь приведу — в самой простой форме (так называемое «одномерное стационарное уравнение Шрёдингера»). Вышеупомянутая волновая функция распределения вероятности, обозначаемая греческой буквой ψ («пси»), является решением следующего дифференциального уравнения (ничего страшного, если оно вам не понятно; главное — примите на веру, что это уравнение свидетельствует о том, что вероятность ведёт себя как волна):

где x — расстояние, h — постоянная Планка, а m, E и U — соответственно масса, полная энергия и потенциальная энергия частицы.

Картина квантовых событий, которую дает нам уравнение Шрёдингера, заключается в том, что электроны и другие элементарные частицы ведут себя подобно волнам на поверхности океана. С течением времени пик волны (соответствующий месту, в котором скорее всего будет находиться электрон) смещается в пространстве в соответствии с описывающим эту волну уравнением. То есть то, что мы традиционно считали частицей, в квантовом мире ведёт себя во многом подобно волне.

Когда Шрёдингер впервые опубликовал свои результаты, в мире теоретической физики разразилась буря в стакане воды. Дело в том, что практически в то же время появилась работа современника Шрёдингера — Вернера Гейзенберга (см. Принцип неопределенности Гейзенберга), в которой автор выдвинул концепцию «матричной механики», где те же задачи квантовой механики решались в другой, более сложной с математической точки зрения матричной форме. Переполох был вызван тем, что ученые попросту испугались, не противоречат ли друг другу два в равной мере убедительных подхода к описанию микромира. Волнения были напрасны. Сам Шрёдингер в том же году доказал полную эквивалентность двух теорий — то есть из волнового уравнения следует матричное, и наоборот; результаты же получаются идентичными. Сегодня используется в основном версия Шрёдингера (иногда его теорию называют «волновой механикой»), так как его уравнение менее громоздкое и его легче преподавать.

Однако представить себе и принять, что нечто вроде электрона ведёт себя как волна, не так-то просто. В повседневной жизни мы сталкиваемся либо с частицей, либо с волной. Мяч — это частица, звук — это волна, и всё тут. В мире квантовой механики всё не так однозначно. На самом деле — и эксперименты это вскоре показали — в квантовом мире сущности отличаются от привычных нам объектов и обладают другими свойствами. Свет, который мы привыкли считать волной, иногда ведёт себя как частица (которая называется фотон), а частицы вроде электрона и протона могут вести себя как волны (см. Принцип дополнительности).

Эту проблему обычно называют двойственной или дуальной корпускулярно-волновой природой квантовых частиц, причем свойственна она, судя по всему, всем объектам субатомного мира (см. Теорема Белла). Мы должны понять, что в микромире наши обыденные интуитивные представления о том, какие формы может принимать материя и как она себя может вести, просто неприменимы. Сам факт, что мы используем волновое уравнение для описания движения того, что привыкли считать частицами, — яркое тому доказательство. Как уже отмечалось во Введении, в этом нет особого противоречия. Ведь у нас нет никаких веских оснований полагать, будто то, что мы наблюдаем в макромире, должно с точностью воспроизводиться на уровне микромира. И тем не менее дуальная природа элементарных частиц остается одним из самых непонятных и тревожащих аспектов квантовой механики для многих людей, и не будет преувеличением сказать, что все беды начались с Эрвина Шрёдингера.

Видео:Понимаете ли вы квантовую механику? #наука #физика #экспериментСкачать

Уравнение шредингера принцип суперпозиции в квантовой механике

Задачи атомной физики решаются методами квантовой теории, которая принципиально отличается от классической механики.

Решение задачи о движении тела макроскопических размеров основано на применении второго закона Ньютона. Если известны силы, действующие на тело, то сначала мы находим его ускорение, затем — траекторию, после чего — все параметры движения. Но в масштабах атомов понятие траектории теряет свой смысл. Своё значение сохраняют так называемые интегралы движения. К ним относятся, в первую очередь, энергия, импульс, момент вращения и чётность. В квантовой теории эти величины определяются сразу, минуя этап вычисления траектории.

В основе расчётов лежит уравнение Шредингера. Решив его, мы находим набор энергетических уровней, который реализуется в заданном потенциале, а также получаем информацию статистического характера о возможном положении частицы.

Видео:Лекция №4 "Волновая функция. Уравнение Шредингера" (Гавриков А.В.)Скачать

8.1. Уравнение Шредингера

Уравнение Шредингера, как законы Ньютона и уравнения Максвелла, вывести нельзя. Оно основано на анализе экспериментальных данных и в масштабах атомов описывает волновые свойства частиц. Покажем связь уравнения Шредингера с волновым пакетом. Для этого запишем уравнение волнового пакета:

где B — амплитуда. Будем считать, что величина B как функция k равна нулю при k Δ k и k > Δ k . Тогда областью интегрирования становится вся числовая ось. Вспоминая соотношения де Бройля-Эйнштейна (формулы (2.1) и (2.1а) первой главы), приходим к новой записи выражения для волнового пакета

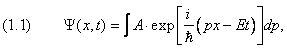
Продифференцируем (1.1) по времени:

Появлению энергии в подынтегральной функции соответствует оператор дифференцирования

Его называют оператором энергии . Импульс, в свою очередь, связан с оператором

в чём можно убедиться, дифференцируя (1.1) по x :

Мы рассматриваем нерелятивистскую частицу в отсутствие внешних полей, следовательно, ее энергия равна p2/2 m. Ей можно сопоставить оператор двойного дифференцирования по координате:

Вычитая (1.3) из (1.2), получим

Всё подынтегральное выражение вместе с разностью 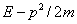равно нулю. Следовательно,

Мы вывели одномерное уравнение Шредингера для свободной частицы. Теперь учтём возможное присутствие внешних полей:

Здесь U = U( x , t ) — потенциальная энергия, зависящая только одной координаты. Вообще говоря, она может также меняться со временем. Соответственно, приходим к одномерному уравнению Шредингера:

Обобщение на случай трёх измерений сводится к замене производной по x оператором Лапласа:

Уравнение Шредингера с потенциалом, зависящим от всех трёх координат, имеет вид

Вектору импульса в трёхмерном случае соответствует оператор градиента:

где e _x , e _y и e _z — единичные векторы в направлении координатных осей. В процессе вывода мы использовали следующие соотношения между физическими величинами и операторами:

Оператор принято отмечать «шляпкой». Например, оператор, отвечающий физической величине G, обозначается как Ĝ. В квантовой механике вводится оператор энергии, или оператор Гамильтона

Он позволяет записать уравнение Шредингера следующим образом:

Уравнение Шредингера содержит мнимую единицу i , следовательно, его решение должно быть комплексным. Этим оно отличается от волнового уравнения в классической механике . В качестве примера рассмотрим одномерный случай. Классическое уравнение

позволяет работать отдельно с действительной и мнимой частями Y , каждая из которых подчиняется одному и тому же уравнению. В самом деле, если

где u и V — действительные функции, то уравнению (1.9), которое мы теперь запишем в виде

равносильна система одинаковых уравнений, каждое из которых совпадает с исходным :

Действительная и мнимая части Y разделились. Мы убедились, что в классическом случае нет принципиальной необходимости в комплексном представлении (хотя оно часто используется для удобства вычислений). Для уравнения Шредингера это не так. Разложение (1.10) вставим теперь в уравнение (1.4):

Этому уравнению эквивалентна система

в которой переменные u и V связаны друг с другом.

Структура уравнения Шредингера

показывает, что оно отображает закон сохранения энергии.

Уравнение Шредингера определяет зависимость волновой функции от времени и от координат. Как второй закон Ньютона описывает траекторию частицы, так уравнение Шредингера описывает эволюцию волновой функции.

Выход в комплексную плоскость является следствием требования, чтобы волновая функция в любой момент времени полностью определялась её начальным значением. Следовательно, уравнение Шредингера должно содержать только первую производную волновой функции по времени, но не вторую. Если ограничиться гармоническими функциями в действительной области, то волновое уравнение обязано содержать вторую производную. В самом деле, однократное дифференцирование переводит синус в косинус и наоборот. Но колебания могут быть описаны экспонентой с комплексным показателем. Её важное свойство заключается в том, что первая производная функции возвращает нас к ней самой:

Перейдём к обсуждению физического смысла волновой функции.

Видео:Простым Языком #1 Кот ШредингераСкачать

2.1. Волновая функция

Выкладки предыдущего раздела мы проводили, используя представление классической механики о волновом пакете. В уравнении Шредингера функция Y ( r , t ) приобретает новый смысл. Она называется волновой функцией и описывает уже не суперпозицию колебаний, но состояние реальной частицы. Перечислим основные свойства волновой функции.

Волновая функция как вероятность

В квантовой механике вся информация о частице содержится в её волновой функции. С учётом соотношения неопределённостей, эта информация носит вероятностный характер. А именно, квадрат модуля волновой функции пропорционален вероятности W найти частицу в данной точке в заданный момент времени:

Здесь звёздочка означает комплексное сопряжение. В большинстве задач, которые нам встретятся в дальнейшем, имеет место точное равенство:

Выбор между (2.1) и (2.2) определяется степенью локализации частицы в пространстве. Если вероятность найти частицу в удалённых точках исчезающе мала, то интеграл

взятый по всему пространству, сходится. В конечном итоге именно это и делает возможным равенство (2.2). Наоборот, свободно движущаяся частица может быть обнаружена в любой точке. Интеграл (2.3) для её волновой функции расходится и, следовательно, | Y | 2 не может служить вероятностью никакой величины. В этом случае справедливо отношение

которое является следствием (2.1). Ниже нам неоднократно будут встречаться волновые функции, модуль которых не стремится к нулю при удалении от начала координат, либо убывает слишком медленно. Хотя для таких функций не имеет смысла (2.2), тем не менее, отношение значений W в двух разных точках пространства равно отношению вероятностей обнаружить там частицу.

Принцип суперпозиции

Уравнение Шредингера линейно относительно волновой функции. Следовательно, любая линейная комбинация

его решений Y ₁ и Y ₂ также является его решением.

Таким образом, линейная комбинация волновых функций обязательно описывает некоторое состояние частицы (или системы частиц). В частности, при C₂ = 0 получаем, что решение уравнения Шредингера, известно с точностью до постоянного множителя.

Нормировка

Вероятность W по своему смыслу должна удовлетворять условию нормировки

Если частица совершает своё движение в ограниченной области, то, согласно предыдущему разделу, существует интеграл:

При выполнении последнего равенства волновая функция может быть преобразована так, чтобы условие

имело место даже в том случае, когда константа C не равна единице. А именно, условию (2.7) удовлетворяет функция

Согласно сказанному в предыдущем разделе, обе эти функции описывают одно и то же состояние. Процесс перехода от Y к F называется нормировкой, а функция F — норми p ованной волновой функцией.

Видео:Квантовая механика 41 - Уравнение Шредингера. Гамильтониан.Скачать

8.3 Ток вероятности

В газодинамике известно уравнение непрерывности для потока вещества

где r — плотность, а

поток вещества, движущегося со скоростью v . Оно справедливо в том случае, если нет источников и стоков частиц. Аналогичное соотношение

можно вывести и для плотности вероятности W . Сначала проведём расчёты для одномерного случая. Для определения вектора тока вероятности S воспользуемся уравнением Шредингера (1.4) для свободной частицы. Запишем его также для комплексно–сопряжённой волновой функции:

то, подставляя сюда выражения (1.4) и (3.4) для производных по времени от Y и Y *, находим

Последнее уравнение представляет собой аналог одномерного уравнения непрерывности, если поток вероятности принять равным

Обобщение на случай трёх измерений даёт уравнение непрерывности (3.3) с дивергенцией вектора

Физический смысл определённого таким образом потока вероятности S можно выяснить, вычислив его для свободной частицы, то есть, для волновой функции вида

Производная 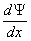выражается через Y :

Аналогично вычисляем производную от комплексно сопряжённой функции:

Подставляя (3.7) и (3.7а) в (3.5), получаем

Нетрудно убедиться, что в трёхмерном случае мы приходим к формуле

Она полностью аналогична (3.2), где роль плотности выполняет плотность вероятности W, а вместо потока массы j надо подставить вектор S.

Поток вероятности равен нулю в случае действительной волновой функции. Следовательно, последняя описывает финитное движение, то есть, движение в ограниченной области пространства.

Видео:Что такое квантовая суперпозиция?Скачать

8.4 Операторы физических величин

В этом разделе мы соберём вместе явные выражения для самых важных для нас операторов. Оператор энергии сводится к дифференцированию по времени:

а оператор проекции импульса на одну из координат — к дифференцированию по этой координате:

Аналогичные формулы справедливы для проекций момента на две другие оси, а в трёхмерном случае

вектор импульса выражается через оператор градиента:

При формировании операторов можно пользоваться соотношениями между классическими величинами. Так, оператор кинетической энергии 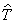с помощью соотношения

выражается посредством оператора Лапласа:

В отсутствие внешних полей полная энергия частицы равна её кинетической энергии:

В квантовой механике этому факту соответствует уравнение Шредингера для свободной частицы:

Последняя формула является обобщением (1.4) на случай трёх измерений.

Оператор координаты сводится к простому умножению на эту координату. То же самое справедливо и для оператора, представляющего любую функцию координат. Например,

В последующих разделах мы познакомимся с оператором момента вращения.

С математической точки зрения уравнения квантовой механики сводятся к линейной задаче на собственные значения с заданными граничными условиями.

Здесь Y _i — собственные функции, а G _i — собственные значения оператора 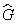. Физический смысл (4.7) заключается в следующем. В результате измерения можно обнаружить только те значения физической величины, которые входят в спектр собственных значений её оператора.

Спектр собственных значений может быть как дискретным, так и непрерывным. Например, непрерывным является спектр импульса свободной частицы. Покажем это для одномерного случая. Вычислим собственное значение p проекции импульса на ось x :

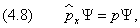
Решение последнего уравнения

в комплексной форме выражает «мгновенную фотографию» плоской монохроматической волны, распространяющейся вдоль оси x . Не удивительно, что мы получили именно такое решение, так как мы исходили из представления плоских волн при получении уравнения Шредингера. Временнýю часть волновой функции мы установим позже.

Отметим важную особенность функции (4.10): квадрат её модуля равен константе |C| 2 . Следовательно, свободно летящая частица с равной вероятностью может находиться в любой точке пространства. Как уже было сказано в разделе (2.1), такую функцию невозможно нормировать приведённым там способом. Таким образом, она представляет собой пример волновой функции, квадрат модуля которой пропорционален вероятности в смысле (2.4), но не имеет места (2.1).

Среднее значение.

В этом разделе мы с самого начала предполагаем, что волновая функция квадратично интегрируема, то есть существует интеграл (2.6). Как известно из математики, среднее значение 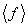функции координат f ( x ) определяется с помощью вероятности W( x ) как

Для операторов, зависящих только от координат, это определение без всяких изменений переносится в квантовую механику. Нужно только вместо вероятности написать квадрат модуля волновой функции:

Здесь интегрирование ведётся по всей области изменения аргумента x .

В общем случае, когда физическая величина G не является функцией координат (например, импульс), её среднее значение определяется как

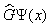
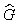
Подынтегральная функция состоит из двух сомножителей: Y * ( x ) и — результата воздействия оператора на функцию Y ( x ). Формула (4.11) является частным случаем (4.12), когда

Пусть система находится в определённом состоянии, соответствующем собственному значению G _i и собственному вектору — волновой функции Y _i . Если физическую величину G усреднять с помощью функции Y _i , то среднее значение 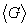равно G _i . В этом легко убедиться, подставив (4.7) в (4.12).

📽️ Видео

▽ Квантовая запутанность(что такое квантовая запутанность)Скачать

Шрёдингер и его уравнение — Дэвид Клэри / ПостНаукаСкачать

Классические уравнения | уравнение Шрёдингера (координатное представление) | простейший выводСкачать

Странные квантовые дела #2 [Суперпозиция и запутанность]Скачать

Квантовая физика простым языком - поймут всеСкачать

КВАНТОВАЯ ЗАПУТАННОСТЬ ИЛИ ЗА ЧТО ВРУЧИЛИ НОБЕЛЕВСКУЮ ПРЕМИЮ?Скачать

Лекция №04 "Уравнение Шредингера"Скачать