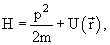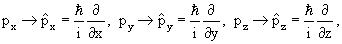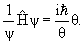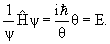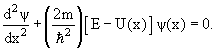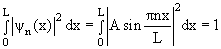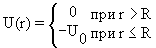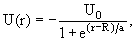Планетарная модель водородоподобного атома, сформулированная Бором, не является ни классической (поскольку допускает квантование), ни квантовой (поскольку квантование не объясняет). Объяснить квантование можно с помощью уравнения Шредингера.
Однако описание атомов и молекул с помощью уравнения Шредингера является сложной задачей. Это касается даже простейшего атома водорода и водородоподобных ионов. Поэтому ограничимся здесь качественным рассмотрением задачи, которая сводится к анализу движения электрона в кулоновском иоле ядра. Потенциальная энергия взаимодействия электрона с ядром заряда Ze задается формулой
Здесь г — расстояние между электроном и ядром. Необходимо учитывать, что атом принципиально является трехмерной системой, и одномерным приближением для его описания обойтись нельзя. Поэтому стационарное уравнение Шредингера для водородоподобного атома записывается следующим образом:
Масса ядра на несколько порядков больше массы электрона, поэтому систему центра масс обычно можно считать привязанной к ядру. Поле, в котором движется электрон, является в этой системе центрально-симметричным.
Задачи такой геометрии удобно решать в сферической системе координат (рис. 37.1). В ней для точки М выбраны координаты г, 0, ср. Расстояние до начала координат г равно ОМ. Полярный (зенитный) угол 0 — это угол между осью Oz и радиус- вектором г, который меняется в пределах от 0 до к. Азимутальный угол ф — это угол между осью Ох и проекцией радиус-вектора г на плоскость Оху, ко- Рис.37.1 торый меняется в пределах от 0 до 2л. Переход
к сферической системе от декартовой и обратно осуществляется по следующим из геометрии правилам:
После перехода к сферической системе координат решение уравнения Шредингера ищется в виде произведения трех составляющих, каждая из которых зависит от одной из сферических координат:
Решение уравнения Шредингера с трехмерным кулоновским потенциалом оказывается еще более сложным, чем в предыдущей задаче с одномерным потенциалом гармонического осциллятора. Аналогично предыдущим квантовым задачам поиск собственных волновых функций (с учетом естественных ограничений) приводит к получению дискретных собственных энергетических состояний. И каждая из составляющих волновой функции дает набор решений, характеризующийся своим квантовым числом: главным п, орбитальным / и магнитным т,.
- Уравнение Шредингера
- Предпосылки вывода уравнения Шредингера
- Готовые работы на аналогичную тему
- Общий вид уравнения Шредингера
- Уравнение Шредингера на примере атома водорода
- Уравнение шредингера для стационарных состояний электрона находящегося в атоме водорода
- 4.1. Уравнение Шредингера
- Уравнение Шредингера
- 4.2. Частица в одномерной прямоугольной яме с бесконечными стенками
- 4.3. Гармонический осциллятор
- Частица в одномерной потенциальной яме
- 4.4. Частица в поле с центральной симметрией
- 4.5. Орбитальный момент количества движения
- 4.6. Спин
- 4.7. Полный момент количества движения
- 4.8. Квантовые числа
- Таблица квантовых чисел
- Задачи
- 🎬 Видео
Видео:Лучшая модель атома? [Минутка физики]Скачать
![Лучшая модель атома? [Минутка физики]](https://i.ytimg.com/vi/eybcxXiYJfc/0.jpg)
Уравнение Шредингера
Вы будете перенаправлены на Автор24
Видео:Урок 455. Уравнение ШрёдингераСкачать

Предпосылки вывода уравнения Шредингера
Основная идея волновой механики заключается в том, что для таких малых тел, как электрон, нельзя с определенностью сказать, где оно находится в данное время и куда направляется. Можно установить только относительную вероятность его нахождения в том или ином месте и наличие определенного количества движения в определенный момент времени.
В соответствии с волновой механикой какая-либо система – атом, молекула, электрон и т.д. – описывается функцией состояния или волновой функцией, обозначаемой $psi$ («пси»), которая является функцией координат всех частиц, образующих эту систему. Следовательно, величина $psi$ зависит только от положения всех частиц в пространстве.
В 1924 г. де Бройль предположил, что точно также, как свет, который, как обычно считают, имеет волновую природу, на самом деле при определенных обстоятельствах ведет себя, как будто он состоит из частиц – квантов, — так и очень малые частицы, такие, как электроны, также могут обладать волновыми свойствами. Де Бройль предположил, что с пучком электронов следует связывать длину волны, определяемую уравнением
где $hbar$ – постоянная Планка ($6,626cdot 1034 Джcdot с$ или $6,626cdot 10-27 эргcdot с$), а $p$ – количество движения (импульс) электрона в пучке, т.е. его масса, умноженная на его скорость.
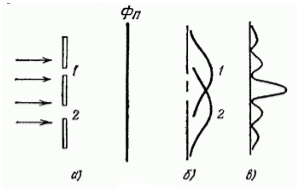
Физическое подтверждение волновой природы электрона было продемонстрировано в 1927 – 1928 гг. Дейвиссоном, Джермером и Томсоном, которые показали, что пучок электронов может испытывать дифракцию на подходящей решетке (атомы в кристалле золота), аналогичную дифракции пучка света.
Рисунок 1. Дифракция пучка электронов
На преграду с двумя узкими щелями направлен параллельный пучок моноэнергетических (т.е. обладающих одинаковой кинетической энергией) электронов (рис. 1. а). За преградой находится фотопластина $Фn$. При закрытии щели номер $2$ и экспонировании в течение времени $t$ почернение на проявленной фотопластине будет характеризоваться кривой $1$ (рис. 1. б). При закрытии щели номер $1$, соответственно, почернение на фотопластине будет соответствовать кривой $2$. Однако в случае, когда открыты обе щели картина почернения фотопластины (рис. 1. в) отнюдь не эквивалентна наложению двух первых картин. Зато она аналогична картине, получающейся при интерференции двух когерентных световых волн.
Готовые работы на аналогичную тему
Тот факт, что системы малых частиц проявляют, по крайней мере, при определенных условиях, волновые свойства, предполагает возможность описания таких систем уравнениями, подобными те, которые описывают другие виды волнового движения, например, волны, которые распространяются вдоль колеблющейся струны, или волновое движение, приписываемое электромагнитному излучению. Действительно, можно начать с волнового уравнения, соответствующего электромагнитным волнам, и путем определенных замен, превратить его в уравнение, соответствующее нашему случаю. Хотя эти замены диктуются физическими причинами, они в основном произвольны и могут быть приняты только потому, что приводят к уравнению, которое, как показывает опыт, позволяет получить правильное решение физических задач. Поэтому следует принять волновое уравнение как постулат, так как у химиков основной интерес вызывает применение волнового уравнения к атомным и молекулярным системам, а не физические и математические соображения, которыми руководствовался Шредингер, впервые его предложивший в 1925 г.
Видео:Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

Общий вид уравнения Шредингера
Рисунок 2. Эрвин Шрёдингер (1887 — 1961)
Волновое уравнение, применяемое для расчета стационарных состояний системы, можно записать в символическом виде:
где $H$ представляет собой определенный способ выражения общей энергии системы, а $E$ – числовое значение этой энергии. Для всех систем, которые обычно интересуют химиков, общая энергия представляет собой сумму кинетической энергии $Т$ и потенциальной энергии $V$:
Это соотношение было широко использовано физиком-теоретиком Гамильтоном, поэтому $H$ часто называют функцией Гамильтона, а $mathcal H$ гамильтонианом системы.
Видео:Квантовые числа (видео 14) | Квантовая физика | ФизикаСкачать

Уравнение Шредингера на примере атома водорода
Рассмотрим модель атома водорода, предложенную Бором. Для простоты предположим, что тяжелое ядро закреплено (оно почти, но не совершенно неподвижно, когда электрон движется вокруг него). Тогда полная кинетическая энергия $Т$ системы представляет собой просто кинетическую энергию электрона
где $m$ – масса электрона и $nu$ – его скорость. Потенциальная энергия системы есть просто энергия, возникающая вследствие электростатического взаимодействия (гравитационные силы приблизительно в $10^$ раз меньше), и ее можно выразить как
где $e$ — заряд электрона, $r$ — радиус орбиты, знак минус появляется вследствие того, что заряд одной из частиц положителен $(+)$, а другой отрицателен $(-)$. Поэтому для атома водорода функция Гамильтона в классической (т.е. доквантовомеханической) физике равна:
Если использовать понятие количества движения электрона $p=mnu$, данное уравнение запишется в следующем виде:
Теперь для перехода от классического описания этой или какой-либо другой системы к описанию при помощи волновой механики, необходимо взять функцию Гамильтона (уравнение 6) и произвести в ней определенные замены: в функции Гамильтона количество движения следует заменить выражением
Таким образом, гамильтониан для атома водорода в его квантовомеханической форме $$ следует записать в виде
Если теперь это выражение гамильтониана подставить в общее волновое уравнение (уравнение 1), то получим:
Это и есть волновое уравнение для атома водорода. Из уравнения 9 следует, что нужно вторые производные функции $psi $ сложить и умножить на $-<^2>/<8^2m>$, затем к этому добавить $left(-/right)psi $, тогда получим величину, тождественную Е$psi $. Если найдена функция $psi $, то говорят, что она является решением волнового уравнения, и ее называют волновой функцией. Вообще, может быть несколько различных функций $psi_1$, $psi_2$, . , $psi_n$, которые являются решениями уравнения 9, причем каждой соответствует свое значение энергии $Е_1$, $Е_2$, . , $Е_n$.
Видео:Энергетические уровни атома (видео 6) | Квантовая физика | ФизикаСкачать

Уравнение шредингера для стационарных состояний электрона находящегося в атоме водорода
Аналог классического волнового уравнения был предложен Э. Шредингером в 1925 г. Как и классическое уравнение, уравнение Шредингера связывает производные волновой функции по времени и координате. Уравнение Шредингера описывает поведение любых нерелятивистских систем. На примерах частицы, находящейся в бесконечно глубокой яме, и гармонического осциллятора рассмотрены простейшие квантовые системы, получены дискретные спектры состояний. Возможности описания динамики данных систем ограничены набором квантовых чисел, отражающих универсальные и внутренние симметрии квантовых систем.
4.1. Уравнение Шредингера
В квантовой физике изменение состояния частицы описывается уравнением Шредингера
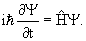 | (4.1) |
где 
в которой 







х → 


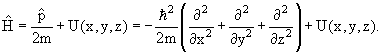 | (4.2) |
Уравнение Шредингера
Зависящее от времени уравнение Шредингера:
где 
Разделение переменных. Запишем Ψ(




Левая часть является функцией только координат, а правая не зависит от переменной x. Поэтому обе части последнего уравнения должны быть равны одной и той же постоянной, которую обозначим E
θ(t) = exp(−iEt/ћ), 




Уравнение 


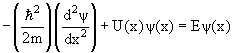
Для трехмерной системы с массой m в поле с потенциалом U(
−(ћ 2 /2m)Δψ(



где Δ – лапласиан.
Так как уравнение Шредингера является линейным уравнением первого порядка по времени, то с его помощью по заданному значению волновой функции Ψ(x, y, z, 0) в момент времени t = 0 можно найти её значение в произвольный момент времени t − Ψ(x, y, z, t).
Уравнение Шредингера для стационарного состояния, когда потенциальная энергия частицы не зависит от времени, имеет вид
 ψ( ψ( ) = Eψ( ) = Eψ( ). ). | (4.3) |
Это уравнение называют стационарным уравнением Шредингера.
Так как в стационарном состоянии
Ψ( ,t) = ψ( ,t) = ψ( )exp(−iEt/ћ) )exp(−iEt/ћ) | (4.4) |
и вероятность найти частицу в момент t в точке x, y, z пропорциональна |Ψ(
|ψ(x,y,z)| 2 , т.е. не зависит от времени. Аналогично, вероятность обнаружить значение физической величины, характеризующей систему, также не изменяется со временем, поскольку выражается через квадрат модуля волновой функции.
4.2. Частица в одномерной прямоугольной яме с бесконечными стенками
Потенциальная энергия U(x) в прямоугольной яме удовлетворяет следующим условиям:
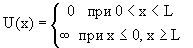 | (4.5) |
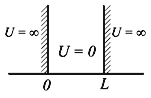
Рис.4.1. Прямоугольная яма с бесконечными стенками
Частица находится в области 0 ≤ x ≤ L. Вне этой области ψ(x) = 0. Уравнение Шредингера для частицы, находящейся в области 0 ≤ x ≤ L
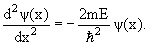 | (4.6) |
Волновая функция, являющаяся решением уравнения (4.9), имеет вид
| ψ(x)= Аsin kx + Bcos kx, | (4.7) |
где k = (2mE/ћ 2 ) 1/2 . Из граничных условий ψ(0) = 0, ψ(L) = 0 и условий непрерывности волновой функции следует
| Аsin kL = 0. | (4.8) |
kL = nπ, n = 1, 2, 3, … , то есть внутри потенциальной ямы с бесконечно высокими стенками устанавливаются стоячие волны, а энергия состояния частиц имеет дискретный спектр значений En
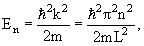 n = 1, 2, 3, … n = 1, 2, 3, … | (4.9) |
Частица может находиться в каком-то одном из множества дискретных состояний, доступных для неё.
Каждому значению энергии En соответствует волновая функция ψn(x), которая с учетом условия нормировки
 | (4.10) |
В отличие от классической, квантовая частица в прямоугольной яме не может иметь энергию
E 2 π 2 /(2mL 2 ). Состояния частицы ψn в одномерном поле бесконечной потенциальной ямы полностью описывается с помощью одного квантового числа n. Спектр энергий дискретный.
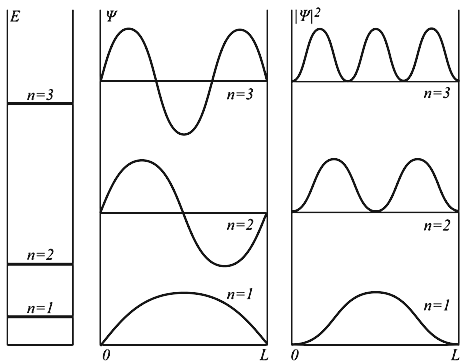
Рис. 4.2. Уровни энергии и волновые функции частицы Ψ в бесконечной прямоугольной яме. Квадрат модуля волновой функции |Ψ| 2 определяет вероятность нахождения частицы в различных точках потенциальной ямы.
4.3. Гармонический осциллятор
Положение уровней частицы в потенциальной яме зависит от вида потенциальной ямы. В одномерной потенциальной яме гармонического осциллятора потенциальная энергия имеет вид
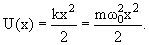 | (4.11) |
В этом случае одномерное уравнение Шредингера имеет вид
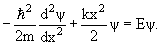 | (4.12) |
Допустимые значения полной энергии определяются формулой
| En = ћω0(n + 1/2), n = 0, 1, 2, | (4.13) |
В отличие от бесконечной прямоугольной ямы, спектр уровней гармонического осциллятора эквидистантный.
С увеличением массы частицы или размеров области ее локализации квантовое описание частицы переходит в классическое.
Частица в одномерной потенциальной яме
Одномерная прямоугольная яма шириной L:
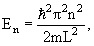

Одномерный гармонический осциллятор:
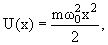
4.4. Частица в поле с центральной симметрией
В сферических координатах стационарное уравнение Шредингера для частицы в центральном потенциале U(r) имеет вид
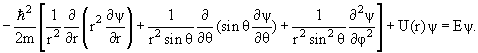 | (4.14) |
Решение уравнения (4.14) записываются в виде произведения радиальной и угловой функций
| ψ(r,θ,φ) = Rnl(r)Ylm(θ,φ), | (4.15) |
где радиальная функция Rnl(r) и угловая функция Ylm(θ,φ), называемая сферической, удовлетворяют уравнениям
 2 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) 2 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) | (4.16) |
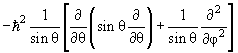 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) 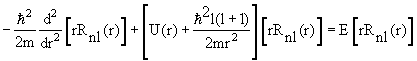 | (4.17) |
Уравнение (4.16) определяет возможные собственные значения l и собственные функции Ylm(θ,φ) оператора квадрата момента 
Схема уровней (последовательность и абсолютные значения энергий) зависит от радиальной функции Rnl(r), которая в свою очередь определяется потенциалом U(r), в котором находится частица.
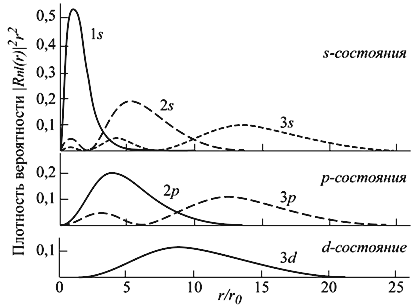
Рис. 4.3. Радиальное распределение вероятности нахождения электрона в кулоновском поле протона (атом водорода). Расстояния даны в боровских радиусах
r0 = ћ 2 /mee 2 ≈ 0.529·10 8 cм.
| Решения уравнения |
существуют лишь при определенных значениях квантовых чисел n (радиальное квантовое число), l (орбитальное квантовое число) и m (магнитное квантовое число).
Возможные энергетические состояния системы (уровни энергии) определяются числами n и l и в случае сферически симметричных состояний не зависят от квантового числа m. Число n может быть только целым:
n = 1, 2, …, ∞. Число l может принимать значения 0, 1, 2, …, ∞.
4.5. Орбитальный момент количества движения
Собственные значения L 2 и Lz являются решением уравнений


Они имеют следующие дискретные значения
L 2 = ћ 2 l(l + 1), где l = 0, 1, 2, 3, …,
Lz = ћm, где m = 0, ± 1, ± 2, ± 3,…, ± l.
Для характеристики состояний с различными значениями орбитального момента l обычно используют следующие обозначения:
Спектроскопические названия орбитальных моментов l
| l = 0 | s-состояние |
| l = 1 | p-состояние |
| l = 2 | d-состояние |
| l = 3 | f-состояние |
| l = 4 | g-состояние |
| l = 5 | h-состояние |
| и. т. д. |
Состоянию с l = 0 отвечает сферически симметричная волновая функция. В тех случаях, когда l ≠ 0 волновая функция не имеет сферической симметрии. Симметрия волновой функции определяется симметрией сферических функций Ylm(θ,φ). Имеет место интересное квантовое явление, когда решение сферически симметричной задачи (потенциал описывает сферически симметричную систему) приводит к состояниям, не обладающим сферической симметрией. Таким образом, симметрия уравнений не обязательно должна отражаться в симметрии каждого отдельно взятого решения этих уравнений, а лишь во всей совокупности этих решений.
Для частицы, находящейся в сферически симметричном потенциале, величина орбитального момента количества движения L:
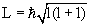 | (4.18) |
Обычно, для упрощения, когда говорят о величине орбитального момента количества движения, называют этой величиной квантовое число l, имея в виду, что между l и L имеется однозначная связь (4.18).
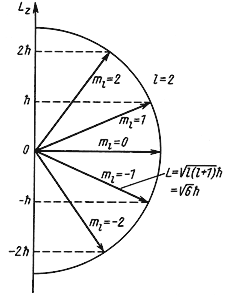
Рис. 4.4 Возможные ориентации вектора 
Так как величина l может принимать только целочисленные значения 0, 1, 2, 3,…, то и орбитальный момент количества движения L квантуется. Например, для частицы с l = 2 момент количества движения
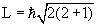
= 6.58·10 -22 √6 МэВ·сек ≈ 2.6·10 — 34 Дж·сек.
Пространственное квантование. Орбитальный момент количества движения является векторной величиной. Так как величина орбитального момента количества движения квантуется, то и направление 

Состояние частицы, находящейся в сферически симметричном поле, полностью описывается тремя квантовыми числами: n, l и m.
Появление квантовых чисел связано со свойствами симметрии системы. Характер этой симметрии определяет возможные значения квантовых чисел. Очевидно, что система, описываемая функцией e im φ , примет прежнее значение только тогда, когда азимутальный угол φ в результате поворота вокруг оси z примет прежнее значение φ. Этому условию функция e im φ удовлетворяет только в случае, когда величина mφ кратна 2π. Т.е. величина m должна иметь целые значения. Так как необходимо учитывать вращение в двух противоположных направлениях и отсутствие вращения, единственно возможными значениями оказываются m = 0, ±1, ±2, … .
4.6. Спин
Спин − собственный момент количества движения частицы. Между значением вектора спина 

 2 = ћ 2 s(s + 1) 2 = ћ 2 s(s + 1) | (4.19) |
В отличие от орбитального квантового числа l, которое может быть лишь целым числом или нулем, спиновое квантовое число s (в дальнейшем просто спин) может быть как целым (включая нуль), так и полуцелым, т. е. s = 0, 1/2, 1, 3/2, 2, 5/2, … , но при этом для каждой элементарной частицы спин может принимать единственное присущее этому типу частиц значение. Так, спины π-мезонов и К-мезонов равны 0. Спины электрона, протона, нейтрино, кварков и их античастиц равны 1/2. Спин фотона равен 1. Бозоны составляют класс частиц с целым значением спина, спин фермионов имеет полуцелое значение. Спин частицы невозможно изменить, также как её заряд или массу. Это её неизменная квантовая характеристика.
Как и в случае других квантовых векторов, проекция вектора спина 
szћ = ±sћ, ±(s − 1)ћ, ±(s − 2)ћ. ±1/2ћ или 0.
Число sz − это квантовое число проекции спина. Максимальная величина sz совпадает с s. Так как спин электрона равен 1/2, то проекция этого спина может принимать лишь два значения sz = ±1/2. Если проекция +1/2, то говорят, что спин направлен вверх, если проекция -1/2, то говорят, что спин направлен вниз.
4.7. Полный момент количества движения
Полный момент количества движения частицы или системы частиц 





Квадрат полного момента имеет значение:

Квантовое число полного момента j, соответствующее сумме двух векторов 

j = l + s, l + s −1. |l − s|
Проекция 
Число значений проекции Jz равно 2j + 1. Если для 

4.8. Квантовые числа
Квантовые числа – это целые или дробные числа, которые определяют все возможные значения физической величины, характеризующей различные квантовые системы – атомы, атомные ядра, кварки и другие частицы.
Таблица квантовых чисел
| n | Радиальное квантовое число. Определяет число узлов волновой функции и энергию системы. n = 1, 2, …, ∞. |
| J, j | Полный угловой момент J и его квантовое число j. Последнее никогда не бывает отрицательным и может быть целым или полуцелым в зависимости от свойств рассматриваемой системы.  2 = ћ 2 j(j + 1). 2 = ћ 2 j(j + 1). |
| L, l | Орбитальный угловой момент L и его квантовое число l. Интерпретация l такая же, как j, но l может принимать только целые значения, включая нуль: l = 0, 1, 2,…. L 2 = ћ 2 l(l + 1). |
| m | Магнитное квантовое число. Проекция полного или орбитального углового момента на выделенную ось (обычно ось z) равна mћ. Для полного момента m = ±j, ±(j-1), …, ±1/2 или 0. Для орбитального m = ± l, ± (l-1), …, ±1, 0. |
| S, s | Спиновый угловой момент S и его квантовое число s. Оно может быть либо положительным целым (включая нуль), либо полуцелым. s – неизменная характеристика частицы определенного типа. S 2 = ћ 2 s(s + 1). |
| sz | Квантовое число проекции спинового момента частицы на выделенную ось. Эта проекция может принимать значения szћ, где sz = ± s, ± (s -1), …, ±1/2 или 0. |
| P или π | Пространственная четность. Характеризует поведение системы при пространственной инверсии  → — → —  (зеркальном отражении). Полная четность частицы Р = π(-1) l , где π – её внутренняя четность, а (-1) l – её орбитальная четность. Внутренние четности кварков положительные, антикварков — отрицательные. (зеркальном отражении). Полная четность частицы Р = π(-1) l , где π – её внутренняя четность, а (-1) l – её орбитальная четность. Внутренние четности кварков положительные, антикварков — отрицательные. |
| I | Изоспин. Характеризует свойство зарядовой инвариантности сильных взаимодействий |
Для обозначения спинового момента часто используют букву J.
Все состояния, в которых может находиться квантовая система, описываются с помощью полного набора квантовых чисел. Так в случае протона в ядре состояние протона описывается с помощью четырех квантовых чисел, соответствующих четырем степеням свободы – трем пространственным координатам и спину. Это
- Радиальное квантовое число n ( 1, 2, …, ∞),
- Орбитальное квантовое число l (0, 1, 2, …),
- Проекция орбитального момента m (± l, ± (l-1), …, ±1, 0),
- Спин протона s =1/2.
Для описания сферически-симметричных систем в квантовой физике используются различные сферически симметричные потенциалы с различной радиальной зависимостью:
- Кулоновский потенциал U = Q/r,
- Прямоугольная потенциальная яма
- Потенциал типа гармонического осциллятора U = kr 2 ,
- Потенциал Вудса-Саксона (с его помощью описываются внутриядерные взаимодействия):
где U0, а и R – положительные константы (R – радиус ядра). Во всех случаях сферически симметричные системы можно описать с помощью набора квантовых чисел n, l, j, jz, однако, в зависимости от радиального вида потенциала энергетический спектр состояний системы будет различным.
Существование сохраняющихся во времени физических величин тесно связано со свойствами симметрии гамильтониана системы. Например, в случае, если квантовая система обладает центральной симметрией U = U(r), то этой системе соответствует сохранение орбитального момента количества движения l и одной из его проекций m. При этом из-за сферической симметрии задачи энергия состояний не будет зависеть от величины m, т. е. состояния будут вырожденными по m.
Наряду с пространственными симметриями, связанными с непрерывными преобразованиями, в квантовой физике существуют и другие симметрии – дискретные. Одной из них является зеркальная симметрия волновой функции относительно инверсии координат (

Система тождественных частиц характеризуется еще одной симметрией – симметрией относительно перестановок тождественных частиц. Эта симметрия определяется свойствами частиц, образующих систему. Системы частиц с целым спином (бозонов) описываются симметричными волновыми функциями, системы частиц с полуцелым спином (фермионов) − антисимметричными волновыми функциями.
Задачи
4.1. Вычислите допустимые уровни энергии электрона, находящегося в одномерной прямоугольной потенциальной яме шириной 10 -8 см, протона, находящегося в потенциальной яме 5 Фм, и шарика массой 1 г, находящегося в потенциальной яме 1 см.
4.2. Рассчитать энергию перехода между состояниями 1s и 2s в атоме водорода.
4.3. Найти значение полного момента j для протона в d-состоянии. Каким будет результат измерения полного момента протона в состоянии 1d5/2?
4.4. Найти полный момент (квантовое число j) системы двух нуклонов в s‑состоянии (l = 0).
4.5. Какие значения может иметь полный момент системы j, если
А. Нейтрон и протон находятся в состояниях с |l,s:j>n = |1, 1 /2: 3 /2>, |l,s:j>p = |1, 1 /2: 3 /2>?
Б. Два нейтрона находятся в состояниях с |l,s:j>1 = |1, 1 /2: 3 /2> и |l,s:j>2 = |1, 1 /2: 3 /2>?
4.6. А) Нейтрон находится в p-состоянии. Найти значения полного момента j и возможные значения проекции момента jz. Каким будет результат измерения орбитального момента частицы в этом состоянии? Б) Рассмотрите задачу А) для протона в d-состоянии.
Ответ: А) j = 3/2, 1/2; jz = ±3/2, ±1/2; L = ћ√ l(l +1) = √ 2 ћ;
Б) j = 5/2, 3/2; jz = ±5/2, ±3/2, ±1/2; L = ћ√ l(l +1) = √ 6 ћ
4.7. А) Частица с собственным моментом s = 3/2 находится в состоянии с орбитальным моментом
l = 2. Найти полный момент частицы j.
Б) Частица с собственным моментом s = 1/2 находится в состоянии с орбитальным моментом
l = 3. Определите полный момент частицы j
Ответ: А) j = 7/2 ÷ 1/2; Б) j = 7/2, 5/2
4.8. Протон и нейтрон находятся в состоянии с относительным орбитальным моментом L = 1. Найти полный момент системы J.
Ответ: J = 0, 1, 2
4.9. На оболочке с квантовым числом n = 1, l = 2 находятся протон и нейтрон. Определить их суммарный полный момент J и его проекцию Jz. Изменится ли результат, если на оболочке n = 1,
l = 2 будут находиться два нейтрона?
4.10. Почему возникают вырожденные состояния?
4.11. Написать оператор Гамильтона 
4.12. Напишите стационарное уравнение Шредингера в сферической системе координат.
4.13. Какие квантовые числа характеризуют частицу в центрально-симметричной потенциальной яме?
4.14. Покажите, что волновые функции ψ = Aexp(kx −ωt) и ψ = Asin(kx −ωt) не удовлетворяют зависящему от времени уравнению Шредингера.
4.15. Покажите, что волновые функции ψ = Ae i(kx −ωt) и ψ = A(cos(kx −ωt) − sin(kx −ωt))удовлетворяют зависящему от времени уравнению Шредингера.
4.16. Частица находится в низшем состоянии n = 1 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L.
А) Рассчитайте вероятность обнаружить частицу в интервале Δx = 0.001L при x = 1 /2L, x = 2 /3L, x = L.
Б) Рассмотрите случай, когда частица находится в состоянии n = 2 при тех же значениях x.
Ответ: А) P(L/2) = 0.002; P(2L/3) = 0.0015; P(L) = 0; Б) P(L/2) = 0; P(2L/3) = 0.0015; P(L) = 0
4.17. Частица находится в состоянии n = 2 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L. Рассчитайте вероятность обнаружить частицу в интервале ( 1 /3L, 2 /3L).
Ответ: P(L/3, 2L/3) = 0.2
4.18. Электрон находится всостонии n = 5 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L. Рассчитайте вероятность обнаружить электрон в области x от 0.2L до 0.5L.
Ответ: P(0.2L, 0.5L) = 0.3
4.19. Электрон находится в бесконечно глубокой одномерной потенциальной яме. Рассчитайте ширину потенциальной ямы, если энергия состояния n = 1 равна 0.1 эВ.
Ответ: L = 1.9 нм
4.20. Рассчитайте средние значения и 2 > для состояний n = 1, 2, 3 в бесконечно глубокой прямоугольной потенциальной яме.
4.21. Что общего и в чем различие в описании атома водорода в теории Шредингера и в модели Бора?
4.22. Почему энергии атома водорода в теории Шредингера не зависят от орбитального квантового числа l?
4.23. Угловой момент характеризуется квантовым числом l = 3. Какие значения могут принимать Lz и L 2 ?
Ответ: Lz = -3ћ, -2ћ. 3ћ; L 2 = 12ћ 2
4.24. Угловой момент характеризуется квантовым числом l = 3. Какие значения могут принимать Lz и L 2 ?
🎬 Видео
Спектр излучения водорода (видео 12) | Квантовая физика | ФизикаСкачать
Урок 459. Обзор квантовой теории атома водородаСкачать

Консультация по квантовой механике. Часть 6. "Энергетический спектр водородоподобных атомов"Скачать

ЧК МИФ 6 2 4 1(L4) _ Уравнение Шредингера для электрона в состояниях, зависящих от угловСкачать

Урок 454. Понятие о волновой функцииСкачать

Структура материи 6: уравнение Шрёдингера. Зачем нужна квантовая механика – Виталий Бейлин | НаучпопСкачать

Квантовые постулаты Бора. Модель атома | Физика 11 класс #43 | ИнфоурокСкачать

94. Теория Бора водородоподобных атомовСкачать

Классические уравнения | одномерное стационарное уравнение Шрёдингера | беск. потенц. яма | 1Скачать

ПОСТУЛАТЫ БОРА. Атомная физика. Подготовка к ЕГЭ по физике. ТехноскулСкачать

ЧК МИФ 6 2 1 2 Сферически симметричные состояния электрона в атома водородаСкачать

Квантовая механика 47 - Стационарное уравнение Шредингера. Гармонический осциллятор.Скачать

Уравнение Шредингера Стационарные состоянияСкачать

Воронина Е. Н. - Атомная физика. Семинары - Движение в центрально-симметричном полеСкачать

Рубцов А. Н. - Введение в квантовую физику - Волновая функция и уравнение ШредингераСкачать