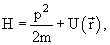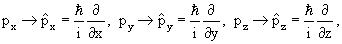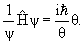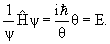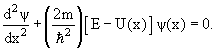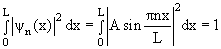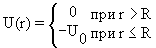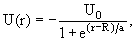- Конспект лекции с демонстрациями
- Уравнение шредингера для потенциальной ямы конечной глубины
- Примеры туннельного эффекта
- Аналогии из классической механики
- 10.2. Потенциальная яма конечной глубины
- Особенности решений для ямы конечной глубины
- 10.3. Рассеяние на потенциальном пороге
- 10.4. Рассеяние на потенциальной яме
- Уравнение шредингера для потенциальной ямы конечной глубины
- 4.1. Уравнение Шредингера
- Уравнение Шредингера
- 4.2. Частица в одномерной прямоугольной яме с бесконечными стенками
- 4.3. Гармонический осциллятор
- Частица в одномерной потенциальной яме
- 4.4. Частица в поле с центральной симметрией
- 4.5. Орбитальный момент количества движения
- 4.6. Спин
- 4.7. Полный момент количества движения
- 4.8. Квантовые числа
- Таблица квантовых чисел
- Задачи
- 🔍 Видео
Конспект лекции с демонстрациями
Аннотация: изучение качественной стороны решений уравнения Шредингера, выяснение отличий получаемых результатов от выводов классической механики. Традиционное изложение темы, дополненное двумя демонстрациями на компьютерных моделях.
Одна из простейших задач о движении микрочастиц это задача о движении в прямоугольной потенциальной яме с очень высокими стенками. Рассмотрим одномерный случай. (Трехмерные задачи сложны в математическом отношении, а практически все принципиальные особенности движения микрочастиц можно выявить и на одномерных задачах.) Изменение потенциальной энергии по оси x описывается формулой
Какие примеры движения окружающего мира хотя бы приближенно описываются такой потенциальной функцией?
- Вспомним «Кавказского пленника» (Л.Н.Толстой). Попавшего в плен Жилина держали в яме и требовали выкупа. Можно сказать, что для человека яма глубиной три метра это яма с бесконечно высокими стенками. В ней человек может находиться в любом из состояний от состояния покоя до интенсивного движения в бессильной ярости от невозможности выбраться на поверхность.
- Другой пример лототрон. В нем шарики либо лежат на дне, либо скачут в ограниченном стенками пространстве.
В мире микрочастиц взаимодействие протона и нейтрона в ядре тяжелого водорода приближенно описывается прямоугольным потенциалом. Этот же потенциал чрезвычайно грубое приближение к задаче о движении электрона в атоме. Существенным для всех примеров является ограничение движения некоторой областью значений x. Стенки «ящика» бесконечно круты и бесконечно высоки. Частица не может покинуть такую яму.
Всю область изменения переменной x разобьем на три (см. рисунок 1). Вероятность нахождения частицы в областях x a равна нулю, так что волновая функция Ψ(x) = 0. В центральной части мы положили для удобства U(x) = 0 (известно, что потенциальная энергия определена с точностью до константы). В этом случае уравнение Шредингера принимает вид

где m и E масса и полная энергия частицы, соответственно. Введем обозначение

Уравнение приобретает вид и имеет решение

Постоянные A, α и β мы найдем из условий непрерывности волновой функции и нормировки. На левой границе Ψ(0) = Asin(α) = 0 дает α = 0. На правой границе Ψ(a) = Asin(βa) = 0 приводит к βa = πn, где n = 1, 2, 3, . Нулевое значение n в ряд допустимых значений не входит, т.к. иначе волновая функция везде бы обращалась в ноль. Движение частицы в потенциальной яме описывается набором волновых функций


Окончательный вид волновой функции

Возведем в квадрат левую и правую части равенства βa = πn, и вспомним, что значит β 2 . Тогда получим выражение для энергии

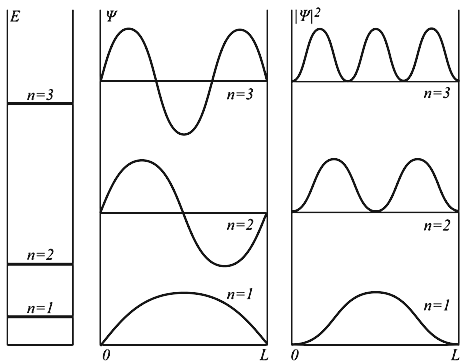
Самым важным результатом является то, что возможны только такие состояния, для которых E принимает одно из дискретных значений. Введенное выше число n называют квантовым числом. Значения En называют уровнями энергии. Говорят, что частица находится в квантовом состоянии n, если ее движение описывается волновой функцией Ψn(x). Три первых уровня энергии, соответствующие им волновые функции Ψ(x) и квадраты волновых функций изображены на рисунке 2.
Состояние с минимальной энергией (n = 1) называют основным, остальные — возбужденными. Обратите внимание на то, что энергия основного состояния не равна нулю. Про микрочастицы можно сказать «покой им только снится». Это общий результат квантовой механики, справедливый для всех ее задач и полностью чуждый классической механике.
Распределение плотности вероятности по координате |Ψ(x)| 2 неоднородно и зависит от n. Чем больше n, тем сильнее неоднородность. С классической точки зрения на частицу в яме не действуют никакие силы, и она с равной вероятностью может находиться в любой точке.
Расстояние между соседними уровнями энергии

Чем меньше масса частицы и ширина области движения, больше ΔE. Для электрона (масса порядка 10 -30 кг) в атоме (размер порядка 10 -10 м) получим ΔE
10 эВ, а для молекулы (масса
10 -27 кг) в сосуде (размер порядка 10 -1 м) ΔE
10 -20 эВ. В последнем случае (ширина ямы макроскопических масштабов) энергию молекулы можно считать непрерывно изменяющейся величиной.
Найдем еще относительное расстояние между уровнями

При больших значениях квантового числа (большие возбуждения) дискретность состояний перестает проявляться. Фактически наблюдаем переход к непрерывному изменению энергии.
Посмотрим на иллюстрации движения частиц. Они выполнены в виде апплета, который будет работать в отдельном окне. Положение подвижной стрелки задает энергию частицы Е. Плавно передвиньте ее в верхнее положение. Если текущее значение Е разрешено законами физики, то строится график зависимости плотности вероятности P нахождения частицы от ее координаты. Слева графики строятся по формулам, полученным выше в результате решения уравнения Шредингера. Справа предсказания классической физики. Одновременно наблюдайте за иллюстрацией одномерного движения частицы в нижней части окна. (Беру, как говорится, «грех на душу», изображая движение микрочастиц. Для них не применимо понятие траектории. Но об этом в следующих лекциях.) Если щелкнуть мышкой по ссылке, откроется демонстрация (После щелчка по кнопке «Старт» Вы только наблюдаете).
После прочитанного и увиденного рассортируйте 6 утверждений, приведенных ниже, по двум столбцам. Для этого щелкайте по нужной стрелке.
| Квантовая физика | Классическая физика |
|---|
Движение частиц в потенциальной яме конечной глубины
Посмотрим, что изменится, если потенциальная яма будет иметь конечную глубину



Во втором слагаемом коэффициент перед Ψ отрицателен. Обозначим его

Уравнения Шредингера вне и внутри ямы отличаются знаком перед Ψ
и имеют решения

Надо сразу положить A1 = B3 =0, чтобы решения не увеличивались беспредельно в области больших отрицательных и больших положительных значениях x. Для нахождения остальных коэффициентов надо использовать условия непрерывности волновой функции Ψ и ее первой производной dΨ/dx в точках x = 0 и x = a. Здесь мы ограничимся обсуждением качественно новых результатов. Решения вне ямы апериодические, быстро спадающие. Например, в области 3

Отличие от нуля волновой функции Ψ(x) (а, следовательно, и |Ψ| 2 )в первой и третьей областях это новый результат, которого нельзя было ожидать на основе классической теории. Напомним, что на рисунке 4 в области x > a энергия E -34 Дж·с, ожидать заметного эффекта для тел с макроскопической массой m или энергией U0 — E не приходится (при этом l → 0).
Возможные значения энергии, как и для ямы бесконечной глубины, квантованы. И полученная нами формула (1) остается хорошей аппроксимацией, особенно для больших U0 — E. Для получения точного значения необходимо решить численно трансцендентное уравнение. Отметим только, что число уровней в яме зависит от ее ширины и глубины. И может статься, в яме не окажется ни одного уровня. Это означает, что связанного состояния при данных параметрах не существует. Для дейтрона (U0
10 -15 м) существует только одно связанное состояние с энергией -2.2 МэВ.
Компьютерная модель проиллюстрирует характер движения микрочастицы (электрона) в потенциальной яме конечной глубины.
Возможности этой программы: после того, как Вы зададите ширину (в нм) и глубину (в эВ) ямы, компьютер проведет необходимые расчеты и будет готов показать разрешенные значения энергии и соответствующие им распределения плотности вероятности нахождения частицы по ширине ямы. При неудачной комбинации параметров (слишком высока плотность уровней, их отсутствие. ) компьютер выдаст предупреждение. После ввода параметров двигайте указатель вдоль оси энергий (мышкой или клавишами со стрелками) и наблюдайте.
Определите:
- как число уровней в яме зависит от ширины и глубины ямы;
- как энергия частицы зависит от квантового числа n (правый график);
- как вероятность обнаружить частицу в интервале 0 2 ;
- вероятность обнаружить частицу меняется от точки к точке;
- если значение квантового числа n устремить к бесконечности, решение переходит в классическое.
Если возникли какие-либо вопросы, напишите мне.
Видео:Воронина Е. Н. - Атомная физика. Семинары - Решение уравнения Шредингера для потенциальной ямыСкачать

Уравнение шредингера для потенциальной ямы конечной глубины
Выше мы познакомились с теми свойствами частиц, которые не наблюдаются в классической механике. К ним относятся: вырождение энергетических уровней в отсутствие внешних полей, дискретный спектр энергии в потенциальной яме и «просачивание» частицы в классически недоступную область потенциального порога.
В этой главе будет продолжено обсуждение чисто квантовых явлений, имеющих отношение к атомной физике. Мы познакомимся с туннельным эффектом — прохождением частицы сквозь потенциальный барьер конечной ширины. Далее убедимся, что в потенциальной яме не всегда есть дискретные уровни энергии, если глубина ямы ограничена. Наконец, в связи с эффектом Рамзауэра будут решены задачи о рассеянии на потенциальном барьере и потенциальной яме.
10.1. Потенциальный барьер
Потенциальный барьер, в отличие от рассмотренного в предыдущей главе потенциального порога, имеет конечную ширину. График зависимости U( x ) изображён синим цветом на рис. 10.1.1.
Потенциальная энергия равна своему пороговому значению U0 внутри промежутка [0, L], а снаружи обращается в нуль. Энергия налетающей частицы E отмечена зелёной линией, как и на рис. 9.4.1.
В предыдущей главе мы установили, что квантовую частицу можно обнаружить и в области, запрещённой для классического движения. Хотя вероятность обнаружения экспоненциально уменьшается по мере удаления от порога, тем не менее, в точке x = L она имеет некоторое отличное от нуля значение. Следовательно, частица может проникнуть сквозь потенциальный барьер. Такое явление называют «туннельным эффектом».
Здесь мы напишем основную формулу туннельного эффекта в её простейшем варианте, исходя из решения задачи о потенциальном пороге. А именно, будет рассмотрен случай сильного затухания проходящей волны на правой границе барьера:
Если это условие выполнено, то амплитуда отражённой волны невелика, и в первом приближении её можно не учитывать. Тогда ответ получается сразу. В области 
(обозначения соответствуют разделу 9.4 предыдущей главы). Подставляя сюда выражение для k2 из (9.4.7), получим окончательно
Условие (1.2) выполняется, если показатель экспоненты велик по абсолютной величине.
Формулу (1.3) можно обобщить на случай потенциального барьера произвольной формы. Если функция U( x ) меняется от точки к токе, как это показано на рис. 10.1.2, то
поступаем следующим образом. Интервал 
В силу независимости отдельных элементарных событий, вероятность прохождения через весь барьер равна произведению
В пределе разбиваем весь интервал на бесконечно малые промежутки dx и переходим от суммы к интегралу:
Перейдём к изложению физических явлений, в которых имеет место туннельный эффект.
Видео:97. Микрочастица в потенциальной ямеСкачать

Примеры туннельного эффекта
Самыми известными проявлениями туннельного эффекта являются ядерные реакции и холодная эмиссия металлов.
Впервые задачу о слиянии двух ядер решил Гамов. Примером такой реакции является слияние двух ядер дейтерия в a –ч астицу:
d ( n , p ) + d ( n , p ) ® He (2p, 2n).
Реакция синтеза — экзотермическая. График потенциальной энергии взаимодействия ядер схематически приведён на рис. 10.1.3 синим цветом.
Внутри ядра радиуса 
В точке 
Примером процесса, обратного синтезу ядер, может служить a –р аспад:
Здесь А — массовое число химического элемента (суммарное число протонов и нейтронов в ядре), а Z — число протонов. Реакция (1.4) заключается в проникновении a –ч астицы сквозь потенциальный барьер из ядра в область действия кулоновских сил.
3 Холодная эмиссия металлов.
Энергетические уровни электронов в металле ограничены сверху так называемой энергией Ферми EF. Электроны не покидают металл, так как находятся перед потенциальным барьером U0, обладающим практически бесконечной протяжённостью. Этот барьер на правом чертеже рис.10.1.4 нарисован синей линией. Зелёным цветом помечена энергия Ферми, а чёрные линии изображают уровни энергии.
В электрическом поле с напряжённостью E потенциальная энергия U( x ) линейно зависит от координаты x , отсчитываемой от поверхности проводника:
На правом рисунке зависимость U( x ) обозначена синим цветом. Эффективная толщина барьера становится конечной, и, как следствие, с поверхности металла начинает выходить поток электронов.
Видео:Урок 456. Движение микрообъекта в одномерной бесконечно глубокой потенциальной ямеСкачать

Аналогии из классической механики
Товарный поезд на рис.10.1.5 преодолевает сортировочную горку. Точечный объект был бы
вынужден развить большую скорость, так как он весь сразу должен пересечь вершину. Но локомотив въезжает сначала сам, потом первый вагон, затем — второй и так далее. Таким образом, поезд «перетекает» через горку по частям, как гусеница. Решение нестационарного уравнения Шредингера показывает, что эта аналогия частично соответствует картине преодоления барьера волновым пакетом, представляющим частицу. Первоначальный пакет разбивается на более мелкие, часть из них проходит через потенциальный барьер, а остальные — отражаются.
Видео:1-D finite Square Well/Электрон в одномерной потенциальной яме конечной глубиныСкачать

10.2. Потенциальная яма конечной глубины
Потенциальная яма прямоугольной формы схематически изображена на рис.10.2.1.
Зависимость U( x ) выражается функцией
Метод решения аналогичен применённому в предыдущих задачах, однако расчёты в данном случае более громоздки. Отличие волновой функции и энергетических уровней от тех, которые получаются в задаче о бесконечно глубокой потенциальной яме, мы получим с помощью качественных рассуждений. Для этого мы сначала уточним некоторые свойства одномерного уравнения Шредингера. Переписав его в форме
убеждаемся, что знак y ( x ) совпадает со знаком 
Все они могут быть описаны экспонентой
с действительным параметром k , положительным или отрицательным. Как видно на рис.10.2.2, первый и четвёртый варианты не годятся для физических приложений, так как они описывают
функции с бесконечно возрастающим модулем при увеличении x .
Выясним поведение волновой функции при E > U. На рис.10.2.3 приведены все варианты кривых с отрицательной кривизной.
Они же перечислены в следующей таблице:
Теперь для описания всех кривых подходит функция
Таким образом, при условии E > U реализуются осциллирующие решения, если же E U, то волновая функция экспоненциально затухает. Учёт граничных условий — непрерывность волновой функции вместе с её первой производной — всё это соответствует одновременной подгонке амплитуды b в экспоненциальной форме и фазы j в представлении гармонической функции.
Вернёмся к рассматриваемой задаче. Построим качественно решение для случая E U0. В центре, 0 x L, решение описывается гармонической функцией, а по краям оно экспоненциально затухает. График волновой функции схематически изображён на рис.10.2.4. Меняя фазу осцилляций и амплитуды экспонент, мы сшиваем
все три участка области изменения волновой функции. Все эти операции аналогичны тем, что были выполнены в предыдущей главе, когда мы решали задачу о частице, налетающей на потенциальный порог. Рис. 10.2.4 аналогичен рис. 9.4.2. Сшивка возможна лишь в том случае, если внутри ямы укладывается целое число полуволн. Таким образом, снова получаем квантование энергетических уровней.
Видео:Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

Особенности решений для ямы конечной глубины
Яма конечной глубины объединяет в себе свойства бесконечно глубокой ямы и потенциального барьера. Внутри ямы имеет место осциллирующее решение, а при x x > L волновая функция «просачивается» наружу. Выше мы получили, что величина просачивания растёт с уменьшением модуля разности | U0 – E|. Просачивание вызывает растягивание узлов и, как следствие — снижение уровней энергии. Чем выше лежит уровень, тем дальше за пределы отрезка (0, L) уходит волновая функция. Это означает, что с увеличением квантового числа n в б óльшей мере возрастает расстояние между узлами, а вместе с ним — и длина волны. Напомним, что энергия обратно пропорциональна квадрату дебройлевской длины волны:
Следовательно, с ростом n уровни опускаются всё глубже по сравнению с их положением в яме с бесконечно высокими стенками. На рис. 10.2.5 изображены уровни энергии 

L. Минимально возможная энергия E min связанного состояния получается из соотношения неопределенностей, где точность локализации частицы полагаем равной ширине ямы L:
Связанные состояния существуют, если
то есть при выполнении неравенства
Положение уровня определяется произведением 
Видео:Урок 455. Уравнение ШрёдингераСкачать

10.3. Рассеяние на потенциальном пороге
Задача ставится следующим образом. Частица, двигаясь слева направо с энергией E, налетает на потенциальный барьер U0 E, расположенный на рис. 10.3.1 в точке x = 0. График функции U( x), как и прежде, обозначим синим цветом, а энергию частицы — зелёным. В классической механике частица преодолевает порог, испытывая некоторое торможение на участке (0, L). Обсудим поведение квантовой частицы. Стрелками помечены
амплитуда падающей волны ( A), а также прошедшей ( B) и отражённой ( C) волн. Аналогичная задача уже была решена в четвёртом разделе предыдущей главы, но для случая, когда энергия частицы меньше высоты порога. Там мы убедились, что существует вероятность проникновения частицы внутрь порога. Здесь же мы увидим, что частица может испытать отражение, несмотря на то, что её энергия превышает высоту барьера.
Приступим к решению задачи. По аналогии с разделом 9.4 введём следующие обозначения:
для области слева от барьера и
справа от барьера. Очевидно, 
Слева от барьера волновая функция равна сумме падающей и отражённой волн,
в то время как справа от разрыва распространяется только прошедшая волна:
были выведены в разделе 9.4 предыдущей главы. Напомним, что они отражают отсутствие процессов рождения и гибели частиц, а также ограниченность потенциала. С их помощью мы можем выразить два неизвестных параметра в (3.2) через третий, например, так:

Коэффициент отражения R равен отношению квадратов амплитуд падающей и отражённой волн:
Отсюда видно, что вероятность отражения отлична от нуля при любом значении энергии налетающей частицы. В этом проявляются её квантовые свойства. Правда, при 
Аналогия с классической механикой наблюдается также при максимально возможном понижении энергии частицы. Если величина E практически не отличается от высоты порога: 
Рассмотрим теперь иной вариант задачи: частица «падает из-за порога». На рис.10.3.2
области слева и справа от разрыва поменялись местами по сравнению с рис.10.3.1. Поэтому можно воспользоваться решением предыдущей задачи, выполнив замену 
Коэффициент отражения предыдущем случае. Однако , имеется и существенное различие. Легко убедиться, что знаки C и A в (3.3) одинаковы, а в (3.5) — противоположны. Таким образом, падающая и отражённая волны находятся в противофазе.
В классической физике имеется аналог этого явления. В третьем разделе пятой главы приведена « оптико –механическая аналогия»: импульс частицы p или волновое число k являются аналогами показателя преломления n , причём n является растущей функцией k . Из оптики известно, что отражение от оптически более плотной среды (3.5) происходит без изменения фазы, а при отражении от менее плотной среды (3.3) фаза меняется на π . Итак, в первом случае (падение на порог) происходит потеря полуволны.
Сбой фазы имеет важные последствия для рассеяния на потенциальной яме. В самом деле, потенциальную яму можно составить из двух порогов. Если между двумя разрывами укладывается целое число полуволн, то две отражённые волны компенсируют друг друга, и отражённая волна пропадает. Так как дебройлевская длина волны связана с импульсом частицы, то «провал» отражения имеет место для частиц определённых энергий. Рассмотрим рассеяние на потенциальной яме подробнее.
Видео:Частица в одномерной потенциальной ямеСкачать

10.4. Рассеяние на потенциальной яме
Задача предыдущего раздела позволит нам понять интересные квантовые эффекты, имеющие место при рассеянии на потенциальной яме. На рис. 10.4.1 присутствуют амплитуды уже пяти волн:
B — прошедшей через первый барьер,
D — отражённой от первого барьера,
F — отражённой от второго барьера,
C — прошедшей через второй барьер.
Амплитуда F с точностью до потерь на отрезке (0, L) равна D по модулю и противоположна по знаку. Если на ширине ямы укладывается целое число полуволн, то в области 
Рассматриваемая задача имеет строгое решение. Бросаем на потенциальную яму волну с амплитудой A и записываем выражения для волновой функции на трёх участках:
Параметры k1 и k2 определены в (3.1). Граничные условия для волновой функции на двух границах
приводят к системе из четырёх линейных уравнений с пятью неизвестными. Все искомые амплитуды можно выразить через одну из них, например через A. Опуская простые, но длинные вычисления, приведём окончательное выражение для коэффициента отражения:
Из этого соотношения вытекает, что коэффициент отражения обращается в нуль не только в уже известном нам случае больших энергий налетающей частицы. Отражение отсутствует также, когда ширина ямы равна целому числу полуволн и волны, отражённые от двух краёв ямы, гасят друг друга:
Полученный результат объясняет так называемый эффект Рамзауэра, наблюдаемый при упругом рассеянии электронов на атомах благородных газов: аргона, криптона и ксенона. Он заключается в том, что вероятность рассеяния резко уменьшается при некоторых значениях энергии электрона, как это схематически показано на рис. 10.4.2.
Наличие «провала» можно объяснить следующим образом. Атом инертного газа представляет собой компактное образование ( заполненные подоболочки ). Так что потенциал взаимодействия в грубом приближении можно заменить потенциальной ямой с резко очерченными краями. При определённых значениях энергии электрона E m на отрезке длиной L может уложиться целое число полуволн. Две волны, отражённые от краёв ямы, гасятся, и электрон пролетает свободно, не испытывая взаимодействия.
Видео:Атомная физика. Лекция 13. Движение частицы в одномерной потенциальной яме конечной глубиныСкачать

Уравнение шредингера для потенциальной ямы конечной глубины
Аналог классического волнового уравнения был предложен Э. Шредингером в 1925 г. Как и классическое уравнение, уравнение Шредингера связывает производные волновой функции по времени и координате. Уравнение Шредингера описывает поведение любых нерелятивистских систем. На примерах частицы, находящейся в бесконечно глубокой яме, и гармонического осциллятора рассмотрены простейшие квантовые системы, получены дискретные спектры состояний. Возможности описания динамики данных систем ограничены набором квантовых чисел, отражающих универсальные и внутренние симметрии квантовых систем.
4.1. Уравнение Шредингера
В квантовой физике изменение состояния частицы описывается уравнением Шредингера
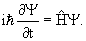 | (4.1) |
где 
в которой 







х → 


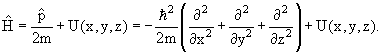 | (4.2) |
Уравнение Шредингера
Зависящее от времени уравнение Шредингера:
где 
Разделение переменных. Запишем Ψ(




Левая часть является функцией только координат, а правая не зависит от переменной x. Поэтому обе части последнего уравнения должны быть равны одной и той же постоянной, которую обозначим E
θ(t) = exp(−iEt/ћ), 




Уравнение 


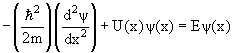
Для трехмерной системы с массой m в поле с потенциалом U(
−(ћ 2 /2m)Δψ(



где Δ – лапласиан.
Так как уравнение Шредингера является линейным уравнением первого порядка по времени, то с его помощью по заданному значению волновой функции Ψ(x, y, z, 0) в момент времени t = 0 можно найти её значение в произвольный момент времени t − Ψ(x, y, z, t).
Уравнение Шредингера для стационарного состояния, когда потенциальная энергия частицы не зависит от времени, имеет вид
 ψ( ψ( ) = Eψ( ) = Eψ( ). ). | (4.3) |
Это уравнение называют стационарным уравнением Шредингера.
Так как в стационарном состоянии
Ψ( ,t) = ψ( ,t) = ψ( )exp(−iEt/ћ) )exp(−iEt/ћ) | (4.4) |
и вероятность найти частицу в момент t в точке x, y, z пропорциональна |Ψ(
|ψ(x,y,z)| 2 , т.е. не зависит от времени. Аналогично, вероятность обнаружить значение физической величины, характеризующей систему, также не изменяется со временем, поскольку выражается через квадрат модуля волновой функции.
4.2. Частица в одномерной прямоугольной яме с бесконечными стенками
Потенциальная энергия U(x) в прямоугольной яме удовлетворяет следующим условиям:
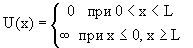 | (4.5) |
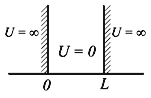
Рис.4.1. Прямоугольная яма с бесконечными стенками
Частица находится в области 0 ≤ x ≤ L. Вне этой области ψ(x) = 0. Уравнение Шредингера для частицы, находящейся в области 0 ≤ x ≤ L
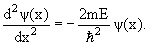 | (4.6) |
Волновая функция, являющаяся решением уравнения (4.9), имеет вид
| ψ(x)= Аsin kx + Bcos kx, | (4.7) |
где k = (2mE/ћ 2 ) 1/2 . Из граничных условий ψ(0) = 0, ψ(L) = 0 и условий непрерывности волновой функции следует
| Аsin kL = 0. | (4.8) |
kL = nπ, n = 1, 2, 3, … , то есть внутри потенциальной ямы с бесконечно высокими стенками устанавливаются стоячие волны, а энергия состояния частиц имеет дискретный спектр значений En
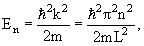 n = 1, 2, 3, … n = 1, 2, 3, … | (4.9) |
Частица может находиться в каком-то одном из множества дискретных состояний, доступных для неё.
Каждому значению энергии En соответствует волновая функция ψn(x), которая с учетом условия нормировки
 | (4.10) |
В отличие от классической, квантовая частица в прямоугольной яме не может иметь энергию
E 2 π 2 /(2mL 2 ). Состояния частицы ψn в одномерном поле бесконечной потенциальной ямы полностью описывается с помощью одного квантового числа n. Спектр энергий дискретный.
Рис. 4.2. Уровни энергии и волновые функции частицы Ψ в бесконечной прямоугольной яме. Квадрат модуля волновой функции |Ψ| 2 определяет вероятность нахождения частицы в различных точках потенциальной ямы.
4.3. Гармонический осциллятор
Положение уровней частицы в потенциальной яме зависит от вида потенциальной ямы. В одномерной потенциальной яме гармонического осциллятора потенциальная энергия имеет вид
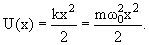 | (4.11) |
В этом случае одномерное уравнение Шредингера имеет вид
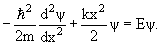 | (4.12) |
Допустимые значения полной энергии определяются формулой
| En = ћω0(n + 1/2), n = 0, 1, 2, | (4.13) |
В отличие от бесконечной прямоугольной ямы, спектр уровней гармонического осциллятора эквидистантный.
С увеличением массы частицы или размеров области ее локализации квантовое описание частицы переходит в классическое.
Частица в одномерной потенциальной яме
Одномерная прямоугольная яма шириной L:
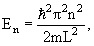

Одномерный гармонический осциллятор:
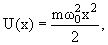
4.4. Частица в поле с центральной симметрией
В сферических координатах стационарное уравнение Шредингера для частицы в центральном потенциале U(r) имеет вид
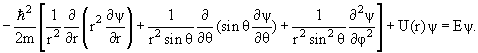 | (4.14) |
Решение уравнения (4.14) записываются в виде произведения радиальной и угловой функций
| ψ(r,θ,φ) = Rnl(r)Ylm(θ,φ), | (4.15) |
где радиальная функция Rnl(r) и угловая функция Ylm(θ,φ), называемая сферической, удовлетворяют уравнениям
 2 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) 2 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) | (4.16) |
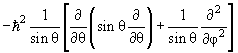 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) 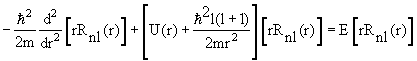 | (4.17) |
Уравнение (4.16) определяет возможные собственные значения l и собственные функции Ylm(θ,φ) оператора квадрата момента 
Схема уровней (последовательность и абсолютные значения энергий) зависит от радиальной функции Rnl(r), которая в свою очередь определяется потенциалом U(r), в котором находится частица.
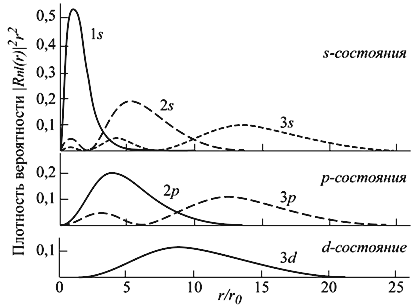
Рис. 4.3. Радиальное распределение вероятности нахождения электрона в кулоновском поле протона (атом водорода). Расстояния даны в боровских радиусах
r0 = ћ 2 /mee 2 ≈ 0.529·10 8 cм.
| Решения уравнения |
существуют лишь при определенных значениях квантовых чисел n (радиальное квантовое число), l (орбитальное квантовое число) и m (магнитное квантовое число).
Возможные энергетические состояния системы (уровни энергии) определяются числами n и l и в случае сферически симметричных состояний не зависят от квантового числа m. Число n может быть только целым:
n = 1, 2, …, ∞. Число l может принимать значения 0, 1, 2, …, ∞.
4.5. Орбитальный момент количества движения
Собственные значения L 2 и Lz являются решением уравнений


Они имеют следующие дискретные значения
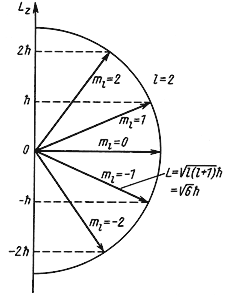
L 2 = ћ 2 l(l + 1), где l = 0, 1, 2, 3, …,
Lz = ћm, где m = 0, ± 1, ± 2, ± 3,…, ± l.
Для характеристики состояний с различными значениями орбитального момента l обычно используют следующие обозначения:
Спектроскопические названия орбитальных моментов l
| l = 0 | s-состояние |
| l = 1 | p-состояние |
| l = 2 | d-состояние |
| l = 3 | f-состояние |
| l = 4 | g-состояние |
| l = 5 | h-состояние |
| и. т. д. |
Состоянию с l = 0 отвечает сферически симметричная волновая функция. В тех случаях, когда l ≠ 0 волновая функция не имеет сферической симметрии. Симметрия волновой функции определяется симметрией сферических функций Ylm(θ,φ). Имеет место интересное квантовое явление, когда решение сферически симметричной задачи (потенциал описывает сферически симметричную систему) приводит к состояниям, не обладающим сферической симметрией. Таким образом, симметрия уравнений не обязательно должна отражаться в симметрии каждого отдельно взятого решения этих уравнений, а лишь во всей совокупности этих решений.
Для частицы, находящейся в сферически симметричном потенциале, величина орбитального момента количества движения L:
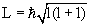 | (4.18) |
Обычно, для упрощения, когда говорят о величине орбитального момента количества движения, называют этой величиной квантовое число l, имея в виду, что между l и L имеется однозначная связь (4.18).
Рис. 4.4 Возможные ориентации вектора 
Так как величина l может принимать только целочисленные значения 0, 1, 2, 3,…, то и орбитальный момент количества движения L квантуется. Например, для частицы с l = 2 момент количества движения
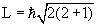
= 6.58·10 -22 √6 МэВ·сек ≈ 2.6·10 — 34 Дж·сек.
Пространственное квантование. Орбитальный момент количества движения является векторной величиной. Так как величина орбитального момента количества движения квантуется, то и направление 

Состояние частицы, находящейся в сферически симметричном поле, полностью описывается тремя квантовыми числами: n, l и m.
Появление квантовых чисел связано со свойствами симметрии системы. Характер этой симметрии определяет возможные значения квантовых чисел. Очевидно, что система, описываемая функцией e im φ , примет прежнее значение только тогда, когда азимутальный угол φ в результате поворота вокруг оси z примет прежнее значение φ. Этому условию функция e im φ удовлетворяет только в случае, когда величина mφ кратна 2π. Т.е. величина m должна иметь целые значения. Так как необходимо учитывать вращение в двух противоположных направлениях и отсутствие вращения, единственно возможными значениями оказываются m = 0, ±1, ±2, … .
4.6. Спин
Спин − собственный момент количества движения частицы. Между значением вектора спина 

 2 = ћ 2 s(s + 1) 2 = ћ 2 s(s + 1) | (4.19) |
В отличие от орбитального квантового числа l, которое может быть лишь целым числом или нулем, спиновое квантовое число s (в дальнейшем просто спин) может быть как целым (включая нуль), так и полуцелым, т. е. s = 0, 1/2, 1, 3/2, 2, 5/2, … , но при этом для каждой элементарной частицы спин может принимать единственное присущее этому типу частиц значение. Так, спины π-мезонов и К-мезонов равны 0. Спины электрона, протона, нейтрино, кварков и их античастиц равны 1/2. Спин фотона равен 1. Бозоны составляют класс частиц с целым значением спина, спин фермионов имеет полуцелое значение. Спин частицы невозможно изменить, также как её заряд или массу. Это её неизменная квантовая характеристика.
Как и в случае других квантовых векторов, проекция вектора спина 
szћ = ±sћ, ±(s − 1)ћ, ±(s − 2)ћ. ±1/2ћ или 0.
Число sz − это квантовое число проекции спина. Максимальная величина sz совпадает с s. Так как спин электрона равен 1/2, то проекция этого спина может принимать лишь два значения sz = ±1/2. Если проекция +1/2, то говорят, что спин направлен вверх, если проекция -1/2, то говорят, что спин направлен вниз.
4.7. Полный момент количества движения
Полный момент количества движения частицы или системы частиц 





Квадрат полного момента имеет значение:

Квантовое число полного момента j, соответствующее сумме двух векторов 

j = l + s, l + s −1. |l − s|
Проекция 
Число значений проекции Jz равно 2j + 1. Если для 

4.8. Квантовые числа
Квантовые числа – это целые или дробные числа, которые определяют все возможные значения физической величины, характеризующей различные квантовые системы – атомы, атомные ядра, кварки и другие частицы.
Таблица квантовых чисел
| n | Радиальное квантовое число. Определяет число узлов волновой функции и энергию системы. n = 1, 2, …, ∞. |
| J, j | Полный угловой момент J и его квантовое число j. Последнее никогда не бывает отрицательным и может быть целым или полуцелым в зависимости от свойств рассматриваемой системы.  2 = ћ 2 j(j + 1). 2 = ћ 2 j(j + 1). |
| L, l | Орбитальный угловой момент L и его квантовое число l. Интерпретация l такая же, как j, но l может принимать только целые значения, включая нуль: l = 0, 1, 2,…. L 2 = ћ 2 l(l + 1). |
| m | Магнитное квантовое число. Проекция полного или орбитального углового момента на выделенную ось (обычно ось z) равна mћ. Для полного момента m = ±j, ±(j-1), …, ±1/2 или 0. Для орбитального m = ± l, ± (l-1), …, ±1, 0. |
| S, s | Спиновый угловой момент S и его квантовое число s. Оно может быть либо положительным целым (включая нуль), либо полуцелым. s – неизменная характеристика частицы определенного типа. S 2 = ћ 2 s(s + 1). |
| sz | Квантовое число проекции спинового момента частицы на выделенную ось. Эта проекция может принимать значения szћ, где sz = ± s, ± (s -1), …, ±1/2 или 0. |
| P или π | Пространственная четность. Характеризует поведение системы при пространственной инверсии  → — → —  (зеркальном отражении). Полная четность частицы Р = π(-1) l , где π – её внутренняя четность, а (-1) l – её орбитальная четность. Внутренние четности кварков положительные, антикварков — отрицательные. (зеркальном отражении). Полная четность частицы Р = π(-1) l , где π – её внутренняя четность, а (-1) l – её орбитальная четность. Внутренние четности кварков положительные, антикварков — отрицательные. |
| I | Изоспин. Характеризует свойство зарядовой инвариантности сильных взаимодействий |
Для обозначения спинового момента часто используют букву J.
Все состояния, в которых может находиться квантовая система, описываются с помощью полного набора квантовых чисел. Так в случае протона в ядре состояние протона описывается с помощью четырех квантовых чисел, соответствующих четырем степеням свободы – трем пространственным координатам и спину. Это
- Радиальное квантовое число n ( 1, 2, …, ∞),
- Орбитальное квантовое число l (0, 1, 2, …),
- Проекция орбитального момента m (± l, ± (l-1), …, ±1, 0),
- Спин протона s =1/2.
Для описания сферически-симметричных систем в квантовой физике используются различные сферически симметричные потенциалы с различной радиальной зависимостью:
- Кулоновский потенциал U = Q/r,
- Прямоугольная потенциальная яма
- Потенциал типа гармонического осциллятора U = kr 2 ,
- Потенциал Вудса-Саксона (с его помощью описываются внутриядерные взаимодействия):
где U0, а и R – положительные константы (R – радиус ядра). Во всех случаях сферически симметричные системы можно описать с помощью набора квантовых чисел n, l, j, jz, однако, в зависимости от радиального вида потенциала энергетический спектр состояний системы будет различным.
Существование сохраняющихся во времени физических величин тесно связано со свойствами симметрии гамильтониана системы. Например, в случае, если квантовая система обладает центральной симметрией U = U(r), то этой системе соответствует сохранение орбитального момента количества движения l и одной из его проекций m. При этом из-за сферической симметрии задачи энергия состояний не будет зависеть от величины m, т. е. состояния будут вырожденными по m.
Наряду с пространственными симметриями, связанными с непрерывными преобразованиями, в квантовой физике существуют и другие симметрии – дискретные. Одной из них является зеркальная симметрия волновой функции относительно инверсии координат (

Система тождественных частиц характеризуется еще одной симметрией – симметрией относительно перестановок тождественных частиц. Эта симметрия определяется свойствами частиц, образующих систему. Системы частиц с целым спином (бозонов) описываются симметричными волновыми функциями, системы частиц с полуцелым спином (фермионов) − антисимметричными волновыми функциями.
Задачи
4.1. Вычислите допустимые уровни энергии электрона, находящегося в одномерной прямоугольной потенциальной яме шириной 10 -8 см, протона, находящегося в потенциальной яме 5 Фм, и шарика массой 1 г, находящегося в потенциальной яме 1 см.
4.2. Рассчитать энергию перехода между состояниями 1s и 2s в атоме водорода.
4.3. Найти значение полного момента j для протона в d-состоянии. Каким будет результат измерения полного момента протона в состоянии 1d5/2?
4.4. Найти полный момент (квантовое число j) системы двух нуклонов в s‑состоянии (l = 0).
4.5. Какие значения может иметь полный момент системы j, если
А. Нейтрон и протон находятся в состояниях с |l,s:j>n = |1, 1 /2: 3 /2>, |l,s:j>p = |1, 1 /2: 3 /2>?
Б. Два нейтрона находятся в состояниях с |l,s:j>1 = |1, 1 /2: 3 /2> и |l,s:j>2 = |1, 1 /2: 3 /2>?
4.6. А) Нейтрон находится в p-состоянии. Найти значения полного момента j и возможные значения проекции момента jz. Каким будет результат измерения орбитального момента частицы в этом состоянии? Б) Рассмотрите задачу А) для протона в d-состоянии.
Ответ: А) j = 3/2, 1/2; jz = ±3/2, ±1/2; L = ћ√ l(l +1) = √ 2 ћ;
Б) j = 5/2, 3/2; jz = ±5/2, ±3/2, ±1/2; L = ћ√ l(l +1) = √ 6 ћ
4.7. А) Частица с собственным моментом s = 3/2 находится в состоянии с орбитальным моментом
l = 2. Найти полный момент частицы j.
Б) Частица с собственным моментом s = 1/2 находится в состоянии с орбитальным моментом
l = 3. Определите полный момент частицы j
Ответ: А) j = 7/2 ÷ 1/2; Б) j = 7/2, 5/2
4.8. Протон и нейтрон находятся в состоянии с относительным орбитальным моментом L = 1. Найти полный момент системы J.
Ответ: J = 0, 1, 2
4.9. На оболочке с квантовым числом n = 1, l = 2 находятся протон и нейтрон. Определить их суммарный полный момент J и его проекцию Jz. Изменится ли результат, если на оболочке n = 1,
l = 2 будут находиться два нейтрона?
4.10. Почему возникают вырожденные состояния?
4.11. Написать оператор Гамильтона 
4.12. Напишите стационарное уравнение Шредингера в сферической системе координат.
4.13. Какие квантовые числа характеризуют частицу в центрально-симметричной потенциальной яме?
4.14. Покажите, что волновые функции ψ = Aexp(kx −ωt) и ψ = Asin(kx −ωt) не удовлетворяют зависящему от времени уравнению Шредингера.
4.15. Покажите, что волновые функции ψ = Ae i(kx −ωt) и ψ = A(cos(kx −ωt) − sin(kx −ωt))удовлетворяют зависящему от времени уравнению Шредингера.
4.16. Частица находится в низшем состоянии n = 1 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L.
А) Рассчитайте вероятность обнаружить частицу в интервале Δx = 0.001L при x = 1 /2L, x = 2 /3L, x = L.
Б) Рассмотрите случай, когда частица находится в состоянии n = 2 при тех же значениях x.
Ответ: А) P(L/2) = 0.002; P(2L/3) = 0.0015; P(L) = 0; Б) P(L/2) = 0; P(2L/3) = 0.0015; P(L) = 0
4.17. Частица находится в состоянии n = 2 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L. Рассчитайте вероятность обнаружить частицу в интервале ( 1 /3L, 2 /3L).
Ответ: P(L/3, 2L/3) = 0.2
4.18. Электрон находится всостонии n = 5 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L. Рассчитайте вероятность обнаружить электрон в области x от 0.2L до 0.5L.
Ответ: P(0.2L, 0.5L) = 0.3
4.19. Электрон находится в бесконечно глубокой одномерной потенциальной яме. Рассчитайте ширину потенциальной ямы, если энергия состояния n = 1 равна 0.1 эВ.
Ответ: L = 1.9 нм
4.20. Рассчитайте средние значения и 2 > для состояний n = 1, 2, 3 в бесконечно глубокой прямоугольной потенциальной яме.
4.21. Что общего и в чем различие в описании атома водорода в теории Шредингера и в модели Бора?
4.22. Почему энергии атома водорода в теории Шредингера не зависят от орбитального квантового числа l?
4.23. Угловой момент характеризуется квантовым числом l = 3. Какие значения могут принимать Lz и L 2 ?
Ответ: Lz = -3ћ, -2ћ. 3ћ; L 2 = 12ћ 2
4.24. Угловой момент характеризуется квантовым числом l = 3. Какие значения могут принимать Lz и L 2 ?
🔍 Видео
Лекция 1 | Квантовая механикаСкачать

Семинар 7. Стационарное уравнение Шредингера. Состояния дискретного спектра. Потенциальные ямы.Скачать

Савельев-Трофимов А. Б. - Введение в квантовую физику - Потенциальная яма (Лекция 6)Скачать

Свешников К.А. - Квантовая теория.Часть 1. Семинары - 11. Задача на яму конечной глубины с δ -ямойСкачать

Эксперимент, который взрывает мозг!Скачать

Квантовая физика Л4. Потенциальная яма конечной глубины. Потенциальные барьеры.Скачать

Рубцов А. Н. - Введение в квантовую физику - Частица в потенциальной ямеСкачать

Движение частицы в потенциальной яме.Скачать

Рубцов А. Н. - Введение в квантовую физику - Волновая функция и уравнение ШредингераСкачать

Шрёдингер и его уравнение — Дэвид Клэри / ПостНаукаСкачать

Частица в одномерной потенциальной ямеСкачать

ВЕБИНАР №5: "Основы работы в MATLAB 5. Частица в потенциальной яме, уравнение Шредингера"Скачать