| Прохождение частиц сквозь потенциальный барьер. Туннельный эффект |   |
Рассмотрим простейший потенциальный барьер прямоугольной формы (рис. 5.4) для одномерного (по оси х) движения частицы. Для потенциального барьера прямоугольной формы высоты U и ширины l можно записать: При данных условиях задачи классическая частица, обладая энергией Е, либо беспрепятственно пройдет над барьером при E > U, либо отразится от него (E U имеется также отличная от нуля вероятность, что частица окажется в области x > l, т.е. проникнет сквозь барьер. Такой вывод следует непосредственно из решения уравнения Шредингера, описывающего движение микрочастицы при данных условиях задачи. Уравнение Шредингера для состояний каждой из выделенных областей имеет вид:
Общее решение этих дифференциальных уравнений:
В данном случае, согласно (5.4.2), Можно показать, что A1 = 1, B3 = 0, тогда, учитывая значение q,получим решение уравнения Шредингера для трех областей в следующем виде:
В области 2 функция (5.4.4) уже не соответствует плоским волнам, распространяющимся в обе стороны, поскольку показатели степени не мнимые, а действительные. Качественный анализ функций Ψ1(x), Ψ2(x), Ψ3(x) показан на рис. 5.4. Из рисунка следует, что волновая функция не равна нулю и внутри барьера, а в области 3, если барьер не очень широк, будет опять иметь вид волн де Бройля с тем же импульсом, т.е. с той же частотой, но с меньшей амплитудой. Таким образом, квантовая механика приводит к принципиально новому квантовому явлению – туннельному эффекту, в результате которого микрообъект может пройти через барьер. Коэффициент прозрачности для барьера прямоугольной формы Для барьера произвольной формы Прохождение частицы сквозь барьер можно пояснить соотношением неопределенностей. Неопределенность импульса на отрезке Δx = l составляет С классической точки зрения прохождение частицы сквозь потенциальный барьер при E Видео:Урок 455. Уравнение ШрёдингераСкачать  4.7. Отражение и туннелирование частицДо сих пор мы имели дело с задачами на связанные состояния. Рассмотрим теперь примеры инфинитного движения частиц, когда они могут уходить на бесконечно большие расстояния. В простейшем случае движения вдоль одной из координатных осей задача рассеяния частиц сводится к задаче взаимодействия частицы с неким потенциальным барьером. Мы рассмотрим несколько типов барьеров простой прямоугольной формы, чтобы выделить характерные особенности этого типа квантовых явлений. Низкий бесконечный барьер Потенциальная энергия имеет вид Слово «низкий» означает, что высота барьера Рис. 4.12. Низкий потенциальный барьер: пунктиром показаны энергия налетающей слева частицы, Решим уравнение Шредингера отдельно для каждой из областей. В области 1 потенциальная энергия равна нулю, и мы получаем то же самое уравнение (4.22), что и для свободной частицы, и его общее решение в уже известном виде где В области 2 уравнение Шредингера имеет вид В этой области меняется кинетическая энергия (и импульс) частицы, и мы должны ввести другой волновой вектор (обозначим его Тогда очевидно, что решение уравнения Шредингера в области 2 будет иметь тот же вид, что и для области 1 с заменой По сути дела, здесь мы снова использовали некое граничное условие, хотя и иное, нежели для задачи о связанном состоянии. Нам осталось определить только амплитуды волн Рис. 4.13. Схематический характер волновой функции частицы для случая низкого потенциального барьера Для этого мы должны вспомнить, что Непрерывность первой производной волновой функции означает выполнение равенства Решение двух полученных уравнений дает Амплитуда падающей волны остается неопределенной: ясно, что она зависит от интенсивности потока частиц! Важны не сами амплитуды, а отношение R квадратов их модулей, то есть интенсивностей отраженной и падающей волн: Величина R называется коэффициентом отражения частицы от низкого барьера. По физическому смыслу это вероятность отражения частицы от барьера. Соответственно, величина
называемая коэффициентом прохождения, определяет вероятность проникновения частицы в правую область. Удивительно, что частица имеет шанс отразиться от низкого барьера и повернуть назад. В классической физике частица всегда (R = 0) проникает за барьер, если ей хватает на это энергии. Например, с точки зрения классической физики электрон с энергией 10 эВ, влетевший в конденсатор с тормозящим полем В 5 эВ, безусловно, преодолеет торможение и продолжит свой путь с уменьшенной энергией равной 5 эВ. В квантовой же теории не равна нулю вероятность того, что электрон отразится от поля конденсатора и повернет назад. Коэффициент отражения можно измерить, направляя поток частиц на барьер и измеряя долю отраженных от него частиц. Высокий бесконечный барьер Потенциальная энергия имеет тот же вид, но энергия частицы меньше высоты барьера: Рис. 4.16. Потенциальный барьер конечной ширины Мы видели, что интенсивность (квадрат модуля амплитуды) волны убывает под барьером и на расстоянии Отношение интенсивностей выходящей и падающей волн называется коэффициентом прозрачности Получая Проникновение частицы сквозь конечный потенциальный барьер возможно в квантовой механике, но категорически запрещено в классической. В самом деле, формально величина становится отрицательной. Дело спасают соотношения неопределенностей. Модуль (мнимой) скорости частицы имеет порядок так что время туннелирования Неопределенность в кинетической энергии Из полученных результатов для коэффициента прозрачности видно, что эффект туннелирования заметен, если Получается, что неопределенность в кинетической энергии частицы под барьером больше самого значения кинетической энергии. Поэтому нельзя утверждать, что под барьером кинетическая энергия отрицательна. Скорее, она «размыта» настолько, что частица может как бы перепрыгнуть не слишком большой барьер. В случае же высокого и широкого барьера «размытость» кинетической энергии должна быть очень велика, что возможно лишь на очень короткое время, за которое частица не успевает проскочить за барьер. Поэтому в этом случае коэффициент прозрачности становится экспоненциально малым. По-другому: туннелирование заметно при ширине барьера порядка длины волны де Бройля. Рис. 4.17. Волновая функция частицы для случая потенциального барьера конечной Барьер произвольной формы можно представить в виде последовательности прямоугольных барьеров; теорема об умножении вероятностей ведет к появлению суммы (интеграла) в экспоненте, так что вместо (4.34) имеем Интеграл берется между точками поворота в которых классическая частица должна изменить направление движения. Пример 1. Электрон находится в одномерной потенциальной яме шириной Рис. 4.18. Частица в потенциальной яме, образованной непроницаемым препятствием и конечным барьером Скорость электрона в яме и за промежуток времени t он подойдет к барьеру При каждом подходе вероятность туннелирования равна D, так что вероятность туннелирования Вероятность Теперь остается подставить численные данные. Для упрощения вычислений имеет смысл отдельно рассчитать коэффициент прозрачности и предэкспоненциальный множитель. Имеем Теперь осталось рассчитать коэффициент прозрачности: Даже по масштабам микромира это время мало: прежде чем электрон просочится сквозь барьер, свет успеет пройти расстояние всего лишь в 0,7 мкм. Прозрачность барьера сильно зависит от энергии частицы в яме и от ширины и высоты барьера. Например, при увеличении ширины барьера в два раза новый коэффициент прозрачности будет равен, как легко догадаться, квадрату старого. Для электрона тогда получится значение Пример 2. Решим предыдущий пример, поместив вместо электрона в ту же потенциальную яму протон. Чтобы не решать аналогичную задачу с самого начала, можно воспользоваться результатами предыдущего примера. Протон массивнее электрона в 1837 раз. В коэффициент прозрачности масса частицы входит под квадратным корнем в показателе экспоненты. При изменении массы в n раз в показателе экспоненты появится множитель и новый коэффициент прозрачности будет равен старому, возведенному в степень Используя данные предыдущего примера, получаем Предэкспоненциальный множитель также умножится на и время жизни протона в потенциальной яме будет равно Получилась столь огромная величина, что протон будет жить в яме вечно: время существования Вселенной «всего» Эти две задачи демонстрируют сильную зависимость проницаемости барьера от массы частицы. Видео:97. Микрочастица в потенциальной ямеСкачать  Уравнение Шредингера. Уравнением движения в квантовой механике, описывающим движение микрочастиц в различных силовых поляхУравнением движения в квантовой механике, описывающим движение микрочастиц в различных силовых полях, должно быть уравнение, из которого вытекали бы волновые свойства частиц. Оно должно быть уравнением относительно волновой функции Ψ(х, у, z, t), так как величина │Ψ│ 2 определяет вероятность пребывания частицы в момент времени в объеме. Основное уравнение сформулированоЭ. Шредингером: уравнения не выводится, а постулируется. Уравнение Шредингера имеет вид: — где ħ=h/(2π), т—масса частицы, Δ—оператор Лапласа, i— мнимая единица,U(x,y,z,t) — потенциальная функция частицы в силовом поле, в котором она движется, Ψ(x,y, z, t) — искомая волновая функция частицы. Уравнение (32.9) является общим уравнением Шредингера. Его также называют уравнением Шредингера, зависящим от времени. Для многих физических явлений, происходящих в микромире, уравнение (33.9) можно упростить, исключив зависимость Ψ от времени, иными словами, найти уравнение Шредингера для стационарных состояний — состояний с фиксированными значениями энергии. Это возможно, если силовое поле, в котором частица движется, стационарно, т. е. функцияU(x,y,z,t) не зависит явно от времени и имеет смысл потенциальной энергии. ∆Ψ + Уравнение (33.10) называется уравнением Шредингера для стационарных состояний. В это уравнение в качестве параметра входит полная энергия Е частицы. Решение уравнения имеет место не при любых значениях параметра Е, а лишь при определенном наборе, характерном для данной задачи. Эти значения энергии называются собственными. Собственные значения Е могут образовывать как непрерывный и дискретный ряд. 33.5. Частица в одномерной прямоугольной «потенциальной яме с бесконечно высокими «стенками» Свободная частица — частица, движущаяся в отсутствие внешних полей. Так как на свободную частицу (пусть она движется вдоль оси х) силы не действуют, то потенциальная энергия частицы U (х) = соnstи ее можно принять равной нулю. Тогда полная энергия частицы совпадает с ее кинетической энергией. Энергия свободной частицы может принимать любые значения, т. е. ее энергетический спектр является непрерывным. Свободная квантовая частица описывается плоской монохроматической волной де Бройля, и все положения свободной частицы в пространстве являются равновероятными. где l — ширина «ямы», а энергия отсчитывается от ее дна (рис.33.1). Уравнение Шредингера для стационарных состояний в случае одномерной задачи запишется в виде По условию задачи (бесконечно высокие «стенки»), частица не проникает за пределы «ямы», поэтому вероятность ее обнаружения (а следовательно, и волновая функция) за пределами «ямы» равна нулю. На границах «ямы» (при х=0 и х=l) непрерывная волновая функция также должна обращаться в нуль. Следовательно, граничные условия в данном случае имеют вид В пределах «ямы» уравнение Шредингера сведется к уравнению Стационарное уравнение Шредингера, описывающее движение частицы в «потенциальной яме» с бесконечно высокими «стенками», удовлетворяется только при собственных значениях Еп зависящих от целого числа п. Еп= Следовательно, энергия Еп частицы в «потенциальной яме» с бесконечно высокими «стенками» принимает лишь определенные дискретные значения, т.е. квантуется. Квантованные значения энергии Еп — называются уровнями энергии, а число п, определяющее энергетические уровни частицы, называется главным квантовым числом. Таким образом, микрочастица в «потенциальной яме» с бесконечно высокими «стенками» может находиться только на определенном энергетическом уровне Еп, или, как говорят, частица находится в квантовом состоянии п. Частица «в потенциальной яме» с бесконечно высокими «стенками» не может иметь энергию меньшую, чем минимальная энергия, равная Туннельный эффект Рассмотрим простейший потенциальный барьер прямоугольной формы (рис.33.2.а) для одномерного (по оси х) движения частицы. Для потенциального барьера прямоугольной формы высоты U ширины l можем записать 0, х 1(для области 3), Таким образом, квантовая механика приводит к специфическому квантовому явлению, получившему название туннельного эффекта, в результате которого микрообъект может «пройти» сквозь потенциальный барьер. Для описання туннельного эффекта используют понятие коэффициента прозрачности D потенциального барьера, определяемого как отношение плотности потока прошедших частиц к плотности потока падающих. Решение уравнения Шредингера для прямоугольной потенциального барьера дает формулу для коэффициента прозрачности: D = D0 exp( — где U — высота потенциального барьера, Е — энергия частицы, l — ширина барьера, D0— постоянный множитель, который можно приравнять единице. Из этого выражения следует, что D сильно зависит от массы частицы, ширины барьера и от (U — Е); чем шире барьер, тем меньше вероятность прохождения сквозь него частицы. С классической точки зрения прохождение частицы сквозь потенциальный барьер при Е h/l. Связанная с этим разбросом в значениях импульса кинетическая энергия может сказаться достаточной для того, чтобы полная энергия частицы сказалась больше потенциальной. Туннельное прохождение сквозь потенциальный барьер лежит в основе многих явлений физики твердого тела (например, явления в контактном слое на границе двух полупроводников), атомной и ядерной физики (например, a-распад, протекание термоядерных реакций). 🔍 ВидеоВолновая функция (видео 5) | Квантовая физика | ФизикаСкачать  98. Туннельный эффектСкачать  Квантовая механика 41 - Уравнение Шредингера. Гамильтониан.Скачать  Консультация по квантовой механике. Часть 5. "Волновая функция. Уравнение Шредингера"Скачать  Частица в одномерной потенциальной ямеСкачать  Урок 456. Движение микрообъекта в одномерной бесконечно глубокой потенциальной ямеСкачать  Елютин П. В. - Квантовая теория I - Задача о прохождении потенциального барьераСкачать  Семинары №4 и 5. Уравнение Шредингера. Ямы и барьерыСкачать  5_4. Уравнение ШредингераСкачать  Уравнение Шрёдингера. Туннельный эффект. (3/15). Ципенюк Ю. М (МФТИ).Скачать  Урок 454. Понятие о волновой функцииСкачать  Туннельный потенциальный барьер.Скачать  Семинар 8. Потенциальные барьерыСкачать  Лекция №4 "Волновая функция. Уравнение Шредингера" (Гавриков А.В.)Скачать  Структура материи 6: уравнение Шрёдингера. Зачем нужна квантовая механика – Виталий Бейлин | НаучпопСкачать  О прохождении потенциального барьераСкачать  Классические уравнения | уравнение Шрёдингера (координатное представление) | простейший выводСкачать  Классические уравнения | одномерное стационарное уравнение Шрёдингера | беск. потенц. яма | 1Скачать  |



 ,
, .
.
 – мнимое число, где
– мнимое число, где 

 .
. .
. Связанная с этим разбросом кинетическая энергия
Связанная с этим разбросом кинетическая энергия  может оказаться достаточной для того, чтобы полная энергия оказалась больше потенциальной и частица может пройти через барьер.
может оказаться достаточной для того, чтобы полная энергия оказалась больше потенциальной и частица может пройти через барьер.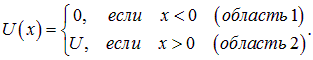
 меньше энергии частицы
меньше энергии частицы 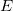 (рис. 4.12).
(рис. 4.12).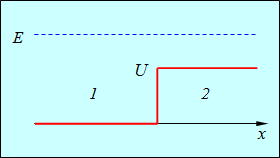
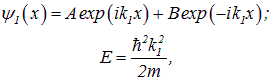
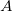 и
и 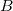 — амплитуды падающей и отраженной волн соответственно.
— амплитуды падающей и отраженной волн соответственно.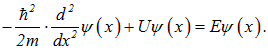
 в отличие от прежнего
в отличие от прежнего  )
)
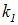 на
на 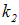 . Однако из физических соображений ясно, что в области 2 не может быть волны, распространяющейся справа налево (в бесконечно удаленной точке ей не от чего отражаться). Поэтому волновая функция в этой области соответствует прямой волне
. Однако из физических соображений ясно, что в области 2 не может быть волны, распространяющейся справа налево (в бесконечно удаленной точке ей не от чего отражаться). Поэтому волновая функция в этой области соответствует прямой волне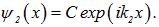
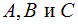 .
.
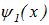 и
и  — значения одной волновой функции в разных пространственных областях. Эта волновая функция должна быть непрерывна вместе со своей первой производной по переменной x. Непрерывность функции в точке x=0 означает, что должно выполняться условие
— значения одной волновой функции в разных пространственных областях. Эта волновая функция должна быть непрерывна вместе со своей первой производной по переменной x. Непрерывность функции в точке x=0 означает, что должно выполняться условие

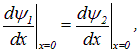
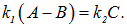
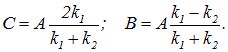
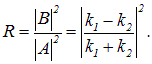
 ,
,
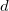 становится меньше в
становится меньше в 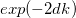 раз. Но в этой точке барьер кончается, так что волна выйдет на свободу справа от барьера с уменьшенной амплитудой.
раз. Но в этой точке барьер кончается, так что волна выйдет на свободу справа от барьера с уменьшенной амплитудой. (он же равен вероятности прохождения через барьер). Из приведенных выше рассуждений следует приближенное выражение для
(он же равен вероятности прохождения через барьер). Из приведенных выше рассуждений следует приближенное выражение для 
 вклад таких процессов невелик и сделанное приближение оправдано.
вклад таких процессов невелик и сделанное приближение оправдано. играет роль импульса (мнимого), так что кинетическая энергия
играет роль импульса (мнимого), так что кинетическая энергия

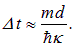
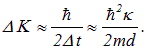




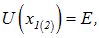
 (рис. 4.18) и имеет энергию
(рис. 4.18) и имеет энергию  . С одной стороны ямы потенциальная энергия
. С одной стороны ямы потенциальная энергия  бесконечна, а с другой стороны выйти из ямы электрону мешает потенциальный барьер высотой
бесконечна, а с другой стороны выйти из ямы электрону мешает потенциальный барьер высотой  и шириной
и шириной 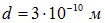 . Оценим время жизни
. Оценим время жизни 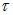 электрона в яме.
электрона в яме.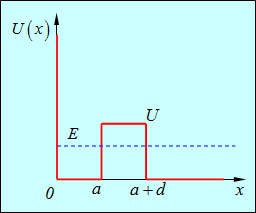

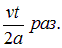
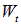 за время t равна
за время t равна
 увеличивается с ростом промежутка времени t. При некотором значении
увеличивается с ростом промежутка времени t. При некотором значении  вероятность туннелирования станет равной единице, и электрон вырвется из ямы. Отсюда получаем для времени жизни электрона в яме оценку:
вероятность туннелирования станет равной единице, и электрон вырвется из ямы. Отсюда получаем для времени жизни электрона в яме оценку: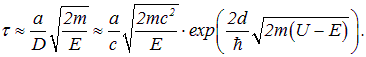


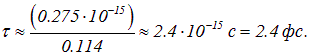
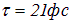 . Это и объясняет отсутствие туннелирования в обычном мире с его высокими и широкими потенциальными барьерами.
. Это и объясняет отсутствие туннелирования в обычном мире с его высокими и широкими потенциальными барьерами.




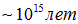 .
.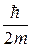 ΔΨ + U(x,y, z, t)Ψ = iħ
ΔΨ + U(x,y, z, t)Ψ = iħ 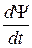 , (33.9)
, (33.9)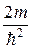 (E—U)Ψ = 0. (33.10)
(E—U)Ψ = 0. (33.10) Проведем качественный анализ решений уравнения Шредингера применительно к свободной частице в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками» (рис.33.1). Такая «яма» описывается потенциальной энергией вида (для простоты принимаем, что частица движется вдоль оси х)
Проведем качественный анализ решений уравнения Шредингера применительно к свободной частице в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками» (рис.33.1). Такая «яма» описывается потенциальной энергией вида (для простоты принимаем, что частица движется вдоль оси х)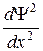 +
+ 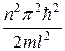 ,( n= 1, 2, 3, …).(33.15)
,( n= 1, 2, 3, …).(33.15)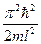 .
. При данных условиях задачи классическая частица, обладая энергией Е, либо беспрепятственно пройдет над барьером (при Е> U), либо отразится от него (при Е U, имеется отличная от нуля вероятность, что частица отразится от барьера и будет двигаться в обратную сторону. При Е l, т. е. проникает сквозь барьер. Подобные, казалось бы, парадоксальные выводы следуют непосредственно из уравнения Шредингера, описывающего микрочастицы при условиях данной задачи.
При данных условиях задачи классическая частица, обладая энергией Е, либо беспрепятственно пройдет над барьером (при Е> U), либо отразится от него (при Е U, имеется отличная от нуля вероятность, что частица отразится от барьера и будет двигаться в обратную сторону. При Е l, т. е. проникает сквозь барьер. Подобные, казалось бы, парадоксальные выводы следуют непосредственно из уравнения Шредингера, описывающего микрочастицы при условиях данной задачи.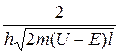 ), (33.16)
), (33.16)