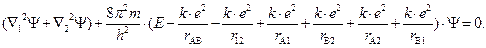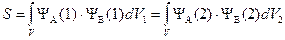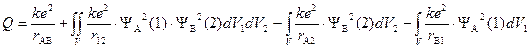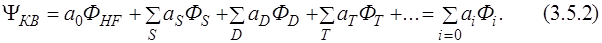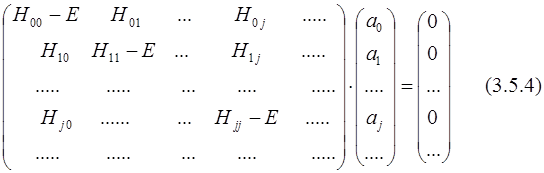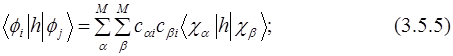Основы метода ВС разработали в 1927 г. Вальтер Гайтлер (Heitler) и Фриц Лондон (London). Модельной частицей для этого метода является молекула водорода Н2. При построении волновой функции молекулы в методе валентных связей считается, что: 1)атомы в молекуле сохраняют свою индивидуальность – каждый электрон принадлежит ядру своего атома, 2) известны волновые функции электронов атома А (YА) и атома В (YВ) –атомные орбитали, 3) считается, что частицы (электроны и ядра атомов) неразличимы.
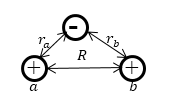
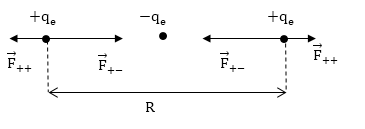
Уравнение Шрёдингера для молекулы водорода. Составим уравнение Шрёдингера для молекулы водорода. Входящая в него потенциальная энергия включает в себя сумму энергий электростатического взаимодействия всех частиц между собой (двух электронов -e и двух ядер +e). Из рис. 3.3 видно, что суммарная потенциальная энергия складывается из двух положительных членов: энергии отталкивания электронов и ядер между собой и четырех отрицательных – энергий притяжения электронов к ядрам:
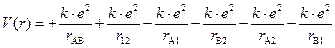

Рис. 3‑3 Схема электростатического взаимодействия электронов и ядер в молекуле водорода
Таким образом, уравнение Шрёдингера для молекулы водорода имеет вид
Аналитическое решение данного уравнения практически невозможно, поэтому нахождение энергии химической связи DE(r) и волновой функции электронов, показывающей распределение электронной плотности в молекуле, производят приближенным методом.
Функция первого приближения. Поскольку вероятность нахождения электрона в элементарном объеме пропорциональна Y-функции, а по условиям метода ВС атомы при образовании связи сохраняют свои атомные орбитали, то в первом приближении функция, описывающая состояние электронов в молекуле водорода, может быть представлена как произведение волновых функций электронов в отдельных изолированных атомах водорода:
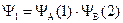
где Y1 – функция, описывающая состояния электронов в молекуле водорода; YА(1) – функция, описывающая состояния электрона 1, принадлежащего атому А (Y1s – функция основного состояния атома водорода); YВ(2) функция, описывающая состояния электрона 2, принадлежащего атому В (Y1s).
Поскольку электроны и ядра атомов принципиально неразличимы, то безразлично, какой из них будет находиться у определенного ядра. Поэтому необходимо составить и вторую функцию:
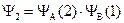
Первая функция рассматривает 1 электрон как принадлежащий атому А, а 2 – атому В, вторая функция, наоборот, считает, что 2 электрон принадлежит атому А, а 1 – атому В. Обе функции являются решениями уравнения Шрёдингера. Для простоты изложения нормировочные множители приняты равными единице.
Расчет с использованием этих функций качественно правильно описывал молекулу водорода, но величины энергии и длины связи сильно отличались от величин, определенных экспериментально.
Более точным приближением к истинной волновой функции явилась линейная комбинация первой и второй функции:
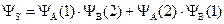
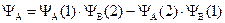
Физический смысл этих двух функций заключается в следующем: YS – симметричная функция – соответствует случаю, когда электроны в молекуле водорода имеют разные по знаку значения спинового квантового числа, – спины электронов антипараллельны. YА – антисимметричная функция – описывает состояние, когда оба электрона имеют одинаковое значение спинового числа – спины электронов параллельны.
Изменение энергии системы двух взаимодействующих атомов водорода описывается выражением
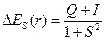
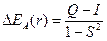
Q – «кулоновский интеграл», характеризующий изменение энергии системы вследствие электростатического взаимодействия электронов и ядер между собой. I – «обменный интеграл», интеграл, характеризующий понижение энергии системы вследствие неразличимости электронов; S – «интеграл перекрывания», характеризующий изменение энергии системы вследствие перекрывания атомных орбиталей.
Для выяснения физического смысла этих интегралов проанализируем их выражения.
характеризует область пространства перекрывания атомных орбиталей.
показывает изменение энергии системы в результате отталкивания ядер друг от друга (первый член суммы), электронов (второй член) и притяжения электронов к ядрам «несвоего атома» (третий и четвертый члены). Последние два интеграла равны между собой, поскольку атомы одинаковы. Физический смысл интегралов очевиден: yi 2 dVj – вероятность нахождения j-электрона в элементарном объеме пространства, e×yi 2 dVj – величина заряда. Согласно закону Кулона энергия электростатического взаимодействия прямо пропорциональна произведению величины зарядов и обратно пропорциональна расстоянию между ними.
Энергия притяжения электронов к ядрам «своего атома» – энергия невзаимодействующих атомов (E0) – в энергии химической связи не учитывается (полная энергия молекулы водорода E = 2×E0+DE(r)).
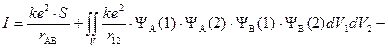
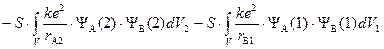
S – «интеграл перекрывания».
«Обменный интеграл» похож на «кулоновский», но вместо квадрата волновой функции для данного электрона стоит произведение волновых функций разных атомов, что придает ему достаточно абстрактный характер — «неклассическое электростатическое взаимодействие». Энергия системы изменяется вследствие неразличимости электронов, то есть возможность замены одного электрона на другой приводит к изменению энергии системы.
На расстояниях r®¥ кулоновский, обменный интегралы и интеграл перекрывания стремятся к нулю: Q®0, I®0 и S®0. На расстояниях, близких к длине связи, кулоновский и обменный интегралы отрицательны Q
Дата добавления: 2017-02-20 ; просмотров: 701 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

Молекулярный ион водорода. Молекула водорода
Вы будете перенаправлены на Автор24
Видео:Урок 459. Обзор квантовой теории атома водородаСкачать

Ион молекулы водорода
Физическое описание молекулы принципиально не отличается от физики атома. Но уравнение Шредингера даже для самого простого случая (системы молекулярного типа из трех частиц) невозможно решить аналитически.
Простейшей системой молекулярного типа из трех частиц является ион молекулы водорода ($H^+_2$). Он в своем составе имеет: два протона и один электрон (рис.1). В теории, молекулярный ион водорода исполняет роль, подобную роли атома водорода в атомной физике. Поэтому необходимо иметь для него хотя бы приблизительное решение уравнения Шредингера. Для этого применяют адиабатическое приближение (приближение Борна — Оппенгеймера), в основу которого положено большое различие между массами электронов и ядер. При этом ядра считают неподвижными, а электроны рассматривают как перемещающиеся в стационарном поле, которое создают ядра. Применяя данное приближение, получают решения для конкретных конформаций молекулы (пространственных расположений атомов в молекуле). Для молекул, которые состоят из двух атомов, конформации определены расстояниями между ядрами. Для каждой конформации появляется возможность найти потенциальную энергию молекулы и связать ее с параметрами, которые характеризуют конформацию молекулы. При этом минимум потенциальной энергии соответствует равновесной конформации молекулы.
Рисунок 1. Ион молекулы водорода. Автор24 — интернет-биржа студенческих работ
В адиабатическом приближении уравнение Шредингера для иона молекулы водорода можно записать как:
где $r_a$, $r_b$ — соответствуют обозначениям рис.1. Для того чтобы разделить переменные в уравнении (1) переходят к эллиптическим координатам ($xi ,eta ,varphi $), которые связывают с $r_a$, $r_b$ при помощи формул:
Задача для иона водорода имеет аксиальную симметрию и ее решение от азимутального угла вокруг оси молекулы ($varphi )$ не зависит.
Решение уравнения Шредингера важно для того, чтобы иметь возможность сравнить результаты опытов и убедиться в возможности применения квантовой механики к молекулярным системам. Кроме того это решение дает возможность проверить справедливость адиабатического приближения, которое используют в теории молекул.
Готовые работы на аналогичную тему
При больших расстояниях $R$ около ядра $a$ при выполнении условия:
уравнение (1) переходит в уравнение для атома водорода с ядром в точке $a$. Аналогично можно рассуждать относительно точки $b$. Волновая функция, которая является решением уравнения Шредингера и существенно отлична от нуля только около точек $a и b$. Между данными точками $Psi$ — функция практически равна нулю. При этом перекрытия плотностей электронного облака между протонами нет, ковалентной связи не появляется.
При сближении протонов распределение электронной плотности около них изменяется мало, а между протонами электронная плотность значительно отличается от нуля, причем это связано с симметрией волновой функции. Если волновая функция симметрична, то распределение электронной плотности между протонами не имеет узлов и растет, что приводит к появлению ковалентной связи.
Суммарная энергия системы состоит из отрицательной энергии связи электрона ($E_e$) и положительной энергии взаимодействия протонов ($E_p$). Если $R$ велико, то $E_eapprox -13,6 эВ$, $E_papprox 0.$ При $Rto 0$ протоны сливаются друг с другом, и система становится ионом гелия ($^+$).
Видео:Урок 455. Уравнение ШрёдингераСкачать

Молекула водорода
Молекула водорода состоит из двух протонов и двух электронов. Это одна из простейших молекул. Обозначим протоны буквами: $a и b$, а электроны цифрами 1и 2. В том случае, если расстояния между протонами небольшие, то волновые функции сильно перекрываются. Это значит, что каждый электрон принадлежит обоим атомам (между атомами существует обмен электронами). Так появляются обменные силы, которые создают ковалентную связь.
Теоретическая задача в данном случае состоит в нахождении энергии взаимодействия как функции расстояния между протонами. Эта задача часто решается при помощи теории возмущений. В качестве невозмущенного состояния используют основное состояние двух невзаимодействующих атомов водорода.
Для объяснения принципов создания связи между атомами в молекуле водорода положены законы квантовой механики. В первую очередь учитывается волновой характер электрона, который говорит о существовании вероятности обнаружения электрона в непосредственной близости от ядра. В самом простом случае (s- состояние электрона) распределение вероятности имеет сферическую симметрию: так называемое электронное облако является сферой определенного радиуса. Помимо этого учитывается принципиальная неразличимость электронов. Следовательно, если электроны обменяются местами, то в состоянии молекулы водорода ничего не изменится. Такой обмен может состояться только, если ядра атомов в молекуле находятся на малом расстоянии и электронные облака атомов перекрываются. Слияние районов, где могут быть локализованы оба электрона в молекуле водорода, и обозначает появление между ними квантовмеханического обменного взаимодействия. Так, каждый из электронов в молекуле $H_2$ принадлежит то одному, то другому ядру.
Два атома водорода притягиваются и создают молекулу, в том случае, если спины электронов в атомах антипараллельны. В таком случае энергия взаимодействия имеет минимум, если расстояние между протонами составляет порядка Боровского радиуса. Если спины атомов $H$ параллельны, то между атомами на любых расстояниях действуют силы отталкивания, и молекула образоваться не может. Полный спин молекулы водорода равен нулю. Замкнутые оболочки атомов отталкиваются всегда.
Опыты показали, что молекула водорода диамагнитна, так как при отсутствии у молекулы орбитального магнитного момента и при наличии взаимно компенсированных спинах суммарный магнитный момент молекулы равен нулю.
Задание: Связанное состояние из двух протонов может образовываться при имеющемся одном электроне. Подобным состоянием является ион молекулы водорода ($H^+_2$). В таком случае невозможно говорить об обменном взаимодействии. Поясните на классической модели, как реализуется такая связь.
В ионе молекулы водорода связь осуществляется единственным электроном, который принадлежит обоим ядрам в равной мере. Как возникают силы притяжения между ядрами, рассмотрим на классическом примере (рис.2).
Рисунок 2. Молекулярный ион водорода. Молекула водорода. Автор24 — интернет-биржа студенческих работ
На рис 2. электрон, несущий отрицательный заряд находится посередине между положительными протонами. Ядра (протоны) отталкиваются друг от друга с силой:
При этом ядро и электрон притягиваются друг к другу с силой:
Из формул (1.1) и (1.2) очевидно, что $F_ >F_$. Данный пример показывает только причину возникновения сил притяжения, но классическая физика не может объяснить является ли такое связанное состояние устойчивым.
Задание: Объясните, почему только в синглетном состоянии атомов возможно образование молекулы, в триплетном состоянии молекула образовываться не может.
Почему атомы в синглетном и триплетном состояниях ведут себя по разному можно понять исходя из симметрии волновых функций. В синглетном состоянии спиновая волновая функция антисимметрична, в нулевом приближении получается симметричная пространственная функция с разделяющимися переменными:
где $C_s$ — постоянная нормировки, $Psi_a$ — волновая функция электрона, если он принадлежит ядру $a$, $Psi_b$ — волновая функция электрона, если он принадлежит ядру $b$. (Функции $Psi_a$ и $Psi_b$ считают разными, но они аналитически представлены одинаковыми выражениями).
В триплетном состоянии спиновая волновая функция симметрична, в нулевом приближении получается антисимметричная пространственная функция с разделяющимися переменными:
где $C_a$ — постоянная нормировки.
В триплетном состоянии антисимметричная пространственная волновая функция имеет узел в плоскости симметрии, которая проходит посередине между ядрами перпендикулярно прямой, которая их соединяет. Это происходит из-за тождественности электронов:
Эта же причина служит тому, что в синглетном состоянии пространственная волновая функция в той же плоскости симметрии обращается в максимум. Следовательно, в синглетном состоянии плотность вероятности локализации электрона около данной плоскости велика. В триплетном состоянии этаже плотность вероятности стремится к нулю.
В результате в синглетном состоянии начиная с некоторого расстояния кулоновское отталкивание ядер, компенсируется действием электронов противоположного направления (отталкивание изменяется на притяжение). Отрицательный заряд электронов, который появляется между ядрами, стягивает их, при этом возникает связанное состояние. В триплетном состоянии посередине между ядрами компенсирующего действия электронов мало, поскольку мала вероятность нахождения электронов в этой области.
На малых расстояниях (меньше Боровского радиуса) ядра всегда отталкиваются не зависимо от состояния. При этом отталкиваются и протоны (между собой) и электроны (между собой).
Видео:ЧК МИФ 5 2 01 01 L4 Уравнение Шредингера для атома водородаСкачать

Решение уравнения Шрёдингера для молекулы водорода, для гомоядерных и гетероядерных двухатомных молекул. Молекулярные термы
Электронные состояния атомов нумеруют с помощью квантового числа L , задающего квадрат суммарного углового момента электронов. В отсутствии внешних полей все направления равноправны, и состояния с разными проекциями момента на ось z (напомним, что таких состояний ровно 2L+1) имеют одинаковую энергию. В результате энергетические уровни 2L+1-кратно вырождены. Обычно значения L задают буквами, как в атоме водорода, где состояния обозначаются как s, p, d… при значениях квантового числа l , описывающих угловой момент электрона, 0, 1, 2, . соответственно. Как принято в квантовой механике, для состояний многоэлектронных систем используются заглавные буквы: состояниям с L = 0, 1, 2. соответствуют символы S, P, D,…латинского алфавита.
Атом обладает очень высокой сферической симметрией и классификация состояний по угловому моменту – это классификация по типам симметрии относительно всевозможных поворотов. Кроме поворотов группа симметрии атома включает инверсию. При инверсии волновая функция может либо сохранять, либо менять знак, т.е. состояния обладают определенной четностью. Четность указывают не всегда, причем раньше её указывали нижними индексами g или u (от немецких слов gerade и ungerade), а потом стали использовать верхние индексы «o» (от английского слова odd) для указания только нечетных состояний. В верхнем левом углу символа состояния указывают спиновую мультиплетность – число 2S+1. Принято называть состояния с заданной мультиплетностью 2S+1 синглетными (S = 0, 2S+1 = 1), триплетными (S = 1, 2S+1 = 3), квинтетными (S = 1, 2S+1 = 3) и т.д. (при четном числе электронов в атоме и, следовательно, целом значении S ) и дублетными (S = 1/2, 2S+1 = 2), квартетными (S = 3/2, 2S+1 = 4), секстетными (S = 5/2, 2S+1 = 6). (при нечетном числе электронов). Состояние атома с данными L и S вырождено (2S+1)×(2L+1) раз.
Например, низшие по энергии состояния атома азота – это 4 S o , 2 D o , 2 P o , 4 P, 2 P, . Cимвол состояния 2 D o , например, произносится так: «нечетное дублетное D-состояние». Это состояние имеет кратность вырождения 2×(2×2+1) = 10 , а четное квартетное Р-состояние (4P) – 4×3 = 12.
При заметном спин-орбитальном взаимодействии имеет смысл лишь суммарный электронный момент J = L+S . Число J, нумерующее собственные значения квадрата суммарного момента указывают обычно справа внизу символа состояния. Такое состояние вырождено 2J+1 раз.Для тяжелых атомов иногда указывают только J (цифрой) и чётность состояния. Индексы i и r, используемые иногда в символах состояний, указывают на заполнение валентной оболочки больше, или меньше чем на половину. Одну и ту же конфигурацию, например, 1s 2 2s 2 2p 2 имеют принципиально разные электронные состояния 3 P0, 3 P1, 3 P2, 1 D2 , 1 S0 (приведены в порядке возрастания энергии, определяемом иногда правилами Гунда) атома С. Электронные термы этих состояний составляют соответственно 0, 16.40, 43.40, 10192.63, 21648,01 см-1 (терм низшего по энергии, основного состояния по традиции принимается равным нулю). Напомним также, что задание волновой функции электронной конфигурацией имеет смысл лишь в контексте приближенных методов типа Хартри–Фока или функционала плотности.
Двухатомная молекула обладает довольно высокой симметрией. Два ядра лежат на оси z и задают аксиально-симметричный потенциал, в котором движутся электроны. Группа симметрии ядерной конфигурации включает операции поворотов вокруг осисимметрии С ∞ и отражения в любых плоскостях симметрии σv, содержащих эту ось. Такая группа симметрии – С ∞v – соответствует гетероядерным молекулам. В случае гомоядерных молекул имеется ещё центр инверсии i, а также другие элементы симметрии, вызванные наличием i: любые оси симметрии второго порядка, проходящие через центр и перпендикулярные оси z, а также плоскость симметрии σh , перпендикулярная оси z. Эти молекулыотносятся к группе симметрии D∞h. Осевая симметрия позволяет классифицировать электронные состояния с помощью оператора проекции суммарного электронного углового момента Lz . Собственные значения этого оператора задаются числами hLz (Lz =0, ±1, . ) и, с классической точки зрения, описывают вращение электронов вокруг оси z. Поскольку вращению по- и против часовой стрелки должна отвечать одинаковая энергия, энергии состояний с одинаковыми значениями Λ=|Lz| , но разными знаками Lz, должны совпадать, т.е. эти состояния двукратно вырождены (если не принимается во внимание спин-орбитальное взаимодействие). Электронные состояния двухатомных молекул классифицируются по значениям квантовых чисел Λ и чисел, описывающих квадрат спина (S) и проекцию спина на ось z (Σ). При этом используют буквенные обозначения, похожие на обозначения состояний с разным угловым моментом для атомов. Если описывают симметрию волновых функций одноэлектронных состояний (т.е. орбиталей) с Λ = 0, 1, 2, 3,…, используют буквы греческого алфавита : σ, π, δ, ϕ… Для многоэлектронных систем используются заглавные буквы: Σ, Π, Δ, Φ.
Примечание: Соответствие s – σ, p – π, d – δ, f – Φ очевидно, но далее символы следуют в соответствии с греческим алфавитом: при Λ = 4, например, орбитали имеют тип ψ, а многоэлектронные функции – Ψ. В случае Σ-состояний возможно различие в волновых функции относительно отражения в плоскости σv : волновые функции состояний типа Σ+ не изменяются, а в случае состояний Σ– меняют знак на противоположный (для орбиталей в трехмерном пространстве эту четность не указывают, так как нельзя построить ненулевую орбиталь σ–типа). При Λ > 0 операции отражения σv соответствует уже рассмотренное изменение направления вращения. Для гомоядерных систем надо еще указать, меняет или не меняет знак функция при инверсии. Нечетные и четные функции обозначают нижними правыми индексами u или g соответственно. В верхнем левом углу символа состояния указывают спиновую мультиплетность – число 2S+1. Основное, самое нижнее по энергии электронное состояние обозначается буквой Х, следующие по энергии – заглавными буквами латинского алфавита А, В, С…, если состояния имеют ту же мультиплетность 2S+1, что и основное, или малыми буквами a, b, c,…, если они отличаются по спину; иногда используют штрихи при буквенных символах. Отметим, что в этой номенклатуре есть и исторически сложившиеся исключения. Дело в том, что нумерация электронных состояний «по имени» складывалась в том порядке, в котором эти состояния открывались (чаще всего в этих случаях используются символы состояния со штрихами).
Вырождение состояний с разными проекциями спина происходит, лишь, если в молекуле отсутствует или очень мало спин-орбитальное взаимодействие. Если оно велико, (что типично для молекул с тяжелыми ядрами), то электронное состояние молекулы характеризуется не только числом Λ, но и числом Ω, равным модулю проекции суммарного электронного момента импульса на ось: Ω=|Lz+Σ|. Например, для состояния типа 2Π возможные значения Ω могут быть равны 3/2 (при Lz =1, Σ = +1/2, или при Lz = –1, Σ = –1/2) и 1/2 (при Lz =1, Σ = –1/2 или при Lz = –1, Σ = +1/2 ). Такие состояния обозначают дополнительным символом Ω в правом нижнем углу (или в скобках).
Среднее значение электронного гамильтониана в электронном состоянии Ψn – это электронная энергия En. Она то и играет роль потенциальной энергии при изучении движений ядер с помощью ядерного уравнения Шредингера. Для двухатомной молекулы это уравнение можно записать так: ( формула)
http://www.chem.msu.su/rus/teaching/kovba-pupyshev/kovba-pupyshev-spectra.pdf(стр.12 ) Здесь ψn,k – ядерная волновая функция, ε
n,k – энергетические уровни молекулы, а символы n и k использованы для указания состояний электронов (n) и состояний ядер (k).
Ядерное уравнение Шредингера описывает поведение двух ядер под действием потенциала En , зависящего лишь от взаимного расположения ядер в пространстве. Из курса физики известно, что подобные «задачи двух тел» можно решить, используя радиус-вектор центра масс и вектор относительного положения ядер: ( формула)
В этом случае ядерный гамильтониан оказывается суммой двух гамильтонианов, один из которых – кинетическая энергия центра масс, зависящая лишь от координат центра масс. Этот оператор описывает свободное движение центра масс молекулы (соответствующая волновая функция – это , где k – волновой вектор, показывающий направление импульса центра масс, а энергия поступательного движения центра масс равна (формула) . Второй гамильтониан зависит только от переменных
относительного движения R; информация о строении молекулы в основном содержится именно в этом гамильтониане. Поскольку переменные разделяются, функция стационарного состояний будет произведением волновых функций свободного движения центра масс и функции относительного движения частиц, зависящей лишь от R, так что, изучая переходы в молекуле, мы будем рассматривать только изменения этой функции. В классической модели это построение отвечает разбиению энергии молекулы на поступательную и внутреннюю.
После отделения переменных центра масс ядерное уравнение Шредингера (7.1) будет иметь вид: ( формула) (7.2),
где R = Ra– Rb, μ – приведенная масса : (формула). В сферических координатах (R,θ,ϕ) оператор Гамильтона в ядерном уравнении запишется как: (формула)(7.3).
Первое слагаемое здесь отвечает кинетической энергии для радиальных (колебательных) движений, а второе имеет вид кинетической энергии вращения. μR 2 – это момент инерции ядер относительно центра масс, а LR 2 – зависящий лишь от полярных углов оператор квадрата углового момента ядер. Если использовать метод разделения переменных и представить волновую функцию ψ(R) в виде произведения функции χ(R), зависящей только от R, и функции Y(θ,ϕ), зависящей лишь от полярных углов (эти функции известны из квантовой механики как сферические гармоники), то нетрудно выписать уравнение для функции χ(R).
К сожалению, в таком понятном рассуждении есть существенный недостаток. В отсутствие внешних полей должен сохраняться полныймомент J всей молекулы как целого, а не только угловой момент ядер. Даже если не учитывать дающий очень малый вклад в энергию ядерный спин, то надо было бы полагать, что сохраняется не LR , а J = L + S + LR. Тем не менее, мы заменим оператор квадрата момента в ядерномуравнении на оператор J 2 (например, ссылаясь на то, что массы ядер намного больше, чем у электронов, а электроны улетают от ядер не слишком далеко. Кроме того, если проделать весьма громоздкие выкладки, приводимое ниже уравнение для радиальной функции тоже получится, но со слегка модифицированным потенциалом). Поскольку момент сохраняется, все состояния молекулы можно классифицировать по собственным значениям оператора квадрата полного момента J 2 , а они равны. Тогда ядерное уравнение (7.1), будет зависеть только от радиальной координаты (такое ядерное уравнение часто называют радиальным уравнением) и запишется, как: (формула) (7.4).
Энергия молекулы εn,J,v определяется номером электронного состояния n, вращательным квантовым числом J и номером колебательного состояния v . Напомним, что одним и тем же квадратом момента обладают 2J+1 состояний, различающихся проекцией Jz момента на ось z системы координат. Все эти состояния имеют одну и ту же энергию, то есть вырождены. Разумеется, разным значениям Jz соответствуют разные функции YJ,Jz , зависящие от угловых переменных и описывающие вращение молекулы. Радиальная функция отвечает условию нормировки (формула) (множитель R 2 возникздесь из-за перехода к сферическим координатам). Поскольку в
таком виде уравнение (7.4) для радиального движения выглядит несколько громоздко, его можно упростить, положив (фомула). Очевидно, условие нормировки для функции u(R) – это обычное условие (формула) =1, а уравнение для неё выглядит как уравнение Шредингера для одной частицы массы μ: (формула) (7.5)
Это уравнение мы будем использовать для описания колебательно-вращательных движений молекулы. Волновую функцию молекулы можно приближенно представить произведением нескольких функций:
а) электронной волновой функции Фn(r,R ), получаемой из электронного уравнения Шредингера (4.1),зависящей от радиус-векторов электронов rj
и их спиновых переменных, а также, как от параметров, от радиус-векторов всех ядер R,
б) волновой функции свободного движения центра масс молекулы — e ± i ( k , Rcm ) ,
в) вращательной части волновой функции YJ,Jz , зависящей лишь от угловых переменных, описывающих поворот молекулы как целого,
г) колебательной волновой функции un,J,v(R) , удовлетворяюшей уравнению (7.5).
При сделанных приближениях энергия молекулы – это сумма энергии свободного движения центра масс (поступательной энергии) и электронно-колебательно-вращательной энергии εn,J,v .
Электронно-колебательно-вращательную энергию молекулы можно получить, решая уравнение (7.5). На рисунках 2, 3 приведены результаты численного решения такойзадачи. (Следует отметить, что, решая ур.(7.5) мы определим не только электронно-колебательно-вращательную энергию, но и колебательную волновую функцию un,J,v(R), соответствующую этому энергетическому состоянию молекулы.) Для решения уравнения (7.5) необходимо знать функцию En(R) (электронную энергию или потенциал ядерного уравнения), являющуюся решением электронного уравнения Шредингера (4.1). Она может быть задана просто поточечно, однако очень часто потенциал En(R) аппроксимируют подходящей аналитической функцией. Вблизи точки минимума (R = Re) электронную энергию можно разложить в ряд, первые члены которого в квадратичном приближении будут иметь вид En(R) ≈ En(Re) + kn(R–Re) 2 /2 , где kne – вторая производная потенциала в точке Re : (формула).При J = 0 уравнение (7.5) с таким потенциалом нетрудно решить, так как это просто задача о
гармоническом осцилляторе: (формула) (8.1)
Значения энергии в такой задаче определяется как: (формула); где
(Формула)– классическая частота колебаний тела массы μ на пружине с силовой постоянной ke, v – номер колебательного уровня, En — электронная энергия данного электронного состояни при равновесном межъядерном расстоянии (Re). Волновые функции un,v(R–Re) выражаются как произведение полинома Эрмита и функции вида
exp(–β(R–Re) 2 ) с некоторым коэффициентом β, т.е. быстро спадают при удалении от точки R = Re. Если вернуться к первоначальной задаче с потенциалом En(R) , то с помощью сделанной оценки в гармоническом приближении можно методами теории возмущений вычислить значение энергии колебательного уровня с номером v более точно. При этом оказывается, что поправка к энергии оценивается рядом по степеням величины (v+1/2). В итоге получается ряд, обозначения и выбор знаков коэффициентов (колебательных постоянных) которого – спектроскопическая традиция: (формула) (8.2)
Величина ћωexe(v+1/2) 2 называется поправкой на ангармоничность, а коэффициент ωe xe – коэффициентом ангармоничности. Отметим, чтосогласно уравнению. (8.2) с ростом колебательного квантового числа vрасстояние между соседними уровнями энергии становится все меньше и меньше, тогда как в простом гармоническом приближении расстояние между колебательными уровнями остается величиной постоянной. Для аппроксимации функции En(R) часто используют потенциала Морзе:(формула). Точное решение ур.(7.5) с таким потенциалом соответствует выражению (8.2), если оборвать ряд на квадратичном по (v+1/2) слагаемом: (формула) (8.3)
Тогда можно найти и явные выражения для гармонической частоты ωe и коэффициента ангармоничности ωexe через параметры потенциала α и D: (формулы). В этом случае расстояние между колебательными уровнями энергии линейно зависит от v: εnv+1 – εnv = ћωe – 2ћωexe(v+1/2) . По выполнению такого линейного соотношения часто судят о применимости модели Морзе. Отметим, что число колебательных состояний для потенциала Морзе конечно ( в отличие от гармонического потенциала) – максимально возможное значение v можно найти из условия εnv+1 – εnv ≥ 0 , т.е. v≤ωe/(2ωexe)–1/2 .
Поведение радиальных функций un,0,v(R) колебательных движений ядер (при J = 0) можно понять из рисунка 2. Как видно из рисунка, при малых значениях колебательного квантового числа v волновые функции очень похожи на волновые функции гармонического осциллятора. Для R, отвечающих области, в которой двигалась бы классическая частица, т.е. между точками, в которых энергия частицы равна потенциалу (их называют «точками поворота»), функции осциллируют. В классически запрещенных областях ( где потенциал больше энергии) функции быстро спадают. Важно отметить, что даже при относительно небольших v колебательные волновые функции заметно отличны от нуля возле точек поворота. Это можно объяснить тем, что (по классическим представлениям) наиболее велика вероятность найти частицу в тех областях, где скорость её мала, то есть именно в окрестностях точек поворота. Описанное явление лучше видно на рисунке 3, изображающем распределение ядерной плотности в той же системе.
( 2 жопных не копирующихся рисунка)
Заметив, что волновые функции гармонического осциллятора локализованы возле равновесного расстояния, мы можем применить теорию возмущений и для учета энергии вращения. Применение теории возмущений даст поправки к энергии в виде ряда по степеням J(J+1). Например, в первом порядке теории возмущений надо просто рассмотреть среднее значение оператора (формула) на функциях unv(R–Re) гармонического осциллятора. Разложив оцениваемый потенциал в ряд по степеням (R–Re), находим, что при некоторых коэффициентах с 2 , с3,. поправка к энергии имеет вид:
( формула) где Bv , Dv , Hv … являются рядами по степеням (v+1/2).
Выписанное выражение для энергии позволяет, как и в классической модели
молекулы, представить внутреннюю энергию как сумму электронной (E е n ), колебательной и вращательной энергии: E = Ee + Evib +Erot . Состояние молекулы задается указанием электронного состояния (n; обычно указывается символ электронного состояния, например, 2 П), колебательным (v) и вращательным (J) квантовыми числами. В самом грубом приближении (жесткий ротатор) можно пренебречь зависимостью Bv от v и вообще не рассматривать остальные вклады во вращательную энергию.
Понятие «электронная конфигурация». Метод многоконфигурационного самосогласованного поля (МК ССП). Метод конфигурационного взаимодействия (КВ). Одноконфигурационное приближение: метод Хартри-Фока. Понятие «электронная корреляция». Ферми-корреляция и кулоновская корреляция.
Электронная конфигурация — формула расположения электронов по различным электронным оболочкам атома химического элемента или молекулы.
Метод многоконфигурационного взаимодействия (Multi-Configurational Self-Consistent Field – MCSCF) можно рассматривать как метод КВ, в котором оптимизируются не только коэффициенты перед детерминантами, но и коэффициенты разложения МО по АО.
Метод конфигурационного взаимодействия основан на вариационном принципе, аналогично методу Хартри – Фока. Пробная функция записывается в виде линейной комбинации детерминантов, и коэффициенты определяются из условия минимума энергии. Детерминанты классифицируют на однократно (s), дважды (d), трижды (t) и т.д. возбужденные, и функция конфигурационного взаимодействия приобретает следующий вид:
Применяя вариационный принцип, получаем набор секулярных уравнений:
(H — EI)a = 0; (3.5.3)
Здесь H– матрица конфигурационного взаимодействия (КВ),
I – единичная матрица.
Матричный элемент матрицы КВ вычисляется из детерминантов: 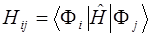
Для вычисления элементов матрицы КВ необходимы одно- (3.5.5) и двухэлектронные (3.5.6) интегралы между МО. Они могут быть выражены через соответствующие интегралы атомных орбиталей (АО) и коэффициенты МО:
Эти интегралы необходимы для всех методов, учитывающих электронную корреляцию. Двухэлектронные интегралы атомных орбиталей 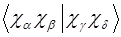
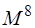
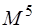
При численной реализации метода КВ сокращают число возбуждённых детерминантов. Включать только однократно возбуждённые детерминанты бессмысленно, так как все матричные элементы между ними и детерминантом Хартри-Фока равны нулю. Только дважды возбуждённые детерминанты дают отличные от нуля матричные элементы. Поэтому самым грубым приближением является включение в расчёт только двукратно возбуждённых детерминантов – модель CID (Configurational Interaction with Doubles). Включение однократно возбуждённых детерминантов даёт модель CISD (CI with Singles and Doubles). Хотя однократно возбуждённые детерминанты и дают нулевые матричные элементы с детерминантом Хартри-Фока, но они дают отличные от нуля матричные элементы с двукратно возбуждёнными детерминантами. Для больших базисов время счёта методом CISD пропорционально 6-й степени размера базиса ( 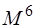
Следующая ступень улучшения – включение трижды возбуждённых детерминантов – метод CISDT (время счёта пропорционально 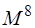
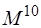
Метод Хартри – Фока даёт правильное решение на 99%, и логично его использовать за основу для дальнейшего улучшения. В общем мультидетерминантную функцию можно записать в следующем виде:
Здесь коэффициент а0 обычно близок к единице; 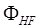
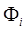
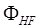
Недостатком метода Хартри – Фока является представление о движении электрона в усредненном поле всех остальных электронов. Но движение электронов является взаимозависимым – электроны стремятся расположиться как можно всегда дает завышенное значение общей энергии. Разность между энергией, вычисленной методом Хартри – Фока, и минимальной энергией, которую можно рассчитать в данном базисе, называется энергией электронной корреляции. дальше друг от друга вкаждый момент времени. В результате электроны в среднем располагаются несколько дальше друг от друга в сравнении с моделью усредненного поля Хартри, что снижает энергию их взаимодействия. Поэтому метод Хартри – Фока. Электронная корреляция – эффект, обусловленный мгновенным кулоновским отталкиванием между электронами (стремлением электронов «избежать друг друга»). Его учет приводит к более низкому значению полной энергии системы. Не учитывается в методе Хартри-Фока. Изменение энергии, вызванное этими мгновенными кулоновскими взаимодействиями, называется энергией корреляции: Eкорреляц. = Eточн. — EХФ (0) , например функции водородоподобного атома. С исходным набором функций рассчитывают óстовный и кулоновский интегралы, а затем решаются уравнения для каждого значения i. Другими словами, решается задача на собственные значения и собственные вектора оператора Хартри, который приближённо считается равным оператору Гамильтона.
Найденные функции 1-го приближения Ψj (1) используются вновь для расчёта óстовного и кулоновского интегралов, и процедура повторяется – вычисляют функции Ψj (2) , Ψj (3) , … и соответствующие им энергии E (2) , E (3) , … . Повторение вычислений проводят до тех пор, пока для функций Ψj ( n ) и Ψj ( n +1) величины эффективных потенциалов (и соответствующие им энергии E ( n ) и E ( n +1) ) не будут совпадать с заданной точностью. Это требование обусловливает название метода самосогласованного поля (ССП, SCF – Self-Consistent Field).
Недостатком метода Хартри является неправильный вид общей волновой функции, представленной в виде произведения одноэлектронных функций (3.2.6). Электроны являются фермионами – частицами с полуцелым спином, и, в соответствии с принципом Паули, система из нескольких электронов должна описываться антисимметричной волновой функцией. Это значит, что при перестановке двух электронов функция должна менять знак на противоположный: 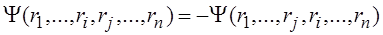
Поэтому Владимир Александрович Фок* усовершенствовал метод Хартри, предложив антисимметричную общую волновую функцию в виде определителя Слэйтера, составленного из ортонормированных ( 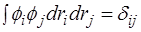
💡 Видео
Лучшая модель атома? [Минутка физики]Скачать
![Лучшая модель атома? [Минутка физики]](https://i.ytimg.com/vi/eybcxXiYJfc/0.jpg)
Хренова М.Г. - Квантовая химия - 2. Атом водородаСкачать

Структура материи 6: уравнение Шрёдингера. Зачем нужна квантовая механика – Виталий Бейлин | НаучпопСкачать

Квантовые числа (видео 14) | Квантовая физика | ФизикаСкачать

Атомная физика. Лекция 14. Атом водорода. Гамильтониан и решение уравнения Шредингера.Скачать

Квантовая механика 41 - Уравнение Шредингера. Гамильтониан.Скачать

Квантовые числа. 1 часть. 10 класс.Скачать

Теория Бора. Гипотеза де Бройля. Принцип неопределенности. Уравнение Шрёдингера.Скачать

96. Уравнение ШредингераСкачать

Классические уравнения | уравнение Шрёдингера (координатное представление) | простейший выводСкачать

Уравнение ШрёдингераСкачать

Устройство атома от Томсона до ШрёдингераСкачать

Лекции 5-6. Уравнение Шредингера и его приближенные решения. Межатомные.Скачать

Шрёдингер и его уравнение — Дэвид Клэри / ПостНаукаСкачать

Корректный вывод уравнения Шрёдингера и его физический смысл: Липовка А.А. - Глобальная волнаСкачать

Лекция №4 "Волновая функция. Уравнение Шредингера" (Гавриков А.В.)Скачать