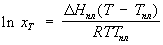Уравнение Шредера

Раствор в отличие от чистой жидкости не отвердевает целиком при постоянной температуре; при некоторой температуре, называемой температурой начала кристаллизации, начинают выделяться кристаллы растворителя и по мере кристаллизации температура раствора понижается (поэтому под температурой замерзания раствора всегда понимают именно температуру начала кристаллизации). Рассмотрим случай, когда при охлаждении идеального совершенного раствора кристаллизуется только один компонент — тот компонент, которого больше, т. е. растворитель.

Уравнения, характеризующие это равновесие, имеют вид

Уравнение (5.13) называется уравнением Шредера, оно применимо для идеальных совершенных растворов. Данное уравнение описывает равновесие «жидкость — кристаллы растворителя». Температуру, наблюдаемую при этом, называют температурой кристаллизации, соответственно, температурой кристаллизации чистого растворителя и температурой кристаллизации раствора.

Интегральная форма уравнения Шредера для идеального раствора

Видео:09 Фаз диагр двухкомп сист 3 растворыСкачать

для нсидеального раствора

Закон понижения температуры кристаллизации

где называется криоскопической постоянной.

Содержание

Диаграмма плавкости 2-х компонентных систем. Диаграммы плавкости систем с конгруэнтно и инконгруэнтно плавящимися соединениями
Страницы работы
Содержание работы
Шредера уравнение
🔥 Видео

Диаграмма плавкости 2-х компонентных систем. Диаграммы плавкости систем с конгруэнтно и инконгруэнтно плавящимися соединениями

Страницы работы

Содержание работы

19.Диаграмма плавкости 2-х компонентных систем.

Диаграмма плавкости выражает зависимость температур плавления смесей от их состава. Частным случаем диаграмм плавкости являются диаграммы растворимости, представляющие зависимость растворимости твердых веществ в жидкости от температуры.

Состояние двухкомпонентной сист. определяется 3 параметрами (температура, давление и концентрация одного из компонентов)

Видео:Лекция «Диаграмма состояния двухкомпонентных сплавов»Скачать

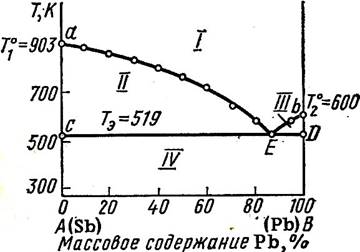
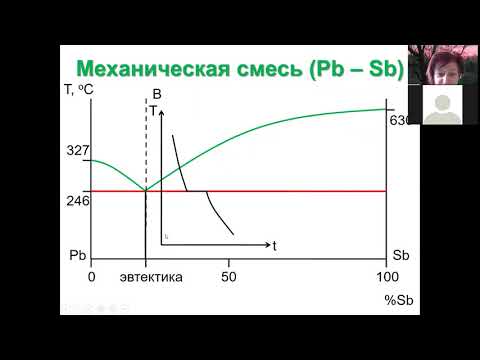
Системы без образования химических соединений

I — жидкий расплав (С=2-1+1=2);

II — жидкий расплав и кристаллы комп-та А (С=

III — жидкий расплав и кристалы

Компонента В (С=2-2+1=1);

Видео:09 Фаз диагр двухкомп сист 1 принципы и мех смесьСкачать

IV — кристалы А и В (С=2-2+1=1);

Линия aEb называется линией ликвидуса – составы жидких расплавов, при охлаждении которых до данной температуры начинается кристаллизация из расплава чистого компонента А или В.

Линия СED линией солидуса, ниже нее жидкость не может существовать.

Точка E называется эвтектической точкой – она соответствует расплаву, который одновременно находится в равновесии с кристаллам компонента А и В. Расплав этот называется эвтектическим, а смесь выпадающих кристаллов при T_э эвтектикой. Эвтектика кристаллизуется при постоянной температуре – система условно инвариантна, т.к. при изменении давления меняется и температура плавления и состав эвтектики. При кристаллизации эвтектики состав жидкого расплава отличается от состава каждой из равновесных с ним твердых фаз.

20(1).Диаграммы плавкости систем с конгруэнтно и инконгруэнтно плавящимися соединениями.

Видео:09 Фазовые диаграммы 2 правило фазСкачать

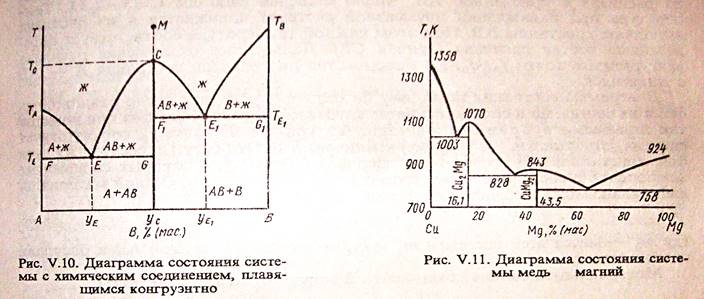
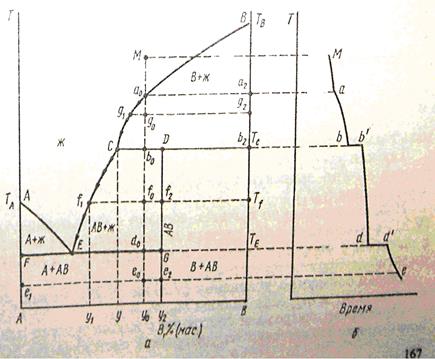
Если компоненты А и В могут образовывать тв. хим. соединение АВ, плавящееся без разложения, т.е. конгруэнтно, то на диаграмме состояния кривая ликвидуса образует максимумы в точке С, когда состав кристаллической фазы совпадает с составом жид. фазы. По обе стороны от точки С нах-ся эвтектики Е и Е₁. Если состав системы находится между чистым компонентом А и химическим соединением АВ, то при эвтектической температуре Т_Е, расплав состава у_Е сосуществует с кристаллами А и АВ. Если состав системы лежит между хим. соед. АВ и компонентом В, то при Т_Е1 расплав состава у_Е1 сосуществует с кристаллами АВ и В. Т.о. рассмотренная диаграмма состояния – сочетание 2-х диаграмм состояния с эвтектикой А – АВ и АВ – В.

Процесс охлаждения расплава, заданного точкой М. При этом составе число независимых комп-ов = 1, т.к. система может быть образована только из одного хим. соед. АВ. При Т_С из расплава выпадают кристаллы АВ (Ф=2) и число степ. своб. С=1-2+1=0, т.е. система безвариантна и кристаллизуется при постоянной температуре.

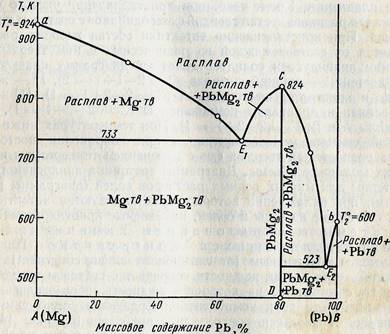
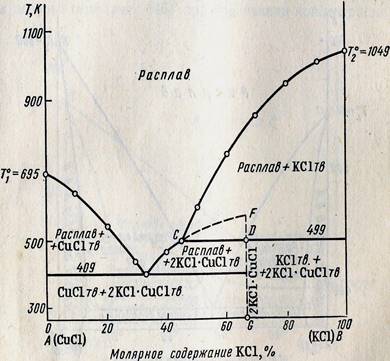
Хим. соед-ия при достижении определенной температуры начинают плавиться, распадаясь на кристаллическую и жидкую фазы, составы которых не совпадают. Если компоненты А и В образуют твердое химическое соединение АВ, плавящееся с разложением, т.е. инконгруэнтно, то АВ устойчиво только ниже Т_С. При малейшем ↑ t-ры это твердое соединение распадается и образуются 2 фазы: кристаллы В и расплав состава у (точка С).При охлаждении расплава состава М в точке а₀ начнется выделение кристаллов компонента В. В интервале температур от а₀ до b₀ сист. явл. 2-х фазной и одновариантной: С=2-2+1=1. В точке b₀при Т_С начинается и продолжается кристаллизация соединение АВ, состав которого соответствует у₂ (т. D). В равновесии 3 фазы: расплав, кристаллы АВ и В. С=2-3+1=0 – постоянство Т_С, состава раствора у (т. С) и состава хим. соединения у₂ (т.D).

Чтобы состав расплава не изменялся, одновременно с кристаллизацией АВ ранее выпавшие кристаллы В должны раств-ся, поддерживая постоянным соединение компонента В в расплаве. Т. С наз-ся перитектикой (переходной), Т_С — перитектическая температура. В этой точке находятся в равновесии расплав и 2 тверд. фазы, но в отличается от эвтектики, (где одновременно выпадают 2 тв. фазы) одна тв. фаза выпадает, а другая растворяется. На кривой охлаждения наблюдается горизонтальный участок (bb’).

Процесс охлаждения в точке b₀ заканчивается растворением всех ранее выпавших кристаллов В. Остается 2-х фазная система, состоящая из расплава и кристаллов АВ. При этом каждой температуре соответствует определенный состав расплава (СЕ). Дальнейшее охлаждение описывается диаграммой состояния А-АВ с эвтектикой.

21. Дифферинциальный термический анализ (ДТА)

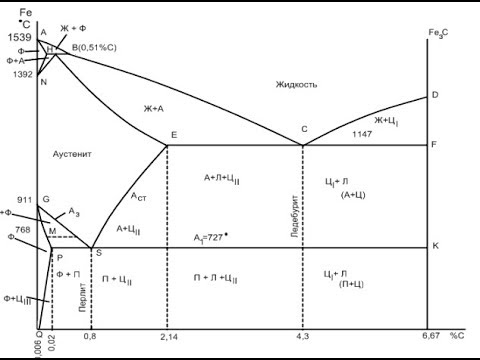
Видео:Диаграмма состояния сплавов системы «железо-углерод»Скачать

ДТА – это нахождение зависимости между температурой плавления вещества и его свойствами.Метод позволяет изучать фазовый состав Ме систем, природных минералов, устанавливать тем-ые границы сущ-ия многих соединений (соли, полимеры), определять теплоты фазовых превращений, теплопров-ть, теплоемкость.

Метод основан на автоматической записи дифференциальной термопарой термограмм – кривых ∆Т – Т, где ∆Т – разность температур м/у исследуемым веществом и эталоном, нагреваемых или охлаждаемых в одинаковых условиях; Т – температура образца или время нагревания/охлаждения. Эталон – в-во, не имеющее фазовых превращений в исследуемом интервале температур.

Вид термограммы исследуемого в-ва зависит от свойств самого в-ва (состав, структура, теплопроводность, теплоемкость, дисперсность и др.) и от условий снятия термограммы (скорость нагревания, величина навески, плотность набития в-ва в тигле, положения спая в образце и в эталоне, свойства эталона, чувствительность в цепи дифференциальной термопары).

Шредера уравнение

Шр е дера уравн е ние, математическое соотношение, выражающее связь между растворимостью кристаллического тела x_t при температуре Т (в К), его теплотой плавления D Н_пл (в кал/моль) и температурой плавления Т_пл:

Видео:ДИАГРАММА СОСТОЯНИЯ ЖЕЛЕЗО-ЦЕМЕНТИТ, железо-углерод, Fe+Fe3CСкачать

где R — газовая постоянная; D Н_пл принимается постоянной в интервале Т_пл — Т. Строгое применение Шредера уравнения ограничено идеальными растворами. Построив по Шредера уравнению кривые температурной зависимости растворимости для твёрдой фазы каждого из компонентов двойной системы, можно найти эвтектическую точку (см. Эвтектика) и получить растворимости диаграмму.

Шредера уравнение выведено в 1890 И. Ф. Шредером. Оно известно также под названием «логарифмики Шредера» и уравнения Шредера — Ле Шателье (А. Ле Шателье ранее получил зависимость растворимости от температуры в дифференциальной форме, на основании которой в 1894 вывел уравнение, аналогичное Шредера уравнению).

Лит.: Кипнис А. Я., Развитие химической термодинамики в России, М.—Л., 1964. См. также лит. при ст. Растворы.