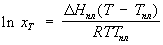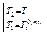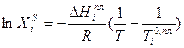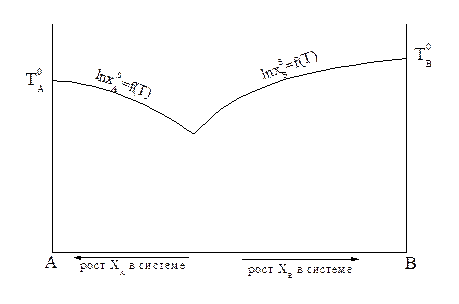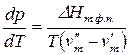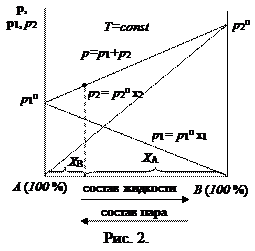Шредера уравнение

Шр е дера уравн е ние, математическое соотношение, выражающее связь между растворимостью кристаллического тела x_t при температуре Т (в К), его теплотой плавления D Н_пл (в кал/моль) и температурой плавления Т_пл:

где R — газовая постоянная; D Н_пл принимается постоянной в интервале Т_пл — Т. Строгое применение Шредера уравнения ограничено идеальными растворами. Построив по Шредера уравнению кривые температурной зависимости растворимости для твёрдой фазы каждого из компонентов двойной системы, можно найти эвтектическую точку (см. Эвтектика) и получить растворимости диаграмму.

Шредера уравнение выведено в 1890 И. Ф. Шредером. Оно известно также под названием «логарифмики Шредера» и уравнения Шредера — Ле Шателье (А. Ле Шателье ранее получил зависимость растворимости от температуры в дифференциальной форме, на основании которой в 1894 вывел уравнение, аналогичное Шредера уравнению).

Лит.: Кипнис А. Я., Развитие химической термодинамики в России, М.—Л., 1964. См. также лит. при ст. Растворы.

Видео:Коробов М. В. - Физическая химия. Часть 1 - Энергия Гиббса образования раствора. Уравнение ШредераСкачать

Равновесие раствор – кристаллический компонент

Если два компонента А и В смешать, расплавить до получения однородного раствора, а затем начать охлаждать, то при некоторой температуре из раствора начнут образовываться кристаллы, так как растворимость веществ с понижением температуры, как правило, умень­шается. В зависимости от состава исходного раствора при понижении температуры он становится насыщенным по отношению либо к компоненту А, либо В, что приводит к кристаллизации соответственно А или В. В зависимости от состава раствора температура начала кристаллизации будет также различной. Иначе говоря, состав раствора, насыщенного каким-либо компонентом, т.е. растворимость этого компонента, зависит от температуры.

Уравнением, описывающим зависимость растворимости кристалличе­ских веществ в жидкостях от температуры, является уравнение Шредера:

, (2.7)

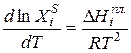
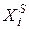
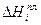
где — молярная доля i-гo компонента в растворе, насыщенном по отношению к этому компоненту; — теплота плавления этого компонента.

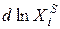
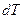
Уравнение Шредера справедливо только для идеальных растворов. Из анализа уравнения (2.7) следует, что растворимость твердых веществ в жидкостях растет с ростом температуры. Действительно, правая часть уравнения для идеальных растворов всегда больше нуля, следовательно, производная / > 0, т.е. X_i растёт с ростом температуры.

Интегрируя уравнение (2.7) для бинарной системы в пределах от Х₁=1 (чистый компонент) до Х₂ = X s (насыщенный раствор при любой температуре), получим уравнение Шредера в интегральной форме:

—

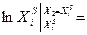
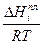
Пользуясь этим уравнением, можно найти растворимость i-гo компо­нента, выраженную в молярных долях Xi при любой температуре. Если раствор идеален и рассматривается во всём интервале концентраций от Х_А = 1 до Х_в = I, необходимо иметь в виду, что при одних составах раствор оказывается насыщенным компонентом А (здесь надо говорить о растворимости компонента А в В), при других — компонентом В (здесь уже идет речь о растворимости В в А). В первом случае применимо уравнение Шредера для компонента А; во втором – для компонента В:

(2.8)

(2.9)

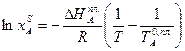
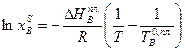
Очевидно, должен быть и такой раствор, который является насыщенным сразу обоими веществами, для него 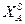= 1 — . Координаты такой системы X s и Т находятся совместным решением уравнений 2.8 и 2.9 или графическим пересечением кривых, описываемых уравнениями 2.8 и 2.9. Кривые изменения растворимости компонентов А и В с температурой можно изобразить на одной диаграмме (рисунок 2.4).

Рисунок 2.4 — Кривые зависимости растворимости компонентов А и В от температуры

Кривые охлаждения

Расчёт диаграмм растворимости (с равным правом их можно назвать диаграммами плавкости) возможен лишь для идеальных систем. Для реальных систем приходится экспериментально определять температуру, при которой раствор данной концентрации становится насыщенным. Это производится путем снятия так называемых кривых охлаждения для систем нескольких составов (метод называется термическим анализом), в координатах (температура; время).

При охлаждении однокомпонентной жидкости сначала происходит равномерное понижение температуры во времени. Появление кристаллов сопровождается выделением тепла, которое компенсирует теплоотвод, и дальнейшего понижения температуры в системе не происходит до полной кристаллизации жидкости, после чего температура снова понижается (рисунок 2.5 а).

Для двухкомпонентной системы наблюдается иной тип кривой охлаждения (рисунок 2.5 б). Сначала жидкая система охлаждается равномерно с определенной скоростью 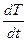. Затем при какой-то температуре Т раствор становится насыщенным по отношению к какому-либо одному из компонентов, и этот компонент образует первые кристаллы. При данной температуре устанавливается равновесие между раствором и кристаллами. Дальнейшая кристаллизация этого компонента возможна лишь при понижении температуры. Таким образом, кристаллизация одного компонента из раствора происходит не при одной температуре, как в случае чистого вещества, а в некотором интервале температур. Поскольку кристаллизация вещества происходит небольшими порциями, то выделяющейся теплоты кристаллизации недостаточно для температурной остановки: происходит лишь уменьшение скорости охлаждения, кривая охлаждения становится более пологой.

По мере выделения одного из компонентов в третью фазу, происходит накапливание второго компонента в растворе. Наконец при некоторой температуре раствор становится насыщенным по отношению и ко второму компоненту, т.е. начинается кристаллизация обоих компонентов одновременно.

Смесь кристаллов, образующихся при совместной кристаллизации двух компонентов, называется эвтектикой.

Эвтектика имеет определенный состав, наименьшую и всегда постоянную (эвтектическую) температуру кристаллизации (плавления) при данном давлении. Если взять расплав, соответствующий составу эвтектики, то кривая охлаждения будет иметь вид (рисунок 2.5 в). В сплавах, отличающихся по составу от эвтектического, всегда первым будет кристаллизоваться компонент, находящийся в избытке по сравнению с составом эвтектики, а затем, когда избыток выкристаллизуется, а состав станет равным эвтектическому, будет кристаллизоваться эвтектика. Таким образом, у сплавов с различным составом начинается кристаллизация при различных температурах, а заканчивается при одной и той же, эвтектической температуре. Анализируя кривые охлаждения, находят температуры начала кристаллизации расплавов и, нанеся эти точки на диаграмму Т – состав получают линию ликвидуса, а соединяя точки, отвечающие температуре конца затвердевания, вычерчивают линию солидуса. Так получают диаграмму плавкости.

Рисунок 2.5 – Типы кривых охлаждения:

а – для чистого вещества А;

б – для смеси веществ А + В;

в – для эвтектической смеси;

г – кривая охлаждения в случае оразования метастабильного состояния (переохлажденного состояния);

д – для системы, где нет фазовых превращений

Видео:Как расставлять коэффициенты в уравнении реакции? Химия с нуля 7-8 класс | TutorOnlineСкачать

ВЛИЯНИЕ ДАВЛЕНИЯ НА КОНСТАНТУ ХИМИЧЕСКОГО

РАВНОВЕСИЯ (УРАВНЕНИЕ ПЛАНКА)

Для установления влияние давления на реакции, протекающие с участием газообразных веществ, воспользуемся константой равновесия, выраженной через равновесные мольные доли, K_х= f(T, p).

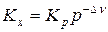
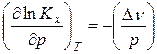
Выражение (9), записанное в виде , логарифмируют и полученное выражение с учетом того, что K_р не является функцией давления, дифференцируют по давлению при постоянной температуре

. (18)

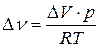
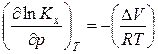
Считая газы, участвующие в реакции, идеальными, можно из уравнения Менделеева-Клапейрона выразить изменение числа моль газообразных веществ в реакции и подставить в уравнение (18). Тогда

. (19)

Уравнения (18) и (19) описывают влияние давления на химическое равновесие в идеальной газовой реакции и называют уравнением Планка. Проведем анализ данного уравнения:

1) если реакция протекает с увеличением объема (количества вещества), то при повышении давления 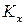уменьшается. Это означает, что для реакций типа
А + B = 3C с ростом давления равновесие смещается в сторону исходных веществ;

2) если реакция протекает с уменьшением объема (количества вещества), то при повышении давления 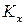увеличивается. Для реакций типа А + 2B = C с ростом давления равновесие смещается в сторону продуктов реакции;

3) если реакция протекает без изменения объема (количества вещества), то при повышении давления 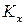не изменяется. Это означает, что для реакций типа
А + B = 2C с ростом давления равновесие не изменяется.

Влияние давления на химическое равновесие в растворе незначительно, так как объем раствора практически не изменяется.

3. растворы и гетерогенные равновесия

3.1. Основные понятия и определения

Термодинамическую систему однородную по физическому строению и химическим свойствам во всех точках, называют гомогенной.

Термодинамическую систему, состоящую из различных по физическим или химическим свойствам частей, отделенных друг от друга поверхностями раздела, называют гетерогенной.

Любая гетерогенная система состоит из нескольких фаз. Фаза – это гомогенная часть гетерогенной системы, ограниченная поверхностью раздела, при переходе через которую свойства системы меняются скачкообразно. Системы делятся на одно–, двух–, трехфазные и т.д.

Каждая система состоит из одного или нескольких веществ, называемых компонентами. Вещества, образующие термодинамическую систему, могут находиться в различных агрегатных состояниях: газообразном, жидком, твердом. Числом независимых компонентов называют наименьшее число индивидуальных компонентов, необходимое для образования данной системы, которое равно общему числу индивидуальных веществ, входящих в данную систему, за вычетом числа уравнений, связывающих равновесные концентрации этих веществ. По числу компонентов различают одно–, двух–, трех– и т.д. компонентные системы.

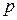
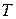
Любая система характеризуется внешними ( , , и т.д.) и внутренними (концентрационными) параметрами состояния или концентрациями, которые определяют равновесный состав фаз.

Число концентрационных параметров данной фазы равно числу независимых компонентов, входящих в ее состав фазы, за вычетом единицы (так как, например, если система состоит их двух компонентов, то концентрацию второго компонента можно определить, зная концентрацию первого).

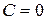
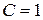
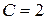
Число независимых термодинамических параметров состояния данной системы, произвольное изменение которых в определенных пределах не вызывает исчезновения одних и образование других фаз называют числом термодинамических степеней свободы или вариантностью системы. По числу термодинамических степеней свободы системы разделяются на инвариантные ( ), моновариантные ( ), дивариантные ( ) и т.д.

3.2. Термодинамика растворов

3.2.1. ОСНОВНЫЕ ПОНЯТИЯ

Раствором называют гомогенную однофазную систему, состоящую минимум из двух независимых компонентов, в каждом элементарном объеме которого одинаковые физические, химические и термодинамические свойства. В жидких растворах обычно различают растворитель – это вещество, которое имеется в растворе в избытке, и растворенные вещества, хотя все компоненты раствора термодинамически равноценны. Компоненты, находящиеся в растворе в меньшем количестве называют растворенными веществами.

Растворы подразделяют на идеальные и реальные. Идеальным называют раствор, все компоненты которого характеризуются одинаковой формой и размером молекул и одинаковой энергией межмолекулярных взаимодействий. Идеальные растворы встречаются довольно редко. Это гомогенные смеси близких по физико-химическим свойствам веществ (смеси оптических изомеров, соседних членов одного и того же гомологического ряда). Моделью идеального газового раствора является смесь идеальных газов.

Большинство растворов являются реальными, их компоненты отличаются либо по форме, либо по размерам, либо по энергии межмолекулярных взаимодействий.

Все свойства растворов подразделяют на экстенсивные и интенсивные.

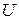
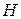
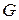
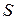
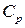
Экстенсивные свойства, зависят как от общей массы раствора, так и от его состава, например , , , , . Эти свойства относятся ко всему раствору, как единому целому, а не к отдельным его компонентам.

Интенсивные свойства, зависят только от состава раствора и не зависят от его общей массы, например, давление насыщенного пара.

Для характеристики растворов используют средние мольные и парциальные мольные свойства.

Среднее мольное свойство – экстенсивное свойство 1 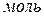раствора.

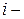
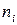
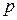
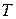
Парциальное мольное свойство го компонента – это частная производная от экстенсивного свойства раствора по числу моль этого компонента ( ) при постоянном числе моль всех остальных компонентов и внешних параметрах ( , ).

Среди парциальных молярных величин наибольшее значение имеет парциальная мольная энергия Гиббса, которая называется химическим потенциалом .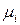

Химический потенциал является интенсивным свойством раствора.

3.2.2. УСЛОВИЕ РАВНОВЕСИЯ В ГОМОГЕННЫХ РАСТВОРАХ

Равновесие в гомогенном идеальном растворе выражает уравнение Гиббса–Дюгема:

, (1)

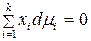
которое для двухкомпонентного раствора записывается в виде

.

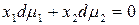
Равновесие в гомогенном реальном растворе выражает уравнение Дюгема–Маргулеса:

. (2)

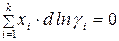
Для двухкомпонентного раствора условие равновесия записывается:

.

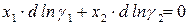
3.3. гетерогенные равновесия

3.3.1. равновесие в гетерогенной системе. Правило фаз гиббса

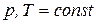
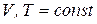
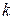
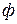
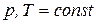
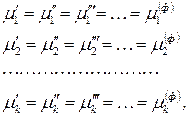
Условием термодинамического равновесия в гетерогенной системе является равенство химических потенциалов каждого компонента во всех фазах при или :

Для –компонентной и –фазной системы при условие термодинамического равновесия (теорема Гиббса) выражается системой уравнений

(3)

где индекс 1, 2,…, 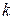– номер компонента;

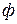
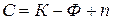
¢,²,¢¢¢,…, – номер фазы.

В равновесной системе связь между числом фаз, числом компонентов и числом термодинамических степеней свободы выражает основной закон фазового равновесия или правило фаз Гиббса:

, (4)

где 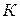– число независимых компонентов;

n – число внешних параметров, влияющих на состояние равновесия.

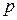
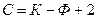
Если на систему влияют два внешних параметра ( и ), то правило фаз Гиббса записывается

.

Применим правило фаз Гиббса к анализу диаграммы состояния однокомпонентной системы, например, воды. В области средних давлений и средних температур вода может находиться в жидком, твердом (лед) и газообразном (пар) состояниях.

На рис. 1:

плоскость ОВС отвечает состоянию воды;

АОС – состоянию пара;

АОВ – состоянию льда;

О – тройная точка;

ОВ – кривая плавления;

ОС – кривая испарения;

ОА – кривая возгонки;

ОD – кривая давления насыщенного пара над переохлажденной водой.

Определим число степеней свободы в точках 1, 2 и тройной точке О.

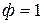
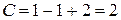
В точке 1 вода находится в жидком состоянии, следовательно, число фаз , тогда

.

Число степеней свободы равно двум или система дивариантна. Это означает, что можно произвольно в определенных пределах изменять два параметра: давление и температуру, при этом число и вид фаз системы не изменится.

Точка 2 находится на кривой испарения, следовательно, в равновесии находятся две фазы: жидкость и пар. Тогда

.

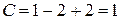
Система моновариантна, следовательно, возможно изменение одного параметра: температуры или давления, при котором число и вид фаз системы не изменится.

В тройной точке О в равновесии находятся три фазы: вода, лед и пар, тогда

.

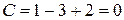
Система нонвариантна. Это означает, что три фазы могут находиться в равновесии только при определенных условиях.

3.3.2. Уравнение состояния однокомпонентной двухфазной системы

Состояние однокомпонентной двухфазной системы характеризуется уравнением Клаузиуса–Клапейрона:

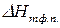
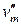
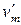
где – мольная теплота фазового перехода;

, – мольный объем вещества в фазе ² и ¢ соответственно.

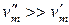
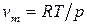
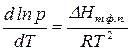
Для процесса возгонки и испарения можно допустить, что . При условии, что паровую фазу можно считать идеальной, в соответствии с уравнением Менделеева–Клапейрона , тогда уравнение Клаузиуса–Клапейрона запишется:

. (5)

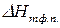
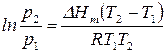
Разделив переменные и проинтегрировав в определенных пределах в узком интервале температур, считая постоянной величиной, получим

.

На основе полученного уравнения можно рассчитать:

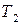
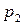
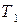
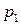
1) температуру кипения вещества под давлением , если известна температура кипения этого вещества под давлением и величина средней мольной теплоты испарения;

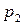
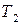
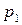
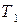
2) давление насыщенного пара индивидуального вещества при температуре , если известно давление насыщенного пара при температуре и средняя мольная теплота испарения;

3) среднюю мольную теплоту испарения или возгонки вещества, если известны значения давления насыщенного пара вещества при двух температурах.

3.3.3. фазовое равновесие жидкость-пар

Пусть существуют в состоянии равновесия жидкость и выделяющийся из нее пар. Если жидкий раствор является идеальным, то во всем интервале концентраций растворитель и растворенное вещество подчиняются закону Рауля:

, (6)

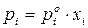
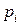
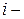
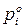
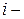
где – давление насыщенного пара го компонента над раствором;

– давление насыщенного пара над индивидуальным м компонентом при температуре раствора.

Для двухкомпонентного раствора можно записать:

; .

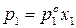
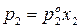
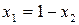
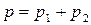
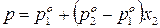
Так как , а общее давление над раствором складывается из парциальных давлений компонентов , то

.

Таким образом, зависимость давления насыщенного пара компонентов и общего давления пара от состава идеального раствора является линейной (диаграмма 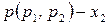на рис. 2).

На практике чаще приходится встречаться с неидеальными растворами, которые не подчиняются закону Рауля. Для описания зависимости давления насыщенного пара компонента от состава реального раствора в закон Рауля вводится коэффициент активности:

.

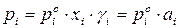
Для двухкомпонентного раствора общее давление смеси равно:

.

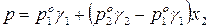
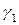
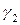
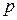
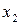
Поскольку коэффициенты активности и зависят от состава раствора, то зависимость от представляет собой кривую. Отклонения давления пара от линейной зависимости в сторону больших значений называют положительными, а в сторону меньших значений – отрицательными отклонениями от закона Рауля (рис. 3). Отклонения

зависят от относительной величины энергии взаимодействия молекул жидкой смеси.

Иногда отклонения бывают настолько велики, что на кривых давление (температура) – состав появляется ярко выраженный экстремум (минимум или максимум).

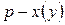
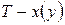
Точки на диаграммах и , которым отвечает максимум давления насыщенного пара (минимум температуры кипения) называют положительными (рис. 4а), а если минимум давления (максимум температуры кипения) – отрицательными азеотропами (рис. 4б).

Как видно из рис. 4, в точке азеотропа состав жидкой и паровой фаз одинаков. Бинарные смеси, которые содержат азеотроп, называют азеотропными.

Состав равновесного с жидким раствором пара определяется согласно закону Дальтона:

– для идеального раствора;

– для реального раствора.

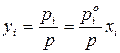
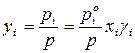
Из анализа последних уравнений видно, что рассчитать равновесный состав пара можно только для идеального раствора заданного состава. Для расчета равновесного состава паровой фазы реального раствора необходимо знать коэффициенты активности, численные значения которых определяют только экспериментальным путем.

Для представления данных по фазовому равновесию жидкость-пар кроме рассмотренных диаграмм применяют также диаграммы , , .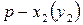

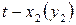
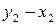
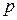
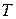
Для разделения жидких бинарных смесей используют методы перегонки и ректификации (многократной перегонки), которые основаны на различие составов жидкой и паровой фаз. Азеотропные смеси этими методами разделить невозможно. Для разделения азеотропных смесей необходимо создать условия, устраняющие азеотроп. Например, изменить значения внешних параметров ( , ) или добавить к бинарной смеси третий компонент, в присутствии которого азеотроп отсутствует.

Эбуллиоскопия

Эбуллиоскопия – явление повышения температуры кипения раствора нелетучего вещества по сравнению с температурой кипения чистого растворителя.

Основной закон эбуллиоскопии записывается:

, (7)

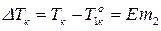
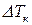
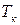
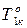
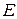
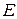
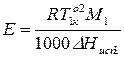
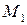
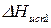
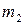
где – повышение температуры кипения; , – температура кипения раствора нелетучего вещества и чистого растворителя;

– эбуллиоскопическая константа (для воды = 0,52 (град·кг)/моль)

, (8)

– молекулярная масса растворителя; – теплота испарения растворителя; – моляльная концентрация растворенного вещества.

3.3.4. Фазовое равновесие твердое тело-жидкость. Уравнение шредера

Предположим, что в состоянии термодинамического равновесия существуют раствор твердого вещества в жидком растворителе и кристаллы данного твердого вещества. Равновесие в такой системе описывается уравнением Шредера:

,

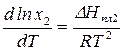
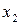
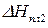
где – мольная доля растворенного вещества;

– теплота плавления твердого вещества.

После интегрирования получаем:

,

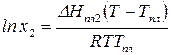
где 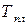– температура плавления чистого твердого вещества.

Полученное уравнение справедливо для растворов, близких по свойствам к идеальным, поэтому уравнение Шредера позволяет рассчитывать растворимость только малорастворимых веществ.

Криоскопия

Криоскопия – явление понижения температуры замерзания раствора нелетучего вещества по сравнению с температурой замерзания чистого растворителя.

Основной закон криоскопии записывается:

, (9)

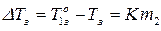
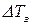
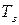
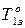
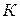
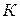
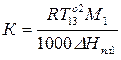
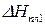
где – понижение температуры замерзания;

– температура замерзания раствора нелетучего вещества;

– температура замерзания чистого растворителя;

– криоскопическая константа (для воды = 1,86 (град·кг)/моль)

, (10)

– теплота плавления растворителя.

Методы криоскопии и эбуллиоскопии часто применяют для расчета молекулярной массы растворенного вещества.

3.3.5. фазовое равновесие жидкость-жидкость

Пусть в сосуде находятся две жидкости, практически не смешивающиеся друг с другом, например, вода и хлороформ. Если ввести в эту систему небольшое количество третьего вещества, например йода, то оно вполне определенным образом распределится между двумя жидкими фазами. В соответствии с законом распределения Нернста: при установлении равновесия отношение концентраций распределяющегося вещества в двух несмешивающихся жидкостях есть величина постоянная при постоянной температуре:

, (11)

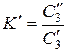
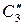
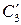
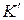
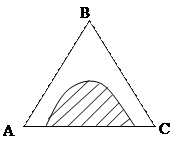
где , – равновесные концентрации распределяющегося вещества в двух соприкасающихся фазах;

– коэффициент распроеделения.

Закон распределения Нернста лежит в основе процесса жидкостной экстракции – извлечения вещества из раствора при помощи другого растворителя, практически не смешивающегося с первым. Экстракция широко применяется в промышленности.

Состояние трехкомпонентных систем с ограниченной растворимостью принято изображать с помощью треугольных диаграмм. На рисунке приведена диаграмма растворимости в трехкомпонентной системе с одной парой ограниченно смешивающихся компонентов и . Вершины треугольника соответствуют содержанию 100 % компонентов , и . Любая точка внутри треугольника выражает состав трехкомпонентной системы. Заштрихованная плоскость соответствует области гетерогенного (двухфазного) состояния системы. Линия, ограничивающая гетерогенную область, называется изотермой взаимной растворимости.

4. химическая кинетика

Химическая кинетика – наука о скорости протекания химической реакции.

Скорость химической реакции – изменение концентрации одного из реагирующих веществ в единицу времени.

Поскольку в реакциях вещества участвуют в стехиометрических соотношениях, за скорость реакции может быть принята производная от концентрации любого из реагирующих веществ по времени:

, (1)

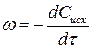
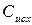
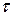
где – концентрация исходных веществ;

– время.

Концентрация исходных веществ убывает, поэтому перед производной стоит знак минус.

Если в качестве одного из реагирующих веществ выбран продукт реакции, то

. (2)

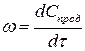
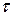
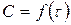
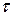
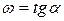
Скорость реакции в момент времени равна тангенсу угла наклона касательной, проведенной к кривой зависимости в точке, соответствующей времени :

.

4.1. основной закон химической кинетики.

📺 Видео

Урок 455. Уравнение ШрёдингераСкачать

Химические уравнения // Как Составлять Уравнения Реакций // Химия 9 классСкачать

Как Решать Задачи по Химии // Задачи с Уравнением Химической Реакции // Подготовка к ЕГЭ по ХимииСкачать

Как выучить Химию с нуля за 10 минут? Принцип Ле-ШательеСкачать

Как Решать Задачи по Химии // Задачи с Уравнением Химической Реакции // Химия ПростоСкачать

Составление уравнений химических реакций. 1 часть. 8 класс.Скачать

Теории кислот, оснований и растворов. Теория Аррениуса-Оствальда. 11 класс.Скачать

Расчеты по уравнениям химических реакций. 1 часть. 8 класс.Скачать

8 класс. Составление уравнений химических реакций.Скачать

Окислительно-восстановительные реакции в кислой среде. Упрощенный подход.Скачать

Расстановка Коэффициентов в Химических Реакциях // Подготовка к ЕГЭ по ХимииСкачать

Тренировки раньше и сейчас #batya #батя #тренировки #орехов #виталяорехов #раньшебылолучшеСкачать

Способы выражения концентрации растворов. 8 класс.Скачать

Коробов М. В. - Физическая химия. Часть 1 - Фазовая диаграмма воды. Закон Рауля. Закон ГенриСкачать

Задача на приготовление растворов методом "КРЕСТА". Включает См и массовую долю р-ров.Скачать

Ионные уравнения реакций. Как составлять полные и сокращенные уравненияСкачать

Задача на разбавление уксусного ангидрида уксусной кислотой. Органика. Олимпиада.Скачать

Химия | Тепловой эффект химической реакции (энтальпия)Скачать