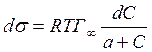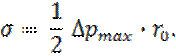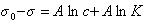Уравнение шишковского физический смысл констант уравнения шишковского (8 видео)

Методы определения поверхностного натяжения жидкостей

ОПРЕДЕЛЕНИЕ ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ РАСТВОРОВ ПОВЕРХНОСТНО-АКТИВНЫХ ВЕЩЕСТВ СТАЛАГМОМЕТРИЧЕСКИМ МЕТОДОМ

ЦЕЛЬ: Научиться определять поверхностное натяжение жидкостей сталагмометрическим методом. Построение изотерм поверхностного натяжения для растворов различных спиртов. Определение зависимости поверхностного натяжения растворов ПАВ одного гомологического ряда от концентрации; вычисление констант уравнения Шишковского; проверка правила Траубе-Дюкло.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Физико-химические особенности поведения дисперсных систем в жидких средах определяются процессами, протекающими на поверхности раздела между составляющими систему фазами, и свойствами граничных слоев, поскольку величина поверхности раздела фаз в таких системах относительно велика.

Молекулы на границах раздела фаз не полностью окружены другими молекулами того же вида по сравнению с соответствующими молекулами в объеме фазы, поэтому поверхность раздела фаз в межфазном поверхностном слое всегда является источником силового поля. Результат этого явления – нескомпенсированность межмолекулярных сил и наличие внутреннего или молекулярного давления. Для увеличения площади поверхности необходимо вывести молекулы из объемной фазы в поверхностный слой, совершив работу против межмолекулярных сил. Если процесс обратим и проходит в изотермических условиях, то затраченная работа равна увеличению свободной поверхностной энергии на границе раздела фаз по сравнению с энергией в объеме.

Приращение свободной поверхностной энергии при увеличении поверхности на 1 см 2 представляет собой удельную свободную энергию и обозначается символом σ. Величину σ называют также поверхностным натяжением и рассматривают как силу, стягивающую поверхность.

Зависимость поверхностного натяжения от концентрации ПАВ.

Зависимость поверхностного натяжения ПАВ от концентрации водных растворов хорошо описывается уравнением Шишковского, которое было получено им эмпирическим путем при исследовании растворов гомологов предельных жирных кислот на границе с собственным паром:

где А и В — эмпирические постоянные, причем величина В постоянна для всего гомологического ряда, а величина А возрастает в 3 — 3,5 раза при переходе к каждому последующему гомологу.

Определить физический смысл постоянных уравнений Шишковского можно путем анализа уравнения Гиббса:

и уравнения Ленгмюра:

где Г_∞— предельная адсорбция; а = k_дес/k_адс —отношение констант скоростей адсорбции и десорбции.

Запишем уравнение Гиббса в виде:

и подставим величину Г из уравнения Ленгмюра:

Интегрируя в пределах от 0 до С, получим

Сравнив полученное уравнение с уравнением Шишковского, получаем:

B = RTГ_∞ и .

Методы определения поверхностного натяжения жидкостей

Существующие методы определения поверхностного натяжения разделяются на три основные группы:

I. Статические методы:

1) метод капиллярного поднятия;

2) метод вращающейся капли;

3) метод Вильгельми или метод уравновешивания пластинки.

II. Полустатические методы:

1) метод максимального давления образования пузырька или капли;

2) метод отрыва кольца – метод Дю-Нуи;

3) сталагмометрический метод (метод взвешивания и счета капель).

III. Динамические методы:

1) метод колеблющихся струй;

2) метод нулевой ползучести;

3) метод расщепления.

В основе большинства статических и полустатических методов измерения поверхностного натяжения лежит метод капиллярности с основополагающим уравнением Лапласа. Наиболее теоретически разработанные методы связаны с измерением разности давлений по обе стороны поверхности раздела фаз, т.е. капиллярного давления.

Поскольку кривизну поверхности измерить трудно, то ее оценивают на основании других параметров, например, связывая ее с радиусом капилляра, формирующего мениск.

Статические методы основаны на изучении устойчивого равновесного состояния, к которому самопроизвольно приходит изучаемая система, что позволяет получать истинно равновесные значения поверхностного натяжения.

Метод капиллярного поднятия основан на формуле Жюрена:

При этом применяются тонкие капилляры, что обеспечивает сфериность мениска. Этот метод может давать точность измерения поверхностного натяжения до десятых и сотых долей .

Метод вращающейся капли позволяет измерять очень низкие значения межфазного натяжения на границах двух жидкостей. В этом методе трубка, заполненная жидкостью, приводится во вращение вокруг своей оси.

Уравнение шишковского физический смысл констант уравнения шишковского

Рис. Равновесная форма вращающейся капли.

В трубку вводится капля другой жидкости с меньшей плотностью ρ₂. За счёт действия центробежных сил эта менее плотная жидкость стремится расположиться ближе к оси вращения и вытягивается в тонкий столбик. Измеряя размеры столбика и скорость вращения ω, при известной разности плотностей жидкостей (ρ₁ – ρ₂) можно определить натяжение σ межфазной поверхности.

Метод Вильгельми или метод уравновешивания пластинки. Закреплённую на коромысле весов тонкую пластину шириной d погружают в жидкость. Пластина хорошо смачивается этой жидкостью. На поверхности пластина с обеих сторон образуются мениски. Их форма и максимальная высота поднятия определяется уравнением Лапласа.

Рис. Условие равновесия при изменении поверхностного натяжения по методу Вильгельми.

Суммарный вес поднятой жидкости на единицу длины периметра пластины не зависит от формы мениска и при нулевом краевом угле смачивания равен поверхностному натяжению σ.

где F — сила, которую надо приложить для уравновешивания пластины;

d – ширина пластины.

Метод Вильгельма один из наиболее точных методов определения поверхностного натяжения, не требующий введения каких-либо поправок.

Если платиновая или стеклянная пластина установлена так, что её нижняя поверхность будет располагаться строго на уровне поверхности, то

где F — сила, необходимая дл преодоления сил, втягивающих пластину внутрь жидкости, т.е. для уравновешивания пластины при её возвращении в начальное положение;

l и b – ширина и толщина пластины.

Полустатические методыопределения поверхностного натяжения основаны на достижении системой некоторого равновесного состояния, но это равновесие неустойчиво

Метод максимального давления образования пузырька или капли под действием приложенного извне избыточного давления Δp через калиброванный капилляр в объём жидкости продавливается пузырёк газа или капля другой жидкости. По мере роста пузырька радиус кривизны его поверхности r уменьшается и достигает минимального значения, равного радиусу капилляра r₀, когда поверхность пузырька приобретает форму полусферы.

При r = r₀ капиллярное давление 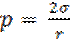достигает своего максимального значения .

Рис. Изменение радиуса кривизны поверхности пузырька при изменении поверхностного натяжения по методу наибольшего давления.

Если избыточное давления Δp меньше максимального давления , то система механически устойчива.

Если , капиллярное давление не может уравновесить приложенного давления Δp и пузырёк теряет свою устойчивость, разрастается и отрывается от поверхности, что соответствует максимальному значению перепада давления, отвечающего условию , отсюда

Метод отрыва кольца – метод Дю-Нуи основан на измерении усилия F, необходимого для отрыва от поверхгости жидкости тонкого кольца радиуса r_к хорошо смачиваемого жидкостью (θ = 0º).

В первом приближении можно считать, что значение поверхностного натяжения обратно пропорционально длине периметра кольца 2π r_к, т.е.

где 2π r_к – длина периметра кольца,

r_к – радиус кольца, измеренный от его центра до осевой линии проволоки.

Метод Дю-Нуи достаточно точен и часто используется для определения поверхностного натяжения жидкостей.

Его редко применяют для определения межфазного натяжения на границе ж – ж, поскольку в этом случае трудно реализовать условие θ = 0º.

Рис. Изменение поверхностного натяжения по методу отрыва кольца.

Сталагмометрический метод (метод взвешивания и счета капель) широко применяется для определения межфазного натяжения ж – ж. Основан на определении веса капли, отрывающейся под действием силы тяжести от плоской поверхности торцевого среза капилляра. Расчет проводят по формуле

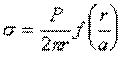
где f (r/a) – некоторая функция, определяемая из таблиц Гаркинса и Брауна; а – капиллярная постоянная.

В грубом приближении можно считать, что в момент отрыва капли её вес Р уравновешивается силами поверхностного натяжения:

где — 2π r₀ – длина окружности капилляра,

Если жидкости хорошо смачивают материал капилляра, то, пренебрегая различием между углами смачивания, можно проводить относительное измерение поверхностного натяжения, используя стандартную жидкость. В этом случае обычно принимают, что масса капли Р в момент отрыва пропорциональна поверхностному натяжению на границе раздела жидкость – пар, т.е.

где k – постоянная данного прибора.

Поверхностное натяжение σ можно вычислить, зная массу капли жидкости m в момент отрыва ее от капилляра, по уравнению:

σ= ,

где g – ускорение свободного падения, r – радиус капилляра.

Если ,где ρ – плотность жидкости, n – число капель в объёме жидкости V, вытекающей из капилляра, тогда поверхностное натяжение равно:

При калибровке сталагмометра стандартной жидкостью , поэтому

Динамические методы определения поверхностного натяжения имеют более специальное назначение, они применяются для изучения неравновесных состояний поверхностных слоёв жидкостей и скорости установления равновесной структуры их поверхности.

Метод колеблющихся струй позволяет изучать свойства поверхности жидкости через очень малые промежутки времени после их образования.

Метод нулевой ползучести для пластичных твёрдых тел вблизи точки плавления (в основном для металлов).

Метод расщепления по плоскости спайности для хрупких твёрдых тел, особенно монокристаллов с хорошо выраженной спайностью.

Для правильного выбора метода исследования растворов мицеллообразущих полуколлоидных, высокомолекулярных и типичных коллоидных поверхностно-активных веществ (высшие гомологи мыл, красители, белковые вещества) решающее значение имеет учет явлений, определяющих кинетику достижения равновесных (наименьших) значений поверхностного натяжения. Эта кинетика вызывается малой скоростью процесса формирования адсорбционных слоев, связанной с медленной диффузией сложных молекул из объема к поверхности, ориентацией их в поверхностном слое (двумерная миграция), явлениями коллоидного старения. Явления старения связаны с появлением в адсорбционном слое и прилегающих к нему слоях жидкости сплошной сетчатой (гелеобразной) структуры с явно выраженными упругопластичными вязкими свойствами.

Если эти свойства достаточно сильно развиты, то пленка становится упругой (твердой) и любые измерения поверхностного натяжения, требующие достаточной подвижности поверхности раздела, становятся неосуществимыми.

Поэтому, чтобы получить в таких растворах истинные равновесные значения поверхностного натяжения, лучше пользоваться статическими методами. Однако и некоторые полустатические методы (как, например, метод наибольшего давления пузырька или капли) вполне пригодны для этой цели, обладая при этом преимуществом простоты и удобства измерений.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ.

Оборудование и реактивы.Химические стаканы вместимостью 50 мл; сталагмометры; пипетки вместимостью 5 мл резиновая груша; исследуемые жидкости (спирты: изопропиловый, изобутиловый, изоамиловый) и стандартная жидкость (дистиллированная вода).

Поверхностное натяжение растворов определяют сталагмометрическим методом, который заключается в отсчете капель при медленном вытекании исследуемой жидкости из капилляра. В данной работе используется относительный вариант метода, когда одна из жидкостей (дистиллированная вода), поверхностное натяжение которой при данной температуре точно известно, выбирается в качестве стандартной. Сталагмометр представляет собой стеклянную трубку с расширением посередине и капилляром в нижней части; расширенная часть ограничена двумя метками.

1. Отмеряют в химический стаканчик 2,5 мл дистиллированной воды. Поместив капилляр в стаканчик с дистиллированной водой, при помощи резиновой груши затягивают раствор в прибор (уровень жидкости должен быть чуть выше верхней метки) и дают жидкости по каплям вытекать из сталагмометра в стаканчик. Когда уровень жидкости достигнет верхней метки, начинают отсчет капель; отсчет продолжают до достижения уровнем нижней метки. Эксперимент повторяют 3 раза. Для расчета поверхностного натяжения используют среднее значение n.

2. Повторяют эксперимент для каждой исследуемой жидкости.

3. Готовят растворы заданных спиртов с разной концентрацией методом разбавления.

Расчет поверхностного натяжения исследуемой жидкости производят по формуле:

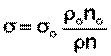
где σ_o, ρ_o, n_o — поверхностное натяжение, плотность, число капель для дистиллированной воды; σ, ρ, n — соответствующие величины для исследуемого раствора.

Стандартной жидкостью в нашем случае является вода, зависимость поверхностного натяжения которой от температуры (°С) имеет следующий вид:

В данной работе используются разбавленные растворы, поэтому можно принять, что ρ = ρ_o и вести расчет по формуле:

Результаты эксперимента для каждого из спиртов заносят в таблицу 1. По полученным данным строят изотермы поверхностного натяжения исследуемых растворов, начиная от σ = σ_o (рис. 1)

Рис. 1. Изотерма поверхностного натяжения.

По углу α (см. рис. 1) наклона касательной, проведенной к изотерме поверхностного натяжения в точке С = 0, σ = σ_o, определяют поверхностную активность G_i каждого из спиртов (G_i = — tg α) которая в данном случае будет численно равна отношению длины отрезка а к длине отрезка b (рис. 1). Длины отрезков берутся в единицах шкалы соответствующей оси координат. Сравнивая полученные значения G_i, делают вывод о влиянии длины углеводородного радикала на поверхностную активность спиртов и применимости правила Траубе-Дюкло к гомологическому ряду одноатомных спиртов.

спирт

С, моль/л

n, шт.

σ, Н/м

G_i

Для вычисления констант уравнения Шишковского строят график в координатах σ_о – σ = f(lnC). Полученные экспериментальные данные используют для нахождения констант А и В в уравнении Шишковского:

σ = σ₀ — B ln (AC + 1)

При АС >> 1 уравнение принимает вид:

σ₀ — σ = B ln A + B ln С

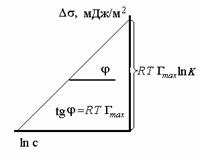
Величины А и В находят из графика зависимости σ — σ₀= f(C) (рис. 2).

Рис. 2. Графическое определение постоянных А и В в уравнении Шишковского.

Угловой коэффициент наклона прямолинейного участка построенной кривой равен В = tg α. Для определения константы А экстраполируют полученную прямую до оси абсцисс.

1. Определить сталагмометрическим методом поверхностное натяжение серий растворов спиртов различной концентрации. Выполнить расчёт поверхностного натяжения спиртов двумя способами: через количество петель и через массу капли.

ρ (изопропил. сп.) = 0,7851 г/см 3 (20°С)

ρ (изобутил. сп.) = 0,8027 г/см 3 (20°С)

ρ (изоамил. сп.) = 0,814 г/см 3 (20°С)

2. Построить изотерму поверхностного натяжения для каждого из спиртов.

3. Определить поверхностную активность каждого из спиртов. Сделать вывод о влиянии длины углеводородного радикала на поверхностную активность спиртов и о применимости правила Траубе-Дюкло к гомологическому ряду одноатомных спиртов.

4. Определить графическим способом константы уравнения Шишковского.

Содержание

1.5. Поверхностное натяжение растворов и адсорбция
Физическая химия
Главная > Документ
§4. Мономолекулярная адсорбция. Изотерма адсорбции Ленгмюра
§5 . Теория полимолекулярной адсорбции БЭТ
§6. Изотермы адсорбции и поверхностного натяжения растворов ПАВ Уравнение Шишковского
§7. Классификация и общая характеристика поверхностно-активных веществ. Правило Дюкло – Траубе
🔥 Видео

Видео:Поверхностные явления: адгезия, смачивание, адсорбция | Коллоидная химияСкачать

1.5. Поверхностное натяжение растворов и адсорбция

Свободная поверхностная энергия самопроизвольно может только уменьшаться, что проявляется в уменьшении либо поверхности раздела фаз, либо межфазного (поверхностного) натяжения. Поверхностное натяжение может уменьшаться в результате самопроизвольного перераспределения компонентов системы между объемами фаз a и b и поверхностью их раздела. В поверхности раздела фаз будут преимущественно концентрироваться те компоненты, которые способны уменьшать избыточную свободную поверхностную энергию. Это явление получило название «адсорбция». Количественно мерой адсорбции служит избыток вещества в поверхностном слое определенной толщины по сравнению с его количеством в таком же слое в объеме фазы. Этот избыток обычно относят к единице площади поверхности (или к единице массы адсорбента). Такая адсорбция называется гиббсовской и обозначается буквой Г_i. Поверхностный избыток является алгебраической величиной. Если он положителен, то вблизи поверхности данный компонент присутствует в избытке, если отрицателен, то концентрация компонента на поверхности фазы ниже, чем в ее объеме .

Рассмотрим распределение в системе i -го компонента, предполагая, что это вещество способно понижать поверхностное натяжение. В соответствии с уравнением (1.1.6) число молей n вещества i-го компонента в системе определяется как .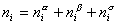

Количество вещества в обеих фазах составляет

. (1.1.81)

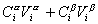
где С a , С b — концентрация вещества в фазах a, b.

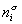
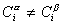
Количество вещества на поверхности раздела фаз , избыточное по отношению к объемам фаз V a и V b , оказывается зависимым от положения разделяющей плоскости, так как концентрации вещества в различных фазах не равны, .

Учитывая уравнение (1.1.81) ,

. (1.1.82)

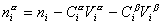
Разделив выражение (1.1.82) на площадь поверхности раздела фаз А, можем определить гиббсовскую адсорбцию:

. (1.1.83)

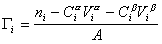
Фундаментальным уравнением физической химии поверхностей является взаимосвязь между адсорбцией и межфазным натяжением, которую можно определить экспериментально при одновременном изменении многих факторов. Остановимся на системах, в которых адсорбция протекает при постоянной температуре. Связь между адсорбцией и межфазным натяжением при постоянной температуре T называется изотермой адсорбции, фундаментальное уравнение которой известно как уравнение Гиббса. Рассмотрим его вывод.

При небольшом обратимом изменении энергии системы dU с учетом формулы (1.1.4) можем написать

, (1.1.84)

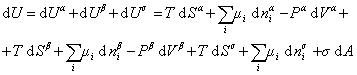
где U – полная внутренняя энергия системы; U a , U b , U s – внутренняя энергия фаз aиb и поверхности их раздела; P a , P b — давление в фазах aиb; m — химический потенциалi-того компонента; S a , S b , S s – энтропия фаз a иb и их поверхности раздела; s — поверхностное натяжение.

Поскольку из курса химической термодинамики известно, что

(1.1.85)

, (1.1.86)

. (1.1.87)

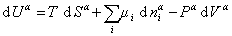
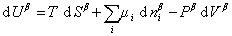
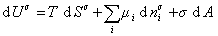
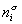
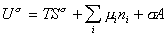
Если энергию, энтропию и количество компонентов увеличивать от нуля до некоторого определенного значения при постоянстве температуры T, площади поверхности раздела фаз A и количестве вещества на этой поверхности , то уравнение (1.1.87) переходит в общее уравнение

, (1.1.88)

дифференцирование которого приводит к выражению

. (1.1.89)

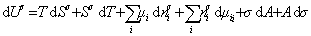
Сравнивая его с уравнением (1.1.88), получаем

. (1.1.90)

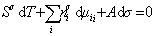
В расчете на единицу поверхности

, (1.1.91)

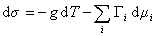
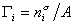
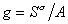
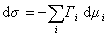
где – гиббсовская адсорбция; – удельная энтропия поверхностного слоя.

. (1.1.92)

Для двухкомпонентной системы

, (1.1.93)

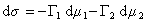
где индекс 1 относится к растворителю, а индекс 2 – к растворенному веществу.

Рис. 1.15. Схема реальной (I) межфазовой области и идеальной (II) и (III) разделяющей межфазовой поверхности (поверхности Гиббса)

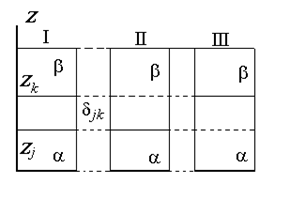
Разделяющая поверхность Гиббса может быть проведена так, чтобы обратилась в нуль адсорбция любого наперед заданного компонента, но только одного, как это показано на рис. 1.15.

Расстояние между двумя плоскостями (разделяющими поверхностями), одна из которых соответствует условию Г_j = 0, а другая — Г_k = 0, обозначим d_kj:

, (1.1.94)

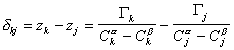
где Г_k, Г_j– избытки рассматриваемых компонентов в поверхностном слое ; C_k a , C_k b , C_j a , C_j b – концентрация компонентов k и j в фазах a и b; z_k, z_j – координаты разделяющей поверхности.

Поскольку значения Г₁ в уравнении (1.1.93) определены относительно произвольно выбранного положения разделяющей плоскости, то ее можно расположить так, чтобы избыток растворителя в поверхностном слое был равен нулю ( Г₁ = 0).

, (1.1.95)

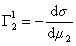
где верхний индекс 1 означает, что для выбранной поверхности раздела Г₁=0.

, (1.1.96)

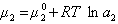
получаем после дифференцирования уравнения (1.1.96)

, (1.1.97)

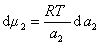
где 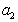— активность растворенного вещества.

Поэтому, подставляя уравнение (1.1.97) в уравнение (1.1.95), получаем

. (1.1.98)

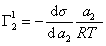
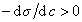
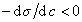
Из уравнения (1.1.98) следует, что если , то адсорбция положительна, а при возникает дефицит растворенного вещества на разделяющей поверхности .

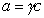
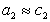
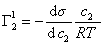
Поскольку , где g – коэффициент активности, который для разбавленных растворов стремится к единице, то и

. (1.1.99)

Уравнение (1.1.99) представляет собой наиболее употребляемую форму изотермы адсорбции Гиббса, причем так как рассматривается адсорбция именно растворенного вещества, индексы при адсорбции и концентрации опускают, т.е.

. (1.1.100)

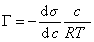
Исследования показывают, что существуют такие вещества, растворение которых приводит к резкому снижению поверхностного натяжения раствора. Эти вещества называют поверхностно-активными. В соответствии с уравнением Гиббса адсорбция их всегда положительна, т.е. концентрация в поверхностном слое выше объемной концентрации. По предложению Ребиндера мера поверхностной активности обозначается первой буквой фамилии Гиббса. Обычно используют значения поверхностной активности в бесконечно разбавленных растворах

. (1.1.101)

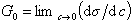
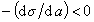
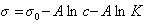
К классу поверхностно-активных веществ (ПАВ) относятся жирные кислоты и их соли (мыла), сульфокислоты, их соли, спирты, алкилсульфоэфиры и др. Если , то Г >1, то единицей в уравнении Шишковского (1.1.105 ) можно пренебречь, тогда

. (1.1.106)

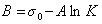
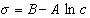
Обозначим постоянной В постоянные при изотермических условиях величины , тогда

. (1.1.107)

Следовательно, при относительно высокой концентрации растворов ПАВ их поверхностное натяжение должно уменьшаться экспоненциально с увеличением концентрации.

Уравнение (1.1.107) может быть получено непосредственно из уравнения изотермы адсорбции Гиббса:

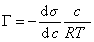
При достаточно высокой концентрации растворенного вещества адсорбция достигает предела , т.е. Г = Г_max , поэтому

, (1.1.108)

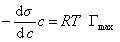
где при постоянной температуре правая часть представляет собой постоянную величину и может быть обозначена RT Г_max = A. Следовательно,

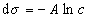
откуда после интегрирования получаем

. (1.1.109)

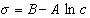
Таким образом, уравнение Шишковского может быть выведено из уравнения Гиббса, так как уравнения (1.1.107) и (1.1.109) идентичны. Точность уравнения Шишковского связана с тем, что в нем уже заложено условие насыщения адсорбционного слоя.

Если уравнение Шишковского в форме

(1.1.110)

, (1.1.111)

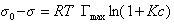
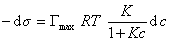
и подставить в уравнение Гиббса величину

, (1.1.112)

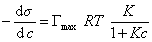
то уравнение изотермы адсорбции примет вид

. (1.1.113)

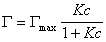
В такой форме уравнение изотермы адсорбции носит название изотермы Ленгмюра. Американский ученый И. Ленгмюр в 1917 г. развил представление о мономолекулярной адсорбции и на основании молекулярно- кинетической теории получил уравнение (1.1.113) .

Уравнение Шишковского позволяет определить предел адсорбции (при Kc>>1), так как в таком случае это уравнение принимает вид

. (1.1.114)

Рис. 1.16. Зависимость поверхностного натяжения от концентрации растворов ПАВ в координатах уравнения Шишковского

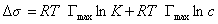
Построив график 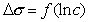, как это показано на рис. 1.16, по углу наклона можно определить предел адсорбции, а по отрезку, отсекаемому наклонной линией на оси ординат при ln c = 0, рассчитать постоянную равновесия процесса адсорбции K.

Понимание адсорбционных процессов имеет чрезвычайно важное значение, так как они лежат в основе многих процессов, протекающих на границе раздела фаз, например крашения, отмывания загрязнений, отделки текстильных материалов и т.д., т.е. в основе всех коллоидно -химических процессов на границе жидкость–газ.

Видео:Коллоидная химия. Лекция 1. Физико-химия поверхностных явленийСкачать

Физическая химия

Главная > Документ

Информация о документе
Дата добавления:
Размер:
Доступные форматы для скачивания:

§4. Мономолекулярная адсорбция. Изотерма адсорбции Ленгмюра

Чтобы получить теоретическую изотерму адсорбции, описывающую широкую область концентраций, необходимо использование представлений о механизме адсорбции и конкретных моделей.

Адсорбция рассматривается как квазихимическая реакция между адсорбатом и адсорбционными центрами поверхности адсорбента. В этом заключается основная идея адсорбционной теории Ленгмюра, которая явилась фундаментальным вкладом в учение об адсорбции. Ограниченность поверхности адсорбента приводит к её адсорбционному насыщению по мере увеличения концентрации распределяемого вещества. Это положение теории Ленгмюра уточняется следующими допущениями: 1) адсорбция локализована (молекулы не перемещаются по поверхности) на отдельных адсорбционных центрах, каждый из которых взаимодействует только с одной молекулой адсорбата; в результате образуется мономолекулярный слой; 2) адсорбционные центры энергетически эквивалентны – поверхность адсорбента эквипотенциальна; 3) адсорбированные молекулы не взаимодействуют друг с другом. 4) адсорбция обратима.

Для получения уравнения изотермы обратимся к основному положению теории Ленгмюра. Примем, что при адсорбции происходит квазихимическая реакция между распределяемым компонентом и адсорбционными центрами поверхности:

↔

где – адсорбционные центры поверхности; В – распределяемое вещество; – комплекс, образующийся на поверхности.

По мере увеличения концентрации (давления) вещества В реакция сдвигается в сторону образования комплекса и свободных адсорбционных центров становится меньше. Константа адсорбционного равновесия равна

(IX.6)

В этом соотношении

(IX.7)

где А – величина адсорбции вещества В ; A  — емкость адсорбционного монослоя, или число адсорбционных центров, приходящихся на единицу площади поверхности (или на единицу массы адсорбента); А 0 – число оставшихся свободными адсорбционных центров, приходящихся на единицу площади поверхности (или на единицу массы адсорбента).

Подставляя уравнения (IX.7) в уравнение (IX.6), получим:

Опуская индекс при обозначении концентрации адсорбата С В , после простых преобразований окончательно имеем:

(IX.8)

Выражение (IX.8) называется уравнением изотермы мономолекулярной адсорбции Ленгмюра. Так как концентрации газов и паров практически пропорциональны парциальным давлениям, то для них изотерма адсорбции Ленгмюра принимает вид:

(IX.9)

Необходимо отметить, что константа адсорбционного равновесия в уравнении Ленгмюра характеризует энергию взаимодействия адсорбата с адсорбентом. Чем сильнее это взаимодействие, тем больше константа адсорбционного равновесия .

Адсорбционное уравнение Ленгмюра часто представляют относительно степени заполнения поверхности – отношения величины адсорбции А к емкости монослоя А 

(IX.10)

Типичная изотерма адсорбции Ленгмюра показана на рис.20.

Рис.20. Изотерма адсорбции Ленгмюра

Важны экстраполяционные следствия из соотношений (IX.8) – (IX.9). При малых концентрациях или давлениях, когда С  0, получаем:

и (IX.11)

Выражения (IX.11) соответствуют закону Генри: величина адсорбции линейно растет с увеличением концентрации.

При больших концентрациях и давлениях, когда КC >> 1 и KP >> 1, уравнения (IX.8) – (IX.9) переходят в соотношения:

и (IX.12)

Соотношения (IX.12) отвечают состоянию насыщения, когда вся поверхность адсорбента покрывается мономолекулярным слоем адсорбата. Экспериментальное определение А  позволяет рассчитать удельную поверхность адсорбента (поверхность единицы массы адсорбента):

(IX.12a)

где А  -предельная адсорбция, выражаемая числом молей адсорбата на единицу массы адсорбента; N A – число Авогадро; – площадь, занимаемая одной молекулой адсорбата.

Экспериментальные результаты по определению изотермы адсорбции обычно обрабатывают с помощью уравнения Ленгмюра, записанного в линейной форме (числитель (IX.8) переносят в знаменатель, а знаменатель – в числитель):

(IX.13)

Если обе части уравнения (IX.13) умножить на С, то получим ещё одну форму записи указанного уравнения, дающего линейную зависимость в координатах и С:

(IX.13а)

Такая линейная зависимость позволяет графически определить оба постоянных параметра ( А  и К ) адсорбционной изотермы. На рис.21 представлена типичная изотерма адсорбции в координатах уравнения (IХ.13а). Экстраполяция зависимости до оси ординат дает отрезок, равный 1/( А  K ), а тангенс угла наклона прямой к оси абсцисс равен 1/ А  ,

Рис.21. Изотерма адсорбции в координатах линейной формы уравнения Ленгмюра (IX.13а)

При адсорбции газов из их смесей в соответствии с уравнением изотермы Ленгмюра величины адсорбции суммируются, а концентрация свободных центров A 0 является общей для равновесной многокомпонентной системы.

Степень заполнения для i — o го компонента составит:

(IX.14),

где P i – парциальное давление i — o го компонента, а K i – его адсорбционная константа равновесия.

Из уравнения (IX.14) следует, что увеличение парциального давления одного компонента подавляет адсорбцию других, и тем сильнее, чем больше его адсорбционная константа равновесия.

Все рассмотренные до сих пор уравнения справедливы для мономолекулярной адсорбции, протекающей на адсорбенте с энергетически эквивалентными адсорбционными центрами. Однако реальные поверхности твердых тел, как правило, не обладают такими свойствами. Для приближения к реальным условиям целесообразно рассмотрение возможных распределений адсорбционных центров поверхности адсорбента по энергиям. Приняв экспоненциальное распределение адсорбционных центров по энергиям, в области средних заполнений получается найденное эмпирически уравнение Фрейндлиха :

(IX.15)

где К и п – постоянные.

Уравнение Фрейндлиха широко используется при обработке экспериментальных адсорбционных данных, в том числе в инженерных расчётах. Чаще всего оно применяется в логарифмической форме

позволяющей построить линейную зависимость ln A – ln P и графически определить оба постоянных параметра K и п.

§5 . Теория полимолекулярной адсорбции БЭТ

Уравнение Ленгмюра можно использовать только при условии, что адсорбция вещества сопровождается образованием мономолекулярного слоя. Это условие выполняется достаточно строго в случае хемосорбции, физической адсорбции газов при небольших давлениях и температурах выше критической (без конденсации на поверхности адсорбента), а также при адсорбции из растворов. Указанное ограничение для применения уравнения Ленгмюра связано не столько с формальным описанием адсорбции, сколько с невозможностью получить правильные значения параметров K и А  , соответствующих их физическому смыслу.

В большинстве случаев мономолекулярный адсорбционный слой не компенсирует полностью избыточную поверхностную энергию и влияние поверхностных сил может распространяться на второй, третий и последующие адсорбционные слои. Эта возможность реализуется, когда газы и пары адсорбируются при температурах ниже критической. В этом случае образуются полимолекулярные слои вещества на поверхности адсорбента. Полимолекулярную адсорбцию можно представить как результат вынужденной конденсации пара под действием поверхностных сил. Если в области образования мономолекулярного слоя величина адсорбции существенно замедляет свой рост с увеличением давления пара, то в области давлений, близких к давлению насыщенного пара, она начинает резко возрастать и адсорбция заканчивается объёмной конденсацией пара при P =Р 0 (иногда используется обозначение P s ) (рис.22).

Рис.22 . Изотерма полимолекулярной адсорбции

Первые попытки получения уравнения изотермы полимолекулярной адсорбции были сделаны ещё Ленгмюром. Современная форма уравнения полимолекулярной адсорбции была предложена Брунауэром, Эмметом и Теллером. В соответствии с начальными буквами фамилий авторов обсуждаемая теория получила название теории БЭТ. В этой теории дополнительным допущением к тем, которые были положены в основу вывода уравнения изотермы Ленгмюра, является представление об образовании на поверхности адсорбента «последовательных комплексов» – адсорбционных центров с одной, двумя, тремя и т. д. молекулами адсорбата.

Величина адсорбции компонента В равна

(IX.16)

где С – константа уравнения, а P 0 – давление насыщенного пара компонента В при данной температуре.

Соотношение (IX.16) является основным уравнением обобщенной теории Ленгмюра и называется уравнением полимолекулярной адсорбции БЭТ. С уменьшением давления при P / P 0 1 уравнение БЭТ превращается в уравнение мономолекулярной адсорбции Ленгмюра, которое при дальнейшем уменьшении давления ( P  0) переходит в закон Генри.

При обработке экспериментальных результатов уравнение БЭТ обычно используют в линейной форме.

На теории БЭТ основан стандартный метод измерения удельной поверхности адсорбентов, катализаторов, порошков и других материалов (метод БЭТ). По экспериментальным данным находят величину A  , а затем по уравнению (IX.12a) рассчитывают удельную поверхность. В качестве адсорбатов используют инертные газы (азот, аргон, криптон и др.), которые проявляют слабое межмолекулярное взаимодействие на поверхности адсорбента, что находится в соответствии с исходными допущениями теории и обеспечивает достоверность получаемых результатов. Значения площади, занимаемой молекулой адсорбата в заполненном монослое принимают равной для азота 0,162 нм 2 , аргона – 0,138 нм 2 , криптона – 0,195 нм 2 . Для увеличения адсорбции таких газов ее ведут при низких температурах, откуда и частое название метода БЭТ – метод низкотемпературной адсорбции.

§6. Изотермы адсорбции и поверхностного натяжения растворов ПАВ
Уравнение Шишковского

Поверхностно-активные вещества (ПАВ), молекулы которых имеют дифильное строение и включают большой углеводородный радикал, отличаются высокой поверхностной активностью по отношению к воде, что отражает сильную зависимость поверхностного натяжения водного раствора ПАВ от их концентрации. Большие значения поверхностной активности предполагают пренебрежимо малые концентрации ПАВ в объеме раствора по сравнению с их концентрацией в поверхностном слое, т. е. с величиной их адсорбции на границе раствор – воздух. Подобная зависимость может обнаруживаться и в растворах других веществ на границе с жидкостью или твёрдым телом, например при специфическом взаимодействии с поверхностью. Отмеченная особенность позволяет пренебречь разницей между величиной адсорбции A и величиной гиббсовской адсорбции Г, т. е. будем полагать, что Г  A . Из этого соотношения следует, что для растворов ПАВ все уравнения адсорбции, включающие величину адсорбции A , будут также справедливы, если заменить А на Г.

Обратимся к уравнению изотермы адсорбции Лэнгмюра (IХ.8). Учитывая соотношение Г  A , величину адсорбции можно приравнять к её выражению из уравнения Гиббса (IX.3)

После разделения переменных имеем:

Проинтегрируем полученное выражение в пределах от 0 до С и от (поверхностное натяжение чистого растворителя) до :

так как Kd С= d (1 + K С ) .

После интегрирования получим уравнение Шишковского , характеризующее поверхностное натяжение растворов ПАВ в зависимости от концентрации:

(IX.17)

Подобную зависимость от С для ПАВ Б.А.Шишковский получил опытным путём в следующем виде:

, где a и b – константы.

Ленгмюр, связав уравнение Гиббса со своим уравнением, определил физический смысл констант эмпирического уравнения Шишковского. Одна из них ( a ) равна произведению A  RT , другая ( b ) имеет смысл константы адсорбционного равновесия K в уравнении Ленгмюра. Допущения, принятые при выводе уравнения Шишковского, показывают, что это уравнение в отличие от уравнений Гиббса и Ленгмюра справедливо только для поверхностно-активных веществ, обладающих высокой поверхностной активностью.

В соответствии с уравнением Шишковского при малых концентрациях ПАВ в растворе поверхностное натяжение снижается резко, но с ростом концентрации степень его снижения уменьшается и стремится к постоянному значению. Из вывода уравнения Шишковского следует, что такой ход зависимости от С обусловлен теми же причинами, что и снижение прироста адсорбции, а именно уменьшением концентрации свободных от ПАВ адсорбционных центров. Уравнение Шишковского, как и уравнение Ленгмюра, не учитывает взаимодействия молекул ПАВ на поверхности.

Дальнейшее увеличение концентрации ПАВ с большой поверхностной активностью может привести к появлению мицелл в растворе и на межфазной поверхности, что равнозначно возникновению новой фазы (механизм образования мицелл ПАВ рассматривается ниже), поэтому характер изменения величины адсорбции с увеличением концентрации ПАВ становится иным.

§7. Классификация и общая характеристика поверхностно-активных веществ. Правило Дюкло – Траубе

Наличие гидрофильной и олеофильной (гидрофобной) частей у молекул ПАВ является характерной отличительной особенностью их строения. По способности к диссоциации в водных растворах поверхностно-активные вещества делят на ионогенные и неионогенные. В свою очередь ионогенные ПАВ подразделяют на анионные, катионные и амфолитные (амфотерные).

Анионные ПАВ диссоциируют в воде с образованием поверхностно-активного аниона. К ПАВ этого типа, составляющего большую часть мирового производства всех поверхностно-активных веществ, относятся:

а) карбоновые кислоты и их соли (мыла) общей формулы RCOOM (где М – одновалентный металл), например пальмитат натрия C 15 H 31 COONa, стеарат натрия C 17 H 35 COONa, олеат натрия C 17 H 33 COONa;

б) алкилсульфаты ROSO 2 OM;

в) алкиларилсульфонаты RArSO 2 OM;

г) вещества, содержащие другие типы поверхностно-активных анионов, например фосфаты, тиосульфаты и т. д..

В кислых средах соли карбоновых кислот переходят в слабодиссоциированные и малорастворимые кислоты, а в присутствии некоторых катионов (кальция, магния) образуют нерастворимые соли, что резко снижает эффективность их действия как ПАВ, особенно ухудшает их моющее действие. Большими преимуществами в этом отношении обладают алкилсульфаты и алкилсульфонаты, которые являются солями сильных кислот и поэтому могут быть использованы в кислых и солевых растворах.

Катионные ПАВ диссоциируют в воде с образованием поверхностно-активного катиона. К катионным ПАВ относятся:

а) соли первичных, вторичных и третичных алифатических и ароматических аминов;

б) соли алкилзамещенных аммониевых оснований и т. д.

Катионные ПАВ – наиболее токсичные и наименее биологически разлагаемые из всех ПАВ; их часто используют в качестве бактерицидных, фунгицидных, дезинфицирующих веществ, ингибиторов коррозии.

Амфолитные ПАВ содержат две функциональные группы, одна из которых имеет кислый, а другая оснóвный характер, например карбоксильную и аминную группы. В зависимости от рН среды амфолитные ПАВ проявляют анионактивные или катионактивные свойства:

Неионогенные ПАВ не диссоциируют в растворах на ионы. Методы их получения основаны на реакции присоединения этиленоксида к спиртам, карбоновым кислотам, аминам и другим соединениям. Например, оксиэтилированные алкилспирты марки «ОС» синтезируют по реакции:

ROH + nH 2 C—CH 2  RO(CH 2 CH 2 O) n H

Полиоксиэтиленовая цепь определяет гидрофильные свойства неионогенных ПАВ. Изменяя длину полиоксиэтиленовой цепи, легко регулировать их коллоидно-химические свойства. Эти ПАВ применяются в любых средах (кислой и щелочной), а также в присутствии растворимых солей. Полиоксиэтиленовые эфиры алкилфенолов марки ОП обладают хорошими моющими свойствами.

К недостаткам этих ПАВ относится медленное разложение из-за наличия в их составе ароматического радикала и, как следствие, накопления их в объектах окружающей среды. Неионогенные ПАВ с алкильными радикалами способны биологически разлагаться достаточно полно и быстро.

Все дифильные поверхностно-активные вещества относительно поведения их в воде делят на истинно растворимые и коллоидные.

К первой группе относится большой класс растворимых в воде дифильных органических соединений с небольшим углеводородным радикалом, например низшие спирты, фенолы, кислоты и их соли, амины. Вещества этого типа в растворе находятся в молекулярно-дисперсном состоянии вплоть до концентраций, соответствующих их насыщенным растворам и разделению системы на две сплошные фазы. Эти вещества применяются в качестве смачивателей вспенивателей, гидрофобизаторов при флотации, диспергаторов, облегчающих процессы образования новых поверхностей, и т. д.

Особый интерес представляют коллоидные поверхностно-активные вещества. Именно они в первую очередь понимаются под термином ПАВ. Главной отличительной особенностью этих веществ является способность образовывать термодинамически устойчивые (лиофильные) гетерогенные дисперсные системы(ассоциативные или мицеллярные коллоиды). К основным свойствам коллоидных ПАВ, обусловливающим их широкое применение, относятся высокая поверхностная активность; способность к самопроизвольному мицеллообразованию – образованию лиофильных коллоидных растворов при концентрации ПАВ выше некоторого определенного значения, называемого критической концентрацией мицеллообразования (ККМ); способность к солюбилизации – резкому увеличению растворимости веществ в растворах коллоидных ПАВ вследствие их «внедрения» внутрь мицеллы; высокая способность стабилизировать различные дисперсные системы.

Поверхностная активность коллоидных ПАВ зависит, главным образом, от длины углеводородного радикала. Увеличение длины радикала на одну группу -СН 2 — приводит к возрастанию поверхностной активности приблизительно в 3,2 раза ( правило Дюкло – Траубе ). Это правило соблюдается в основном для истинно растворимых ПАВ.

Для органических сред правило Дюкло – Траубе обращается: поверхностная активность снижается с увеличением длины углеводородного радикала ПАВ.

В заключение можно отметить, что основной количественной характеристикой ПАВ является поверхностная активность, которая определяет их способность понижать поверхностное натяжение, вызывать эмульгирование, пенообразование, диспергирование и стабилизацию, смачивание и другие явления.