Уравнение сферы в начале координат (5 видео)

Сфера, шар, сегмент и сектор. Формулы и свойства сферы

Формула. Объём шара:

V =	4	π R 3 =	1	π D 3
	3		6

S = 4 π R 2 = π D 2

Содержание

Уравнение сферы
Основные свойства сферы и шара
Секущая, хорда, секущая плоскость сферы и их свойства
Касательная, касательная плоскость к сфере и их свойства
Геометрия. 11 класс
Уравнение сферы в начале координат
📽️ Видео

Видео:№577. Напишите уравнение сферы с центром А, проходящей через точку N, если: а) А ( — 2; 2; 0)Скачать

Уравнение сферы

x 2 + y 2 + z 2 = R 2

( x — x ₀) 2 + ( y — y ₀) 2 + ( z — z ₀) 2 = R 2

Видео:11 класс, 20 урок, Уравнение сферыСкачать

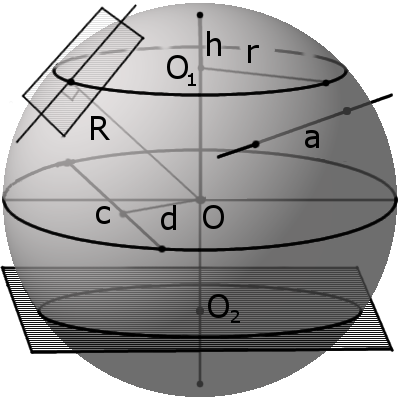
Основные свойства сферы и шара

Видео:Геометрия. 10 класс. Уравнение сферы /16.03.2021/Скачать

Секущая, хорда, секущая плоскость сферы и их свойства

d m между секущей плоскостью и центром сферы всегда меньше радиуса R:

m r такого круга можно найти по формуле:

где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.

Видео:№578. Найдите координаты центра и радиус сферы, заданной уравнением: а) х2+y2+z2 = 49; б) (x — 3)2Скачать

Касательная, касательная плоскость к сфере и их свойства

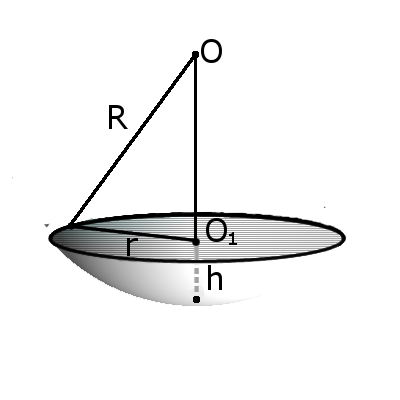
Формула. Объём сегмента сферы с высотой h через радиус сферы R:

V =	h 2 π	(3R — h )
	3

S = π R(2 h + √ 2 h R — h 2 )

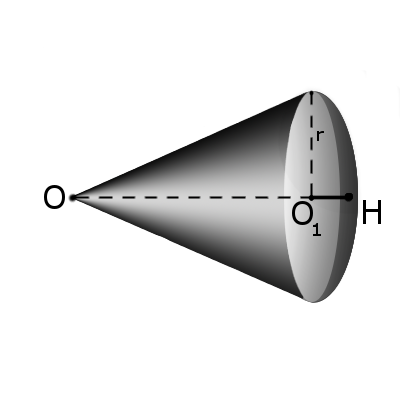
Формула. Объём сектора V с высотой O₁H (h) через радиус шара OH (R):

V =	2 π R 2 h
	3

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Видео:№579. Докажите, что каждое из следующих уравнений является уравнением сферы. Найдите координатыСкачать

Геометрия. 11 класс

Конспект урока

Геометрия, 11 класс

Урок №8. Сфера и шар

Перечень вопросов, рассматриваемых в теме:

что такое сфера, какие у неё есть элементы (центр, радиус, диаметр сферы);
что такое шар и его элементы;
уравнение сферы;
формула для нахождения площади поверхности сферы;
взаимное расположение сферы и плоскости;
теорема о радиусе сферы, который проведён в точку касания и теорему обратную данной.

Глоссарий по теме:

Окружность – множество точек плоскости, равноудалённых от данной точки. Данная точка называется центром окружности, расстояние от центра до любой точки окружности называется радиусом окружности.

Круг – это часть плоскости, ограниченная окружностью.

Сфера – это поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, которую называют центром.

Тело, ограниченное сферой, называется шаром.

Шар можно описать и иначе. Шаром радиуса R с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек.

– уравнение сферы радиуса R и центром С(x₀; y₀; z₀).

Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка – точкой касания.

Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.

Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r.

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс. 136-142.

Шарыгин И.Ф., Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений– М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 77-84.

Открытые электронные ресурсы:

Теоретический материал для самостоятельного изучения

1. Основные теоретические факты

По аналогии с окружностью сферу рассматривают как множество всех точек равноудалённых от заданной точки, но только всех точек не плоскости, а пространства.

Рисунок 1 – Сфера с центром в точке О и радиусом R

Данная точка О называется центром сферы, а заданное расстояние – радиусом сферы (обозначается R). Любой отрезок, соединяющий центр и какую-нибудь точку сферы, также называется радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через центр, называется диаметром (обозначается D). D=2R.

Сферой называется поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, которую называют центром.

Тело, ограниченное сферой, называется шаром.

Сферу можно получить ещё одним способом — вращением полуокружности вокруг её диаметра, а шар – вращением полукруга вокруг его диаметра.

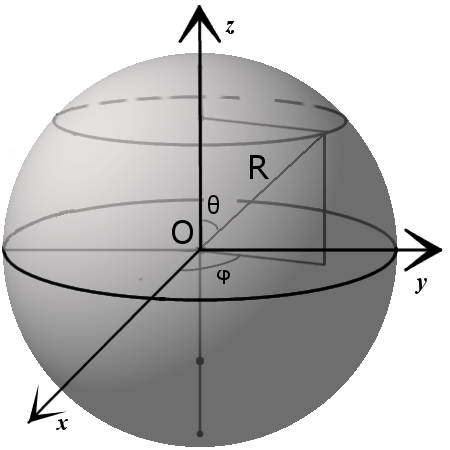
2. Уравнение сферы

Прежде чем вывести уравнение сферы введем понятие уравнения поверхности в пространстве. Для этого рассмотрим прямоугольную систему координат Oxyz и некоторую поверхность F. Уравнение с тремя переменными x, y, z называется уравнением поверхности F, если этому уравнению удовлетворяют координаты любой точки поверхности F и не удовлетворяют координаты никакой другой точки.

Пусть сфера имеет центром точку С (x₀; y₀; z₀) и радиус R. Расстояние от любой точки М (x; y; z) до точки С вычисляется по формуле:

МС=

Исходя из понятия уравнения поверхности, следует, что если точка М лежит на данной сфере, то МС=R, или МС 2 =R 2 , то есть координаты точки М удовлетворяют уравнению:

Это выражение называют уравнением сферы радиуса R и центром С(x₀; y₀; z₀).

3. Взаимное расположение сферы и плоскости

Взаимное расположение сферы и плоскости зависит от соотношения между радиусом сферы R и расстояния от центра сферы до плоскости d.

1. Пусть dR. Если расстояние от центра сферы до плоскости меньше радиуса сферы, тогда сфера и плоскость пересекаются, и сечение сферы плоскостью есть окружность.

2. Пусть d=R. Если расстояние от центра сферы до плоскости равно радиусу сферы тогда сфера и плоскость имеют только одну общую точку, и в этом случае говорят, что плоскость касается сферы.

3. Пусть dR. Если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек.

Рассмотрим случай касания более подробно.

Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка – точкой касания.

Теорема (свойство касательной плоскости).

Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.

Теорема (признак касательной плоскости):

Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащей на сфере, то эта плоскость является касательной к сфере.

4. Основные формулы

Соотношение между радиусом сферы, радиусом сечения и расстоянием от центра сферы до плоскости сечения:

Формула для вычисления площади поверхности сферы и ее элементов:

S=4πR 2 – площадь сферы.

S = 2πRh – площадь поверхности сегмента сферы радиуса R с высотой h.

– площадь поверхности сектора с высотой h.

Примеры и разбор решения заданий тренировочного модуля

1. Площадь сечения шара, проходящего через его центр, равна 9 кв. м. Найдите площадь поверхности шара.

Площадь круга вычисляется по формуле: S_кр=πR 2 .

Площадь поверхности шара вычисляется по формуле: S_сф=4πR 2 . Радиус шара и радиуса сечения, проходящего через центр шара, одинаковые. Поэтому площадь поверхности шара в 4 раза больше площади его диаметрального сечения. То есть площадь поверхности шара равна 36.

2. Вычислите радиус круга, площадь которого равна площади сферы радиуса 5.

Площадь сферы равна S_сф=4πR 2 . То есть S_сф=100π.

По условию площадь круга некоторого радиуса r также равна 100π. Значит, r 2 =100, то есть r=10.

3. Все стороны треугольника АВС касаются сферы радиуса 5. Найти расстояние от центра сферы до плоскости треугольника, если АВ=13, ВС=14, СА=15

Окружность, вписанная в треугольник, является сечением сферы.

Найдем ее радиус.

Площадь треугольника с известными сторонами можно вычислить по формуле Герона:

С другой стороны, S=p·r.

Теперь найдем расстояние от центра шара до секущей плоскости.

4. Вершины прямоугольника лежат на сфере радиуса 10. Найти расстояние от центра сферы до плоскости прямоугольника, если его диагональ равна 16.

Так как вершины прямоугольника лежат на сфере, то окружность, описанная около прямоугольника, является сечением сферы.

Радиус окружности, описанной около прямоугольника, равен половине его диагонали, то есть r=8.

Видео:Уравнение сферыСкачать

Уравнение сферы в начале координат

19.1. Определения шара, сферы и их элементов

С шаром и сферой мы уже знакомы. Напомним их определения.

Определение. Шаром называется множество всех точек пространства, находящихся от данной точки на расстоянии, не большем данного R ( R > 0). Данная точка называется центром шара, а данное расстояние R — радиусом шара .

Определение. Сферой называется множество всех точек пространства, находящихся от данной точки на расстоянии, равном данному R. Данные точка и расстояние R называются соответственно центром и радиусом сферы.

На рисунке 193 изображён шар с центром О и радиусом R = OА.

Из определений шара и сферы следует, что шар с центром О и радиусом R является объединением двух множеств точек: 1) множества точек M пространства, для которых OM (они называются внутренними точками шара и образуют его внутренность); 2) множества всех М, для которых ОМ = R (эти точки являются граничными точками шара, а их объединение составляет границу шара, которая называется шаровой поверхностью и является сферой c центром О и радиусом R ) .

Радиусом шара называют также всякий отрезок, соединяющий центр шара с точкой шаровой поверхности. Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром шара . Концы любого диаметра шара называются диаметрально nротивоположными точками шара. Отрезок, соединяющий две любые точки шаровой поверхности и не являющийся диаметром шара, называют хордой шара ( сферы ) . На рисунке 193 отрезки ОА, ОВ, ON, OS — радиусы шара; отрезки АВ , NS — диаметры шара; A и B — диаметрально противоположные точки шара. Из определения диаметра шара следует, что он равен удвоенному радиусу шара.

Покажем, что шар — тело вращения. Для этого рассмотрим полукруг F с центром О и радиусом R (рис. 194, а ). При вращении полукруга F вокруг прямой, содержащей его диаметр NS, образуется некоторое тело F 1 (рис. 194, б ). Так как вращение вокруг прямой — движение и точка О принадлежит оси l вращения, то каждая точка тела F 1 удалена от точки O на расстояние, не большее R (движение сохраняет расстояния между точками). Это означает, что тело F 1 есть шар с центром О и радиусом R. Кроме того, при вращении границы полукруга — полуокружности — вокруг прямой l образуется сфера. Прямая, содержащая любой диаметр шара, может быть рассмотрена как ось вращения. Следовательно, сечением шара плоскостью, перпендикулярной его оси вращения l и пересекающей шар, является круг, а сечением сферы такой плоскостью — окружность этого круга; центр круга (окружности) есть точка пересечения секущей плоскости с осью l.

Плоскость, проходящая через центр шара (сферы), называется диаметральной плоскостью шара ( сферы ) . Сечением шара диаметральной плоскостью является круг, радиус которого равен радиусу шара. Такой круг называется большим кругом, а его окружность — большой окружностью ; большая окружность является пересечением сферы и её диаметральной плоскости.

19.2. Изображение сферы

Рассмотрим сферу, диаметр NS которой проведён вертикально (рис. 195, а ). Большая окружность, по которой сферу пересекает диаметральная плоскость, перпендикулярная диаметру (оси) NS, называется экватором , а точки N и S — полюсами сферы . Окружность, ограничивающая круг — изображение сферы, — называется абрисом или очерковой линией .

Типичная ошибка (!) при изображении сферы (рис. 195, б ) в том, что, изображая её экватор эллипсом, полюсы изображают расположенными на абрисе.

Для верного и наглядного изображения сферы вспомним, как в курсе черчения изображают фигуру на комплексном двухкартинном чертеже (эпюре) посредством ортогонального её проектирования на две взаимно перпендикулярные плоскости, одну из которых называют фронтальной (обозначают V ) , а другую — профильной (обозначают W ) плоскостями проекций.

Сферу расположим так, чтобы её ось N ′ S ′ была параллельна профильной ( W ), но не параллельна фронтальной ( V ) плоскостям проекций. Тогда ортогональные проекции сферы на плоскости V и W имеют вид, изображённый на рисунке 196. На нём: равные круги — проекции сферы на плоскости V и W ; отрезки A 1 B 1 и N 1 S 1 — профильные проекции соответственно экватора и оси сферы; точки N, S — фронтальные проекции полюсов (строятся с помощью линий связи); точки А, В — фронтальные проекции концов диаметра экватора, параллельного фронтальной плоскости (строятся с помощью линий связи); отрезок CD — фронтальная проекция диаметра C ′ D ′ сферы, перпендикулярного профильной плоскости; эллипс с осями АВ и CD — фронтальная проекция экватора. При таком расположении относительно плоскостей проекций сфера изображается так, как показано на рисунках 195, a ; 196, a.

Обратите внимание! Полюсы N и S не лежат на абрисе, и экватор изображается эллипсом. При этом положение полюсов N и S и положение вершин А и В эллипса-экватора взаимосвязаны.

Действительно, из равенства △ ОBF = △ ЕNО (см. рис. 196, а ) следует: OВ = EN, BF = NO. Это означает: а) если изображены полюсы N и S сферы, то вершины А и В эллипса — изображения экватора определяются из равенств OВ = ОА = NE, где NE || OD ; б) если изображён экватор (т. е. дана малая ось AB эллипса-экватора), то положение полюсов N и S определяется из равенств ON = OS = BF, где BF || OD.

На рисунке 197, а — верное и наглядное изображение сферы, на рисунке 197, б — изображение сферы верное (почему?), но не наглядное; на рисунке 197, в — неверное изображение (почему?).

 ЗАДАЧА (3.106). Найти в пространстве множество вершин всех прямых углов, опирающихся на данный отрезок АВ.

Решени е. Если ∠ АМВ = 90 ° , то точка М принадлежит окружности с диаметром АВ (рис. 198, a ).

Проведём произвольную плоскость α , содержащую отрезок АВ. В этой плоскости множество всех точек М, из которых отрезок AB виден под прямым углом, есть окружность, для которой отрезок AB — диаметр. Точки А и В этому множеству точек не принадлежат. (Почему?) Таким образом, искомое множество вершин прямых углов, опирающихся на отрезок AB , есть сфера с диаметром AB . Точки А и В этому множеству точек-вершин не принадлежат.

19.3. Уравнение сферы

Составим уравнение сферы с центром А ( a ; b ; с ) и радиусом R в декартовой прямоугольной системе координат Oxyz.

Пусть М ( x ; у ; z ) — любая точка этой сферы (рис. 199). Тогда MA = R или MA 2 = R 2 . Учитывая, что MA 2 = ( x – a ) 2 + ( у – b ) 2 + ( z – c ) 2 , получаем искомое уравнение cферы

( x – a ) 2 + ( у – b ) 2 + ( z – c ) 2 = R 2 .

Если начало системы координат совпадает с центром A сферы, то a = b = c = 0 , а сфера в такой системе координат имеет уравнение

x 2 + y 2 + z 2 = R 2 .

Из полученных уравнений следует, что сфера — поверхность второго порядка.

Так как для любой точки М ( х ; у ; z ) шара с центром А ( a ; b ; с ) и радиусом R выполняется МА ⩽ R, то этот шар может быть задан неравенством

( x – a ) 2 + ( у – b ) 2 + ( z – c ) 2 ⩽ R 2 .

При этом для всех внутренних точек М шара выполняется условие МА 2 R 2 , т. е.

( х – a ) 2 + ( у – b ) 2 + ( z – c ) 2 R 2 ,

для точек М шаровой поверхности — условие

т. е. ( х – a ) 2 + ( у – b ) 2 + ( z – c ) 2 = R 2 ,

для точек М вне шара — условие

т. е. ( х – a ) 2 + ( у – b ) 2 + ( z – c ) 2 > R 2 .

19.4. Пересечение шара и сферы с плоскостью

Рассмотрим подробнее вопрос о пересечении шара и сферы с плоскостью. Имеет место следующая теорема.

Теорема 30 (о пересечении шара и сферы с плоскостью ) . 1) Если расстояние от центра шара до данной плоскости меньше радиуса шара, то пересечением шара с плоскостью является круг. Центром этого круга является основание перпендикуляра, проведённого из центра шара на плоскость, или сам центр шара, если плоскость проходит через этот центр. Пересечением сферы с плоскостью является окружность указанного круга. Радиус r сечения в этом случае равен r = , где R — радиус шара, a d — расстояние от центра шара до плоскости сечения. 2) Если расстояние от центра шара до данной плоскости равно радиусу шара, то плоскость имеет с шаром и ограничивающей его сферой только одну общую точку. 3) Если расстояние от центра шара до данной плоскости больше радиуса, то плоскость не имеет с шаром общих точек.

Доказательств о. Пусть точка О — центр шара, R — его радиус; α — данная плоскость, точка A — основание перпендикуляра, проведённого из центра O на плоскость α . Обозначим ρ ( О ; α ) = | ОА | = d — расстояние от центра шара до плоскости α .

Рассмотрим каждый из случаев взаимного расположения шара и данной плоскости α .

1) ρ ( O ; α ) = d R и плоскость α не проходит через центр О шара (рис. 200). Докажем, что пересечение шара и плоскости есть круг с центром А и радиусом r = . Для этого достаточно убедиться, что любая точка пересечения шара и плоскости α есть точка круга с центром А и радиусом r = и, обратно, любая точка этого круга есть точка указанного пересечения.

Действительно, пусть М — произвольная точка шара, принадлежащая плоскости α (см. рис. 200). В прямоугольном треугольнике AOM по теореме Пифагора ОM 2 = ОА 2 + АМ 2 , откуда AM = . Так как точка М принадлежит шару, то ОМ ⩽ R, тогда OM 2 – OA 2 ⩽ R 2 – d 2 , поэтому АМ ⩽ . Это означает, что точка М сечения шара плоскостью α находится от точки А на расстоянии, не большем , следовательно, она принадлежит кругу с центром А и радиусом .

Обратно, пусть М — произвольная точка плоскости α , принадлежащая кругу с центром А и радиусом r = . В прямоугольном треугольнике AOM по теореме Пифагора OM 2 = ОA 2 + AM 2 . Так как AM ⩽ r , то OM 2 ⩽ OA 2 + r 2 = d 2 + R 2 – d 2 = R 2 , откуда OM ⩽ R . Значит, точка М принадлежит данному шару. Учитывая, что точка М принадлежит и плоскости α , приходим к выводу: точка M принадлежит пересечению данного шара и плоскости α .

Если неравенства, которые использовались в предыдущем доказательстве, заменить равенствами, то, рассуждая аналогично, можно доказать, что при d R пересечением сферы и плоскости является окружность с центром А и радиусом r = . Проделайте это самостоятельно.

Если плоскость α проходит через центр O шара, то d = 0, значит, r = R, т. е. сечением шара такой плоскостью является большой круг, а сечением сферы — большая окружность (см. рис. 200).

2) ρ ( O ; α ) = d = OA = R (рис. 201).

Так как ОА = ρ ( O ; α ) = R, то точка А, являющаяся основанием перпендикуляра из центра О шара на плоскость α , принадлежит шаровой поверхности, ограничивающей данный шар.

Пусть M — произвольная точка плоскости α , отличная от точки A (см. рис. 201). Тогда длины наклонной ОМ и перпендикуляра OA, проведённых из точки О к плоскости α , удовлетворяют неравенству OM > ОА = R. Значит, точка М не принадлежит шару. Следовательно, плоскость α имеет только одну общую точку с шаром — точку А.

3) ρ ( О ; α ) = ОА = d > R (рис. 202). Для любой точки М плоскости α выполняется (почему?) ОМ ⩾ d > R. Это означает, что на плоскости α нет точек шара. Теорема доказана. ▼

 ЗАДАЧА (3.161). Через середину радиуса шара проведена перпендикулярная к нему плоскость. Радиус шара равен R. Найти: а) площадь получившегося сечения; б) площади боковой и полной поверхностей конуса, основанием которого служит получившееся сечение шара, а вершиной — центр шара; в) площади боковой и полной поверхностей правильной треугольной пирамиды, вписанной в этот конус.

Решени е. а) Пусть точка O — центр шара, OD — его радиус, точка С — середина радиуса OD ; α — секущая плоскость, проходящая через точку С перпендикулярно OD.

Рассмотрим сечение шара диаметральной плоскостью, проходящей через его радиус OD. Этим сечением является большой круг с центром О и радиусом R (рис. 203); АВ — диаметр круга — сечения данного шара плоскостью α .

Так как АВ ⟂ OD и точка С — середина радиуса OD, то отрезок AB равен стороне правильного треугольника, вписанного в окружность радиуса R, значит, АВ = R , откуда

АС = r = , где r — радиус сечения шара плоскостью α . Тогда площадь этого сечения равна π r 2 = .

б) Найдём площадь поверхности конуса с вершиной О и радиусом основания r = .

Образующая ОЕ конуса (рис. 204) равна радиусу R данного шара. Поэтому площадь боковой поверхности этого конуса равна

π r • R = π • • R = ,

а площадь его полной поверхности — + = π R 2 • (2 + ).

в) Найдём площадь поверхности правильной треугольной пирамиды OEFK, вписанной в конус, радиус основания которого СK = r = , боковое ребро OE пирамиды равно радиусу R данного шара (см. рис. 204).

Так как △ ЕFK — правильный, вписанный в окружность радиуса r = , то сторона этого треугольника равна r , т. е. EF = . Тогда S △ EFK = = .

Площадь боковой поверхности пирамиды равна 3 S △ EOF = EF • ОН, где OH — апофема пирамиды. В прямоугольном треугольнике OHF находим

ОН = = = .

Тогда EF • OH = — площадь боковой поверхности пирамиды.

Следовательно, площадь полной поверхности пирамиды равна

+ = R 2 ( + ).

Ответ: a) ; б) π R 2 (2 + ); в) ; R 2 ( + ).

19.5. Плоскость, касательная к сфере и шару

Из теоремы 30 следует, что плоскость может иметь со сферой (с шаром) только одну общую точку.

Определение. Плоскость, имеющая только одну общую точку со сферой (с шаром), называется касательной плоскостью к сфере (шару), а их единственная общая точка называется точкой касания (рис. 205).

Также говорят, что плоскость касается сферы (шара) .

Любая прямая, лежащая в касательной плоскости к сфере и проходящая через точку их касания, называется касательной прямой к сфере ; эта прямая имеет со сферой единственную общую точку — точку касания, и радиус сферы, проведённый в точку касания, перпендикулярен касательной прямой.

Заметим, что если прямая a касается сферы в точке М , то эта прямая касается в точке М той окружности большого круга, которая является сечением сферы и диаметральной плоскости, проходящей через прямую a.

Справедливо и обратное: если прямая a касается окружности большого круга сферы в точке М , то эта прямая касается в точке М самой сферы.

Более того, так как прямая a, касающаяся сферы в точке М , имеет со сферой лишь одну общую точку — точку М , то эта прямая касается любой окружности, по которой пересекаются данная сфера и любая (не только диаметральная) плоскость, проходящая через прямую a. А поскольку радиус, проведённый в точку касания прямой и окружности, перпендикулярен касательной прямой, то центры всех этих окружностей — полученных сечений сферы — лежат в плоскости, проходящей через точку М перпендикулярно касательной прямой a. При этом, если точка О — центр данной сферы радиуса R , точка А — центр окружности радиуса r , по которой пересекает сферу одна (любая) из плоскостей, проходящих через касательную в точке М прямую к данной сфере, ϕ — величина угла между этой секущей плоскостью и проходящей через точку М диаметральной плоскостью данной сферы, то справедливо равенство r = R • cos ϕ ( △ ОАМ — прямоугольный, так как отрезок ОА перпендикулярен секущей плоскости (почему?)).

Для плоскости, касательной к сфере, справедливы теоремы, аналогичные теоремам о прямой, касательной к окружности на плоскости.

Теорема 31. Если плоскость касается сферы, то она перпендикулярна радиусу, проведённому в точку касания.

Доказательств о. Пусть дана сфера с центром O и радиусом R. Рассмотрим плоскость α , касающуюся данной сферы в точке M (см. рис. 205) и докажем, что ОM ⟂ α .

Предположим, что радиус ОM — не перпендикуляр, а наклонная к плоскости α . Значит, расстояние от центра сферы до плоскости α , равное длине перпендикуляра, проведённого из центра О на плоскость α , меньше радиуса. Тогда по теореме 30 плоскость α пересекает сферу по окружности. Но по условию теоремы плоскость α касается сферы и имеет с ней единственную общую точку M. Пришли к противоречию, которое и доказывает, что OM ⟂ α . Теорема доказана. ▼

Справедлива обратная теорема.

Теорема 32. Если плоскость проходит через точку сферы и перпендикулярна радиусу, проведённому в эту точку, то она касается сферы.

Доказательств о. Пусть плоскость α проходит через точку M сферы и перпендикулярна радиусу ОM (см. рис. 205). Значит, расстояние от центра сферы до плоскости равно радиусу ОM. Тогда по теореме 30 плоскость α и сфера имеют единственную общую точку M, следовательно, плоскость α касается сферы (в точке M ). Теорема доказана. ▼

Так как сечение шара плоскостью есть круг, то можно доказать, что для шара выполняются следующие метрические соотношения:

— диаметр шара, делящий его хорду пополам, перпендикулярен этой хорде;

— отрезки всех касательных прямых, проведённых к шару из одной расположенной вне шара точки, равны между собой (они образуют поверхность конуса с вершиной в данной точке, а точки касания этих прямых — окружность основания этого конуса);

— произведение длин отрезков хорд шара, проходящих через одну и ту же внутреннюю точку шара, есть величина постоянная (равная R 2 – a 2 , где R — радиус шара, a — расстояние от центра шара до данной точки);

— если из одной и той же точки вне шара проведены к нему секущая и касательная, то произведение длины отрезка всей секущей на длину отрезка её внешней части равно квадрату длины отрезка касательной (и равно a 2 – R 2 , где R — радиус шара, a — расстояние от центра шара до данной точки).

19.6. Вписанные и описанные шары и сферы

Определение. Шар называется вписанным в цилиндр, если основания и каждая образующая цилиндра касаются шара (рис. 206).

Цилиндр в таком случае называется описанным около шара. В цилиндр можно вписать шар тогда и только тогда, когда он равносторонний.

Определение. Шар называется описанным около цилиндра, если основания цилиндра служат сечениями шара (рис. 207).

Цилиндр при этом называют вписанным в шар. Около любого цилиндра можно описать шар. Центром шара служит середина оси цилиндра, а радиус шара равен радиусу круга, описанного около осевого сечения цилиндра.

Определение. Шар называется описанным около конуса, если основание конуса — сечение шара, а вершина конуса принадлежит поверхности шара (рис. 208).

Конус при этом называют вписанным в шар.

Центр шара, описанного около конуса, совпадает с центром круга, описанного около осевого сечения конуса, а радиус шара равен радиусу этого круга.

Определение. Шар называется вписанным в конус, если основание и все образующие конуса касаются шара.

Конус при этом называют описанным около шара (рис. 209). Центр вписанного в конус шара совпадает с центром круга, вписанного в осевое сечение конуса, а радиус шара равен радиусу этого круга.

Определение. Шар называется вписанным в многогранник, если он касается всех граней многогранника.

Многогранник в таком случае называют описанным около шара (рис. 210).

Не во всякий многогранник можно вписать шар. Например, вписать шар можно в любую треугольную или правильную пирамиду. А в прямую призму, в основании которой лежит прямоугольник, не являющийся квадратом, шар вписать нельзя.

При нахождении радиуса r вписанного в многогранник шара (если таковой существует) удобно пользоваться соотношением

V многогр = • r • S полн. поверх .

Шар называется вписанным в двугранный угол, если он касается его граней. Центр вписанного в двугранный угол шара лежит на биссекторной плоскости этого двугранного угла. При этом для радиуса r шара, вписанного в двугранный угол, величины α этого угла и расстояния m от центра шара до ребра двугранного угла справедлива формула: r = m • sin . Этой формулой часто пользуются при решении задач.

Шар называется вписанным в многогранный угол, если он касается всех граней многогранного угла. При решении задач, в которых рассматриваются вписанные в многогранный угол шары, удобно пользоваться соотношением: r = m • sin , где r — радиус шара, вписанного в многогранный угол, m — расстояние от центра шара до ребра многогранного угла, α — величина двугранного угла при этом ребре.

Если все плоские углы трёхгранного угла равны по 60 ° , то расстояние от вершины угла до центра вписанного в этот угол шара радиуса r равно 3 r ; если все плоские углы трёхгранного угла прямые, то расстояние от вершины угла до центра вписанного в этот угол шара радиуса r равно r . Эти соотношения часто используют при решении задач, в которых рассматриваются те или иные комбинации шаров с правильными тетраэдрами или прямоугольными параллелепипедами.

Определение. Шар называется описанным около многогранника, если все вершины многогранника принадлежат поверхности шара (рис. 211) . Многогранник при этом называют вписанным в шар.

Не около всякого многогранника можно описать шар. Например, около любой правильной или любой треугольной пирамиды шар описать можно, а около четырёхугольной пирамиды, в основании которой лежит ромб, не являющийся квадратом, шар описать нельзя (около ромба нельзя описать окружность). Более того, нельзя описать шар около любой наклонной призмы.

Вообще, для того чтобы около многогранника можно было описать шар, необходимо, чтобы около любой его грани можно было описать круг. При этом центр описанного шара может лежать как внутри многогранника, так и вне его или на его поверхности (даже на ребре многогранника), и проектируется в центр описанного около любой грани круга. Кроме того, перпендикуляр, опущенный из центра описанного около многогранника шара на ребро многогранника, делит это ребро (как хорду шара) пополам.

Мы уже говорили о пирамидах, все рёбра которых одинаково наклонены к основанию. Около таких пирамид всегда можно описать шар, центр которого лежит на луче, содержащем высоту пирамиды.

Высота h пирамиды, радиус R к описанного около основания пирамиды круга и радиус R описанного около этой пирамиды шара связаны соотношением:

( R – h ) 2 + = R 2 .

Приведём формулы для вычисления радиусов вписанных и описанных шаров для правильных многогранников с ребром a.

В задачах иногда ещё рассматривают шары, касающиеся всех рёбер данного многогранника. Для куба, например, такой шар существует и его радиус равен , где a — ребро куба.

19.7. Площади поверхностей шара и его частей

Часть шара, заключённая между секущей плоскостью и одной из двух частей его сферической поверхности, называется шаровым сегментом (рис. 212 и 214). Поверхность шарового сегмента называется сегментной поверхностью : она представляет собой часть шаровой поверхности, отсекаемую какой-нибудь плоскостью. Круг АВ, по которому плоскость пересекает шар, называется основанием шарового сегмента, а окружность этого круга — основанием сегментной поверхности. Отрезок ОС радиуса, перпендикулярного секущей плоскости, называется высотой шарового сегмента ( сегментной поверхности ) .

Часть шара, заключённая между двумя параллельными секущими плоскостями, называется шаровым слоем (см. рис. 212, 214). Поверхность шарового слоя называется шаровым поясом. Шаровой пояс — часть шаровой поверхности, заключённая между двумя параллельными секущими плоскостями. Перпендикуляр, проведённый из точки одного основания к плоскости другого, называется высотой шарового слоя ( шарового пояса ).

Сегментную поверхность и шаровой пояс можно рассматривать как поверхности вращения: в то время, как при вращении полуокружности CAA 1 D (см. рис. 212) вокруг диаметра CD образуется шаровая поверхность (сфера), при вращении дуги СА этой полуокружности вокруг того же диаметра образуется сегментная поверхность, а при вращении дуги AA 1 — шаровой пояс.

Тело, образованное при вращении кругового сектора с углом ϕ ( ϕ ° ) вокруг прямой, которая содержит диаметр круга, не имеющий с круговым сектором общих внутренних точек, называется шаровым сектором .

Из этого определения следует, что поверхность шарового сектора состоит из сегментной поверхности и боковой поверхности конуса (рис. 213, а , б ) или из поверхности шарового пояса и боковых поверхностей двух конусов (рис. 213, в, г ).

На рисунке 214 изображены различные элементы шара и сферы (шаровой сектор имеет простейший вид).

Рассмотрим вопрос о вычислении площадей сферы, сегментной поверхности, шарового пояса и шарового сектора.

а) Площадь сферы. Пусть ABCDEF — правильная ломаная линия, вписанная в данную полуокружность; a — длина её апофемы (рис. 215). При вращении полуокружности вокруг её диаметра AF образуется сфера, а при вращении ломаной ABCDEF вокруг этого же диаметра AF образуется некоторая поверхность Ф .

За площадь сферы, образованной вращением полуокружности вокруг её диаметра, принимают предел, к которому стремится площадь поверхности Ф, образованной вращением вокруг того же диаметра правильной n- звенной ломаной линии, вписанной в полуокружность, при n → + ∞ ( число сторон неограниченно возрастает ).

Поверхность Ф является объединением поверхностей, образованных вращением звеньев ломаной линии, вписанной в полуокружность, вокруг её диаметра. Этими поверхностями являются боковые поверхности либо конуса (для первого и последнего звеньев ломаной), либо цилиндра (для звеньев, параллельных оси вращения; их может и не быть), либо усечённого конуса (для всех остальных звеньев ломаной).

При вычислении площадей получившихся поверхностей воспользуемся следствиями из теорем 26, 27, 29. Площадь S i ( i = 1, 2, . n ) поверхности, образованной вращением любого звена, равна произведению 2 π , расстояния b i от середины звена до центра сферы и длины m i проекции этого звена на ось вращения, т. е. S i вращ = 2 π • b i • m i .

Так как ломаная — правильная, то все b i равны апофеме a n данной n- звенной ломаной, а m 1 + m 2 + m 3 + . + m n = 2 R и S 1 + S 2 + S 3 + . + S n = 4 π • a n • R . Причём a n = , где p n — периметр данной ломаной. Поскольку ограниченная переменная величина при n → + ∞ становится бесконечно малой, то при n → ∞ апофема a n стремится к радиусу R полуокружности.

Следовательно, предел площади поверхности Ф при n → ∞ равен 4 π R • R = 4 π R 2 . Этот предел и принимается за величину площади сферы радиуса R :

S сферы = 4 π R 2 .

б) Площади сегментной поверхности и шарового пояса. Если правильная ломаная вписана не в полуокружность, а в некоторую её часть, например в дугу AD (см. рис. 215), при вращении которой образуется сегментная поверхность, то рассуждения, аналогичные предыдущим, приводят к выводу:

S сегм. поверх = 2 π Rh ,

где h — высота сферического сегмента.

Если же ломаная вписана в дугу ВЕ (см. рис. 215), при вращении которой образуется шаровой пояс, то получим:

S шар. пояса = 2 π Rh ,

где h — высота шарового пояса.

Проделайте эти рассуждения самостоятельно.

в) Площадь поверхности шарового сектора. Эта площадь может быть получена как сумма площадей поверхности сферического сегмента и боковой поверхности одного конуса (см. рис. 213, а, б ) или как сумма площадей поверхности сферического слоя и боковых поверхностей двух конусов (см. рис. 213, в, г ).

Рассмотрим частный случай (см. рис. 213, а, б ). Если R — радиус сферы, h — высота шарового сегмента, то площадь боковой поверхности конуса с вершиной в центре сферы, образующей R , и радиусом основания (докажите это) равна π R , а площадь сегментной поверхности равна 2 π Rh. Значит, для площади шарового сектора справедлива формула

S шар. сект = π R (2 h + ) .

 ЗАДАЧА (3.418). Основанием треугольной пирамиды SABC является равносторонний треугольник АВС , сторона которого равна 4. Известно также, что AS = BS = , a SC = 3. Найти площадь сферы, описанной около этой пирамиды.

Решени е. Решим эту задачу двумя методами.

Первый метод ( геометрич е ски й). Пусть точка О — центр сферы, описанной около данной пирамиды; D — точка пересечения медиан правильного △ АВС ; точка Е — середина отрезка АВ (рис. 216).

Центр О сферы равноудалён от всех вершин △ АBС, поэтому принадлежит прямой, проходящей через точку D перпендикулярно плоскости АВС.

Так как точка Е — середина отрезка АВ, то SE ⟂ АВ ( AS = BS ) и СЕ ⟂ АВ ( △ АВС — правильный). Значит, по признаку перпендикулярности прямой и плоскости AB ⟂ ( CSE ) , поэтому ( CSE ) ⟂ ( ABC ) (по признаку перпендикулярности двух плоскостей). Это означает, что прямая OD, а следовательно, и точка О — центр сферы — лежат в плоскости CSE.

Точка D является центром окружности, описанной около △ АВС. (По этой окружности плоскость АВС пересекает сферу, описанную около данной пирамиды.) Если L — точка пересечения прямой СЕ и упомянутой окружности, то CL — её диаметр. Найдём длину диаметра CL.

В правильном △ AВС имеем: CE = = 2 ; CD = СЕ = . Тогда CL = 2 CD = .

Далее △ BSE ( ∠ BES = 90 ° ): SE 2 = SB 2 – BE 2 = 19 – 4 = 15 (по теореме Пифагора); △ SEC (по теореме косинусов):

cos C = = = ;

△ SLC (по теореме косинусов):

SL 2 = SC 2 + CL 2 – 2 SC • CL • cos C = ⇒ SL = .

Плоскость CSL проходит через центр О сферы, следовательно, пересекает сферу по большой окружности, которая описана около △ CSL. Значит, радиус R этой окружности равен радиусу сферы, описанной около данной пирамиды. Найдём длину радиуса R.

В треугольнике CSL имеем = 2 R. Так как в этом треугольнике cos C = , то sin C = = . Тогда R = = : = .

Находим площадь Q сферы:

Q = 4 π R 2 = 4 π • = π .

Второй метод ( коо р динатны й). Введём в пространстве декартову прямоугольную систему координат так, чтобы её начало совпадало с вершиной А данной пирамиды, направление оси абсцисс — с направлением луча АС, ось аппликат была перпендикулярна плоскости основания АВС пирамиды (рис. 217).

В этой системе координат вершины основания пирамиды имеют координаты: А (0; 0; 0), B (2; 2 ; 0), C (4; 0; 0).

Обозначив через х, у, z координаты вершины S пирамиды, найдём их из условий: AS = BS = , CS = 3 .

AS 2 = x 2 + y 2 + z 2 = 19,
ВS 2 = ( x – 2) 2 + ( y – 2 ) 2 + z 2 = 19,
C S 2 = ( x – 4) 2 + y 2 + z 2 = 9.

Решая систему уравнений

x 2 + y 2 + z 2 = 19, ( x – 2) 2 + ( y – 2 ) 2 + z 2 = 19, ( x – 4) 2 + y 2 + z 2 = 9,

находим: х = , у = , z = .

Таким образом, вершина S имеет следующие координаты:

S .

Пусть центр O сферы имеет координаты a, b, с, а её радиус равен R. Так как сфера описана около пирамиды SABC, то OA 2 = OB 2 = OC 2 = OS 2 = R 2 . Это соотношение в координатном виде равносильно системе уравнений

a 2 + b 2 + c 2 = R 2 , ( a – 2) 2 + ( b – 2 ) 2 + c 2 = R 2 , + + = R 2 , ( a – 4) 2 + b 2 + c 2 = R 2 .

Вычитая из первого уравнения четвёртое, получаем a = 2, после чего, вычитая из первого уравнения второе, получаем b = .

После вычитания третьего уравнения системы из первого её уравнения получаем:

= 0.

Подставив в это уравнение вместо a и b найденные их значения, получаем с = . Отсюда: R 2 = a 2 + b 2 + c 2 = 4 + + = . Тогда искомая площадь Q сферы равна:

Q = 4 π R 2 = π .

Ответ: π (кв. ед.).

19.8. Объёмы шара и его частей

Рассмотрим фигуру, образованную вращением равнобедренного прямоугольного треугольника с гипотенузой 2 R вокруг прямой, проходящей через вершину прямого угла параллельно гипотенузе (рис. 218, а ). Объём этой фигуры равен разности объёма цилиндра с высотой 2 R , радиусом основания R и удвоенного объёма конуса высоты R , радиуса основания R :

V = π • R 2 • 2 R – 2 • π • R 2 • R = π • R 3 . (*)

Шар радиуса R (рис. 218, б ) и образованную выше фигуру вращения расположим между двумя параллельными плоскостями, расстояние между которыми равно 2 R . Шар при этом будет касаться каждой из данных плоскостей, а фигуру вращения расположим так, чтобы её ось вращения была перпендикулярна этим плоскостям (см. рис. 218). (Плоскость, которая содержит верхнее основание цилиндра и касается сферы в точке N , на рисунке не изображена.)

Будем пересекать наши фигуры плоскостями, параллельными данным плоскостям и удалёнными от центра шара на расстояние x (0 ⩽ x ⩽ R ).

При х = 0 площади сечений обеих фигур равны π • R 2 ; при х = R площади сечений равны нулю. В остальных случаях площадь сечения шара равна π • ( ) 2 = π • ( R 2 – x 2 ), а площадь сечения другой фигуры (ею является кольцо) равна π • R 2 – π • x 2 . Следовательно, площади равноудалённых от центра шара сечений рассматриваемых фигур равны (относятся, как 1 : 1). Поэтому на основании принципа Кавальери равны и объёмы этих тел. Тогда на основании (*):

V шара = • π • R 3 ,

гдe R — радиус шара.

Для получения объёма шарового сегмента высоты h рассмотрим предыдущую ситуацию для R – h ⩽ x ⩽ R (при h R ) (рис. 218, 219). Применяя принцип Кавальери, получим: объём шарового сегмента равен разности объёма цилиндра высоты h и радиуса основания R и объёма усечённого конуса высоты h и радиусов оснований R и R – h , т. е.

V = π • h • R 2 – π • h • ( R 2 + R • ( R – h ) + ( R – h ) 2 ) =
= π • h 2 • (3 R – h ) .

При h > R объём шарового сегмента можно найти как разность объёма шара и объёма шарового сегмента высоты 2 R – h (рис. 220): V = π • R 3 – • π • (2 R – h ) 2 • (3 R – (2 R – h )) = π • h 2 (3 R – h ) , т. е. получаем ту же самую формулу. Подставляя в эту формулу h = R , получим V = π • R 2 (3 R – R ) = π • R 3 , что соответствует объёму полушара.