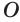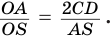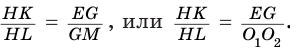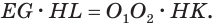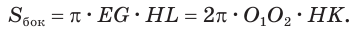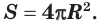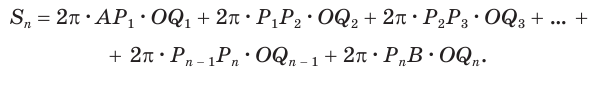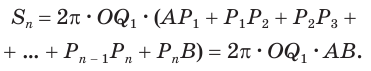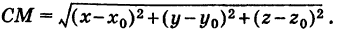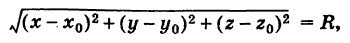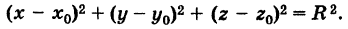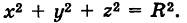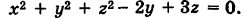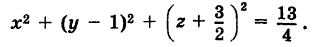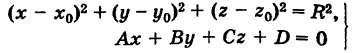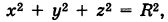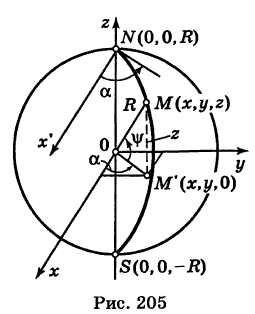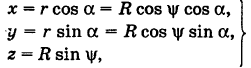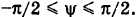Конспект урока
Геометрия, 11 класс
Урок №8. Сфера и шар
Перечень вопросов, рассматриваемых в теме:
- что такое сфера, какие у неё есть элементы (центр, радиус, диаметр сферы);
- что такое шар и его элементы;
- уравнение сферы;
- формула для нахождения площади поверхности сферы;
- взаимное расположение сферы и плоскости;
- теорема о радиусе сферы, который проведён в точку касания и теорему обратную данной.
Глоссарий по теме:
Окружность – множество точек плоскости, равноудалённых от данной точки. Данная точка называется центром окружности, расстояние от центра до любой точки окружности называется радиусом окружности.
Круг – это часть плоскости, ограниченная окружностью.
Сфера – это поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, которую называют центром.
Тело, ограниченное сферой, называется шаром.
Шар можно описать и иначе. Шаром радиуса R с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек.

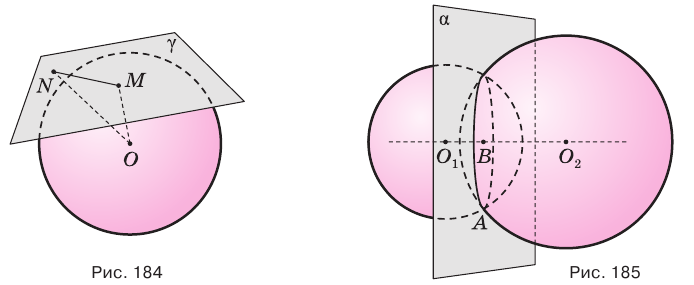
Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка – точкой касания.
Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.
Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r.
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс. 136-142.
Шарыгин И.Ф., Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений– М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 77-84.
Открытые электронные ресурсы:
Теоретический материал для самостоятельного изучения
1. Основные теоретические факты
По аналогии с окружностью сферу рассматривают как множество всех точек равноудалённых от заданной точки, но только всех точек не плоскости, а пространства.
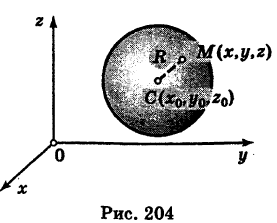
Рисунок 1 – Сфера с центром в точке О и радиусом R
Данная точка О называется центром сферы, а заданное расстояние – радиусом сферы (обозначается R). Любой отрезок, соединяющий центр и какую-нибудь точку сферы, также называется радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через центр, называется диаметром (обозначается D). D=2R.
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, которую называют центром.
Тело, ограниченное сферой, называется шаром.
Шар можно описать и иначе. Шаром радиуса R с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек.
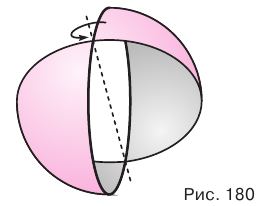
Сферу можно получить ещё одним способом — вращением полуокружности вокруг её диаметра, а шар – вращением полукруга вокруг его диаметра.
2. Уравнение сферы
Прежде чем вывести уравнение сферы введем понятие уравнения поверхности в пространстве. Для этого рассмотрим прямоугольную систему координат Oxyz и некоторую поверхность F. Уравнение с тремя переменными x, y, z называется уравнением поверхности F, если этому уравнению удовлетворяют координаты любой точки поверхности F и не удовлетворяют координаты никакой другой точки.
Пусть сфера имеет центром точку С (x0; y0; z0) и радиус R. Расстояние от любой точки М (x; y; z) до точки С вычисляется по формуле:
МС=
Исходя из понятия уравнения поверхности, следует, что если точка М лежит на данной сфере, то МС=R, или МС 2 =R 2 , то есть координаты точки М удовлетворяют уравнению:

Это выражение называют уравнением сферы радиуса R и центром С(x0; y0; z0).
3. Взаимное расположение сферы и плоскости
Взаимное расположение сферы и плоскости зависит от соотношения между радиусом сферы R и расстояния от центра сферы до плоскости d.
1. Пусть d
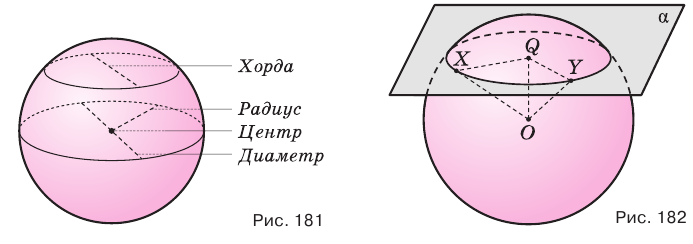
2. Пусть d=R. Если расстояние от центра сферы до плоскости равно радиусу сферы тогда сфера и плоскость имеют только одну общую точку, и в этом случае говорят, что плоскость касается сферы.
3. Пусть d
Рассмотрим случай касания более подробно.
Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка – точкой касания.
Теорема (свойство касательной плоскости).
Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
Теорема (признак касательной плоскости):
Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащей на сфере, то эта плоскость является касательной к сфере.
4. Основные формулы
Соотношение между радиусом сферы, радиусом сечения и расстоянием от центра сферы до плоскости сечения:
Формула для вычисления площади поверхности сферы и ее элементов:
S=4πR 2 – площадь сферы.
S = 2πRh – площадь поверхности сегмента сферы радиуса R с высотой h.

Примеры и разбор решения заданий тренировочного модуля
1. Площадь сечения шара, проходящего через его центр, равна 9 кв. м. Найдите площадь поверхности шара.
Площадь круга вычисляется по формуле: Sкр=πR 2 .
Площадь поверхности шара вычисляется по формуле: Sсф=4πR 2 . Радиус шара и радиуса сечения, проходящего через центр шара, одинаковые. Поэтому площадь поверхности шара в 4 раза больше площади его диаметрального сечения. То есть площадь поверхности шара равна 36.
2. Вычислите радиус круга, площадь которого равна площади сферы радиуса 5.
Площадь сферы равна Sсф=4πR 2 . То есть Sсф=100π.
По условию площадь круга некоторого радиуса r также равна 100π. Значит, r 2 =100, то есть r=10.
3. Все стороны треугольника АВС касаются сферы радиуса 5. Найти расстояние от центра сферы до плоскости треугольника, если АВ=13, ВС=14, СА=15
Окружность, вписанная в треугольник, является сечением сферы.
Найдем ее радиус.
Площадь треугольника с известными сторонами можно вычислить по формуле Герона:
С другой стороны, S=p·r.
Теперь найдем расстояние от центра шара до секущей плоскости.
4. Вершины прямоугольника лежат на сфере радиуса 10. Найти расстояние от центра сферы до плоскости прямоугольника, если его диагональ равна 16.
Так как вершины прямоугольника лежат на сфере, то окружность, описанная около прямоугольника, является сечением сферы.
Радиус окружности, описанной около прямоугольника, равен половине его диагонали, то есть r=8.
Видео:11 класс, 20 урок, Уравнение сферыСкачать

Сфера в геометрии — элементы, формулы, свойства с примерами
Сферой называется поверхность, полученная вращением окружности вокруг какого-либо ее диаметра (рис. 180). Центр этой окружности называется центром сферы.
Отрезок, соединяющий центр сферы с любой ее точкой, называется радиусом сферы, отрезок, соединяющий две точки сферы, — хордой сферы, а хорда, которой принадлежит центр сферы, — диаметром сферы (рис. 181).
Из определения сферы следует, что все ее точки равноудалены от центра сферы. Поэтому все радиусы сферы равны друг другу.
Видео:Геометрия 11 класс: Сфера и шар. Уравнение сферы. Площадь сферыСкачать

Теоремы
Теорема 1.
Сечение сферы плоскостью есть окружность, центр которой совпадает с основанием перпендикуляра, опущенного из центра сферы на секущую плоскость.
Доказательство:
Пусть сфера с центром
Пусть 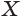
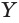
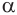
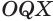
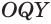
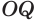
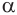
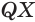
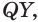
Отрезок 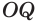
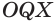
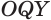
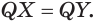
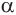


Следствие. Радиус 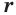
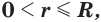
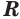
Сечение имеет наибольший радиус 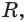
Плоскость, имеющая со сферой единственную общую точку, называется касательной плоскостью сферы. Общая точка сферы и касательной плоскости называется точкой касания.
Прямая касательной плоскости сферы, проходящая через точку касания, имеет со сферой единственную общую точку. Такая прямая называется касательной прямой сферы.
Теорема 2.
Касательная плоскость сферы перпендикулярна радиусу, проведенному в точку касания.
Доказательство:
Пусть плоскость 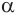
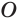

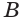
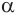

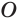

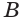
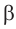
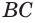

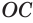
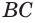
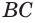

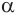
Теорема 3.
Если плоскость проходит через точку сферы и перпендикулярна радиусу, проведенному в эту точку, то она является касательной плоскостью сферы.
Доказательство:
Пусть плоскость 

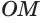
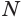


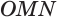
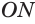
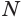





Теоремы 2 и 3 выражают соответственно свойство и признак касательной плоскости сферы.
Теорема 4.
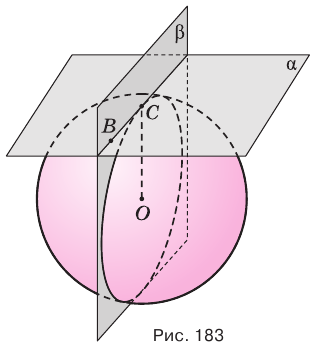
Две сферы пересекаются по окружности, плоскость которой перпендикулярна прямой, проходящей через центры сфер.
Доказательство:
Пусть имеются две пересекающиеся сферы с центрами 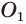
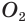
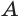
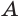
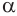
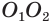
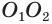

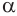


Других общих точек данные окружности не имеют. Допустим, что это не так. Пусть 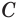

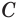
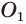
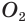
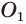
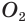

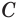
Но это противоречит утверждению о том, что две окружности имеют не более двух общих точек.
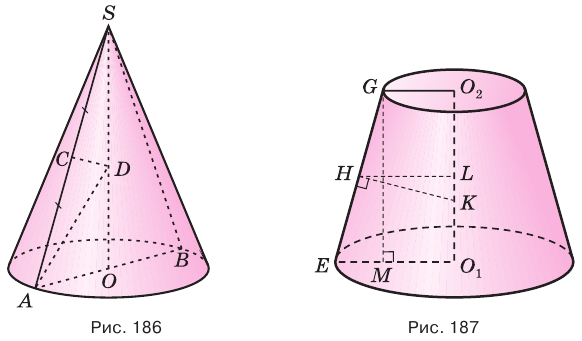
Прежде чем доказывать утверждение о поверхности сферы, обобщим утверждения о боковых поверхностях конуса, усеченного конуса и цилиндра.
Теорема 5.
Боковая поверхность конуса, усеченного конуса, цилиндра равна боковой поверхности цилиндра с той же высотой и радиусом основания, равным длине перпендикуляра, соединяющего середину образующей с точкой на оси этого тела.
Доказательство:
Пусть есть конус с вершиной 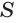
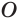
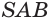
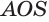
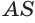
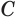
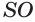
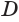
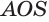
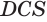
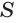
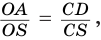
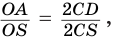
Отсюда
С учетом этого для боковой поверхности 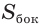
Пусть есть усеченный конус, полученный вращением прямоугольной трапеции 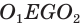
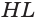
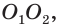
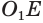
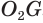
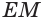
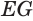
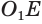
В плоскости 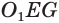
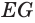
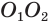
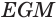
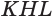
Отсюда
С учетом этого для боковой поверхности 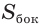
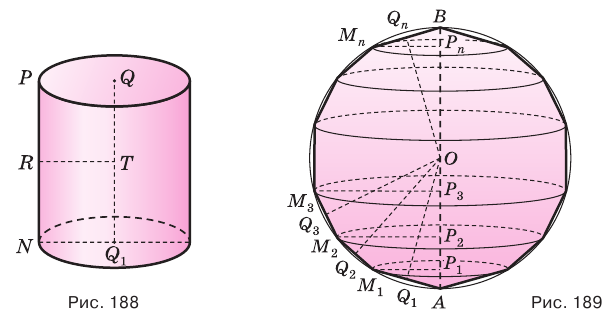
Для цилиндра утверждение очевидно (рис. 188).
Теорема 6.
Поверхность сферы равна учетверенной площади большого круга:
Доказательство:
Пусть есть сфера, образованная вращением полуокружности 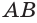
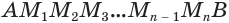
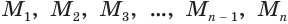
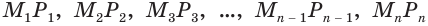
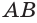


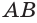
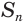
Учтем, что отрезки 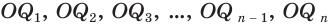
Пусть радиус сферы равен 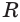
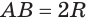
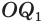
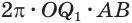
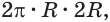
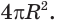
Учитывая, что 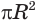
Видео:№577. Напишите уравнение сферы с центром А, проходящей через точку N, если: а) А ( — 2; 2; 0)Скачать

Уравнение сферы
Определение: Сферой радиуса R называется множество всех точек пространства, расстояние от каждой из которых до данной точки (центра) равно R.
Выведем уравнение сферы. Пусть 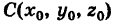
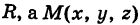
Приравнивая это выражение R, получим уравнение сферы
Если центр сферы совпадает с началом координат, то х0 = 0, у0 = 0, 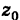
Пример:
Определить координаты центра и радиус сферы
Решение:
Объединяя члены, содержащие одноименные текущие координаты, и дополняя их до полных квадратов, будем иметь
Следовательно, центр сферы находится в точке 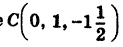
Заметим, что совокупность
уравнений сферы и плоскости определяет окружность, по которой пересекаются плоскость и сфера (если это множество не пусто). В частности, если 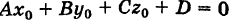
Уравнение окружности можно также писать в параметрическом виде.
Пример:
Написать параметрические уравнения меридиана сферы
проходящего через полюсы 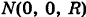
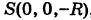
Решение:
За параметр текущей точки 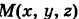
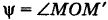
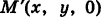
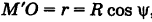
где
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Окружность
- Призма в геометрии
- Цилиндр в геометрии
- Пирамида в геометрии
- Конус в геометрии
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Геометрия 11 класс (Урок№8 - Сфера и шар.)Скачать

Урок «Сфера. Уравнение сферы»
Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Продолжаем изучение сферы.
На прошлых занятиях вы познакомились с определением сферы и шара.
Вспомним, что сферой называется поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки.
Данная точка — центр сферы.
Заданное расстояние — радиус сферы.
Прежде чем вывести уравнение сферы, познакомимся с понятием уравнения поверхности в пространстве.
Зададим прямоугольную систему координат Оxyz и некоторую поверхность F.
Уравнением поверхности F называется уравнение с тремя переменными x, y, z, если этому уравнению удовлетворяют координаты всех точек поверхности F и не удовлетворяют координаты точки, не принадлежащей этой поверхности.
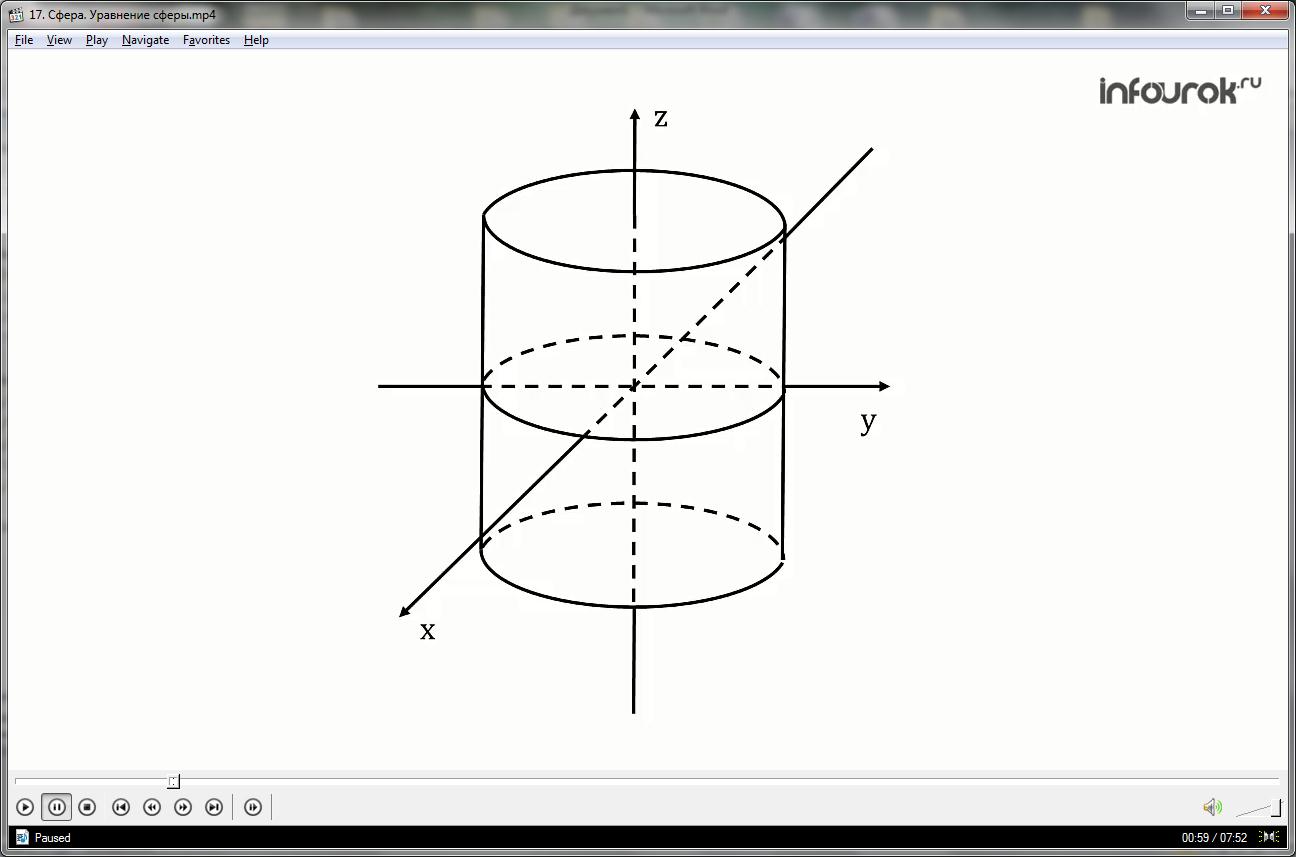
1.Рассмотрим сферу радиуса R и с центром С(x0; y0; z0).
2.Найдём расстояние от произвольной точки М(x; y; z) до центра С( x0 ; y0 ; z0) по формуле для вычисления расстояния между двумя точками с заданными координатами.
3. Если точка М лежит на сфере, то отрезок МС равен радиусу R, то есть
4.В случае если точка М не принадлежит данной сфере, то R≠МС, значит, координаты точки М не удовлетворяют уравнению R2=(x-x0)2+(y-y0)2+(z-z0)2.
5. Таким образом, в прямоугольной системе координат Оxyz уравнение сферы с центром
С (x0 ; y0 ; z0) и радиусом R имеет вид:
Применим полученные знания при решении задач.
Записать уравнение сферы с центром в точке А, которая проходит через точку N, если А(-2;2;0) и N(5;0;-1).
1.Запишем уравнение сферы с центром
А (x0 ; y0 ; z0) и радиусом R:
2.Подставим соответствующие координаты центра сферы А в данное уравнение:
Уравнение сферы с центром в точке А с координатами (-2;2;0) примет вид:
3.Так как сфера проходит через точку N с координатами (5;0;-1), то её координаты удовлетворяют уравнению сферы, подставим координаты этой точки в полученное уравнение:
Таким образом, уравнение сферы с центром в точке А, которая проходит через точку N имеет вид:
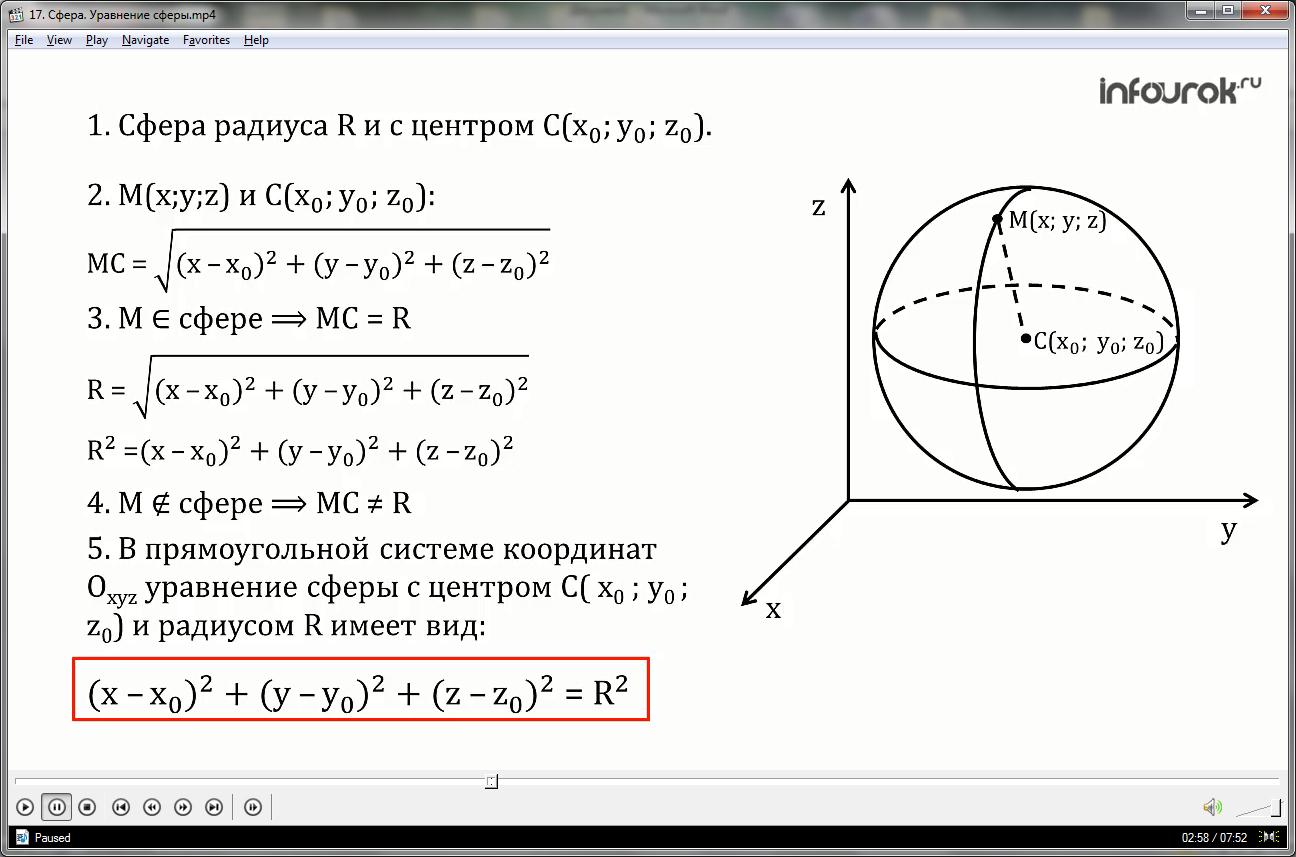
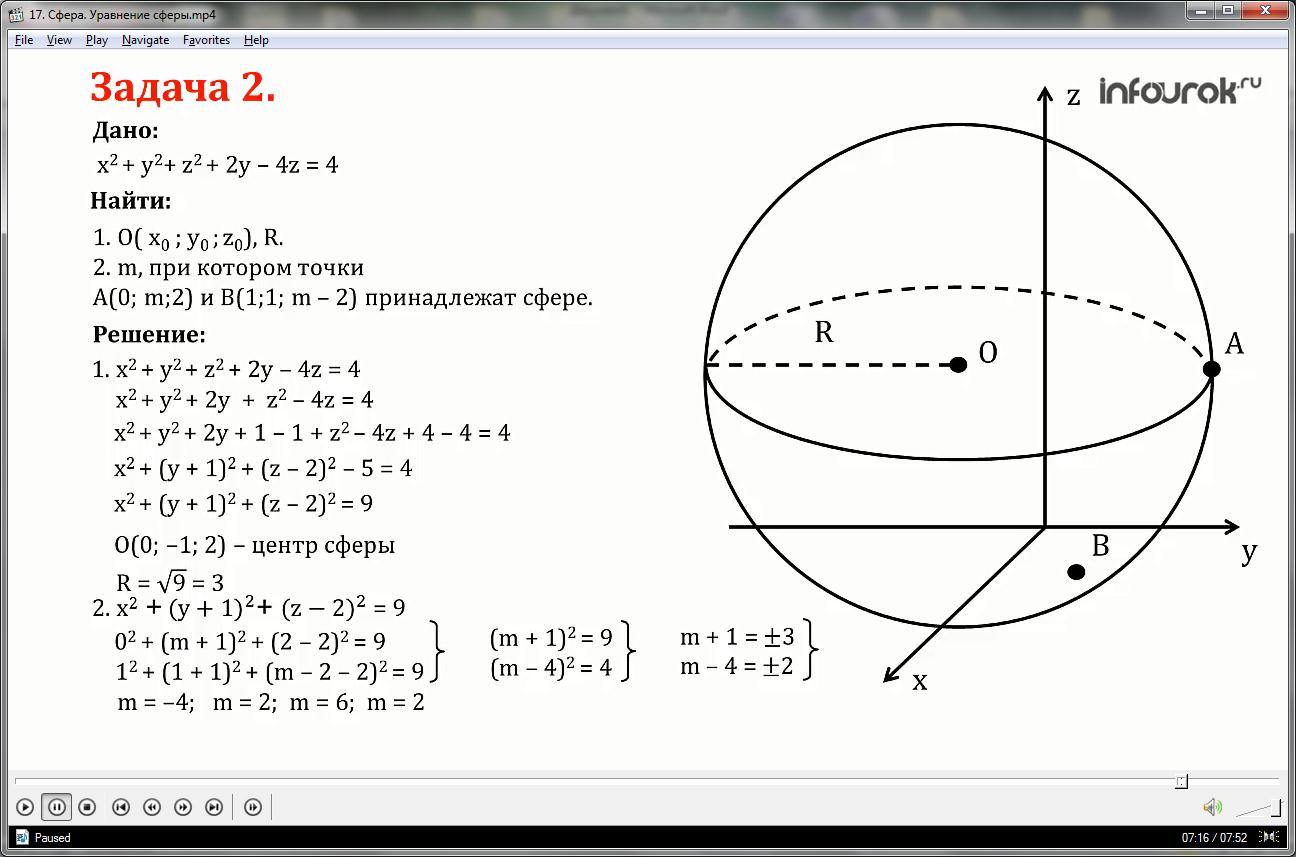
Сфера задана уравнением:
1) Найти координаты центра и радиус сферы;
2) Найти значение m, при котором точки
А (0; m;2) и В (1;1; m-2) принадлежат данной сфере.
1. Уравнение данной сферы имеет вид:
x2+ y2+ z2+2y-4z=4 или x2+ y2+2y + z2-4z=4
Выделим полный квадрат для переменных y и z, для этого прибавим и одновременно вычтем 1 и 4 в левой части уравнения:
x2+ y2+2y+1-1 + z2-4z+4-4=4
Уравнение примет вид:
x2+( y+1)2+( z-2)2-5=4 или
Таким образом, центр сферы имеет координаты:
О (0;-1;2), радиус равен R=√9=3
2.Уравнение сферы с центром в точке О (0;-1;2) и радиусом R=3 имеет вид:
Точки А (0; m;2) и В (1;1; m-2) принадлежат данной сфере, значит их координаты удовлетворяют уравнению сферы. Подставим координаты этих точек в уравнение сферы и решим систему уравнений:
Упростим полученные уравнения, раскрывая скобки и приводя подобные слагаемые:
Таким образом, мы получили 4 значения m:
Несложно проверить, что при m=-4 и m=6 координаты точек А и В не удовлетворяют уравнению сферы. Проверьте самостоятельно.
Итак, при m=2 точки А (0; m;2) и В (1;1; m-2) принадлежат сфере, заданной уравнением
x2+ y2+ z2+2y-4z=4 с центром в точке
О (0;-1;2) и радиусом R=3.
—> —>
| Инфоурок |
| 07.11.2014 |
| Геометрия |
| Видеоурок |
| 53230 |
| 1003 |
© 2022 Проект «Уроки математики»
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено!
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако команда проекта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом на электронную почту службы поддержки сайта.
🎬 Видео
№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать

УРАВНЕНИЕ ОКРУЖНОСТИСкачать

Уравнение окружности (1)Скачать

Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Уравнение плоскости. 11 класс.Скачать

11 класс, 21 урок, Взаимное расположение сферы и плоскостиСкачать

№ 621 - Геометрия 10-11 класс АтанасянСкачать

11 класс, 19 урок, Сфера и шарСкачать

11 класс, 22 урок, Касательная плоскость к сфереСкачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

11 класс, 24 урок, Взаимное расположение сферы и прямойСкачать

Урок 4 Сфера уравнение сферыСкачать

11 класс, 26 урок, Сфера, вписанная в коническую поверхностьСкачать

Уравнение касательной в точке. Практическая часть. 2ч. 10 класс.Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Шар и сфера Взаимное расположение сферы и плоскости Касательная плоскость к сфереСкачать