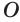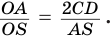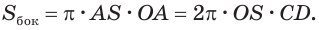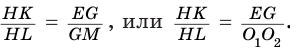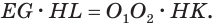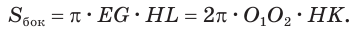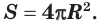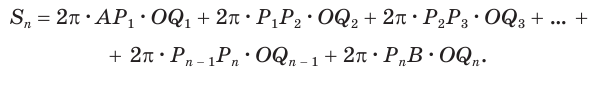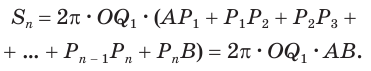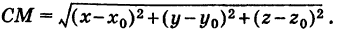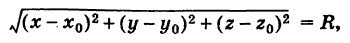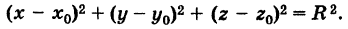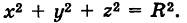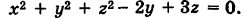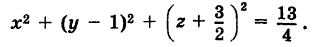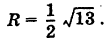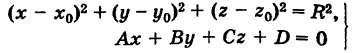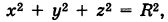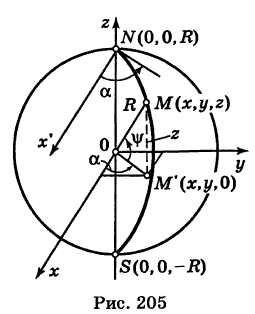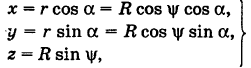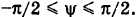Формула. Объём шара:
| V = | 4 | π R 3 = | 1 | π D 3 |
| 3 | 6 |
S = 4 π R 2 = π D 2
- Уравнение сферы
- Основные свойства сферы и шара
- Секущая, хорда, секущая плоскость сферы и их свойства
- Касательная, касательная плоскость к сфере и их свойства
- Сфера в геометрии — элементы, формулы, свойства с примерами
- Теоремы
- Уравнение сферы
- Геометрия
- Понятие сферы и шара
- Уравнение сферы
- Пересечение двух сфер
- Площадь сферы
- Вписанные и описанные сферы
- 🌟 Видео
Видео:№577. Напишите уравнение сферы с центром А, проходящей через точку N, если: а) А ( — 2; 2; 0)Скачать

Уравнение сферы
x 2 + y 2 + z 2 = R 2
( x — x 0) 2 + ( y — y 0) 2 + ( z — z 0) 2 = R 2
Видео:11 класс, 20 урок, Уравнение сферыСкачать

Основные свойства сферы и шара
Видео:Уравнение окружности (1)Скачать

Секущая, хорда, секущая плоскость сферы и их свойства
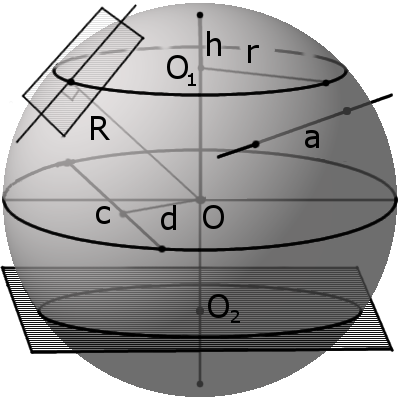
d m между секущей плоскостью и центром сферы всегда меньше радиуса R:
m r такого круга можно найти по формуле:
где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.
Видео:№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать

Касательная, касательная плоскость к сфере и их свойства
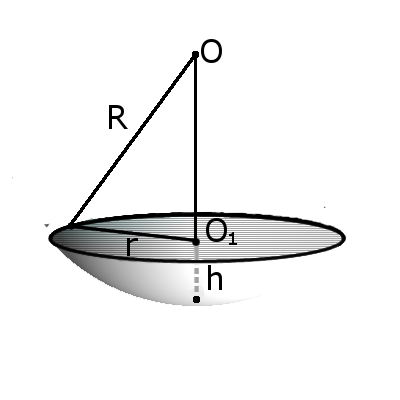
Формула. Объём сегмента сферы с высотой h через радиус сферы R:
| V = | h 2 π | (3R — h ) |
| 3 |
S = π R(2 h + √ 2 h R — h 2 )
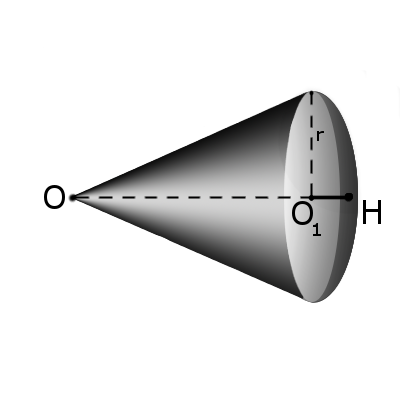
Формула. Объём сектора V с высотой O1H (h) через радиус шара OH (R):
| V = | 2 π R 2 h |
| 3 |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:№971. Напишите уравнение окружности, проходящей через точки А (-3; 0) и B (0; 9), если известноСкачать

Сфера в геометрии — элементы, формулы, свойства с примерами
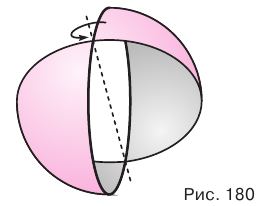
Сферой называется поверхность, полученная вращением окружности вокруг какого-либо ее диаметра (рис. 180). Центр этой окружности называется центром сферы.
Отрезок, соединяющий центр сферы с любой ее точкой, называется радиусом сферы, отрезок, соединяющий две точки сферы, — хордой сферы, а хорда, которой принадлежит центр сферы, — диаметром сферы (рис. 181).
Из определения сферы следует, что все ее точки равноудалены от центра сферы. Поэтому все радиусы сферы равны друг другу.
Видео:№970. Напишите уравнение окружности, проходящей через точку А (1; 3), если известноСкачать

Теоремы
Теорема 1.
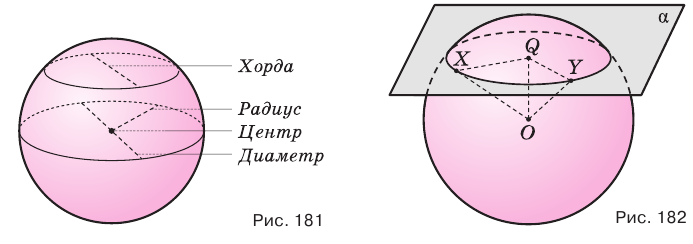
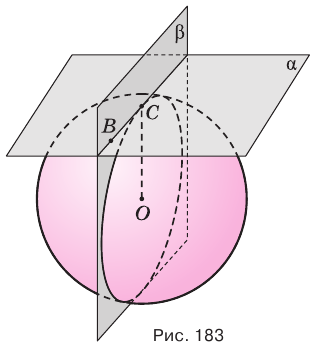
Сечение сферы плоскостью есть окружность, центр которой совпадает с основанием перпендикуляра, опущенного из центра сферы на секущую плоскость.
Доказательство:
Пусть сфера с центром
Пусть 
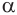
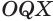
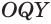
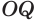
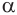
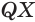
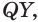
Отрезок 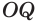
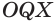
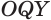
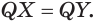
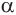


Следствие. Радиус 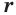
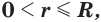
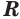
Сечение имеет наибольший радиус 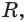
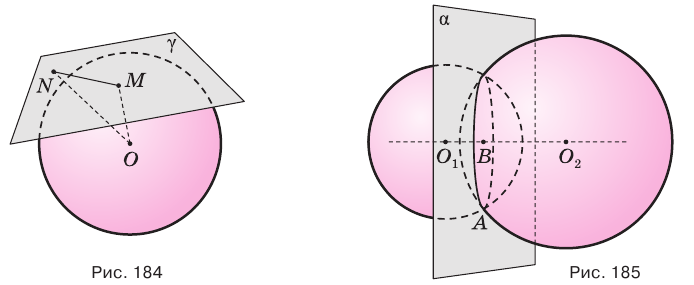
Плоскость, имеющая со сферой единственную общую точку, называется касательной плоскостью сферы. Общая точка сферы и касательной плоскости называется точкой касания.
Прямая касательной плоскости сферы, проходящая через точку касания, имеет со сферой единственную общую точку. Такая прямая называется касательной прямой сферы.
Теорема 2.
Касательная плоскость сферы перпендикулярна радиусу, проведенному в точку касания.
Доказательство:
Пусть плоскость 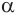
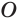

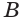
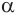

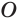

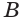
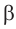
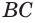

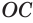
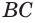
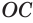
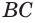

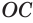
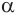
Теорема 3.
Если плоскость проходит через точку сферы и перпендикулярна радиусу, проведенному в эту точку, то она является касательной плоскостью сферы.
Доказательство:
Пусть плоскость 

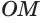
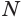


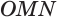
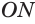
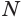





Теоремы 2 и 3 выражают соответственно свойство и признак касательной плоскости сферы.
Теорема 4.
Две сферы пересекаются по окружности, плоскость которой перпендикулярна прямой, проходящей через центры сфер.
Доказательство:
Пусть имеются две пересекающиеся сферы с центрами 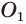
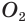
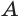
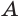
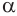
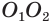
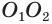

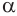


Других общих точек данные окружности не имеют. Допустим, что это не так. Пусть 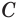

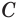
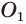
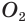
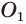
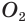

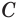
Но это противоречит утверждению о том, что две окружности имеют не более двух общих точек.
Прежде чем доказывать утверждение о поверхности сферы, обобщим утверждения о боковых поверхностях конуса, усеченного конуса и цилиндра.
Теорема 5.
Боковая поверхность конуса, усеченного конуса, цилиндра равна боковой поверхности цилиндра с той же высотой и радиусом основания, равным длине перпендикуляра, соединяющего середину образующей с точкой на оси этого тела.
Доказательство:
Пусть есть конус с вершиной 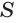
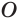
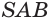
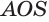
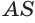
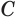
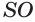
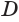
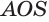
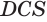
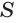
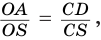
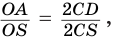
Отсюда
С учетом этого для боковой поверхности 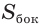
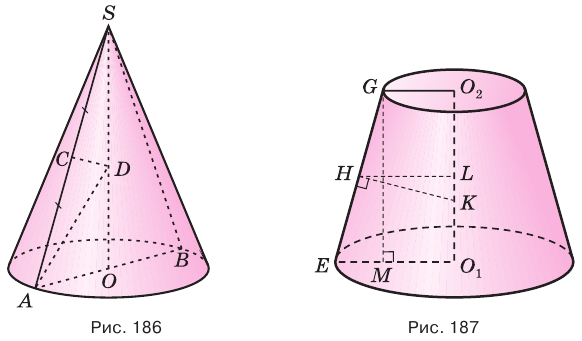
Пусть есть усеченный конус, полученный вращением прямоугольной трапеции 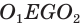
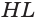
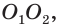
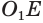
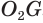
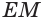
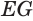
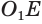
В плоскости 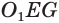
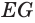
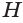
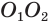
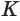
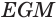
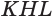
Отсюда
С учетом этого для боковой поверхности 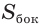
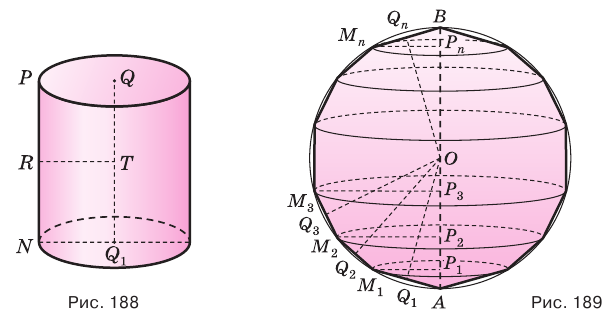
Для цилиндра утверждение очевидно (рис. 188).
Теорема 6.
Поверхность сферы равна учетверенной площади большого круга:
Доказательство:
Пусть есть сфера, образованная вращением полуокружности 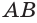
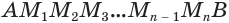
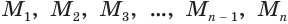
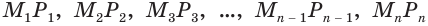
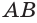


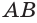
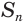
Учтем, что отрезки 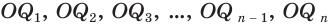
Пусть радиус сферы равен 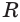
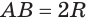
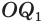
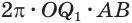
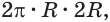
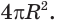
Учитывая, что 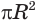
Видео:Геометрия 11 класс: Сфера и шар. Уравнение сферы. Площадь сферыСкачать

Уравнение сферы
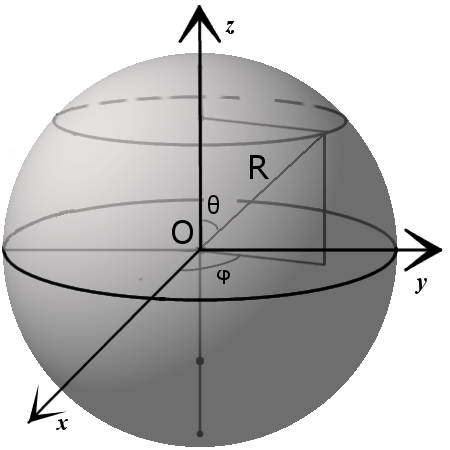
Определение: Сферой радиуса R называется множество всех точек пространства, расстояние от каждой из которых до данной точки (центра) равно R.
Выведем уравнение сферы. Пусть 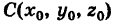
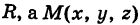
Приравнивая это выражение R, получим уравнение сферы
Если центр сферы совпадает с началом координат, то х0 = 0, у0 = 0, 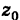
Пример:
Определить координаты центра и радиус сферы
Решение:
Объединяя члены, содержащие одноименные текущие координаты, и дополняя их до полных квадратов, будем иметь
Следовательно, центр сферы находится в точке 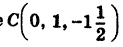
Заметим, что совокупность
уравнений сферы и плоскости определяет окружность, по которой пересекаются плоскость и сфера (если это множество не пусто). В частности, если 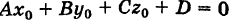
Уравнение окружности можно также писать в параметрическом виде.
Пример:
Написать параметрические уравнения меридиана сферы
проходящего через полюсы 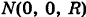
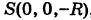
Решение:
За параметр текущей точки 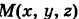
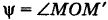
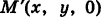
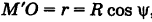
где
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Окружность
- Призма в геометрии
- Цилиндр в геометрии
- Пирамида в геометрии
- Конус в геометрии
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:№967. Напишите уравнение окружности с центром в начале координат, проходящей через точку В (-1; 3).Скачать

Геометрия
План урока:
Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Понятие сферы и шара
Люди постоянно сталкиваются с предметами, имеющими форму шара. В большинстве спортивных игр (баскетболе, большом и настольном теннисе, футболе) используются мячи, которые по форме как раз являются шарами. Такую же форму имеют многие фрукты – яблоки, апельсины, мандарины. Более того, известно, что Земля, другие планеты и звезды, большинство крупных спутников также представляют собой шары.
Важно отличать шар от сферы. Сферой называют только поверхность шара. Сам же шар является объемной фигурой, к нему относят всю часть пространства, ограниченную сферой.
Дадим строгие определения сферы и шара:
Отрезок, соединяющий точку на сфере с ее центром, именуется радиусом сферы. Он же называется и радиусом шара, заключенного внутри этой сферы.
Проходящий через центр сферы отрезок, чьи концы принадлежат сфере, именуется диаметром сферы. Сама сфера считается частью шара, также как и окружность считается частью круга.Показывают шар или сферу на рисунке так:
Из определения сферы явно вытекает тот факт, что все ее радиусы одинаковы. Это в свою очередь означает, что центр сферы – это середина диаметра, и диаметр вдвое длиннее радиуса.
Заметим, что сфера является телом вращения. Она получается при повороте полуокружности вокруг ее диаметра:
Видео:начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

Уравнение сферы
В планиметрии мы уже изучали уравнения линии. Так назывались ур-ния с двумя переменными, каждое решение которых соответствовало точке на координатной плос-ти, принадлежавшей заданной линии. Если же точка не принадлежала линии, то ее координаты решением соответствующего ур-ния не являлись. В частности, нам удалось получить уравнения прямой и окружности.
Аналогично в стереометрии вводится понятие уравнения поверхности. Так как в пространстве используются уже три координаты (х, у и z), то ур-ния поверхности содержат три переменных. Координаты всякой точки, принадлежащей поверхности, будут являться решениями ур-ния этой поверхности. И наоборот, координаты точки, не принадлежащей поверхности, будут обращать ур-ние поверхности в неверное равенство.
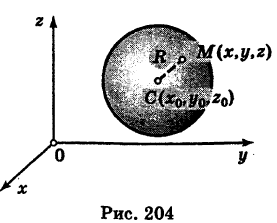
Выведем ур-ние сферы. Пусть ее центр располагается в точке С с координатами (х0, у0, z0), а радиус обозначен как R. Возьмем произвольную точку А на сфере. По определению сферы расстояние между А и С должно составлять R:
Точки, координаты которых удовлетворяют этому неравенству, находятся от центра сферы на расстоянии меньше ее радиуса. Это значит, что они находятся внутри сферы, то есть принадлежат шару, чьей поверхностью является рассматриваемая сфера. Если же координаты точки удовлетворяют неравенству
то можно утверждать, что точка находится вне пределов сферы, то есть она не принадлежит ни сфере, ни шару.
Задание. Напишите уравнение сферы, центр которой располагается в точке (2; – 4; 7) и чей радиус равен 3.
Решение. Здесь мы просто подставляем координаты центра сферы и ее радиус в ур-ние сферы:
Задание. Есть сфера с радиусом 9, чей центр располагается в точке О(2; 3; 4). Определите, какие из следующих точек будут принадлежать этой сфере: А(1; 7; – 4), В(0; 6; 10), С(– 2; – 1; 11), D(5; 6; 8).
Решение. Сначала составляем уравнение сферы, описанной в условии:
Равенство неверное, значит, В не располагается на сфере (более того, раз 49 2 .
Задание. Некоторое тело представляет собой шар, внутри которого есть полость, также имеющая форму шара, причем центры этих шаров совпадают. Докажите, что площадь сечения этого тела, проходящего через центр шаров, совпадает с площадью сечения, являющегося касательной к внутреннему шару.
Решение. Обозначим радиус большей сферы как R, а радиус меньшей (внутренней сферы) как r. Площадь центрального сечения в виде кольца (показано синим цветом) представляет собой разницу между площадью большого круга с радиусом R и малого с радиусом r:
Задание. Сфера радиусом 5 см касается каждой стороны треугольника со сторонами 13, 14 и 15 см. Каково расстояние между центром этой сферы и плос-тью треугольника?
Решение. Обозначим вершины треугольника точками А, В и С. Пусть
Заметим, что плос-ть АВС – секущая, а само сечение имеет форму окруж-ти. Эта окруж-ть будет касаться сторон ∆АВС, то есть она является вписанной окруж-тью. Как вычислить ее радиус НK?
Площадь ∆АВС можно найти по формуле Герона. Предварительно найдем полупериметр ∆АВС:
Видео:Геометрия. 10 класс. Уравнение сферы /16.03.2021/Скачать

Пересечение двух сфер
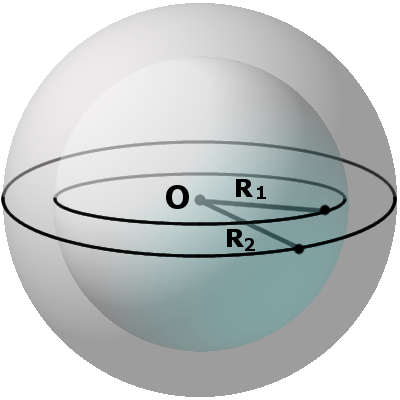
Пусть есть две пересекающиеся сферы с центрами в точках О1 и О2 с радиусами R1 и R2 соответственно. Какую форму будет иметь линия L, по которой они пересекаются?
Эта линия является множеством точек, которые принадлежат как первой, так и второй сфере. Обозначим две произвольные точки этой линии буквами А и В:
Проведем радиусы О1А, О1В, О2А и О2В. Теперь сравним ∆АО1О2 и ∆ВО1О2. Сторона О1О2 у них общая, а другие стороны попарно равны как радиусы сфер:
Получается, что ∆АО1О2 и ∆ВО1О2 равны. Теперь из точек А и В опустим высоты на прямую О1О2. Из равенства ∆АО1О2 и ∆ВО1О2 вытекает два факта:
- эти высоты упадут в одну точку Н;
- эти высоты будут одинаковы, то есть АН = НВ.
Другими словами, А и В равноудалены от Н. Получается, что точки А и В находятся на окруж-ти, центр которой – точка Н. Заметим, что О1О2 – перпендикуляр к плоскости окружности, ведь О1О2⊥АН и О1О2⊥ВН.
Точки А и В были выбраны произвольно, поэтому можно утверждать, что любые точки линии L будут находиться на одной окруж-ти. Докажем и обратное утверждение – любая точка, лежащая на этой окруж-ти, будет принадлежать линии L. Возьмем на окруж-ти какую-нибудь точку С и построим радиус НС:
Теперь сравним ∆О1НС и ∆О1НА. Они прямоугольные, ведь О1Н – перпендикуляр к плос-ти окружности. Катет О1Н у них общий, а катеты АН и НС одинаковы как радиусы окруж-ти. Значит, ∆О1НС и ∆О1НА равны, и потому
Это равенство означает, что С принадлежит сфере с центром в О1. Аналогично рассмотрев ∆О2НС и ∆О2НА, можно показать, что С также принадлежит и второй сфере. Тогда С принадлежит пересечению этих сфер.
Итак, всякая точка линии L лежит на окруж-ти с центром Н, и наоборот, каждая точка этой окруж-ти лежит на линии L. Это означает, что L как раз и является этой окружностью.
Отметим ещё один факт: по неравенству треугольника отрезок О1О2 должен быть меньше суммы отрезков О1А и О2А, то есть суммы радиусов сфер.
Задание. Сферы имеют радиусы 25 см и 29 см, а расстояние между их центрами составляет 36 см. Вычислите радиус окруж-ти, по которой они пересекаются.
Решение. Пусть А – одна их точек сечения. Искомый радиус обозначим как АН. В итоге получим такую картинку:
Видео:Уравнение окружностиСкачать

Площадь сферы
Сферическая поверхность, как и всякая другая ограниченная поверхность, имеет какую-то площадь. Напомним, что для вычисления площадей цилиндрической и конической поверхности мы строили их плоские развертки и находили площади уже этих разверток, используя формулы из планиметрии. Оказывается, что для сферы построить такую развертку невозможно. Мы не будем доказывать строго этот факт, но он известен из географии – любая карта Земли, которая как раз и должна быть разверткой сферической поверхности нашей планеты, является неточной и сильно искажает форму и размеры континентов. Если бы существовал способ построить точную развертку, то и географические карты не имели бы таких искажений.
Однако вычислить площадь сферы всё же можно по известной формуле:
Сейчас мы не будем доказывать эту формулу. Отметим лишь, что для ее получения необходимо использовать интегралы.
Задание. Какова площадь сферы с радиусом 5 см?
Решение. Просто используем формулу:
Ответ: 100π см 2 .
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Вписанные и описанные сферы
Если каждая точка многогранника лежит на поверхности сферы, то говорят, что многогранник вписан в сферу. Тогда сферу именуют описанной, а многогранник – вписанным.
Если же сфера касается каждой грани многогранника, то уже наоборот, сфера вписана в многогранник. Тогда уже сфера будет вписанной фигурой, а многогранник – описанной.
Заметим, что не в каждый многогранник может быть вписанным или описанным. Например, в куб вписать сферу можно, а в прямоугольный параллелепипед, измерения которого отличаются, уже вписать сферу не получится.
Надо отметить, что в сферу можно вписать не только в многогранник, но и другие геометрические фигуры, в частности конус и цилиндр. Здесь нужно уточнить (без доказательства), что если касание плос-ти и сферы происходит только в одной точке, то цилиндрическая и коническая поверхности касаются сферы уже по окруж-ти.
Задание. Правильная пирамида вписана в сферу. Докажите, высота этой пирамиды проходит через центр сферы.
Решение. Опустим из центра сферы О перпендикуляр ОН на основание пирамиды. Далее возьмем произвольную вершину Х основания пирамиды, и соединим ее с Н отрезком ХН. По теореме Пифагора можно вычислить длину ХН (радиус сферы ОХ обозначим, буквой R):
Получилось, что расстояние ХН не зависит от самой точки Х. То есть все вершины основания равноудалены от точки, то есть Н – центр описанной около основания окруж-ти. Это означает, что перпендикуляр ОН одновременно является высотой правильной пирамиды, ч. т. д.
Задание. Вычислите радиус описанной сферы, в которую вписан правильный тетраэдр со стороной а.
Решение. Правильный тетраэдр можно считать правильной треугольной пирамидой, поэтому (согласно предыдущей задаче) из центра сферы О можно опустить перпендикуляр на основание АВС, который упадет в точку Н – центр основания. Так как тетраэдр правильный, то ∆АВС – равносторонний, то есть Н – эта точка пересечения и медиан, и высот. Опустим из А высоту АК, она пройдет через Н. Так как АК – ещё и медиана, то
Далее найдем длину АН. Вспомним, что АН – медиана, а точка пересечения медиан Н делит их в отношении 2:1. Это значит, что
Буквой R здесь обозначен радиус описанной сферы. Осталось применить теорему Пифагора к ∆АНD:
Задание. Докажите что вокруг любого тетраэдра можно описать сферу.
Решение. Обозначим вершины произвольного тетраэдра буквами А, В, С и D. Далее на грани АВС отметим точку К – центр окруж-ти, описанной около ∆АВС. Аналогично на грани АВD отметим Н – центр окруж-ти, описанной около ∆АВD:
Напомним, что центры описанных окружностей располагаются в той точке, где пересекаются серединные перпендикуляры. Это значит, что если мы из К и Н опустим перпендикуляры на ребро АВ, то эти перпендикуляры будут серединными, то есть они попадут в одну точку М, являющуюся серединой ребра АВ.
Мы получили плос-ть НМК. Заметим, что НМК⊥АВ по признаку перпендикулярности прямой и плоскости, так как АВ⊥МН и АВ⊥МК. Но тогда АВС⊥МНК уже по признаку перпендикулярности плоскостей, ведь АВС проходит через АВ, являющийся перпендикуляром к НМК. По той же причине и АВD⊥НМК.
Далее проведем через К перпендикуляр m к АВС. Он должен будет принадлежать НМК, ведь НМК⊥АВD. Аналогично и через Н проведем перпендикуляр n к АВD, который также будет принадлежать НМК.
В плос-ти НМК есть две прямые, mи n. Они либо параллельны, либо пересекаются. Но перпендикуляры к двум плос-тям могут быть параллельны только в случае, если сами эти плос-ти параллельны (или совпадают). Но АВС и АВD непараллельны и не совпадают, поэтому m и n непаралелльны, то есть они пересекаются в какой-то точке О.
Покажем, что точка О равноудалена от всех вершин тетраэдра. Сравним ∆АОК и ∆СОК. Они прямоугольные, ведь ОК – перпендикуляр к АВС. ОК – общий катет, а катеты АК и СК одинаковы как радиусы описанной окруж-ти. Значит, ∆АОК и ∆СОК равны, ОА = ОС. Аналогично рассмотрев ∆АОК и ∆ВОК, приходим к выводу, что ОА = ОВ. Далее рассматриваем ∆ОНD и ∆ОНА и получаем, что ОА = ОD. Эти три равенства все вместе означают, что О равноудалена от точек А, В, С и D. А это значит, что на сфере с центром О и радиусом ОА будут лежать все вершины тетраэдра, то есть такая сфера окажется описанной, ч. т. д.
Примечание. Несложно доказать, что описанная сфера будет единственной. Действительно, если бы около тетраэдра можно было описать две различных сферы, то они пересекались бы в точках А, В, С и D. Сферы пересекаются по окруж-ти, то есть А, В, С и D должны лежать на одной окруж-ти, но это невозможно, ведь они не располагаются в одной плос-ти. Значит, двух описанных сфер существовать не может.
Доказанное в задаче утверждение можно сформулировать несколько иначе:
Сегодня мы изучили сферу – одну из важнейших геометрических фигур. Именно сферическую форму имеют звезды и планеты. Жидкость, оказавшаяся в невесомости, также принимает форму шара. Важно запомнить, что сечение сферы имеет форму окруж-ти, и касательные к сфере обладают почти такими ми же свойствами, как и касательные к окруж-ти в планиметрии.
🌟 Видео
№966. Напишите уравнение окружности радиуса r с центром А, если: а) А(0;5), r= 3; б) А(-1;2), r = 2Скачать

Геометрия 11 класс (Урок№8 - Сфера и шар.)Скачать

Составить уравнение окружности. Геометрия. Задачи по рисункам.Скачать

Урок 5 Уравнение сферыСкачать

№972. Напишите уравнение прямой, проходящей через две данные точки: а) А (1; -1) и В (-3; 2)Скачать

Построение окружности по трём точкам.Скачать