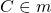Видео:№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать
Решить треугольник Онлайн по координатам
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
| A ( ; ), B ( ; ), C ( ; ) | Примечание: дробные числа записывайте Округлять до -го знака после запятой. Видео:Уравнение прямой и треугольник. Задача про высотуСкачать  Серединный перпендикуляр к отрезкуОпределение 1. Серединным перпендикуляром к отрезку называется прямая, которая проходит через середину отрезка и перпендикулярная к нему.
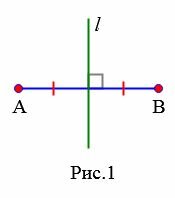
На рисунке 1 прямая ( small l ) серединный перпендикуляр к отрезку ( small AB .) Видео:Уравнения стороны треугольника и медианыСкачать  Теорема о серединном перпендикуляре к отрезкуТеорема 1. 1) Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. 2) Обратно: Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
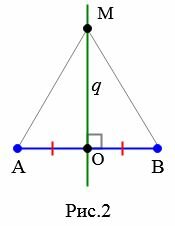
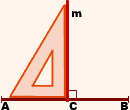
Доказательство. 1) Пусть точка ( small O ) середина отрезка ( small AB ) и пусть прямая ( small q ) серединный перпендикуляр к отрезку ( small AB ) (Рис.2). Рассмотрим любую точку ( small M ) на прямой ( small q ). Докажем, что ( small AM=BM. ) Если точка ( small M ) совпадает с точкой ( small O ), то равенство ( small AM=BM ) верно поскольку ( small AO=BO ) (( small O )-середина отрезка). Пусть ( small M ) и ( small O ) различные точки. Тогда прямоугольные треугольники ( small MOA ) и ( small MOB ) равны по двум катетам (( small AO=OB ), ( small OM )− общий). Следовательно ( small AM=BM. )
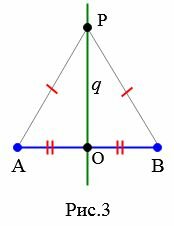
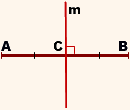
2) Пусть точка ( small P ) равноудалена от от концов отрезка ( small AB ) (Рис.3). Тогда выполено равенство ( small AP=BP ). Докажем, что ( small P ) лежит на серединном перпендикуляре ( q ). Если точка ( small P ) принадлежит прямой ( small AB ), то поскольку она равноудалена от концов отрезка ( small AB, ) она совпадает с точкой ( small O ), т.е. лежит на прямой ( q.) Если же ( small P ) не лежит на прямой ( small AB ), то треугольник ( small ABP ) равнобедренный, поскольку ( small AP=BP .) Отрезок ( small PO ) медиана этого равнобедренного треугольника и, значит, является также высотой этого треугольника. Тогда ( small PO⊥AB .) Прямые ( small PO ) и ( q ) проходят через точку ( small O ) и перпендикулярны к ( small AB .) Следовательно эти прямые совпадают, т.е. точка ( small P ) принадлежит прямой ( q. ) Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать  Серединный перпендикулярЧто такое серединный перпендикуляр к отрезку? Что можно сказать о пересечении серединных перпендикуляров к сторонам треугольника? К сторонам многоугольника? Серединный перпендикуляр к отрезку — это прямая, перпендикулярная данному отрезку и проходящая через его середину.
m — серединный перпендикуляр к отрезку AB, если точка C — середина отрезка AB,
Чтобы построить серединный перпендикуляр к данному отрезку с помощью угольника, нужно: 1) найти середину отрезка; 2) провести через эту точку прямую, перпендикулярную данному отрезку (для этого угольник прикладываем прямым углом к середине отрезка так, чтобы она сторона угольника проходила через отрезок, а через другую сторону проводим прямую):
Свойства серединного перпендикуляра. 1) Геометрическое место точек, равноудаленных от двух данных точек, есть серединный перпендикуляр к отрезку, соединяющему эти точки. Например, прямая m — геометрическое место точек, равноудаленных от точек A и B (рисунок 1).
2) Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. Эта точка является центром описанной около треугольника окружности. 3) Если около многоугольника можно описать окружность, то центр этой описанной окружности является точкой пересечения серединных перпендикуляров к сторонам многоугольника. 🎬 Видео9 класс, 7 урок, Уравнение прямойСкачать  Метод координат. Как найти медиану треугольника, если известны координаты его вершин?Скачать  Вычисляем высоту через координаты вершин 1Скачать  8 класс, 36 урок, Свойства серединного перпендикуляра к отрезкуСкачать  Геометрия 8 класс (Урок№30 - Свойство серединного перпендикуляра.)Скачать  Нахождение длины отрезка по координатамСкачать  Вычисление медианы, высоты и угла по координатам вершинСкачать  Уравнение прямой. Видеоурок 6. Геометрия 9 классСкачать  Составляем уравнение прямой по точкамСкачать  9 класс, 6 урок, Уравнение окружностиСкачать  Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать  8 класс, 37 урок, Теорема о пересечении высот треугольникаСкачать  Аналитическая геометрия на плоскости. Решение задачСкачать  Координаты середины отрезкаСкачать  УРАВНЕНИЕ ПРЯМОЙСкачать  Урок 12. Серединный перпендикуляр к отрезку (7 класс)Скачать  | |||||
