Уравнение сердечко в полярных координатах (6 видео)

Пусть математика сложит сердца

Один и один — получается два. Все одиноки — здесь ты, а там я.
Люди всегда одиноки вдвойне сами с собою наедине.
Если б их что-то сблизить могло, сразу б из двух получилось одно.
Пусть математика сложит сердца — чтобы проделать нам путь до конца.

Уильямс Джей, «Герои Ниоткуда»

Вероятно, пост следовало назвать «Как нарисовать анимированное сердечко ко дню Святого Валентина, используя математику не по назначению». Я отверг это название в пользу более поэтичного: как-никак, надвигается замечательный романтический праздник, который мы, айтишники и прочие нёрды, должны встретить во всеоружии. Я сразу покажу вам результат, а под хабракатом будет много букв о том, как я этого результата достиг.

Содержание

Дисклеймер
Шаг 1. Параметризуем сердечко.
Шаг 2. От параметрического задания к неявной функции.
Шаг 3. От неявной функции к функции двух переменных. Функция цвета.
Шаг 4. Добавляем параметр, создаём анимацию.
Замечательные кривые
Логарифмическая спираль
Кардиоида
Астроида
Строфоида
Декартов лист
Циссоида
Циклоида
Кохлеоида
Уравнения кривых. Кардиоида. Улитка Паскаля.
💡 Видео

Дисклеймер

Я осознаю, что красивое мигающее сердечко можно сделать и без малейшего знания математики. Но разве это интересно?

Шаг 1. Параметризуем сердечко.

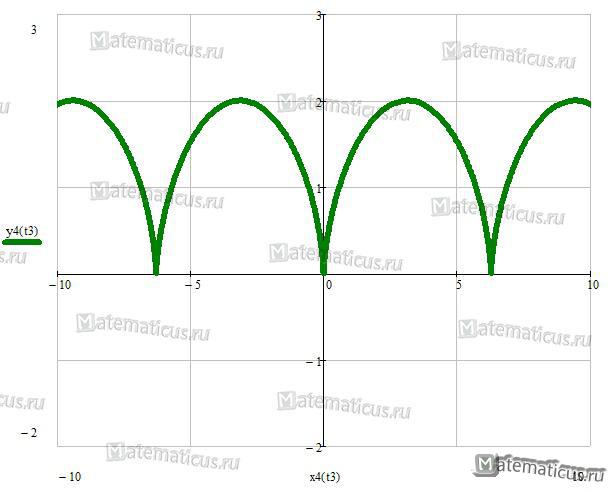
Для начала нам нужен математический объект, хотя бы отдалённо напоминающий сердечко. К счастью, для меня этот шаг был тривиален: ещё пару лет назад я обнаружил замечательную формулу как раз для такого случая (из эстетических соображений график на рисунке растянут по горизонтали, на самом деле он должен умещаться между -1 и 1).

Формула была обнаружена из следующий соображений: возьмём обыкновенную окружность и представим, что она состоит из желе, будучи при этом жёстко прикреплена к оси ординат. Теперь «подуем» на неё снизу: прибавим к координате игрек некую функцию w(x) = w(x(t)), равную нулю при x=0, монотонно возрастающую при x>0 и чётную по x. После такого «дуновения» половинки окружности сместятся вверх, образуя «выпуклости» сердечка, а благодаря жёсткому креплению к оси Y образуется нижний «хвостик» и верхняя «вмятинка». В данном случае w(x(t)) = |x| 1/2 = |cos(t)| 1/2 . Можете самостоятельно попробовать другую «функцию дуновения» и посмотреть, что из этого выйдет.

Шаг 2. От параметрического задания к неявной функции.

x = cos(t)
y = sin(t) + |cos(t)| 1/2
y — |x| 1/2 = sin(t)
(y — |x| 1/2 ) 2 + x 2 = 1
f(x,y) = (y — |x| 1/2 ) 2 + x 2 — 1 = 0

Шаг 3. От неявной функции к функции двух переменных. Функция цвета.

Имея на руках f(x,y), мы наконец можем осуществить свою мечту: нарисовать красивую цветную картинку. Для этого нам понадобится ещё одна функция: функция цвета. Она должна принимать вещественный аргумент r и возвращать целое значение от 0 до 255. Также желательно, чтобы она была монотонна на каждой полуоси и имела максимум в точке нуль. В качестве такой функции можно взять, например, эту:

Здесь 100 — «магическое число», позднее мы его в полном соответствии с «хорошим стилем программирования» заменим параметром.
Теперь для каждой точки (x,y) мы можем задать цвет как rgb(c(f(x,y)), 0, 0). Те точки, которые раньше принадлежали непосредственно графику «сердечка», стали ярко-красными (обратите внимание на неподвижный светлый контур на гифке). По мере удаления от графика цвет будет тускнеть, пока на некотором расстоянии от него не станет чёрным.

Шаг 4. Добавляем параметр, создаём анимацию.

Теперь заменим магическое число 100 параметром k. Новая функция цвета выглядит так:

Пусть k — это некоторая функция времени. Тогда для каждой точки изображения в каждый момент времени мы можем вычислить её цвет (что и является, по сути, математическим определением анимации). Сначала я хотел взять что-нибудь типа k(t) = 80(sin(t)+1). Потом, однако, я понял, что при большом количестве кадров гифка будет весить более 640 килобайт. С другой стороны, при малом количестве кадров нет смысла заморачиваться с аналитическим заданием k(t). В итоге, чтобы добиться пульсирования сердца, я последовательно присвоил k значения 80, 90, 100, 110, 120, 110, 100, 90, а затем изображения, сгенерированные для этих значений, объединил в циклический GIF. В общем-то, всё.

Видео:§30 Уравнения кривых второго порядка в полярных координатахСкачать

Замечательные кривые

Семейство роз Гранди

Уравнение имеет вид:

a — радиус лепестка;

k — положительный параметр, отвечает за количество лепестков.

Рисунок 1 — роза с тремя лепестками ρ=sin3φ

Рисунок 2 — роза с 16 лепестками ρ=sin8φ

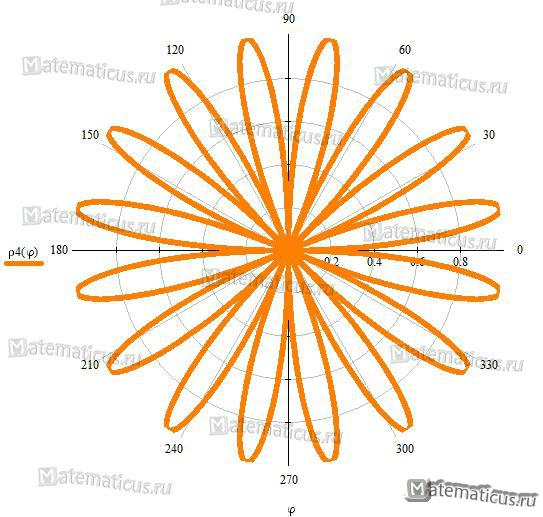
Рисунок 3 — семейство роз Гранди — напоминает ромашку ρ=sin20φ

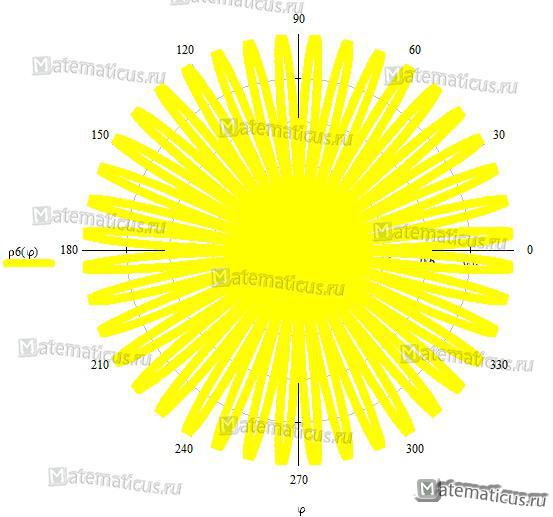
Рисунок 4 — семейство роз Гранди — линия похожа на зрачок глаза ρ=sin100φ

Видео:Построение кривой в полярной системе координатСкачать

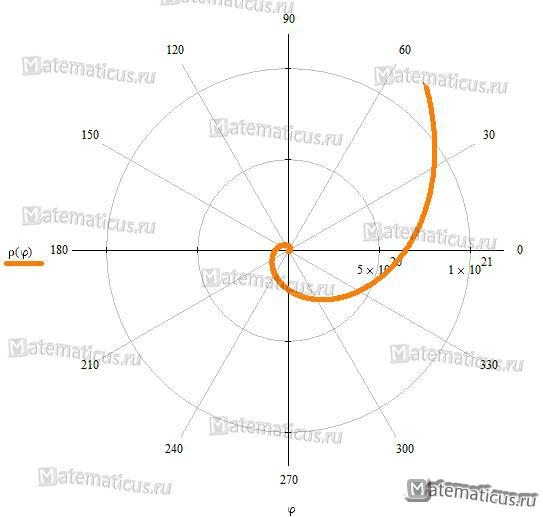
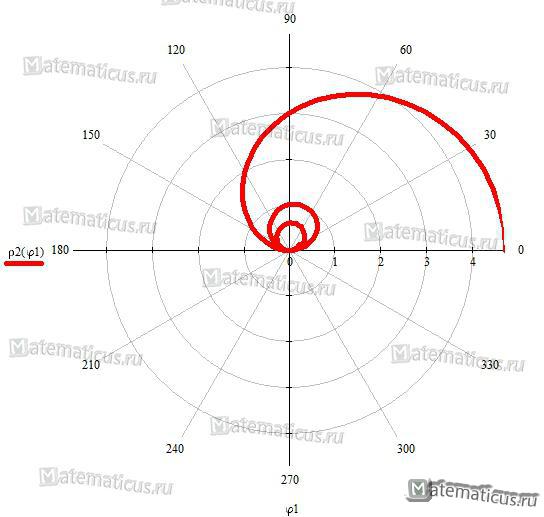
Логарифмическая спираль

Уравнение логарифмическая спираль (трансцендентная кривая) в полярных координатах:

Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

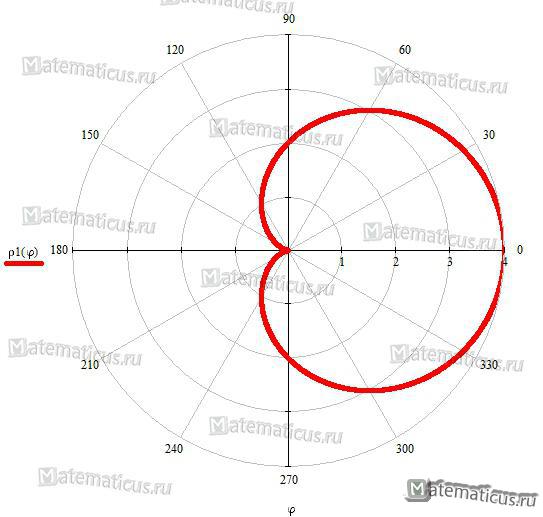
Кардиоида

Уравнение кардиоиды (перев. греч. сердце и вид) в полярных координатах:

Видео:Построение графика функции в полярных координатахСкачать

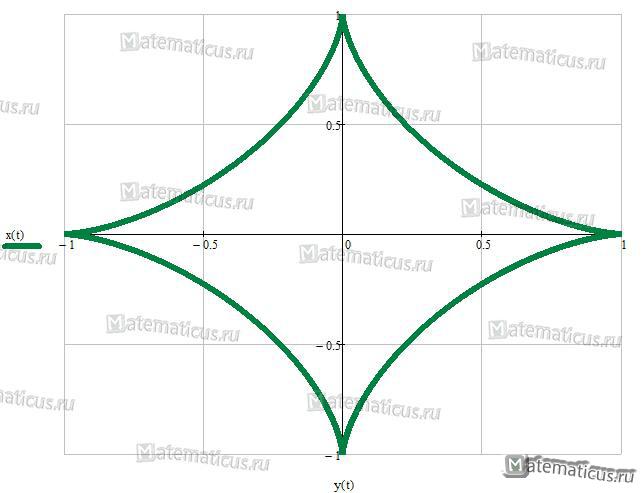
Астроида

Уравнение астроиды (перев. греч. звезда и вид) :

x 2/3 + y 2/3 = a 2/3

Видео:Полярная система координатСкачать

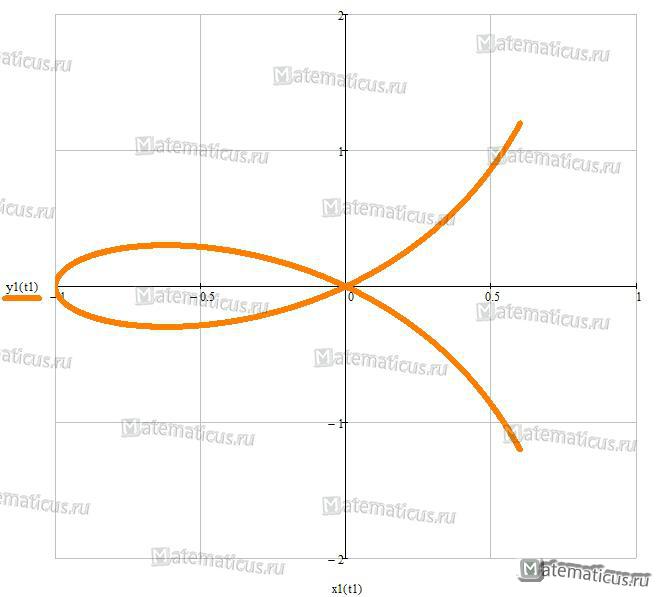
Строфоида

Уравнение строфоиды (перев. греч. крученая лента, поворот) :

y 2 (a — x)= x 2 (a + x)

Уравнение строфоиды в полярной системе координат:

Видео:Видеоурок "Полярная система координат"Скачать

Видео:Скорость и ускорение точки в полярных координатахСкачать

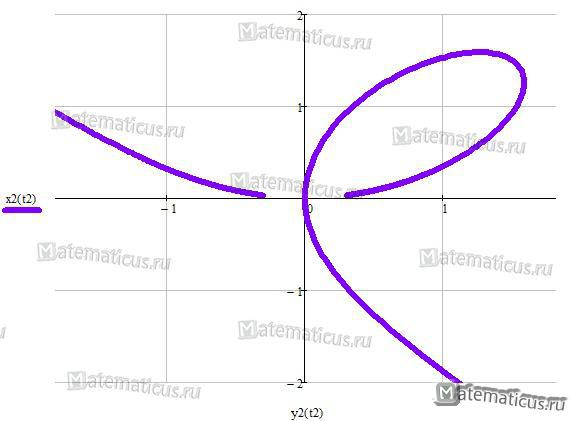
Декартов лист

Уравнение декартова листа :

x 2 + y 2 — 3axy = 0

Уравнение декартова листа в полярной системе координат:

Видео:Площадь фигуры через двойной интеграл в полярных координатахСкачать

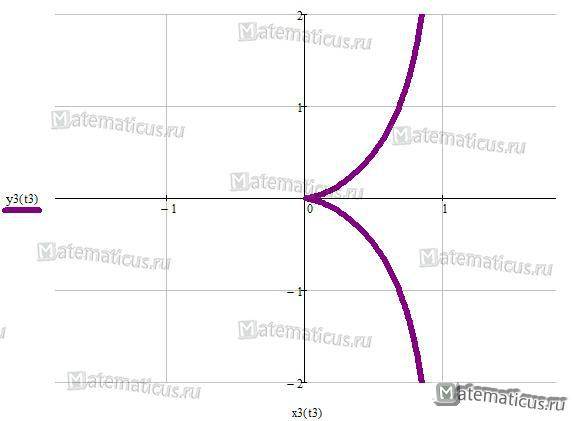
Циссоида

Уравнение циссоиды Диоклеса (перев. греч. плющ, вид) в прямоугольной системе координат :

Параметрическое уравнение циссоиды:

x = a t 2 /(1 + t 2 )

x = a t 3 /(1 + t 2 )

Уравнение циссоиды в полярной системе координат:

Видео:Лекция 22. Декартова система координат на плоскости и полярная система координатСкачать

Циклоида

Параметрическое уравнение циклоиды :

Видео:Полярная система координат.Скачать

Кохлеоида

Уравнение кохлеоиды (трансцендентная кривая) в полярных координатах:

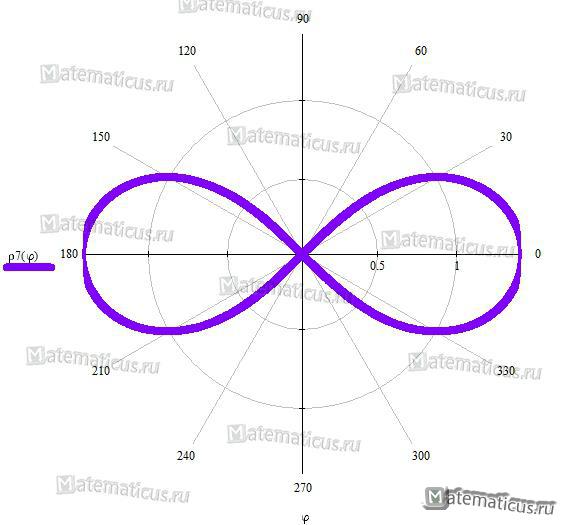
Лемниската Бернулли

Уравнение лемниската Бернулли в прямоугольных координатах:

(x 2 + y 2 ) 2 = a 2 (x 2 — y 2 )

Уравнение лемниската Бернулли в полярных координатах:

Архимедова спираль рассмотрена здесь подробно.

Применяя математические уравнения замечательных кривых, можно получить вот такие геометрические линии.

Видео:Глаза гипножабы и площадь фигур в полярной системе координатСкачать

Уравнения кривых. Кардиоида. Улитка Паскаля.

Если применить две окружности с равными радиусами и вращать одну вокруг другой, то образуется кардиоида(греч. кардиа — сердце) — математики считают, что сформированная кривая отдаленно схожа с сердцем.

Если брать точку не на самой катящейся окружности, а внутри ее, сместив в сторону от центра, тогда будет образована кривая, получившая название Улитка Паскаля или лимакона.

Пусть a – диаметр исходной окружности, а l — расстояние, на которое смещается точка вдоль радиус – вектора. Тогда возможны такие варианты улитки Паскаля: а > l, a = l и a 2 + у 2 +2аx) 2 – 4a 2 (х 2 + у 2 ) = 0;