Уравнение сен венана для газа (3 видео)

Истечение газа из резервуара через сужающееся сопло. Формула Сен-Венана-Ванцеля

Содержание

Истечение газа из резервуара через сужающееся сопло. Формула Сен-Венана-Ванцеля
Гидрогазодинамика
Р и с. 3
🔥 Видео

Видео:Уравнение состояния идеального газа. 10 класс.Скачать

Истечение газа из резервуара через сужающееся сопло. Формула Сен-Венана-Ванцеля

Истечение газа из резервуара через сужающееся сопло. Формула Сен-Венана-Ванцеля. Рассмотрим истечение газа из резервуара через узкое сопло(рис. 11.3).Размеры резервуара считаются очень большими по сравнению с размером отверстия, поэтому скорость жидкости в резервуаре можно считать равной нулю. Если конфигурация сопла выбрана правильно, распределение скорости на выходе из сопла будет приблизительно равномерным. Значения параметров газа в баке равны p0, p0 и T0.Они явно становятся тормозными параметрами. Давление во внешней среде и на выходе из сопла указано в px, а параметры газа в разделе 1-1 приведены в um, px, Tg, а площадь выхода из сопла проходит через 5. И затем… П°_ / Рэ _(Р Т ПГ РХ / По / Выражения(11.23) и (11.27）、 Или рассмотрим формулы (11.23) и (11.27)、 Последняя формула является модификацией формулы * Сен-Венана-Ванцеля о потоке газа. Определите массовый расход газа через сопло.

Адемар Жайе Клод валеду-Сен-вэн (1797-1886) выдающийся французский ученый в области машинистов и инженеров, член Парижской Академии наук. Людмила Фирмаль

Исследования по гидродинамике Сэй-Венана посвящены общим уравнениям сопротивления течению труб и каналов, гравитационным волнам, установившемуся и нестационарному движению открытых каналов, газовыделению и вязким жидкостям. Очевидно, что при постоянных p0 и p0 массовый расход изменяется так же, как и функция f (e).Эта функция исчезает с * * 0 и I = I, поэтому между этими точками существуют экстремальные значения. Найти значение e / #(e)= 0, называемое критическим. После нормального преобразования, get. In в некоторых случаях k = 1.4 e » = 0.528.It легко видеть, что найденный экстремум является максимумом. Таким образом, максимальная или критическая масса flow.

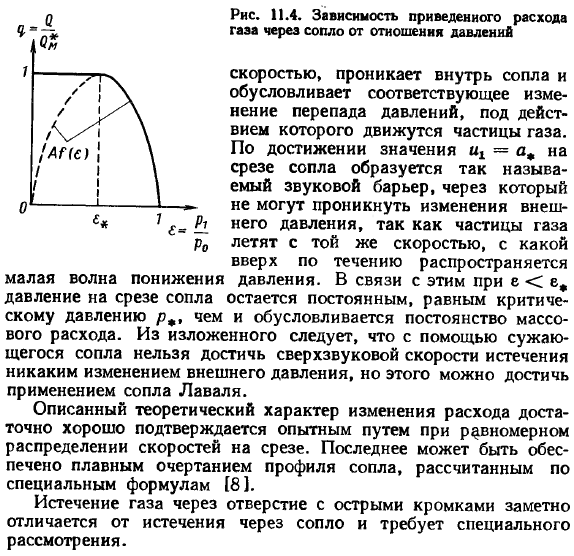
By понимая соотношение любого расхода и его критического значения С2, удобно ввести уменьшение расхода С. из формул (11.48) и (11.50) видно: уравнение (11.38) используется для представления падения расхода, вызванного падением скорости. зависимость приведенного расхода q (e) от отношения давлений e = pg / p0 четко и качественно совпадает с зависимостью f(a) (рис.11.4).Тем не менее, в 0 е е области, эта зависимость физически не реально. Это происходит потому, что поток уменьшается по мере увеличения внешнего давления px decreases. In дело в том, что из опыта фактическая зависимость 9 © следует практически из теории только в диапазоне Е, Е 1, а для е е *массовый расход остается постоянным (равным 22 (7-1)). Рис. 11.4 физическая фактическая кривая 7 (e) показана в виде твердого тела line. To найдите причину такого характера этой кривой, установите расход газа, чтобы достичь на выходе из сопла максимального расхода.

Подставляя Формулу Е формулы (11.49) в правую часть формулы (11.47), можно увидеть, что расход при x = a, то есть максимальный расход, равен скорости звука. В этом заключается причина приведенных выше характеристик зависимости 7 (е). когда давление pg уменьшается в диапазоне E1, расход естественно increases. In При достижении значения= a *на выходе из сопла образуется так называемый звуковой барьер. Это связано с тем, что частицы газа летят с той же скоростью, что и небольшие волны декомпрессии, распространяющиеся вверх по течению, поэтому изменение внешнего давления не может проникнуть through.

Кроме того, небольшое изменение внешнего давления, распространяющееся со скоростью звука, проникает через сопло и под влиянием движения частиц газа вызывает соответствующее изменение перепада давления. Людмила Фирмаль

In в связи с этим в ээ» давление на выходе из сопла поддерживается постоянным и равно критическому давлению/**.оно определяет постоянство массового расхода. Из вышеизложенного следует, что использование конусного сопла делает невозможным достижение сверхзвукового расхода за счет изменения внешнего давления, что может быть достигнуто с помощью сопла Лаваля. Описанный теоретический характер изменения расхода очень хорошо подтверждается экспериментально при равномерном распределении скорости на резании. Последнее обеспечивается плавными контурами профиля сопла, рассчитанными по специальной формуле[8]. Отток газов из острого отверстия существенно отличается от оттока из сопла и требует особого ухода.

Смотрите также:

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Видео:Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать

Гидрогазодинамика

РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ОТКРЫТЫЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ

18/6/2 Одобрено кафедрой

“Теплотехника и гидравлика

Рабочая программа и задание

с методическими указаниями

для студентов III курса

100700. ПРОМЫШЛЕННАЯ ТЕПЛОЭНЕРГЕТИКА (ПТ)

В В Е Д Е Н И Е

Предмет науки. Содержание курса и роль гидрогазодинамики в подготовке инженеров — промтеплознергетиков. Гидромеханическое представление о жидкостях как о сплошной, легкоподвижной и плохо сжимаемой среде. Газ как сжимаемая жидкость. Плотность и удельный объем, их зависимость от температуры и давления для капельных жидкостей и газов. Жидкости однородные и неоднородные . Вязкость жидкостей. Вязкость газов. Закон вязкостного трения Ньютона. Коэффициенты и единицы измерения вязкости. Зависимость вязкости от температуры и давления.

Силы, действующие в жидкости : массовые и поверхностные. Условия равновесия жидкого объема. Дифференциальные уравнения равновесия Эйлера и их интегрирование для случаев сжимаемой и несжимаемой жидкостей ; основная формула гидростатики и баро-метрическая формула. Гидростатическое давление. Закон Паскаля. Способы измерения давления. Силы гидростатического давления, действующие на плоские и криволинейные поверхности. Центр давления. Сила Архимеда. Плавание тел.

2 . ОСНОВЫ КИНЕМАТИКИ ЖИДКОСТИ И ГАЗА

Общий характер движения жидких частиц по данным наблюдений. Местная скорость. Установившееся и неустановившееся движение. Ламинарный и турбулентный режимы течения. Пульсация скорости в турбулентном потоке. Осреднение скорости по времени и по пространству.

Методы Эйлера и Лагранжа описания движения жидкости. Поле скоростей, линии и трубки тока. Уравнение сплошности течения в гидравлической и дифференциальной формах.

Ускорение жидкой частицы в переменных Эйлера. Анализ составляющих движения жидкой частицы. Теорема Коши — Гельмгольца.

Вихревое движение и основные характеристики поля вихрей Вихревая линия и вихревая трубка. Свойства вихревых трубок. Понятие о циркуляции.

Потенциальное течение жидкостей и газов. Понятие о потенциале скорости и его свойства. Суперпозиция потенциальных течений. Функция тока, ее гидродинамический смысл. Условие Коши — Римана. Комплексный потенциал. Примеры плоских потенциальных течений. Обтекание круглого цилиндра. Циркуляция . Теорема Жуковского о подъёмной силе.

Аэродинамические коэффициенты профиля.

3 . ОСНОВНЫЕ УРАВНЕНИЯ

И ТЕОРЕМЫ ДИНАМИКИ ЖИДКОСТИ И ГАЗА

Дифференциальные уравнения движения идеальной жидкости Эйлера. Переход к форме Громеки — Лэмба. Интегралы этих уравнений. Уравнение Бернулли для идеальной несжимаемой жидкости. Уравнение Сен — Венана для изотермического и адиабатического течения идеального газа. Общая форма уравнения энергии для установившегося движения сжимаемой жидкости. Общая форма уравнения количества движения жидкого объема.

Вязкая жидкость. Обобщенная гипотеза Ньютона о связи между напряжениями и скоростями деформации. Уравнения Навье — Стокса. Уравнение Бернулли для струйки вязкой жидкости.

Турбулентное движение и общие уравнения осредненно — установившегося турбулентного потока ( уравнения Рейнольдса ) . Основные гипотезы о турбулентных напряжениях.

Понятие о подобии гидромеханических процессов. Критерии подобия для течений несжимаемых вязких жидкостей и газовых течений. Понятие об автомодельности.

4 . ОДНОМЕРНЫЕ ТЕЧЕНИЯ ВЯЗКОЙ

Основные понятия и свойства одномерных течений. Плавно изменяющееся движение и закон распределения давлений по сечению. Средняя скорость и расход. Обобщение уравнения Бернулли на поток конечных размеров. Геометрическая и энергетическая интерпретация уравнения Бернулли. Напоры. Природа потерь энергии ( напора).

Классификация гидравлических сопротивлений. Коэффициенты гидравлического трения и местного сопротивления. Формулы Дарси и Вейсбаха для вычисления потерь.

Опытные данные о коэффициенте гидравлического трения. Опыты Никурадзе. Ламинарное течение в трубах. Начальный участок ламинарного течения . Формула Пуазейля. Турбулентное течение в трубах. Критическое число Рейнольдса. Элементы полуэмпирической теории турбулентного сопротивления. Гладкостенное течение : распределение скоростей и закон сопротивления. Квадратичный закон сопротивления.

Основные типы местных гидравлических сопротивлений. Потери на внезапное расширение и вход в трубу. Зависимость коэффициента местного сопротивления от числа Рейнольдса. Течения в криволинейных каналах.

Основные задачи расчета трубопроводных систем. Аналитические и графические методы расчета. Построение пьезометрических графиков. Силовое воздействие напорного потока.

Истечение несжимаемой жидкости из отверстий и насадков. Силовое воздействие свободной незатопленной струи.

5 . ОДНОМЕРНЫЕ И ДВУМЕРНЫЕ ТЕЧЕНИЯ

ИДЕ АЛЬНЫХ ГАЗОВ

Одномерные течения идеального газа. Различные формы уравнения Сен — Венана для адиабатического течения идеального газа. Энтальпия газового потока. Скорость распростра-нения звука и число М. Закономерность изменения параметров газа вдоль струйки тока. Условия непрерывного перехода через звуковое значение скорости. Критическая, максималь-ная скорости и параметры торможения. Безразмерные скорости газа. Основные газодина-мические функции, их графические представления и ислользование в расчетах.

Измерение скорости газового потока с помощью трубки Пито — Прандтля.

Истечение газа через сужающееся сопло. Формула для скорости истечения из сопла. Закономерность изменения массового расхода газа. Критическое отношение давлений. Сопло Лаваля и режимы его работы. Уравнение обращенных воздействий.

Прямой скачок уплотнения. Изменение параметров газа при переходе через скачок.

Уравнение ударной адиабаты Гюгонио, сравнение с адиабатой Пуассона. Степень сжатия газа в скачке. Рост энтропии в скачке и невозможность скачков разрежения.

6 . ГИДРОДИНАМИЧЕСКИЙ ПОГРАНИЧНЫЙ СЛОЙ.

Пограничный слой. Основные физические представления о пограничном слое. Толщина пограничного слоя и толщина вытеснения. Дифференциальные уравнения Прандтля для ламинарного пограничного слоя. Интегральное соотношение ( уравнение количества движения ) для ламинарного и турбулентного слоев. Расчет ламинарного пограничного слоя на пластинке с помощью интегрального соотношения.

Переход ламинарного погранслоя в турбулентный. Критическое число Рейнольдса и положение точки перехода на пластине. Влияние степени турбулентности внешнего потока на критическое число Рейнольдса. Пограничный слой на искривленных поверхностях. Влияние продольного градиента давления и отрыв пограничного слоя. Определение точки отрыва. Методы управления пограничным слоем.

Затопленные струи. Классификация. Свободные струи. Основные закономерности распространения свободной ламинарной струи. Струйный пограничный слой. Условия турбулизации струи. Свободная турбулентная струя . Принцип работы эжектора.

Лабораторные работы выполняют по следующим темам курса: измерение гидродина-мических величин, уравнение Бернулли и гидравлические сопротивления, истечение из отверстий, насадок и сопел, струйные течения, дозвуковой газовый эжектор.

ЗАДАНИЯ НА КОНТРОЛЬНЫЕ РАБОТЫ

Выполнению контрольных работ должно предшествовать тщательное изучение теоретических основ гидромеханики и газодинамики с привлечением специальной литературы. Каждое задание на контрольную работу состоит из десяти вариантов. Студент выполняет вариант задания, номер которого совпадает с последней цифрой учебного шифра.

При выполнении работ студент письменно отвечает на коптрольные вопросы и решает соответствующие шифру задачи. Остальные контрольные вопросы и задачи рекомендуется проработать устно.

Ответы и решения должны быть краткими, но исчерпывающими. Обязательно выполнение необходимого иллюстративного материала ( графики, силовые и скоростные многоугольники, схемы потоков и т. д. ) . Обозначения величин и терминология должны соответствовать принятым в учебниках. В конце контрольной работы необходимо привести список использованной литературы.

1. Д е й ч М. Е. , З а р я н к и н . Учебное пособие для теплотехнических специальностей вузов. М. : Энергоатомиздат , 19с.

2. А л ь т ш у л ь А. Д. и др. Гидравлика и аэродинамика . М. : Стройиздат, 19с.

3. П о в х гидромеханика. Л. : Машиностроение, 1с.

4. А б р а м о в и ч газовал динамика. М . : Наука 19с.

5. Сборник задач по машиностроительной гидравлике / Под ред. и . : Машиностроение, 19с.

6. Примеры расчетов по гидравлике / Под ред. А. Д, Альтшуля . М. : Стройиздат, 19с.

КОНТРОЛЬНАЯ РАБОТА № 1

Р а з д е л «Гидростатика и кинематика»

Ответить письменно на контрольные вопросы (см. табл.1).

1. Основные свойства жидкостей и газов.

2. Закон внутреннего трения Ньютона. Какие вы знаете коэффициенты вязкости, от каких параметров зависит их величина?

3. Дайте классификацию и определение сил, действующих в жидкости .

4. Напишите уравнение Эйлера равновесия жидкости и дайте его объяснение.

5. Чем создается и от чего зависит давление в жидкости? Пользуясь уравнением Эйлера, получите основную формулу гидростатики.

6. Дайте вывод барометрической формулы — основной формулы аэростатики.

7. Что такое поверхности равного давления? Напишите уравнение поверхности уровня давления.

8. Закон Паскаля. Принцип работы гидропресса.

9. Как определяется сила давления жидкости на стенки?

10. Что такое центр давления жидкости на стенку и где он расположен?

11. Дайте определение местной, осредненной, средней скорости , пульсации скорости, массовой скорости потока.

12. Что такое установившееся и неустановившееся движение?

13. Дайте определение ламинарного и турбулентного движения.

14. Что такое линия тока, трубка тока? Напишите уравнение линии тока. Перечислите основные свойства трубки тока.

15 . Уравнения неразрывности потока в дифференциальной и гидравлической формах.

16. Составляющие скорости жидкой частицы. Теорема Коши — Гельмгольца.

17. Каковы основные характеристики вихревого движения? Что такое вихрь, компонент вихря?

18 . Что такое вихревая линия и каково ее уравнение ? Что такое вихревая трубка и ее напряженность?

19 . Что такое циркуляция скорости и как она определяется? Изложите сущность теоремы Стокса.

20 . Какое движение называется потенциальным? Каким условиям должны удовлетворять функция потенциала скорости?

21 . Что такое функция тока и каковы ее особенности ?

22 . Дайте определения источника, стока, диполя.

23 . Сформулируйте и дайте математическое выражение теоремы импульсов.

24 . Изложите сущность теоремы .

Задача № 1. Определить плотность воздуха при давлении 5 ат и температуре 200 С.

Задача № 2 . Изменение вязкости нефтепродуктов от температуры можно представить формулой n = n 0 exp (- u t ) , где n 0 — кинематическая вязкость при t = 0 0 С. Измерениями найдено, что при t = 3 0 С n 1 = 3.6 ст, а при t = 10 0 С n 2 = 2.1 ст. Определить постоянные n 0 и u, входящие в формулу, и вычислить кинематическую вязкость при t = 6 0 С .

Задача № 3 . Автоклав объемом 10 л наполнен водой и закрыт герметически. Определить, пренебрегая изменением объема материала стенок автоклава от температуры, повышение давления в нем при увеличении температуры воды на 40 0 С. Коэффициент термического расширения воды равен 0.00018 1/град, а коэффициент объемного сжатия равен 4м2/Н.

Задача № 4 . Пользуясь формулой закона Ньютона, определить напряжение трения на стенке, обтекаемой потоком воздуха при нормальных условиях. Известно, что на расстоянии 0.5 мм от стенки величина скорости равна 19 м/с. Изменение скорости у стенки можно принять линейным.

Задача № 5 . Определить касательное напряжение трения на стенке, обтекаемой водой, если вблизи стенки изменение скорости воды по нормали к ней выражается формулой V = 516y — 13400 y 2 , где y — расстояние от стенки. Температура воды 15 0 С.

Задача № 6 . Найти избыточное Р и и абсолютное Р а давление на глубине 400 мм под свободной поверхностью ртути, если барометрическое давление эквивалентно высоте h б = 756 мм рт. ст. Выразить также барометрическое давление в МПа.

Задача № 7 . Определить высоту налива нефти в резервуаре, сообщающемся с атмосферой, если манометр, установленный на высоте 1 м выше днища резервуара, показывает давление 0.5 ати, а плотность нефти 900 кг/м3.

Задача № 8 . Для измерения падения давления в вентиляционной трубе применяется наклонный микроманометр, наполненный спиртом с удельным весом 800 кг/ м3 . Угол наклона трубки манометраОпределить необходимую длину шкалы манометра для измерения падения давления до 0.001 ат.

Задача № 9 . В печи и дымовой трубе дымовые газы имеют в среднем температуру 3000С и удельный вес 4.3 Н/м3 . Температура наружного воздуха 140С, давление 760 мм рт. ст. Высота дымовой трубы 5 м. Определить разность давлений ( тягу ) по обе стороны закрытой печной дверки, расположенной у основания.

Задача № 10. Измеритель ускорения, установленный на электровозе, представляет собой U — образную трубку , наполненную водой и расположенную в плоскости движения. Расстояние между вертикальными коленами трубки 200 мм. Определить ускорение электровоза, если при торможении разность уровней воды в трубках составила 100 мм.

Задача № 11. Цилиндрический сосуд диаметром 4 см и высотой 10 см наполнен водой до половины. С каким предельным числом оборотов можно вращать этот сосуд вокруг вертикальной оси, чтобы из него еще не выливалась вода?

Задача № 12. Для измерения высоты подъема применяют точный барометр. Перед вылетом барометр показывал давление 745 мм рт. ст. , а в наивысшей точке подъема — 500 мм рт. ст. Определить высоту подъема, считая температуру воздуха по всей высоте равной 10 0С.

Задача № 13. Подпорная прямоугольная вертикальная стенка шириной b = 200 м сдерживает напор воды высотой H = 10 м. Определить силу полного давления на стенку N и опрокидывающий момент М. Построить эпюру давлений.

Задача № 14 . Определить усилие, стремящееся разорвать полностью наполненную нефтью железнодорожную цистерну, если плотность нефти 900 кг /м3 , длина цистерны 10 м, а диаметр 3 м.

Задача № 15. Человек поднимает в обыкновенных условиях железный шар весом Gо = 300 Н. Какого веса шар может быть им поднят под водой?

Задача № 16 . Доказать, что если при вращении жидкости вокруг вертикальной оси угловая скорость частиц убывает обратно пропорционально квадрату расстояния от оси вращения, то течение потенциально. Найти потенциал скорости и функцию тока y.

Задача № 17 . Скорость частиц жидкости, совершающей вращение вокруг вертикальной оси, изменяется обратно пропорционально расстоянию от оси вращения. Найти значение циркуляции вдоль линии тока.

Задача № 18. Найти уравнение линии тока плоского потока, заданного потенциалом скоростей j = а Х Y, вычислить циркуляцию скорости Г вдоль прямоугольника произ-вольной величины, стороны которого параллельны осям координат.

Задача № 19 . Плоский установившийся поток задан проекциями скоростей на оси координат :

Vx = 2х / Ö R ; Vy = 2y / Ö R

где R = Х2+ Y2 . Найти потенциал скоростей j и уравнение линий тока.

Задача № 20 . Исследовать плоский поток и найти функцию тока, если Vx = а х2 ,

К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ № 1

Задачи № 1-5 — на основные физические свойства жидкостей и газов. В задачах № 4 и 5 необходимо применить закон внутреннего трения Ньютона, согласно которому касательное напряжение трения определяется выражением :

Производную определяют дифференциированием или заменяют отношением конечных разностей. Величину коэффициента динамической вязкости m при расчетах берут из таблиц.

Задачи № на применение основной формулы гидростатики , согласно которой абсолют-ное давление в любой точке жидкости, находящейся в равновесии в поле сил тяжести, опре-деляется как сумма давления на ее свободной поверхности P0 и избыточного гидростатичес-кого давления на соответствующей глубине :

Задачи № 10 и 11 — на равновесие жидкости при одновременном действии сил тяжести и сил инерции. Для решения задачи № 12 необходимо применить барометрическую формулу для изотермической атмосферы, согласно которой давление убывает с высотой по экспоненте :

P = P0 exp( — g h / R T)

Здесь P0 — давление атмосферы на уровне земли.

В задачах № 13 и 14 для определения силового воздействия давления жидкости на стенки используют следующие теоремы :

1. Сила суммарного избыточного гидростатического давления на плоскую стенку равна произведению величины давления на глубине центра тяжести смоченной поверхности на величину ее площади :

N = Pц. т. S = r g h ц. т. S

Точку приложения этой силы называют центром давления. Положение центра давления в плоскости стенки определяют по формуле :

l ц. д = l ц. т. + I / l ц. т. S

Здесь l ц. т. и l ц. д — расстояние от свободной поверхности жидкости до центра тяжести и центра давления, измеренное в плоскости стенки ( см. рис. 1 ) , I — момент инерции смочен-ной поверхности относительно горизонтальной оси, проходящей через центр тяжести.

2. Для криволинейной стенки суммарную силу давления принято разделять на горизонталь-ную и вертикальную компоненты. Для определения горизонтальной силы нужно спроекти-ровать криволинейную поверхность на вертикальную плоскость. Затем горизонтальную силу определяют по теореме 1 :

NX = Pц. т. Sпр = r g h ц. т. Sпр,

где h ц. т и Sпр относятся к этой проекции. Вертикальная компонента равна весу жидкости в теле давления :

Тело давления заключено между криволинейной поверхностью, свободной поверхностью жидкости и соответствующими вертикальными плоскостями. Если оно заполнено жидкостью, то силу берут со знаком плюс, если жидкости в теле давления нет — со знаком минус.

В задачах №рассматривают плоские течения несжимаемой идеальной жидкости. Для плоского течения аналитическое условие потенциальности течения принимает вид :

Для потенциала скорости j и функции тока y справедливы соотношения :

d j /dx = Vx, d j /dy = Vy ;

d y /dx = — Vy, d y /dy = Vx.

По этим соотношениям обратным интегрированием и находят функции j и y.

Уравнение линии тока на плоскости x , y находят интегрированием соответствующего дифференциального уравнения:

КОНТРОЛЬНАЯ РАБОТА № 2

Р а з д е л «Гидродинамика»

18 для все вариантов

Ответить письменно на контрольные вопросы ( см. табл. 2)

1 . Напишите дифференциальные уравнения движения идеальной жидкости Эйлера.

2. Напишите дифференциальные уравнения движения идеальной жидкости в форме Громеки — Лэмба. Каковы интегралы этих уравнений?

3 . Каковы особенности движения вязкой жидкости и в чем смысл обобщенной гипотезы Ньютона?

4. Напишите уравнения Навье — Стокса.

5 . Напишите критерии Рейнольдса, Эйлера, Фруда, Архимеда и объясните их физический смысл.

6. В чем смысл теории подобия гидродинамических процессов, сущность моделирования?

7 . Напишите и объясните уравнение Бернулли для идеальной несжимаемой жидкости. Дайте энергетическую и геометричесую интерпретацию членов уравнения.

8. Напишите уравнение Бернулли для потока реальной жидкости конечных размеров.

9 . Что такое полный и пьезометрический напоры? Как они измеряются? Что такое гидравлический уклон?

10. Дайте классификацию гидравлических сопротивлений. Напишите и объясните формулы Дарси и Вейсбаха.

11. Выведите формулу местных потерь напора при внезапном расширении трубы.

12. Изложите сущность опытов Никурадзе. Какие существуют области трения при течении жидкости по трубам?

13. Каков закон распределения скоростей при ламинарном течении жидкости в трубе круглого сечения? Формула Пуазейля.

14. Напишите и объсните формулу Стокса для силы сопротивления движению шара в вязкой жидкости.

15. В чем состоит особенность перехода ламинарного течения жидкости в турбулентное? Критическое число Рейнольдса.

16 . Каковы основные характеристики турбулентного течения? Напишите и объясните формулу Прандтля.

17. Как определяют величину коэффициента гидравлического сопротивления при турбулентном течении в трубах?

18. Основные задачи расчета трубопроводных систем. Последовательное и параллельное соединение труб.

19 . Как вычислить коэффициент расхода и расход при истечении капельных жидкостей из сосудов через отверстия и насадки?

20 . В чем состоят основные особенности неустановившегося движения жидкости в трубах?

Задача № 1 . В поток жидкости, имеющий в поперечном сечении w1 расход Q1 , вливается другой поток той же жидкости, характеризуемый расходом Q 2 . Определить живое сечение бокового притока w 2 и сечение потока после слияния , считая скорости во всех сечениях одинаковыми.

Задача № 2 . По трубопроводу диаметром d = 156 мм прокачивают мазут плотностью r = 900 кг / мЗ. Определить объёмный расход Q и скорость Vср, если массовый расход G =кг / ч.

Задача № 3 . По газопроводу диаметром d = 156 мм перекачивают газ, абсолютная вязкость которого m = 8н. с / м2 , плотность r = 1 кг / м3, массовый расход G = 0, 2 кг / с. Определить характер движения и приведенную скорость.

Задача № 4 . Определить критическую среднюю скорость, при которой движение воды по трубопроводу диаметром d = 100 мм переходит из ламинарного в турбулентное, если температура воды t = 20 ° С.

Задача № 5 . По трубе диаметром D = 200 мм течет нефть в количестве Q = 60 л / с. Определить, какое количество воды должно протекать по трубе диаметром d = 150 мм, чтобы движение в обеих трубах было гидродинамически подобным. Кинематические вязкости нефти и воды при температуре прокачки: nн = 0,14 см2/ с; n в = 0,01 см2 / с.

Задача № 6 . По горизонтальной трубе переменного сечения протекает идеальная жидкость с удельным весом g = 8 , 32 кН / м3 в количестве q = 10 л / с. Определить пьезо-метрические высоты в сечениях 1 , 2 , 3 , если d 1 = d 3 = 100 мм ; d 2 = 25 мм ; Р 1 = 0,3 МПа.

Задача № 7 . Для измерения скорости воздушного потока используется трубка Пито-Прандтля с двумя отверстиями для измерения давления : динамическим ( Р0) и статическим (Р) ( рисОпределить скорость воздушного потока, если показание дифференциального жидкостного манометра, подсоединенного к ним и залитого водой, равно 100 мм.

Задача № 8 . Расход жидкости в трубопроводе измеряют с помощью расходомера Вентури. Определить расход воды, если показание подсоединенного к нему ртутного дифференциального манометра равно 300 мм. Диаметр трубы Вентури в широкой части 60 мм, в узкой — 30 мм.

Задача № 9 . По газопроводу передается газ в количестве 6 млн. м3 / сут. По трассе расположены компрессорные станции, которые дают абсолютное давление газа на выходе Р1= 40 ата. Степень повышения давления в компрессоре 1.4 , т. е. давление Р2 на входе следующей станции должно быть равно 28.2 ата. Труба газопровода имеет диаметр 630 мм. Определить расстояние между компрессорными станциями, если нормальная плотность газа при давлении 760 мм равна 0.722 кг / м 3 . Температура газа при перекачке 20 0С. Коэффициент кинематической вязкости при этих условиях равен n = м2/c.

Задача № 10 . Требуется определить давление в начале водопровода диаметр которого 150 мм, длина 20 км, если расход составляет 1500 м3 / сут, а давление в конце трубопровода 1.5 ати. Температуру принять равной 20 0С. Найти также требуемую мощность насоса, если коэффициент полезного действия насоса 80 % .

Задача № 11 . Определить гидравлический уклон i в трубопроводе постоянного диаметра длиной L = 10 км при перекачке воды, если в начале трубы давление Р2 больше, чем давление Р в конце, на величину D P = 3000 кН / м2 , и конец трубы расположен выше начала на Z = 20 м.

Задача № 12 . Определить осевую скорость в трубе диметром d = 120 мм при ламинарном движении, если измеренная на расстоянии у = 40 мм от стенки местная скорость V = 1,51 м / с.

Задача № 13 . По прямой трубе длиной L = 1 км, диаметром d = 100 мм протекает ламинарно со средней скоростью Vср жидкость, имеющая кинематическую вязкость n = 0.4 см2 / с. Определить потерю напора на трение h l.

Задача № 14 . Алюминиевый шарик диаметром d = 3 мм падает в масле с постоянной скоростью V = 3 см / с. Определить кинематическую вязкость масла, имеющего плотность r = 0 , 88 г /см3.

Задача № 15 . Труба имеет внезапное расширение от диаметра d 1 = 100 мм до диаметра d 2 = 300 мм . Определить потерю напора h м и коэффициент местного сопротивления, если объемный расход Q = 35 , 3 л / с.

Задача № 16 . Определить коэффициент скорости j при истечении воды из внешне-го горизонтального цилиндрического насадка, снабженного на конце вентилем и коленом, изогнутым под прямым углом. Отношение диаметра насадка d к радиусу закругления колена R d / R = 0 , 2 ; отношение полной длины насадка l к его диаметру d l / d = 10 ; коэффициент сопротивления входа в насадок z = 1 , 2 ; коэффициент трения l = 0 , 02 .

Задача № 17 . Определить начальную скорость истечения воды из отверстия в дне сосуда, заполненного слоями воды и масла одинаковой толщины 1 м. Относительная плотность масла 0,8 . Потерями напора пренебречь.

Задача № 18 . Определить расход воды, вытекающей из трубы ( рис. 3 ) , по данным табл.3.

Видео:Урок 194. Уравнение Ван-дер-ВаальсаСкачать