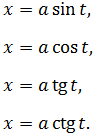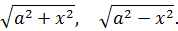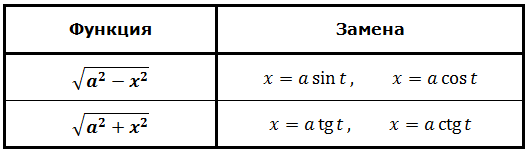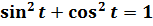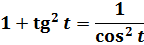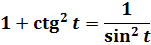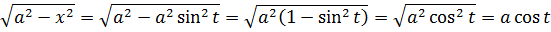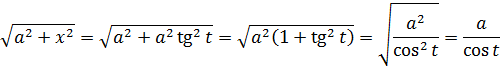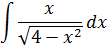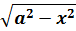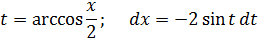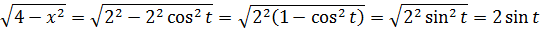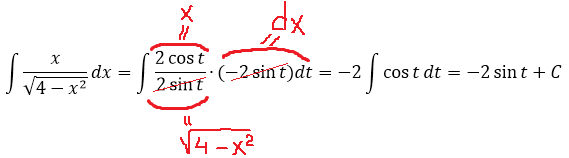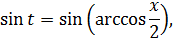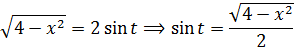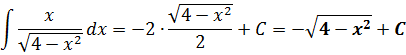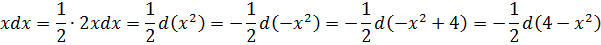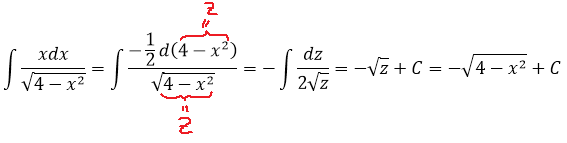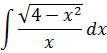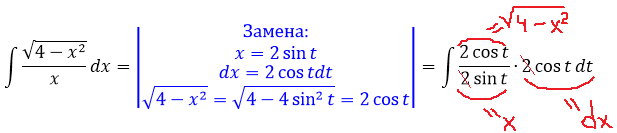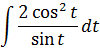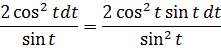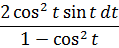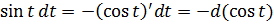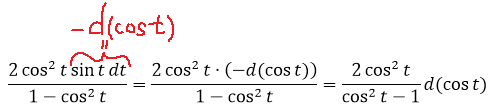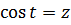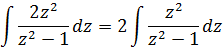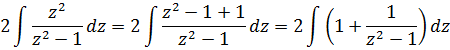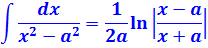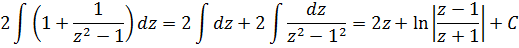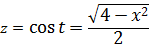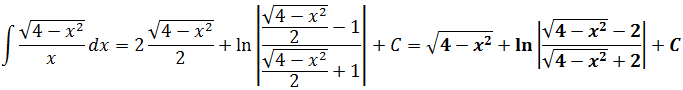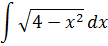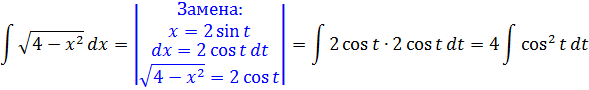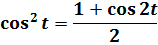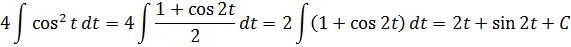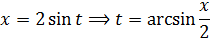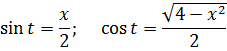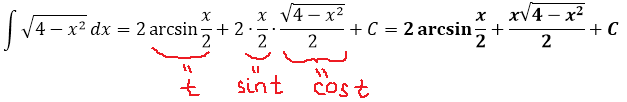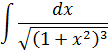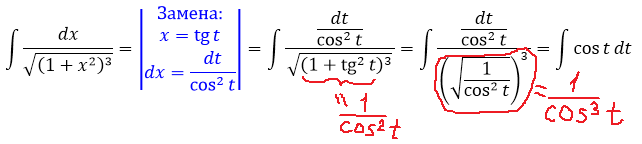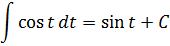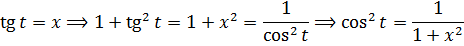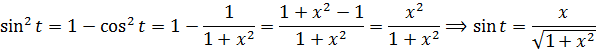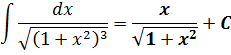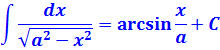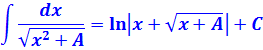Уравнение с заменой через t примеры (8 видео)

Метод замены переменной

Содержание

Метод замены переменной – это такой способ решения, при котором в уравнение (или неравенство) вводится новая переменная, в результате чего оно становится более простым.
Примеры использования метода замены переменной
Биквадратное уравнение. Алгоритм решения и примеры.
Формула биквадратного уравнения:
Как решаются биквадратные уравнения?
Тригонометрическая замена. Интегрируем квадратичные иррациональности!
📺 Видео

Метод замены переменной – это такой способ решения, при котором в уравнение (или неравенство) вводится новая переменная, в результате чего оно становится более простым.

Этот метод один из самых популярных при решении сложных заданий, в частности, в ЕГЭ и ОГЭ.

У нас довольно сложное уравнение. А если раскрыть скобки, оно станет еще сложнее. Что делать? Давайте попробуем заменить переменную.

Заменим выражение (x+frac) буквой (t).

Получилось обычное квадратное уравнение! Решив его, найдем чему равно (t), после чего, сделав обратную замену, вычислим (x).

Когда не стоит вводить новую переменную? Когда это не сделает уравнение проще. Например, если старая переменная остается, несмотря на замену:

Попробуем сделать замену здесь.

Заменим выражение (sin x) буквой (t).

Видим, что в этой замене нет никакого смысла – она не упростила уравнение, даже наоборот, усложнила его, потому что теперь у нас в уравнении две переменные.

Видео:Решение уравнения методом замены переменнойСкачать

Примеры использования метода замены переменной

Заметим, что (x^4=(x^2 )^2) (см. свойства степеней ). Тогда наше уравнение приобретает следующий вид.

Теперь используем метод замены.

Вводим новую переменную, заменяя (x^2) на (t).

Мы нашли чему равно (t), но найти-то надо иксы! Поэтому делаем обратную замену.

Ответ: (±1); (±) (frac) .

Весьма частая ошибка при использовании этого метода: забыть «вернуться к иксам», то есть не сделать обратную замену. Помните – нам нужно найти (x), а не (t)! Поэтому возврат к (x) — строго обязателен!

Пример. Решить неравенство: (log^2_3⁡x-log_3⁡x-2>0)

Приступим к решению.

Раскладываем левую часть неравенства на множители .

Теперь нужно вернуться к исходной переменной – иксу. Для этого перейдем к совокупности , имеющей такое же решение, и сделаем обратную замену.

Видео:СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

Биквадратное уравнение. Алгоритм решения и примеры.

Биквадратные уравнения относятся к разделу школьной алгебры. Метод решения таких уравнений довольно простой, нужно использовать замену переменной.
Рассмотрим алгоритм решения:
-Что такое биквадратное уравнение?
-Как решить биквадратное уравнение?
-Метод замены переменной.
-Примеры биквадратного уравнения.
-Нахождение корней биквадратного уравнения.

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Формула биквадратного уравнения:

Формулы биквадратного уравнения отличается от квадратного уравнения тем, что у переменной х степени повышатся в два раза.

ax 4 +bx 2 +c=0, где a≠0

Видео:10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

Как решаются биквадратные уравнения?

Решение биквадратных уравнений сводится сначала к замене, а потом решению квадратного уравнения:
(x^=t,;tgeq0)
t должно быть положительным числом или равным нулю

Получаем квадратное уравнение и решаем его:
at 2 +bt+c=0,
где x и t — переменная,
a, b, c -числовые коэффициенты.

(t^-5t+6=0)
Получилось полное квадратное уравнение, решаем его через дискриминант:
(D=b^-4ac=(-5)^-4times1times6=25-24=1)
Дискриминант больше нуля, следовательно, два корня, найдем их:

Возвращаемся в замену, подставим вместо переменной t полученные числа: (x^=3)
Чтобы решить такого вида уравнение, необходимо обе части уравнения занести под квадратный корень.

Получилось полное квадратное уравнение, решаем через дискриминант:
(D=b^-4ac=(-4)^-4times1times4=16-16=0)
Дискриминант равен нулю, следовательно, один корень, найдем его:
(t=frac=frac=2)

Возвращаемся в замену, подставим вместо переменной t полученное число:

Можно не во всех случаях делать замену. Рассмотрим пример.

Пример №3:
Решить биквадратное уравнение.

Выносим переменную x 2 за скобку,

Приравниваем каждый множитель к нулю

Делим всё уравнение на -4:
Чтобы решить (x^=4) такое уравнение, необходимо, обе части уравнения занести под квадратный корень.
(begin
&x^=4\
&x_=2\
&x_=-2\
end)

Пример №4:
Решите биквадратное уравнение.
(x^-16=0)

Возвращаемся в замену, подставим вместо переменной t полученное число:
(begin
&x^=4\
&x_=2\
&x_=-2
end)

Ответ: решения нет.

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.

Видео:Дробно-рациональные уравнения. 8 класс.Скачать

Тригонометрическая замена. Интегрируем квадратичные иррациональности!

Итак, друзья, продолжаем знакомиться с типовыми заменами при вычислении неопределённых интегралов. В прошлый раз мы познакомились с наиболее часто употребляемой степенной заменой, усвоили, как и где именно она применяется, порешали несложные примеры с корнями. Суть степенной замены заключалась в том, что старая переменная интегрирования икс заменялась степенной функцией от новой переменной t. И после такой замены у нас пропадали все корни.

В этом уроке речь пойдёт о так называемой тригонометрической замене. Суть её тоже очень простая и заключается в следующем: старая переменная икс заменяется на некоторую… тригонометрическую функцию от t. Да-да! Всего возможно четыре варианта:

Параметр а — некоторая положительная константа. Зачем она там нужна, станет ясно чуть ниже. На примерах.)

А теперь будем разбираться, где именно применяется такая замена и что она нам даёт. Заодно и элементарную тригонометрию повторим. 🙂

Тригонометрическая замена, так же, как и степенная, применяется при интегрировании некоторых функций с корнями. Только, в отличие от степенной замены, для тригонометрической есть два важных условия её применения:

1) Подынтегральная функция содержит квадратный (и только квадратный!) корень;

2) Под корнем стоит квадратичная конструкция вида a 2 ±x 2 .

Иными словами, в сегодняшнем уроке речь пойдёт о вычислении интегралов, содержащих вот такие корни:

Для плюса и для минуса используется своя замена. Вот вам небольшая сводная табличка:

Выбирать можно любую из предложенных подстановок: для минуса хоть синус, хоть косинус, а для плюса — либо тангенс, либо котангенс. Что больше нравится. 🙂

Суть тригонометрической замены полностью аналогична — убрать корень. То есть, добиться того, чтобы под корнем получился точный квадрат и корень извлекался начисто. И, тем самым, исчез из примера.)

Как же это происходит? Для полного понимания нам понадобится три до боли знакомых школьных тождества:

А теперь возьмём какой-нибудь из корней (пусть первый корень, с минусом в подкоренном выражении) и подставим в него нашу замену (допустим, с синусом a·sin t). Что у нас получится:

Для корня с плюсом проделаем всё то же самое, но на примере подстановки с тангенсом:

Вот и вся суть. Был корень — и нету корня! Возможно, кто-то хмыкнет скептически: какая, мол, разница, корень под интегралом или тригонометрия?! Хрен редьки не слаще… А в чём-то тригонометрия даже и похуже корней будет!

Что ж, настало время удивить скептиков. На примерах.) Итак, начнём!

Пример 1

Подынтегральная функция содержит корень вида

Число а у нас — двойка: 4 = 2 2 . Раз под корнем минус, то используем замену либо с синусом, либо с косинусом. Давайте, с косинусом возьмём. Для разнообразия.)

Итак, замена: x = 2cos t

Сразу же можно выразить само t, а также dx:

А теперь, используя нашу замену, упрощаем сам корень, который нам так мешает:

Вот и отлично. Корня больше нет. Теперь посмотрим, что же у нас получится под интегралом после такой замены:

И как вам? Был интеграл от ужасного корня, а после замены стал табличный (!) интеграл. От косинуса, правда, ну и что в этом страшного? 🙂

Осталось лишь вернуться обратно к переменной икс и записать ответ. Только я не буду сейчас тупо в лоб считать что-то типа

а сразу найду синус t из равенства, где мы упрощали наш корень:

Всё. Подставляем это выражение в наш результат вместо sin t и окончательно получаем:

И все дела.) Да-да, вот такой вот простенький ответ у этого примера.) Можете даже в уме его продифференцировать и получить подынтегральную функцию. 🙂

Особо глазастые студенты при первом взгляде на пример, возможно, узрели вот такую взаимосвязь:

Что ж, респект глазастым! 🙂 Да, действительно, если внести подкоренное выражение 4-х 2 под дифференциал, то пример элементарно сведётся к табличной степенной функции:

Можно так интегрировать? А почему — нет? Математика не запрещает. Но нам ведь размяться с тригонометрической заменой нужно! Вот и изучаем на несложном примере. 🙂

А теперь пример посложнее. Поменяем местами в нашей подынтегральной функции числитель и знаменатель. То есть, просто перевернём подынтегральную функцию. Вот такой пример будем решать:

Пример 2

Давайте, в этот раз используем замену с синусом. Сразу пишем:

И теперь, после подстановки, наш новый интеграл стал выглядеть вот так:

Что делать дальше? Главное — не бояться! И смекалки немного. 🙂

Вообще говоря, на такого рода функции есть свой приём интегрирования (тоже замена, кстати), но мы пока сделаем вид, что про неё не знаем. 🙂 И попробуем выкрутиться с помощью элементарных преобразований, которые мы с вами уже знаем. )

Что здесь можно сделать? Ну, напрашивается подведение под дифференциал, ибо в дроби сидят синус и косинус — родственнички по производной.) Для этого надо попробовать преобразовать подынтегральное выражение так, чтобы везде осталась одна функция — либо синус, либо косинус. Здесь можно всё свести к косинусу. Смотрите, как это делается! По пунктам:

1. Умножаем числитель и знаменатель дроби (вместе с dt!) на sin t. Что именно это даст — узнаем дальше.

2. Заменяем в знаменателе sin 2 t на 1-cos 2 t. Согласно основному тригонометрическому тождеству, ага. 🙂

и подводим косинус под знак дифференциала (про минус тоже не забываем, да).

Вот так. Теперь всё подынтегральное выражение у нас сведено к косинусу. Я согласен, что ещё надо было додуматься домножить всё на sin t, чтобы выйти на такую комбинацию. Но тут уже только богатый опыт рулит. Такое чутьё приходит только с практикой. Так что — решайте примеры! Чем больше, тем лучше.)

Итак, теперь смело заменяем косинус новой буквой. Тэ у нас уже использовано, пусть зэт будет:

Выражаем наш интеграл теперь уже через переменную z:

А теперь в дело вступает наш старый добрый излюбленный приёмчик — отнять/прибавить единичку. 🙂 Продолжаем:

Единичка, я надеюсь, ни у кого проблем в интегрировании не вызывает? А что же касается дроби 1/(z 2 -1), то это не что иное, как табличный интеграл! Открывайте нашу таблицу и ищите похожую формулу. Это седьмая формула, с «высоким» логарифмом:

В роли «а» у нас выступает единичка. Возвращаемся к нашим баранам:

Что ж, заготовка для ответа получена. Теперь поэтапно возвращаемся обратно к иксу:

Вот такой вот интересный пример. И довольно красивый ответ.)

Маньяки могут его продифференцировать. Я продифференцировал. Всё гуд.)

Продолжаем развлекаться. 🙂 Теперь вообще уберём знаменатель и решим вот такой примерчик:

Пример 3

Под интегралом теперь стоит просто чистый корень, безо всего. И тут тоже на помощь придёт тригонометрическая замена.) Давайте, снова будем всё выражать через синус, ибо он удобнее: минус лишний не всплывает, который легко потерять. Действуем:

Как теперь быть с косинусом в квадрате? Если в прошлом примере нам пришлось домножать всё на синус, то тут всё гораздо проще. Призываем на помощь школьную тригонометрию! На сей раз — формулы понижения степени. А чуть конкретнее — вот эту:

И после такого преобразования наш интеграл легко превращается в сумму табличных (ну, или почти табличных :)):

Надеюсь, особо не нужно комментировать, как именно при интегрировании получился синус двух t? Кто не понял — читаем урок « Подведение функции под знак дифференциала ». Там всё популярно изложено. 🙂

Всё. «Рыба» для ответа готова. Осталось правильно перейти к иксу да подставить вместо t в выражения 2t и sin 2t.

Прежде всего, выясним из нашей замены, что же такое это самое t:

Теперь раскроем синус двойного угла: sin2t = 2sin t·cos t

Зачем так сделано? А затем, что теперь и синус и косинус легко выражаются через x (смотрим синюю табличку с нашей заменой)! Вот так:

И теперь наш окончательный ответ полностью готов:

Ну как? Да, я согласен, не самые простые примеры. Так и мы с вами уже всё-таки на приличном уровне, правда?

Что-то мы всё с синусами да косинусами возимся, а тангенс/котангенс как-то обделили вниманием. Давайте и такой примерчик рассмотрим! На десерт.) Он совсем несложный: хватит с вас жести на сегодня! 🙂 Просто чтобы суть замены уловить.)

Пример 4

Не пугаемся внешнего вида примера! Внешность иногда бывает обманчива, да.)

Сразу замечаем под корнем сумму 1+х 2 . Раз сумма, то, стало быть, подходящая замена для ликвидации корня — с тангенсом (или котангенсом). Опять же, по причине нежелания возиться с лишним минусом, я выберу тангенс (а = 1, x = tg t):

И снова перед нами безобидный табличный интеграл! Интегрируем косинус и — готово дело:

Всё. Выражаем теперь нашу первообразную через икс. Как? По формулам тригонометрии, вестимо! У нас есть тангенс, а нас интересует синус.

Так. Квадрат косинуса готов. Осталось лишь из основного тригонометрического тождества вытащить квадрат синуса, извлечь корень и — цель достигнута!

Вот и наш ответ. Довольно простенький на сей раз:

Подытожим наш урок. Давайте разберёмся, зачем в самом начале урока я высказал два обязательных требования, чтобы сам корень был только квадратным (а не кубическим или какой-то более высокой степени), а также чтобы под корнем находилась конструкция вида x 2 ±a 2 . Догадались, почему?

Да потому, что в любой другой ситуации (кубический корень или же под корнем многочлен более высокой степени) у нас просто-напросто не исчезнет иррациональность, и данная замена нам уже никак не поможет свести интеграл к красивому виду. 🙂 И, если вам, вдруг, попался такой пример, то, скорее всего, преобразования более хитрые.

Разумеется, подобные интегралы не ограничиваются этими четырьмя примерами. И для интегралов, содержащих квадратичные иррациональности, есть и более суровые подстановки — Эйлера и Абеля. Но такие подстановки — уже высший пилотаж в интегрировании. Их мы будем изучать ближе к концу раздела. Зато тщательный разбор этих четырёх примеров даст вам возможность уверенно брать хотя бы некоторые интегралы подобного типа. Так что тригонометрическая замена — штука весьма полезная. Мы с ней дружить будем. 🙂 А для дружбы, конечно же, необходимо хорошо знать школьную тригонометрию — основные тождества (их шесть), двойные углы, формулы понижения степени и т.д.

Что ж, на сегодня хватит. А в качестве тренировочного упражнения в этот раз я дам небольшое творческое задание. Чтобы скучно не было.)

Есть в нашей замечательной табличке интегралов парочка довольно страшных формул. Вот эти:

И теперь, в качестве задания, я предлагаю вам доказать эти формулы! С помощью тригонометрической замены, да.) Чтобы вы прочувствовали, откуда что в математике берётся. И берётся явно не с потолка.)

С первой формулой проблем возникнуть не должно: там всё очевидно. А вот со второй («длинным логарифмом») я немного подскажу. В формуле число А для определённости предполагается положительным. Раз оно положительное, то можно совершенно спокойно заменить это самое А на a 2 . И дальше работать уже с заменой через тангенс.) Материала этого (и прошлых) уроков вполне достаточно, чтобы одолеть это задание. Будет вам там парочка сюрпризов! Выручат свойства логарифмов и первообразных (это подсказка! :)).