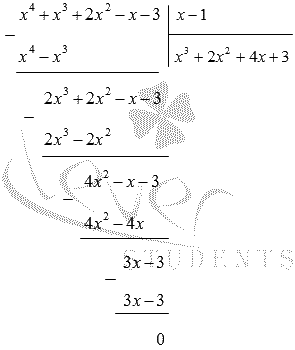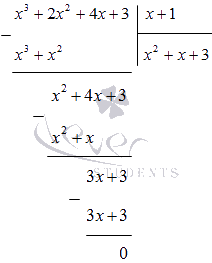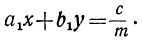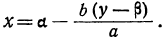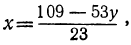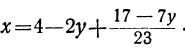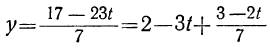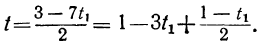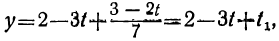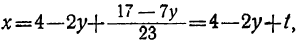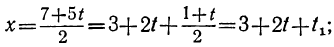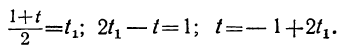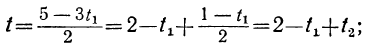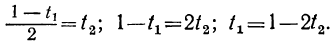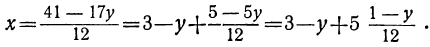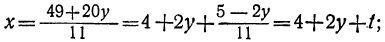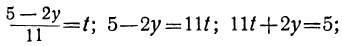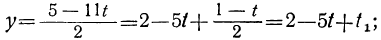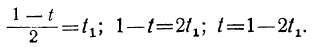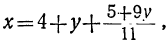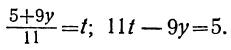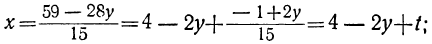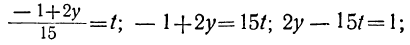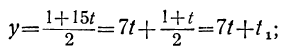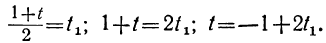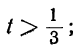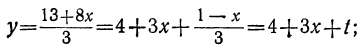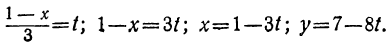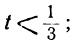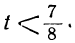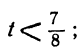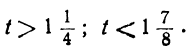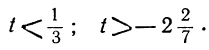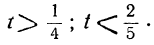В общем случае уравнение, имеющее степень выше 4 , нельзя разрешить в радикалах. Но иногда мы все же можем найти корни многочлена, стоящего слева в уравнении высшей степени, если представим его в виде произведения многочленов в степени не более 4 -х. Решение таких уравнений базируется на разложении многочлена на множители, поэтому советуем вам повторить эту тему перед изучением данной статьи.
Чаще всего приходится иметь дело с уравнениями высших степеней с целыми коэффициентами. В этих случаях мы можем попробовать найти рациональные корни, а потом разложить многочлен на множители, чтобы потом преобразовать его в уравнение более низкой степени, которое будет просто решить. В рамках этого материала мы рассмотрим как раз такие примеры.
- Уравнения высшей степени с целыми коэффициентами
- Схема решения уравнения
- Неопределенные уравнения в математике с примерами решения и образцами выполнения
- Признак невозможности решения уравнения в целых числах
- Признак невозможности решения уравнения в положительных числах
- Общая формула корней неопределённого уравнения
- Способ подстановки
- Общее решение неопределённого уравнения
- Положительные решения
- Решение уравнений в целых числах
- Математика, 9 класс
- , ДВГГУ
- Решение уравнений в целых числах
- 💡 Видео
Видео:Математика для всех. Алексей Савватеев. Лекция 6.8. Корни многочленов с целыми коэффициентамиСкачать

Уравнения высшей степени с целыми коэффициентами
Все уравнения, имеющие вид a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = 0 , мы можем привести к уравнению той же степени с помощью умножения обеих частей на a n n — 1 и осуществив замену переменной вида y = a n x :
a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = 0 a n n · x n + a n — 1 · a n n — 1 · x n — 1 + … + a 1 · ( a n ) n — 1 · x + a 0 · ( a n ) n — 1 = 0 y = a n x ⇒ y n + b n — 1 y n — 1 + … + b 1 y + b 0 = 0
Те коэффициенты, что получились в итоге, также будут целыми. Таким образом, нам нужно будет решить приведенное уравнение n-ной степени с целыми коэффициентами, имеющее вид x n + a n x n — 1 + … + a 1 x + a 0 = 0 .
Видео:Как решать Диофантовы уравнения ★ 9x+13y=-1 ★ Решите уравнение в целых числахСкачать

Схема решения уравнения
Вычисляем целые корни уравнения. Если уравнение имеет целые корни, нужно искать их среди делителей свободного члена a 0 . Выпишем их и будем подставлять в исходное равенство по очереди, проверяя результат. Как только мы получили тождество и нашли один из корней уравнения, то можем записать его в виде x — x 1 · P n — 1 ( x ) = 0 . Здесь x 1 является корнем уравнения, а P n — 1 ( x ) представляет собой частное от деления x n + a n x n — 1 + … + a 1 x + a 0 на x — x 1 .
Подставляем остальные выписанные делители в P n — 1 ( x ) = 0 , начав с x 1 , поскольку корни могут повторяться. После получения тождества корень x 2 считается найденным, а уравнение может быть записано в виде ( x — x 1 ) ( x — x 2 ) · P n — 2 ( x ) = 0 .Здесь P n — 2 ( x ) будет частным от деления P n — 1 ( x ) на x — x 2 .
Продолжаем и дальше перебирать делители. Найдем все целые корни и обозначим их количество как m . После этого исходное уравнение можно представить как x — x 1 x — x 2 · … · x — x m · P n — m ( x ) = 0 . Здесь P n — m ( x ) является многочленом n — m -ной степени. Для подсчета удобно использовать схему Горнера.
Если у нас исходное уравнение имеет целые коэффициенты, мы не можем получить в итоге дробные корни.
У нас в итоге получилось уравнение P n — m ( x ) = 0 , корни которого могут быть найдены любым удобным способом. Они могут быть иррациональными или комплексными.
Покажем на конкретном примере, как применяется такая схема решения.
Условие: найдите решение уравнения x 4 + x 3 + 2 x 2 — x — 3 = 0 .
Решение
Начнем с нахождений целых корней.
У нас есть свободный член, равный минус трем. У него есть делители, равные 1 , — 1 , 3 и — 3 . Подставим их в исходное уравнение и посмотрим, какие из них дадут в итоге тождества.
При x , равном единице, мы получим 1 4 + 1 3 + 2 · 1 2 — 1 — 3 = 0 , значит, единица будет корнем данного уравнения.
Теперь выполним деления многочлена x 4 + x 3 + 2 x 2 — x — 3 на ( х — 1 ) в столбик:
Значит, x 4 + x 3 + 2 x 2 — x — 3 = x — 1 x 3 + 2 x 2 + 4 x + 3 .
Перебираем возможные делители дальше, но подставляем их в равенство x 3 + 2 x 2 + 4 x + 3 = 0 :
1 3 + 2 · 1 2 + 4 · 1 + 3 = 10 ≠ 0 ( — 1 ) 3 + 2 · ( — 1 ) 2 + 4 · — 1 + 3 = 0
У нас получилось тождество, значит, мы нашли еще один корень уравнения, равный — 1 .
Делим многочлен x 3 + 2 x 2 + 4 x + 3 на ( х + 1 ) в столбик:
x 4 + x 3 + 2 x 2 — x — 3 = ( x — 1 ) ( x 3 + 2 x 2 + 4 x + 3 ) = = ( x — 1 ) ( x + 1 ) ( x 2 + x + 3 )
Подставляем очередной делитель в равенство x 2 + x + 3 = 0 , начиная с — 1 :
— 1 2 + ( — 1 ) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 ( — 3 ) 2 + ( — 3 ) + 3 = 9 ≠ 0
Равенства, полученные в итоге, будут неверными, значит, у уравнения больше нет целых корней.
Оставшиеся корни будут корнями выражения x 2 + x + 3 .
D = 1 2 — 4 · 1 · 3 = — 11 0
Из этого следует, что у данного квадратного трехчлена нет действительных корней, но есть комплексно сопряженные: x = — 1 2 ± i 11 2 .
Уточним, что вместо деления в столбик можно применять схему Горнера. Это делается так: после того, как мы определили первый корень уравнения, заполняем таблицу.
| x i | коэффициенты многочлена | ||||
| 1 | 1 | 2 | — 1 | — 3 | |
| 1 | 1 | 1 + 1 · 1 = 2 | 2 + 2 · 1 = 4 | — 1 + 4 · 1 = 3 | — 3 + 3 · 1 = 0 |
В таблице коэффициентов мы сразу можем увидеть коэффициенты частного от деления многочленов, значит, x 4 + x 3 + 2 x 2 — x — 3 = x — 1 x 3 + 2 x 2 + 4 x + 3 .
После нахождения следующего корня, равного — 1 , мы получаем следующее:
| x i | коэффициенты многочлена | |||
| 1 | 2 | 4 | 3 | |
| 1 | 1 | 2 + 1 · ( — 1 ) = 1 | 4 + 1 · ( — 1 ) = 3 | 3 + 3 · ( — 1 ) = 0 |
Далее мы приходим к разложению x — 1 x + 1 x 2 + x + 3 = 0 . Потом, проверив оставшиеся делители равенства x 2 + x + 3 = 0 , вычисляем оставшиеся корни.
Ответ: х = — 1 , х = 1 , x = — 1 2 ± i 11 2 .
Условие: решите уравнение x 4 — x 3 — 5 x 2 + 12 = 0 .
Решение
У свободного члена есть делители 1 , — 1 , 2 , — 2 , 3 , — 3 , 4 , — 4 , 6 , — 6 , 12 , — 12 .
Проверяем их по порядку:
1 4 — 1 3 — 5 · 1 2 + 12 = 7 ≠ 0 ( — 1 ) 4 — ( — 1 ) 3 — 5 · ( — 1 ) 2 + 12 = 9 ≠ 0 2 4 · 2 3 — 5 · 2 2 + 12 = 0
Значит, x = 2 будет корнем уравнения. Разделим x 4 — x 3 — 5 x 2 + 12 на х — 2 , воспользовавшись схемой Горнера:
| x i | коэффициенты многочлена | ||||
| 1 | — 1 | — 5 | 0 | 12 | |
| 2 | 1 | — 1 + 1 · 2 = 1 | — 5 + 1 · 2 = — 3 | 0 — 3 · 2 = 3 | 12 — 6 · 2 = 0 |
В итоге мы получим x — 2 ( x 3 + x 2 — 3 x — 6 ) = 0 .
Проверяем делители дальше, но уже для равенства x 3 + x 2 — 3 x — 6 = 0 , начиная с двойки.
2 3 + 2 2 — 3 · 2 — 6 = 0
Значит, 2 опять будет корнем. Разделим x 3 + x 2 — 3 x — 6 = 0 на x — 2 :
| x i | коэффициенты многочлена | |||
| 1 | 1 | — 3 | — 6 | |
| 2 | 1 | 1 + 1 · 2 = 3 | — 3 + 3 · 2 = 3 | — 6 + 3 · 2 = 0 |
В итоге получим ( x — 2 ) 2 · ( x 2 + 3 x + 3 ) = 0 .
Проверка оставшихся делителей смысла не имеет, поскольку равенство x 2 + 3 x + 3 = 0 быстрее и удобнее решить с помощью дискриминанта.
Решим квадратное уравнение:
x 2 + 3 x + 3 = 0 D = 3 2 — 4 · 1 · 3 = — 3 0
Получаем комплексно сопряженную пару корней: x = — 3 2 ± i 3 2 .
Ответ: x = — 3 2 ± i 3 2 .
Условие: найдите для уравнения x 4 + 1 2 x 3 — 5 2 x — 3 = 0 действительные корни.
Решение
x 4 + 1 2 x 3 — 5 2 x — 3 = 0 2 x 4 + x 3 — 5 x — 6 = 0
Выполняем домножение 2 3 обеих частей уравнения:
2 x 4 + x 3 — 5 x — 6 = 0 2 4 · x 4 + 2 3 x 3 — 20 · 2 · x — 48 = 0
Заменяем переменные y = 2 x :
2 4 · x 4 + 2 3 x 3 — 20 · 2 · x — 48 = 0 y 4 + y 3 — 20 y — 48 = 0
В итоге у нас получилось стандартное уравнение 4 -й степени, которое можно решить по стандартной схеме. Проверим делители, разделим и получим в итоге, что оно имеет 2 действительных корня y = — 2 , y = 3 и два комплексных. Решение целиком здесь мы не будем приводить. В силу замены действительными корнями данного уравнения будут x = y 2 = — 2 2 = — 1 и x = y 2 = 3 2 .
Ответ: x 1 = — 1 , x 2 = 3 2
Советуем также ознакомиться с материалами, посвященными решению кубических уравнений и уравнений четвертой степени.
Видео:Рациональные корни многочлена с целым показателем. 10 класс.Скачать

Неопределенные уравнения в математике с примерами решения и образцами выполнения
При изучении уравнений первой степени мы уже видели, что если число уравнений меньше числа неизвестных, то такая система имеет бесчисленное множество решений. Такие уравнения называются неопределёнными.
Наиболее часто в практике встречается случай одного уравнения с двумя неизвестными. Общий вид такого уравнения будет:
αx+by=c,
где x и у—неизвестные, а, b и с—данные коэффициенты.
Часто условия задачи бывают таковы, что правильный ответ на вопрос, поставленный в задаче, дают только целые значения, а иногда только целые и притом положительные значения.
Задача:
Разложить число 118 на такие два числа, из которых одно делилось бы на 11, а другое на 17.
Обозначая одно число через Их, а другое через 17у, мы получим уравнение:
11x+17y=118.
Так как в задаче ничего не сказано о знаке чисел, на которые нужно разложить число 118, то в данном случае мы можем считать ответом на задачу и отрицательные решения. Так, условию задачи удовлетворяют числа 33 и 85 (при х=3 и у=5), но также удовлетворяют и числа 220 и —102 (при х=20 и у=—6).
Задача:
Для упаковки самоваров имеются ящики, из которых в одни укладываются 4 самовара, в другие 7. Сколько нужно взять тех или других ящиков, чтобы упаковать 41 самовар?
Обозначив число малых ящиков через х, а число больших через у, будем иметь уравнение:
4x-+7y=41.
Очевидно, что по условию задачи здесь пригодны только целые и притом положительные решения. Такое решение данное уравнение допускает лишь одно, именно: x=5, у=3.
Таким образом, необходимо уметь решать неопределённые уравнения в целых числах, а также в целых и положительных числах.
Видео:Классический способ решения Диофантовых уравнений ➜ Решите уравнение в целых числах ➜ 13x-7y=6Скачать

Признак невозможности решения уравнения в целых числах
Если среди коэффициентов а, b и с имеются дробные, то мы можем привести все коэффициенты к одному знаменателю и затем его отбросить. Тогда все коэффициенты будут целыми числами.
Далее, если а, b и с имеют какой-либо общий множитель, то на него можно сократить обе части уравнения.
Итак, мы будем предполагать, что коэффициенты a, b и с —числа целые, не имеющие общего множителя.
Предположим теперь, что а и b имеют общим множителем некоторое целое число, отличное от 1. Пусть, например,
a=ma₁, b=mb₁.
Разделив все его члены на m, получим:
При целых значениях х и у левая часть уравнения представляет собой целое число, правая же часть — дробь, так как с, по предположению, не делится на m. Такое равенство невозможно. Следовательно:
Если коэффициенты при неизвестных неопределённого уравнения имеют общий множитель, которого не имеет свободный член, то уравнение не может иметь целых решений.
Поэтому во всех дальнейших рассуждениях мы будем предполагать числа а и b взаимно простыми.
Видео:Решите уравнение в целых числах 5x-4y=3 ➜ Как решать Диофантовы уравнения?Скачать

Признак невозможности решения уравнения в положительных числах
Пусть в уравнении ax+by=c коэффициенты а и b положительны, а свободный член с — отрицателен. Тогда при всяких положительных значениях х и у левая часть уравнения будет положительной, а правая останется отрицательной. Такое равенство невозможно.
Если коэффициенты а и b отрицательны, а с — положительно, то, умножив все члены уравнения на —1, мы сведём этот случай к предыдущему. Итак:
Если коэффициенты при неизвестных неопределённого уравнения имеют знаки, противоположные знаку свободного члена, то уравнение не имеет положительных решений.
Видео:Решение уравнений в целых числахСкачать

Общая формула корней неопределённого уравнения
Предположим, что каким-либо способом (например, путём непосредственных проб) мы нашли одно целочисленное решение неопределённого уравнения:
ax+by=с.
Пусть это решение будет х=а и y=β. Подставляя значение x и у в данное уравнение, получим тождество:
a a+bβ =c.
Вычитая почленно это тождество из данного уравнения, получим:
α(x-α)+b(y-β)=0,
откуда:
ax=aa — b(y—β), или
Для того чтобы x было целым числом, необходимо и достаточно, чтобы выражение было целым числом (так как а—число
целое). Другими словами, необходимо и достаточно, чтобы выражение b(y-β) нацело делилось на а. Но, по предположению, b — число взаимно простое с а, следовательно, необходимо (и достаточно), чтобы разность у—β нацело делилась на а. Обозначив целое частное от деления у— β на а через t (оно может быть и положительным и отрицательным), получим:
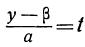
Подставляя в формулу для х число t вместо дроби 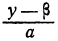
x = a-bt.
Таким образом, мы имеем для корней неопределённого уравнения формулы:
x = a-bt, y=β+at.
Давая в этих формулах t произвольные целые значения, положительные и отрицательные, мы получим бесчисленное множество целых решений данного неопределённого уравнения. В частности, при t=0 получим решение х = а; y=β, найденное нами уже ранее.
Присматриваясь к найденным формулам, легко заметить, что они составлены по следующему правилу:
- Первым членом формулы является найденное частное значение данного неизвестного.
- Вторым членом формул является произвольное целое число t, умноженное на коэффициент данного уравнения, причём в формуле для x берётся коэффициент при у в данном уравнении, а в формуле для у берётся коэффициент при х.
- Один из коэффициентов берётся с обратным знаком.
Нетрудно видеть, что совершенно безразлично, который из коэффициентов мы берём с тем же знаком, с каким он стоит в уравнении и который берём с обратным знаком. В самом деле, формулы:
x=a-bt, y=β+at и x=a+bt, y=β -at
будут давать одни и те же решения; только те решения, которые одни формулы дают при положительных значениях t, другие будут давать при равных по абсолютной величине отрицательных значениях t.
Пример:
Непосредственной подстановкой убеждаемся, что уравнение удовлетворяется значениями х=2 и у=4. Тогда все остальные решения найдутся из формул:
x=2+5t, у=4—3t, или х=2—5t, y=4+3t.
Давая в этих формулах t произвольные целые значения, будем получать различные целочисленные решения данного уравнения. Например, взяв первые формулы, будем иметь:
| t | 0 | 1 | 2 | 3 | -1 | -2 | … |
| x | 2 | 7 | 12 | 17 | -3 | -8 | … |
| y | 4 | 1 | -2 | -5 | 7 | 10 | … |
Если бы мы взяли вторые формулы, то те же решения получили бы, давая t последовательно значения: 0; —1; —2; —3; 1; 2 и т. д.
Таким образом, задача решения в целых числах неопределенного уравнения сводится к нахождению какого-либо одного решения.
Способ подстановки
Для нахождения одного решения неопределённого уравнения можно пользоваться следующим способом. Пусть дано уравнение:
ах+by=с.
Определим из него одно из неизвестных в зависимости от другого (лучше взять то, у которого коэффициент меньше). Пусть, например, a Частный вид неопределённого уравнения
Неопределённое уравнение легко решается в общем виде, когда один из коэффициентов при неизвестных равен единице. Пусть, например, равен единице коэффициент при х. Будем иметь:
x+by=c.
Определим х:
x=c-by.
Очевидно, что любому целому значению у будет соответствовать целое же значение х.
Пример:
Дано уравнение: 5x+y=18.
Находим:
у = 18—5х.
Давая x произвольные целые значения, будем соответственно получать целые значения для у:
| x | 0 | 1 | 2 | 3 | 4 | -1 | -2 | … |
| y | 18 | 13 | 8 | 3 | -2 | 23 | 28 | … |
Видео:Рациональные и целые корни многочленов с целыми коэффициентамиСкачать

Общее решение неопределённого уравнения
Покажем на примере способ решения неопределённого уравнения с любыми коэффициентами. Пусть дано уравнение:
23x+53y=109.
Определим из этого уравнения то неизвестное, у которого коэффициент меньше, в данном случае х:
или, исключив целую часть:
Для того чтобы x было целым при у целом, необходимо и достаточно, чтобы выражение 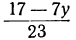
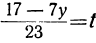
Если мы найдём для у и t такие целые значения, которые удовлетворяют уравнению 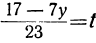
23t+7y=17,
то тем самым мы найдём соответствующие целые значения для х, и наша задача будет решена. Таким образом, решение данного уравнения мы свели к решению другого, более простого уравнения, у которого коэффициенты меньше, чем у данного.
По отношению к новому уравнению поступаем таким же образом. Определяем из него у:
Для того чтобы у было целым, необходимо и достаточно, чтобы 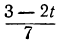
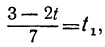
При целых t и t₁, удовлетворяющих последнему уравнению, мы получим соответственно целые значения для х и у, удовлетворяющие данному уравнению. Следовательно, наша задача свелась к решению последнего уравнения, у которого коэффициенты ещё меньше. Поступаем с ним так же, как и прежде:
Приравняв выражение 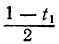
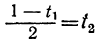
Мы получили уравнение, в котором коэффициент при одном из неизвестных равен единице, а такие уравнения решать мы уже умеем. Решив его, получим:
t₁=1-2t₂.
Давая в этом уравнении произвольные целые значения t₂, будем получать целые значения для t₁. Подставляя найденные целые значения t₁ и t₂ в выражение для t: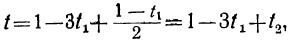
получим соответствующие целые значения для t. Подставляя соответствующие пары значений t и t₁ в выражение для у:
получим соответствующие целые значения для у. Наконец, делая подстановку найденных значений для у и t в выражение для х:
получим соответствующие целые значения для х.
Можно, однако, прямо выразить х и у в зависимости от t₂. Для этого подставим в выражение для t вместо t₁ его выражение через t₂:
t=1-3t₂+t₂=1-3 (1—2t₂)+t₂ ,
или
t=-2+7t₂ .
Подставим теперь в выражение для у вместо t и t₁ их выражения через t₂:
y=2-3t+t₁=2-3(-2+7t₂) + (1- 2t₂),
или
y=9-23t₂.
Наконец, подставляя найденные значения у и t в выражение для х, получим:
x=4-2y+t=4-2(9-23t₂)+(-2+7t₂),
или
x=- 16+53t₂ .
Таким образом, мы получим для х и у формулы:
x= — 16+53t₂, y=9-23t₂.
Давая в них произвольные целые значения для t₂, как положительные, так и отрицательные, будем получать бесчисленное множество решений данного уравнения; некоторые из них помещены в следующей таблице:
| t₂ | 0 | 1 | 2 | -1 | -2 |
| x | -16 | 37 | 90 | -69 | -122 |
| y | 9 | -14 | -37 | 32 | 55 |
Рассматривая операции, которые производились над коэффициентами данного и следующих уравнений, можно заметить такую последовательность:
- Больший коэффициент данного уравнения 53 делили на меньший 23; получили частное 2 и остаток 7.
- Меньший коэффициент данного уравнения 23 делили на остаток 7; получили частное 3 и второй остаток 2.
- Первый остаток 7 делили на второй остаток 2; получили частное 3 и третий остаток 1.
Другими словами, мы поступали точно так, как если бы находили общий наибольший делитель коэффициентов данного уравнения.
Мы знаем, что два взаимно простых числа имеют общим наибольшим делителем единицу. А так как в неопределённом уравнении мы всегда предполагаем коэффициенты при неизвестных взаимно простыми, то производя над уравнением указанные выше операции, мы всегда придём к такому уравнению, у которого коэффициент при одном из неизвестных равен единице. Тем самым мы находим решения и данного уравнения. Отсюда следует:
Если коэффициенты при неизвестных неопределённого уравнения-числа взаимно простые, то уравнение всегда имеет целые решения.
Упрощение решения уравнения. Иногда при решении неопределённого уравнения можно внести некоторые упрощения, позволяющие быстрее прийти к решению.
1. В случае, когда один из коэффициентов при неизвестных и свободный член имеют общий множитель, то на него можно сократить обе части уравнения, если надлежащим образом ввести новое неизвестное.
Пример:
Коэффициент 6 и свободный член имеют общим множителем 3. Следовательно, и член 5у должен делиться на 3, а так как 5 не делится на 3, то у должен быть кратным трём. Полагая у=3t, где t— целое число, будем иметь:
6x-15t=21,
или, по сокращении на 3:
2x-5t =7.
Решаем последнее уравнение:
Подставляя найденное значение в выражения, полученные для х и у, будем иметь:
x=3+2(-1+2t₁)+t₁ =1+5t₁;
y=3(-1+2t₁) = -3+6t₁ .
Пример:
Дано уравнение: 9x+14y=105.
Полагая у=3t и сокращая обе части уравнения на 3, получим:
3x+14t=35.
Полагая в этом уравнении x=7t₁ и сокращая обе части уравнения на 7, получим:
3t₁ +2t=5.
Решаем последнее уравнение:
Произведя последовательные подстановки, получим:
t=2-(1-2t₂) + t₂ = 1+3t₂;
x=7t₁=7(1-2t₂)=7-14t₂ ;
y=3t=3(1+3t₂) = 3+9t₂ .
2. Если в приравниваемом целому числу выражении члены, находящиеся в числителе, имеют общий множитель, то решение уравнения можно упростить.
Пример:
Дано уравнение: 12x+17y=41.
Решаем его относительно х:
Для того чтобы выражение 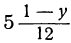
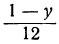
Приравнивая это выражение целому числу t, получим: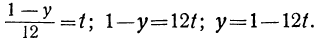
Соответственно получаем для х:
x=3-(1-12t)+5t=2+17t
3. Если при выделении целой части остаток будет более половины делителя, то удобно ввести отрицательный остаток.
Пример:
Дано уравнение: 11х—20y=49.
Решим его относительно х:
Произведя подстановки, получим:
y=2-5(1-2t₁)+t₁ = -3+11t₁;
x=4+2(-3+ 11t₁)+(1-2t₁) = -1+20t₁.
Если бы решали данное уравнение обычным способом, то получили бы для х:
и следующее уравнение было бы:
Это уравнение сложнее уравнения, полученного нами при помощи введения отрицательного остатка:
11t+2y=5.
Пример:
Дано уравнение: 15x+28y=59.
Решаем уравнение относительно х, вводя отрицательные остатки:
Попробовав решить приведённые в примерах уравнения обычным путём, легко убедимся, что без применения указанных упрощений все они потребовали бы для решения большего числа операций.
Положительные решения
Как уже говорилось ранее, часто из всех найденных решений неопределённого уравнения нужно взять лишь те, которые дают одновременно положительные значения для х и у. Найдя общие формулы для х и у, можно сразу определить, при каких значениях произвольного множителя будут получаться целые и положительные значения х и у.
Для того чтобы x и у были положительными, необходимо брать для t только такие значения, при которых:
a+bt>0; β-αt>0.
Будем считать а числом положительным. (Это мы всегда имеем право предположить, так как в противном случае мы могли бы обе части уравнения умножить на —1.) Тогда могут встретиться три различных случая.
1. Оба неравенства одинакового смысла. Это случится когда b — число отрицательное. В самом деле, пользуясь свойствами неравенства, будем иметь:
bt > — a ; at 0; 2+-5t>0,
или
Взяв для t любое целое число, большее 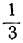
Пример:
Решаем уравнение:
Ищем положительные решения:
1 —3t>0; 7 —8t>0,
или
Любое целое значение t, меньшее 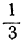
2. Неравенства противоположного смысла, причём они противоречат одно другому. Пусть, например, мы получим следующие неравенства:
Очевидно, что не существует таких значений t, которые одновременно удовлетворяли бы обоим неравенствам. В этом случае уравнение не может иметь положительных решений.
Пример:
4x+5y=-7.
Решая это уравнение, получим:
х=— 3+5t; y=1—4t.
Отсюда:
— 3+5t>0; 1 — 4t>0,
или
Неравенства противоречат друг другу; уравнение не имеет положительных решений.
3. Неравенства противоположного смысла, причём они не противоречат друг другу. Пусть, например, мы получили неравенства:
Все целые значения t, заключающиеся между 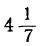
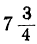
6 и 7, дадут для х и у положительные решения. Таким образом, в этом случае:
Уравнение имеет столько целых положительных решений, сколько целых чисел заключено между найденными пределами для t.
Заметим, что, в частности, уравнение и здесь может не иметь положительных решений. Это будет тогда, когда между найденными пределами для t не содержится ни одного целого числа. Например, пусть мы получим неравенства:
Неравенства не противоречат друг другу, но между 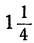
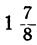
находится ни одного целого числа. Уравнение не имеет целых положительных решений.
Пример:
3x+7y=55.
Решаем уравнение: 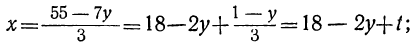
у=1 — 3t; x= 16+7t.
Отсюда:
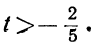
1 —3t>0; 16+7t> 0,
или
Очевидно, для / можно взять лишь значения: 0; —1; —2. Получаем три решения уравнения:
| t | 0 | -1 | -2 |
| x | 16 | 9 | 2 |
| y | 1 | 4 | 7 |
Пример:
5. 5x+4y=3.
Решая уравнение, получим:
х=— 1 + 4t; у=2 —5t.
Отсюда:
Неравенства не противоречат друг другу; но между 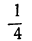
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Алгебра 10 класс (Урок№9 - Решение уравнений в целых числах.)Скачать

Решение уравнений в целых числах
Видео:Уравнение с двумя неизвестными. Решить в целых числах. ЗадачаСкачать

Математика, 9 класс
Видео:Алгебра 9 класс (Урок№21 - Некоторые приёмы решения целых уравнений.)Скачать

, ДВГГУ
Видео:Линейные диофантовы уравненияСкачать

Решение уравнений в целых числах
Решение уравнений в целых числах является одной из древнейших математических задач.
Алгебраическое уравнение с целыми коэффициентами, имеющее более одного неизвестного, когда стоит задача найти его целые или рациональные решения называется неопределенным или диофантовым, по имени древнегреческого математика Диофанта, который занимался проблемой решения таких уравнений. По некоторым данным Диофант жил до 364 года н. э. Достоверно известно лишь своеобразное жизнеописание Диофанта, которое по преданию было высечено на его надгробии и представляло задачу-головоломку: «Бог ниспослал ему быть мальчиком шестую часть жизни; добавив к сему двенадцатую часть, Он покрыл его щеки пушком; после седьмой части Он зажег ему свет супружества и через пять лет после вступления в брак даровал ему сына. Увы! Несчастный поздний ребенок, достигнув меры половины полной жизни отца, он был унесен безжалостным роком. Через четыре года, утешая постигшее его горе наукой о числах, он [Диофант] завершил свою жизнь».
Цель настоящей статьи рассмотреть методы решения некоторых диофантовых уравнений. Многие из этих методов предполагают применение некоторых понятий и алгоритмов теории делимости, в связи с этим, напомним их.
Определение 1. Наибольшим общим делителем (НОД) целых чисел a1, a2,…, an называется такой их положительный общий делитель, который делится на любой другой общий делитель этих чисел.
Теорема 2. Если 

Замечание. Это равенство называется линейной комбинацией или линейным представлением НОД через эти числа.
Определение 3. Числа а и b называются взаимно простыми, если НОД этих чисел равен 1.
Теорема 4. (теорема о делении с остатком) Для любого целого а и целого 

Замечание. Если 




Из теоремы 4 следует, что при фиксированном целом m > 0 любое целое число а можно представить в одном из следующих видов:
При этом если 




На следующей теореме основан способ нахождения наибольшего общего делителя целых чисел.
Теорема 5. Пусть a и b – два целых числа, 



Этот способ называется алгоритмом Евклида. Задача нахождения НОД чисел a и b сводится к более простой задаче нахождения НОД b и r, 











Мы получим убывающую последовательность натуральных чисел
которая не может быть бесконечной. Поэтому существует остаток, равный нулю: пусть 

1. Решение неопределенных уравнений первой степени от двух переменных в целых числах
Рассмотрим два метода решения диофантовых уравнений первой степени от двух переменных.
Алгоритм этого метода рассмотрим на примере решения конкретного уравнения. Шаги алгоритма, которые необходимо применять при решении любого такого уравнения выделим курсивом.
Пример 1. Решить уравнение в целых числах 5x + 8y = 39.
1. Выберем неизвестное, имеющее наименьший коэффициент (в нашем случае это х), и выразим его через другое неизвестное: 
2. Выделим целую часть: 

3. Введем дополнительную целочисленную переменную z следующим образом: 4 –3y = 5z. В результате получим уравнение такого же типа, как и первоначальное, но уже с меньшими коэффициентами.
4. Решаем его уже относительно переменной y, рассуждая точно также как в п.1, 2: 
5. Рассуждая аналогично предыдущему, вводим новую переменную u: 3u = 1 – 2z.
6. Выразим неизвестную с наименьшим коэффициентом, в этом случае переменную z: 


7. Теперь необходимо «подняться вверх». Выразим через переменную v сначала z, потом y и затем x:
z = 





8. Формулы x = 3+8v и y = 3 – 5v, где v – произвольное целое число, представляют общее решение исходного уравнения в целых числах.
Замечание. Таким образом, метод спуска предполагает сначала последовательное выражение одной переменой чрез другую, пока в представлении переменной не останется дробей, а затем, последовательное «восхождение» по цепочке равенств для получения общего решения уравнения.
Это уравнение и любое другое линейное уравнение с двумя неизвестными может быть решено и другим методом, с использованием алгоритма Евклида, более того можно доказать, что уравнение, рассмотренное выше всегда имеет единственное решение. Приведем здесь формулировки теорем, на основании которых может быть составлен алгоритм решения неопределенных уравнений первой степени от двух переменных в целых числах.
Теорема 1.1. Если в уравнении 

Теорема 2.2. Если в уравнении 


Теорема 3.3. Если в уравнении 




Теорема 4.4. Если в уравнении 

где х0, у0 – целое решение уравнения 

Как уже отмечалось выше, сформулированные теоремы позволяют составить следующий алгоритм решения в целых числах уравнения вида 
1. Найти наибольший общий делитель чисел a и b,
если 

если 

2. Разделить почленно уравнение 



3. Найти целое решение (х0, у0) уравнения 


4. Составить общую формулу целых решений данного уравнения
где х0, у0 – целое решение уравнения 

Пример 2. Решить уравнение в целых числах 407х – 2816y = 33.
Воспользуемся составленным алгоритмом.
1. Используя алгоритм Евклида, найдем наибольший общий делитель чисел 407 и 2816:
2816 = 407·6 + 374;
33 = 11·3. Следовательно (407,2816) = 11, причем 33 делится на 11
2. Разделим обе части первоначального уравнения на 11, получим уравнение 37х – 256y = 3, причем (37, 256) = 1
3. С помощью алгоритма Евклида найдем линейное представление числа 1 через числа 37 и 256.
Выразим 1 из последнего равенства, затем, последовательно поднимаясь по цепочке равенств, будем выражать 3; 34 и полученные выражения подставим в выражение для 1.
1 = 34 – 3·11 = 34 – (37 – 34·1) ·11 = 34·12 – 37·11 = (256 – 37·6) ·12 – 37·11 =
– 83·37 – 256·(–12). Таким образом, 37·(– 83) – 256·(–12) = 1, следовательно пара чисел х0 = – 83 и у0 = – 12 есть решение уравнения 37х – 256y = 3.
4. Запишем общие формулы решений первоначального уравнения
где t — любое целое число.
Замечание. Можно доказать, что если пара (х1,y1) — целое решение уравнения 


2. Методы решения некоторых нелинейных диофантовых уравнений
Общие подходы к решению нелинейных диофантовых уравнений достаточно сложны и предполагают серьезную подготовку по теории чисел. Мы рассмотрим здесь некоторые уравнения и элементарные методы их решения.
Метод разложения на множители
Первоначальное уравнение путем группировки слагаемых и вынесения общих множителей приводится к виду, когда в левой части уравнения стоит произведение сомножителей, содержащих неизвестные, а справа стоит некоторое число. Рассматриваются все делители числа, стоящего в правой части уравнения. Проводится исследование, в котором каждый сомножитель, стоящий в правой части уравнения приравнивается к соответствующему делителю числа, стоящего в правой части уравнения.
Пример 3. Решить уравнение в целых числах y3 — x3 = 91.
Решение. 1) Используя формулы сокращенного умножения, разложим правую часть уравнения на множители:
2) Выпишем все делители числа 91: ± 1; ± 7; ± 13; ± 91
3) Проводим исследование. Заметим, что для любых целых x и y число
следовательно, оба сомножителя в левой части уравнения должны быть положительными. Тогда уравнение (1) равносильно совокупности систем уравнений:



4) Решив системы, получим: первая система имеет решения (5; 6), (-6; -5); третья (-3; 4),(-4;3); вторая и четвертая решений в целых числах не имеют.
Ответ: уравнение (1) имеет четыре решения (5; 6); (-6; -5); (-3; 4); (-4;3).
Пример 4. Решить в целых числах уравнение x + y = xy.
Решение. 1) Перенесем все члены уравнения влево и к обеим частям полученного уравнения прибавим (–1): x + y – xy – 1 = – 1
Сгруппируем первое – четвертое и второе – третье слагаемые и вынесем общие множители, в результате получим уравнение: (x — 1)(y — 1) = 1
2) Произведение двух целых чисел может равняться 1 в том и только в том случае, когда оба этих числа равны или 1, или (–1).
3) Записав соответствующие системы уравнений и решив их, получим решение исходного уравнения. Ответ: (0,0) и (2,2).
Пример 5. Доказать, что уравнение (x — y)3 + (y — z)3 + (z — x)3 = 30 не имеет решений в целых числах.
Решение. 1) Разложим левую часть уравнения на множители и обе части уравнения разделим на 3, в результате получим уравнение:
2) Делителями 10 являются числа ±1, ±2, ±5, ±10. Заметим также, что сумма сомножителей левой части уравнения (2) равна 0. Нетрудно проверить, что сумма любых трех чисел из множества делителей числа 10, дающих в произведении 10, не будет равняться 0. Следовательно, исходное уравнение не имеет решений в целых числах.
Метод испытания остатков
Этот метод основан на исследовании возможных остатков левой и правой частей уравнения от деления на некоторое фиксированное натуральное число.
Рассмотрим примеры, которые раскрывают сущность данного метода.
Пример 6. Решить в целых числах уравнение x2 + 1 = 3y.
Решение. 1) Заметим, что правая часть уравнения делится на 3 при любом целом y.
2) Исследуем какие остатки может иметь при делении на три левая часть этого уравнения.
По теореме о делении с остатком целое число х либо делится на 3, либо при делении на три в остатке дает 1 или 2.
Если х = 3k, то правая часть уравнения на 3 не делится.
Если х = 3k+1, то x2 + 1= (3k+1)2+1=3m+2, следовательно, опять левая часть на 3 не делится.
Если х = 3k+2, то x2 + 1= (3k+2)2+1=3m+2, следовательно, и в этом случае левая часть уравнения на три не делится.
Таким образом, мы получили, что ни при каких целых х левая часть уравнения на 3 не делится, притом, что левая часть уравнения делится на три при любых значениях переменной y. Следовательно, уравнение в целых числах решений не имеет.
Пример 7. Решить в целых числах x³ — 3y³ — 9z³ = 0.
Решение. 1) Очевидно, что решением уравнения будет тройка чисел (0; 0; 0).
2) Выясним, имеет ли уравнение другие решения. Для этого преобразуем уравнение к виду
Так как правая часть полученного уравнения делится на 3, то и левая обязана делится на три, следовательно, так как 3 — число простое, х делится на 3, т. е. х = 3k, подставим это выражение в уравнение (3): 27k3 = 3y³ + 9z³, откуда
следовательно, y³ делится на 3 и y = 3m. Подставим полученное выражение в уравнение (4): 9k3 = 27m³ + 3z³, откуда
В свою очередь, из этого уравнения следует, что z3 делится на 3, и z = 3n. Подставив это выражение в (5), получим, что k3 должно делиться на 3.
Итак, оказалось, что числа, удовлетворяющие первоначальному уравнению, кратны трём, и сколько раз мы не делили бы их на 3, опять должны получаться числа, кратные трём. Единственное целое число, удовлетворяющее этому условию, будет нуль, т. е. решение данного уравнения (0; 0; 0) является единственным.
Контрольное задание №1
Представленные ниже задачи являются контрольным заданием №1 для учащихся 9 классов. Решения необходимо оформить в отдельной тетради и выслать по адресу 8, ХКЦТТ, ХКЗФМШ. Для зачета нужно набрать не менее 15 баллов (каждая правильно решенная задача оценивается в 3 балла).
М.9.1.1. Решив задачу, помещенную вначале статьи, определить сколько лет прожил Диофант.
М.9.1.2. Решить уравнения в целых числах
М.9.1.3. Найдите день моего рождения, если сумма чисел равных произведению даты рождения на 12 и номера месяца рождения на 31 равна 380.
М.9.1.4. Кусок проволоки длиной 102 см нужно разрезать на части длиной 15 см и 12 см, так чтобы была использована вся проволока. Как это сделать?
М.9.1.5. Решить уравнения в целых числах
М.9.1.6. Докажите, что уравнение x2 – y2 = 30 не имеет решений в целых числах.
М.9.1.7. Существуют ли целые числа m и n, удовлетворяющие уравнению m2 + 1994 = n2
1. Башмакова, И. Г. Диофант и диофантовы уравнения. – М.: Наука, 1972.
2. Фоминых, Ю. Ф. Диофантовы уравнения //Математика в шк. – 1996. — №6.
3. Школьная энциклопедия. Математика. / под редакцией – М.: Издательство «Большая российская энциклопедия», 1996.
4. Бабинская, И. Л. Задачи математических олимпиад. – М., 1975.
5. Васильев, Н. Б. Задачи Всесоюзных математических олимпиад. – М., 1998.
6. Курляндчик, Л. Метод бесконечного спуска // Приложение к журналу «Квант». 1999. – №3.
7. Яковлев, Г. Н. Всесоюзные математические олимпиады школьников. М., 1992.
8. Серпинский, В. О решении уравнений в целых числах. – М, 1961.
9. Перельман, Я. И. Занимательная алгебра. – М.: Наука, 1975.
💡 Видео
РЕШАЕМ ДИОФАНТОВОЕ УРАВНЕНИЕ | ПРОСТЫМИ СЛОВАМИСкачать

Математика. Линейные диофантовы уравнения с двумя неизвестными. Центр онлайн-обучения «Фоксфорд»Скачать

ПЕРЕЧНЕВЫЕ ОЛИМПИАДЫ. Диофантовы уравненияСкачать

Как решать Диофантовы уравнения ➜ Решите уравнение в целых числах 4x+5y=6Скачать

Дробно-рациональные уравнения. 8 класс.Скачать

Рациональные уравнения. ОГЭ номер 21 | ЕГЭ номер 13 | Математика | TutorOnlineСкачать

Решение уравнений, 6 классСкачать

16. Решение линейных уравнений в целых числах. Часть 1. Алексей Савватеев. 100 уроков математикиСкачать

Схема Горнера. 10 класс.Скачать