Уравнение с суммой ряда онлайн (5 видео)

Содержание

Сумма ряда по-шагам
Результат
Примеры нахождения суммы ряда
Правила ввода
Вычислить сумму ряда онлайн
Другие полезные разделы:
Оставить свой комментарий:
Сходимость или расходимость ряда
📺 Видео

Видео:Математика без Ху!ни. Вычисление суммы рядаСкачать

Сумма ряда по-шагам

Видео:Найти сумму рядаСкачать

Результат

Примеры нахождения суммы ряда

Сумма степенного ряда
Факториал

Указанные выше примеры содержат также:

квадратные корни sqrt(x),
кубические корни cbrt(x)
тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x)
показательные функции и экспоненты exp(x)
обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс actan(x)
натуральные логарифмы ln(x),
десятичные логарифмы log(x)
гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x)
обратные гиперболические функции:
asinh(x), acosh(x), atanh(x), actanh(x)
число Пи pi
комплексное число i

Правила ввода

Можно делать следующие операции

2*x — умножение 3/x — деление x^3 — возведение в степень x + 7 — сложение x — 6 — вычитание Действительные числа вводить в виде 7.5, не 7,5

Чтобы увидеть подробное решение,
помогите рассказать об этом сайте:

Видео:1. Числовой ряд. Определение сходимости. Сумма ряда. #neliseeva #исследоватьрядСкачать

Вычислить сумму ряда онлайн

Для того, чтобы вычислить сумму ряда, нужно просто сложить элементы ряда заданное количество раз. Например:

В приведённом выше примере это удалось сделать очень просто, поскольку суммировать пришлось конечное число раз. Но что делать, если верхний предел суммирования бесконечность? Например, если нам нужно найти сумму вот такого ряда:

По аналогии с предыдущим примером, мы можем расписать эту сумму вот так:

Но что делать дальше?! На этом этапе необходимо ввести понятие частичной суммы ряда. Итак, частичной суммой ряда (обозначается S_n ) называется сумма первых n слагаемых ряда. Т.е. в нашем случае:

Тогда сумму исходного ряда можно вычислить как предел частичной суммы:

Таким образом, для вычисления суммы ряда, необходимо каким-либо способом найти выражение для частичной суммы ряда ( S_n ). В нашем конкретном случае ряд представляет собой убывающую геометрическую прогрессию со знаменателем 1/3. Как известно сумма первых n элементов геометрической прогрессии вычисляется по формуле:

здесь b ₁ — первый элемент геометрической прогрессии (в нашем случае это 1) и q — это знаменатель прогрессии (в нашем случае 1/3). Следовательно частичная сумма S_n для нашего ряда равна:

Тогда сумма нашего ряда ( S ) согласно определению, данному выше, равна:

Рассмотренные выше примеры являются достаточно простыми. Обычно вычислить сумму ряда гораздо сложнее и наибольшая трудность заключается именно в нахождении частичной суммы ряда. Представленный ниже онлайн калькулятор, созданный на основе системы Wolfram Alpha, позволяет вычислять сумму довольно сложных рядов. Более того, если калькулятор не смог найти сумму ряда, вероятно, что данный ряд является расходящимся (в этом случае калькулятор выводит сообщение типа «sum diverges»), т.е. данный калькулятор также косвенно помогает получить представление о сходимости рядов.

Для нахождения суммы Вашего ряда, необходимо указать переменную ряда, нижний и верхний пределы суммирования, а также выражение для n -ого слагаемого ряда (т.е. собственно выражение для самого ряда).

Видео:Математика без Ху!ни. Ряды. Часть 1. Сумма ряда. Сходимость. Геометрическая прогрессия.Скачать

Другие полезные разделы:

Видео:Сумма числового ряда n^2/2^nСкачать

Оставить свой комментарий:

Мы в социальных сетях:
Группа ВКонтакте | Бот в Телеграмме

Видео:Числовые ряды-3. Как находить сумму рядаСкачать

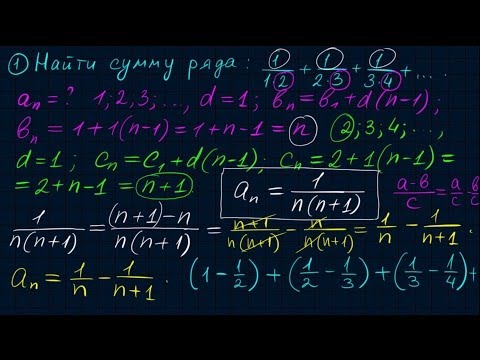
Сходимость или расходимость ряда

Данный калькулятор предназначен для исследования ряда на сходимость. Под числовым рядом понимается сумма членов числовой последовательности следующего вида: ∑ ∞ _n=1a_n=a₁+a₂+a₃+…, где все a — это числа. Если говорить о функциональном ряде, то все члены последовательности являются функциями: ∑ ∞ _n=1f_n(x)=f₁(x)+f₂(x)+f₃(x)+… Ряд, членами которого являются степенные функции, называется степенным рядом: ∑ ∞ _n=1a_nx n . Чтобы найти сходимость числового ряда, функционального ряда или степенного ряда, необходимо знать признаки сходимости рядов. Существует необходимый признак сходимости ряда: если ряд ∑ ∞ _n=1a_n сходится, то (lim)┬(n→∞)⁡an=0.

Однако данный признак не является гарантией сходимости ряда, поэтому рассматриваются также достаточные признаки сходимости. Признаки сравнения рядов заключаются в следующем. Даны два ряда ∑ ∞ _n=1a_n и ∑ ∞ _n=1b_n, при этом 0 ∞ _n=1b_n сходится, то также должен сходиться ряд ∑ ∞ _n=1a_n. Если ∑ ∞ _n=1a_n расходится, то ∑ ∞ _n=1b_n тоже расходится. Предельные признаки сравнения рядов состоят в следующем. Даны два ряда ∑ ∞ _n=1a_n и ∑ ∞ _n=1b_n, при этом a_n и b_n – положительны. Тогда, во-первых, если 0 ∞ _n=1a_n сходится, если сходится ∑ ∞ _n=1b_n. В-третьих, если lim a_n/b_n=∞, то ∑ ∞ _n=1a_n расходится, если расходится ∑ ∞ _n=1b_n. Калькулятор поможет определить сходимость или расходимость ряда онлайн. Расшифровка ответов следующая: Для получения полного хода решения нажимаем в ответе Step-by-step.