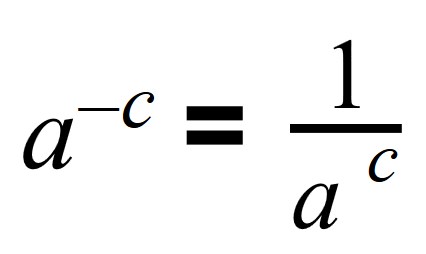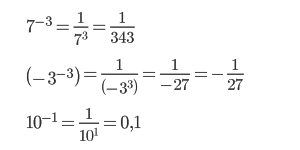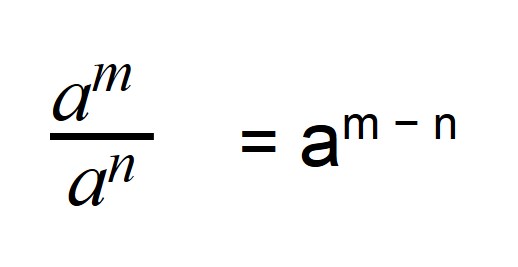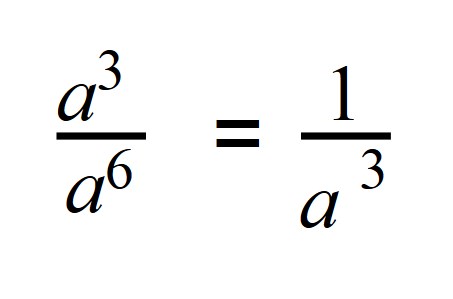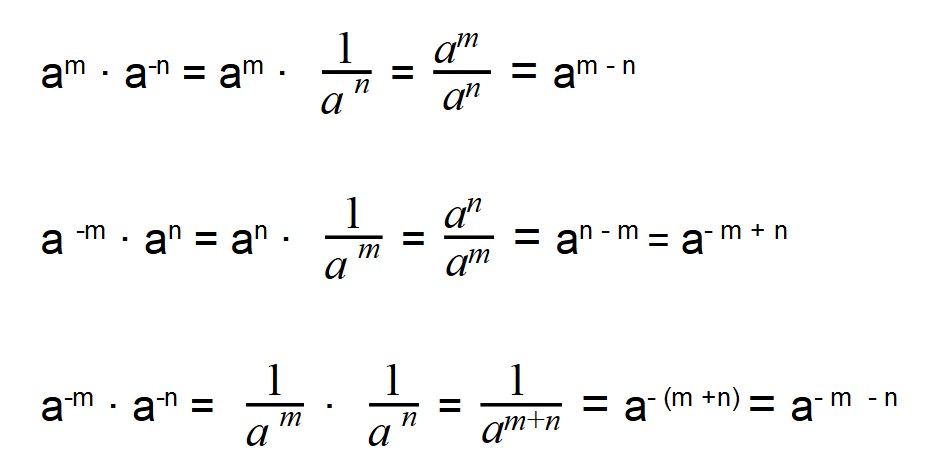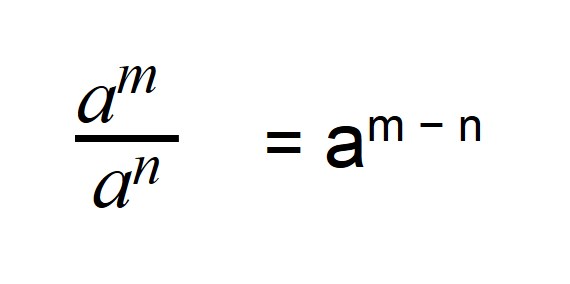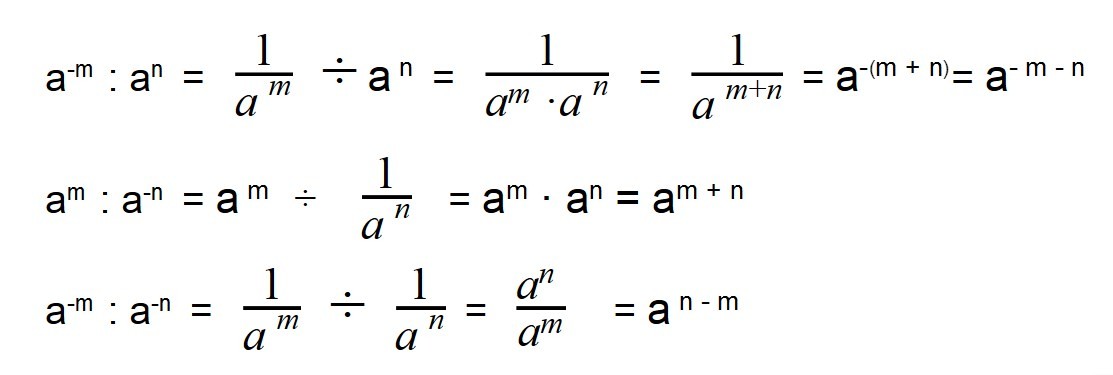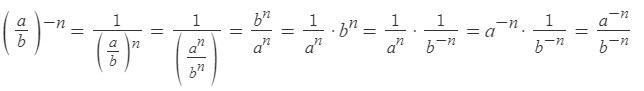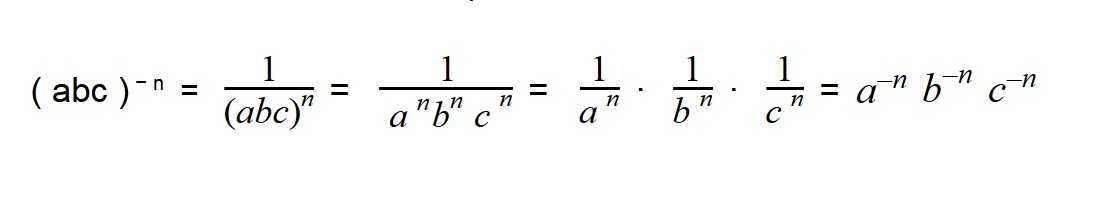Уравнение с отрицательными степенями как решать онлайн (6 видео)

Отрицательная степень

О чем эта статья:

7 класс, 8 класс

Содержание

Что такое степень числа
Степень с отрицательным показателем
Действия с отрицательными степенями
Умножение отрицательных степеней
Деление отрицательных степеней
Возведение дроби в отрицательную степень
Возведение произведения в отрицательную степень
Уравнение с отрицательными степенями как решать онлайн
Решить уравнение со степенями онлайн
Калькулятор
Инструкция
Уравнение со степенями
📽️ Видео

Видео:Решение уравнений с отрицательными числами.Скачать

Что такое степень числа

В учебниках по математике можно встретить такое определение:

«Степенью n числа а является произведение множителей величиной а n раз подряд»

Например, a n — степень, где:

a — основание степени,
n — показатель степени.

Читается такое выражение как a в степени n.

Если говорить проще, то степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить данное число (основание степени) само на себя.

А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число 2 в третью степень, то она решается довольно просто:

2 3 = 2 · 2 · 2, где:

2 — основание степени,
3 — показатель степени.

Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.

Видео:Отрицательная степень числа - Разбор задания из ОГЭСкачать

Степень с отрицательным показателем

Число в минусовой степени равно дроби, числителем которой является единица, а знаменателем данное число с положительным показателем:

К примеру, 4 в минус 2 степени — это 1/4 2 , 2 в минус 3 степени — это 1/2 3 , 3 в минус 1 степени — это 1/3, 10 в минус первой степени — это 1/10 или 0,1.

Степени с отрицательным показателям помогают компактно записывать крайне малые или постоянно уменьшающиеся величины. Например, одну миллиардную долю (0, 000 000 001) можно записать как 10 в минус 9 степени (10 -9 ). В школьной программе такие величины — редкость: чаще всего используют 10 в минус 1 степени или 2 в минус 1 степени.

Чтобы разобраться, как возводить число в отрицательную степень, вспомним правило деления степеней с одинаковыми основаниями.

Деление степеней с одинаковыми основаниями, но разными показателями осуществляется по следующей формуле: показатели отнимаются, а основание остается неизменным.

Поэтому если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью:

a 3 : a 6 =a 3 — 6 = a -3

Если записать деление в виде дроби, то при сокращении в числителе останется 1, а в знаменателе число будет иметь положительную степень:

Видео:8 класс, 6 урок, Степень с целым отрицательным показателемСкачать

Действия с отрицательными степенями

Умножение отрицательных степеней

При умножении отрицательных степеней с одинаковыми основаниями показатели степеней складываются, так же как и при умножении положительных степеней:

a m · a n = a m + n

Деление отрицательных степеней

При делении отрицательных степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель делителя, так же как и при делении положительных степеней:

Возведение дроби в отрицательную степень

Чтобы возвести дробь в отрицательную степень, надо возвести в эту степень отдельно числитель и знаменатель:

Возведение произведения в отрицательную степень

Чтобы возвести произведение в отрицательную степень, необходимо возвести в эту степень каждый множитель произведения отдельно:

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Уравнение с отрицательными степенями как решать онлайн

Запись a n означает что число a должно быть умножено n раз:

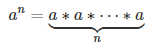
Пример 1. 5 3 =5*5*5=125

Деление это обратная операция умножению. Отрицательная степень означает сколько раз нужно разделить число.

Число в отрицательной степени a -n может быть записано в виде:

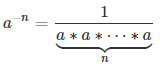
Пример 2 может быть записан в виде.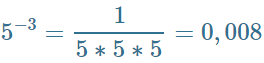

Уравнение с отрицательными степенями как решать онлайн

Определение. Если a≠0 и n — целое отрицательное число, то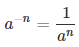

Для вычисления числа a -n в отрицательной степени нужно:

1.Вычислить a n

2.Затем разделить 1 на полученный результат, т.е.

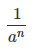
Воспользуйтесь калькулятором для вычисления числа в отрицательной степени.

Видео:Решение уравнений, 6 классСкачать

Решить уравнение со степенями онлайн

Калькулятор поможет вам решить уравнения, где есть любые степени. Всё что нужно – это ввести нужные значения и вы получите довольно-таки развёрнутое решение. В дальнейшем вы сможете решать такие уравнения без помощи калькулятора.

Видео:Математика| СтепениСкачать

Калькулятор

Видео:КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

Инструкция

Примечание: π записывается как pi; корень квадратный как sqrt().

Шаг 1. Введите заданное уравнение в поле.

Шаг 2. Нажмите кнопку “Решить”.

Шаг 3. Получите развёрнутый ответ.

Вводить можно любые цифры при помощи клавиатуры. А чтобы показать степень, применяется знак – ^.

Видео:Степень с целым показателем. 7 класс.Скачать

Уравнение со степенями

Уравнение со степенями – это уравнение, в котором над число стоит определённая степень. Если у вас квадратное уравнение, его можно решить через дискриминант. Чем больше степеней в уравнении, тем сложнее оно решается. Однако, так кажется только на первый взгляд. Кубическое уравнение можно решать по формуле Виета. Калькулятор справится с этими уравнениями быстро и легко.

Средняя оценка 1.7 / 5. Количество оценок: 16