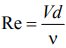Уравнение рейнольдса в полярных координатах (7 видео)

Уравнения Рейнольдса

Содержание

Уравнения Рейнольдса
Формула числа Рейнольдса Re
Калькулятор для расчета Re онлайн
Расчет по общей формуле
Расчет Re для воды
Расчет Re для воздуха
Формула
Физический смысл
Режимы течения
Критическое значение
Размерность
Течение в трубе
Число Рейнольдса
Опыты Рейнольдса
Вывод формулы
Число Рейнольдса и режимы течения.
🔍 Видео

Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Уравнения Рейнольдса

Уравнения Рейнольдса. Как уже отмечалось, турбулентное движение жидкости характеризуется случайными хаотическими случайными изменениями скорости и других гидродинамических параметров. Поскольку эти изменения носят характер нерегулярных пульсаций, поля гидродинамических параметров могут быть выражены как сумма усредненных полей параметров и 2 полей пульсаций параметров. Используя это представление, запишите фактические локальные предсказания скорости-их среднее u«, «те U2 и пульсирующая добавка по, давление р = р + р ’будет делать то же самое. Так… С учетом пульсационной составляющей среднего времени 7.

Метод осреднения Рейнольдса заключается в замене случайно изменяющихся характеристик потока (скорость, давление, плотность) суммами осреднённых и пульсационных составляющих. Людмила Фирмаль

Локальная скорость и давление равны нулю: их-0; их= * 0; ig = 0; пульсирующая составляющая равна p ’= 0, поскольку вероятность как положительных, так и отрицательных значений является равной знакопеременной величиной. Рейнольдс предложил следовать определенным правилам после усреднения. Если /и p-средние зависимые переменные, а a-любая из 4 независимых переменных x, y, r, то/ = /; д] 7 *（* _ / + P = / + P; / p = / p;= -; I / Людмила Фирмаль

Турбулентное тангенциальное напряжение выражается в виде tturb, Е = Р»

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Видео:Полярная система координатСкачать

Формула числа Рейнольдса Re

Видео:§30 Уравнения кривых второго порядка в полярных координатахСкачать

Калькулятор для расчета Re онлайн

Расчет по общей формуле

Расчет Re для воды

Расчет Re для воздуха

Видео:Построение кривой в полярной системе координатСкачать

Формула

Расчетная формула числа Рейнольдса Re в общем виде:

где — плотность среды, кг/м 3 ; — характерная скорость, м/с; — гидравлический диаметр, м; — динамическая вязкость среды, Па·с или кг/(м·с); — кинематическая вязкость среды ( ), м 2 /с; — объёмный расход потока, м 3 /с; — площадь сечения канала, например, трубы, м 2 .

Для труб круглого сечения расчетная формула числа Рейнольдса Re будет:

V — характерная скорость, м/с;
d — внутренний диаметр трубы, м;
— кинематическая вязкость среды ( ), м 2 /с;

Видео:Оператор Лапласа в полярных координатахСкачать

Физический смысл

Физический смысл – число Рейнольдса Re характеризует смену режимов течения от ламинарного к турбулентному. Re является критерием подобия течения вязкой жидкости.

Критерий назван в честь выдающегося английского физика Осборна Рейнольдса (1842—1912).

В настоящее время не существует строгого научно доказанного объяснения этому явлению, однако наиболее достоверной гипотезой считается следующая: смена режимов движения жидкости определяется отношением сил инерции к силам вязкости в потоке жидкости. Если преобладают первые, то режим движения турбулентный, если вторые – ламинарный.

Видео:Скорость и ускорение точки в полярных координатахСкачать

Режимы течения

Режим течения в динамическом пограничном слое зависит от числа Рейнольдса Re и может быть:

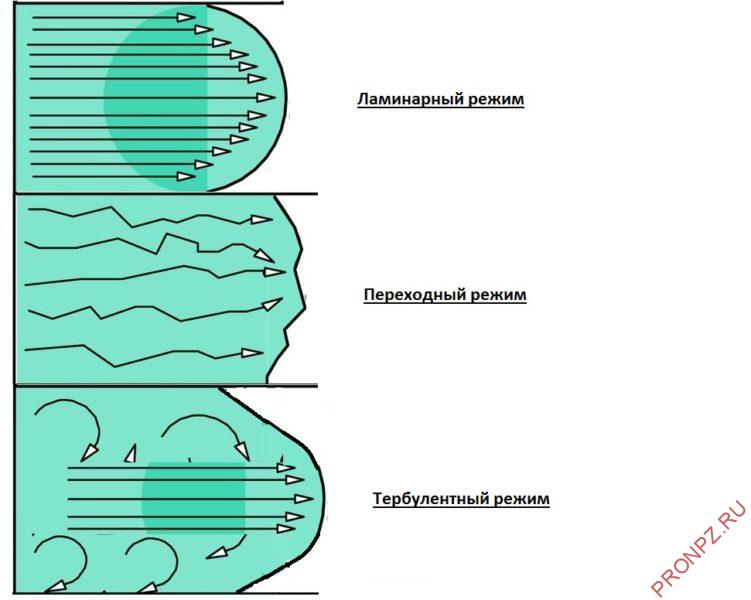
Ламинарный режим – слоистое течение без перемешивания частиц жидкости и без пульсации скорости и давления, все линии тока направлены параллельно.
Турбулентный режим – течение, сопровождающееся интенсивным перемешиванием жидкости с пульсациями скоростей и давлений, наряду с основным продольным перемещением жидкости наблюдаются поперечные перемещения и вращательные движения отдельных объемов жидкости.

Эпюры скоростей

Видео:Видеоурок "Полярная система координат"Скачать

Критическое значение

Переход к турбулентному режиму течения жидкости в пограничном слое определяется критическим значением числа Рейнольдса. Это обусловлено тем, что при возрастании скорости, участвующей в расчете числа Re, его значение растет.
Таким образом, переход от ламинарного режима к турбулентному наблюдается при определенной скорости движения жидкости. Эта скорость называется критической Vкр.

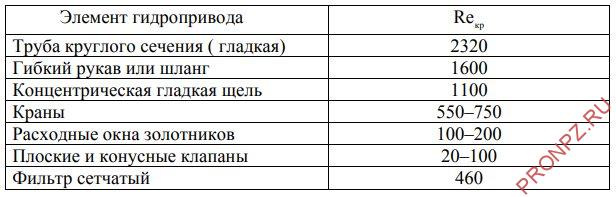
Значение критического числа Re для различных элементов гидропривода

Видео:Площадь фигуры через двойной интеграл в полярных координатахСкачать

Размерность

Числе Re не имеет единиц измерения. Re является безразмерным критерием подобия течения вязкой жидкости.

Видео:Двойной интеграл в полярных координатахСкачать

Течение в трубе

При ламинарном течении жидкости в прямой трубе или канале постоянного сечения все линии тока направлены параллельно оси трубы, при этом отсутствуют поперечные перемещения частиц жидкости.

При турбулентном течении в канале наряду с основным продольным перемещением жидкости в трубе наблюдаются поперечные перемещения и вращательные движения отдельных объемов жидкости.

Зависимость режима течения от значения числа Re в гладких трубах:

2300 – Турбулентный режим

Обычно предполагается, что при числе Re выше 2300 образуется турбулентный режим.

Тем не менее, при значениях Re выше критического и до определённого предела наблюдается переходной (смешанный) режим течения жидкости, когда турбулентное течение более вероятно, но ламинарное в некоторых конкретных случаях тоже наблюдается — так называемая неустойчивая турбулентность. В трубах такой переходный интервал может достигать вплоть до Re = 2300—10 000.

Видео:Полярные координаты. Полярное уравнение эллипса.Скачать

Число Рейнольдса

Движение жидкости, несмотря на кажущуюся на первый взгляд, беспорядочность движения имеет определенные закономерности. Рейнольдс в своих опытах нашел определенные общие условия, при которых возможно существование того или иного режима течения и переход от одного режима к другому.

При проведении опытов Рейнольдс в 1883г. подтвердил существование двух режимов течения жидкости. Ему удалось вычислить безразмерное число, описывающее характер потока вязкой жидкости

Содержание статьи

Видео:Построение графика функции в полярных координатахСкачать

Опыты Рейнольдса

Эксперименты О.Рейнольдса показали, что при движении жидкости , последняя теряет определенное количество энергии. Эти потери зависят от особенностей движения частиц жидкости в потоке и от самого режима течения.

Опыты проводились на специальном лабораторном стенде, который представлял собой заполненный водой бак Б к которому в нижней части присоединена стеклянная трубка Т. На конце трубки установлен кран К для регулирования расхода жидкости. Расход измеряется с помощью секундомера и мерного бочка М. Бак Б постоянно заполняется водой. Над баком Б расположена ёмкость с краской С. По тонкой трубочке Т1 краска попадает в жидкость, движущуюся в трубке Т. Подачу краски регулирует кран Р.

Опыт №1. Немного приоткрываем кран К. При этом в трубке Т начинается движение жидкости. Открываем кран Р и добавляем в жидкость краску. При небольшой скорости движения в трубке Т краска становится прямолинейной и резко выделяющейся в потоке воды цветной струйкой. Эта струйка не перемешивается с остальной жидкостью. Если ввести в жидкость краску несколькими струйками, то они так и будут двигаться не перемешиваясь с остальной водой.

Движение жидкости, наблюдаемое при малых скоростях, при котором отдельные струйки жидкости движутся параллельно друг другу и оси потока, называют ламинарным (от латинского ламина — слой) или струйчатым движением (режимом). Ламинарное движение может рассматриваться как движение отдельных слоев жидкости, происходящее без перемешивания частиц. Подробнее о ламинарном режиме здесь.

Опыт №2 При намного большем открытии крана струйка краски начинает искривляться и становится волнообразной. Открывая кран ещё больше и увеличивая скорость потока мы увидим, что струйка краски распадается на отдельные вихри и перемешивается с остальной массой воды

Движение жидкости, которое наблюдается при больших скоростях, называется турбулентным (по латински турбулентус — вихревой) движением (режимом). В этом случае в движении жидкости нет видимой закономерности. Отдельные частицы перемешиваются между собой и движутся по самым причудливым, все время меняющимся траекториям весьма сложной формы. Поэтому такое движение называется беспорядочным. Подробнее о турбулентном режиме здесь.

Вывод формулы

Рейнольдс установил, что основными факторами, определяющими характер режима являются:
средняя скорость движения жидкости υ,
диаметр трубопровода d,
плотность жидкости ρ,
абсолютная вязкость жидкости μ

При этом чем больше размеры поперечного сечения и плотность жидкости и чем меньше её вязкость, тем легче при увеличении скорости осуществить турбулентный режим.

Для характеристики режима движения жидкости Рейнольдсом был выведен безразмерный параметр Re, учитывающий влияние перечисленных выше факторов, называемый число Рейнольдса. Таким образом формула

Поскольку μ / ρ = ν , где ν – кинематическая вязкость жидкости, то формула меняет вид на

Число Рейнольдса и режимы течения.

Границы существования того или иного режима движения жидкости определяются двумя критическими значениями числа Рейнольдса:
нижнее критическое числом Рейнольдса Re_{кр. н.}
верхнее критическое числом Рейнольдса Re_{кр. в.}

Значение скорости, соответствующее этим значениям Re называют критическими.

При значениях числа Рейнольдса Re Re_{кр. в.} – только турбулентный. При Re_{кр. н.} 2300 – всегда турбулентный режимы.

При этом движении жидкости в неустойчивой зоне исключается из особого рассмотрения, это приводит к некоторому запасу и большей надежности в гидравлических расчетах в случае, если в этой зоне действительно имеет место ламинарный режим.

Без особого труда можно получить значения для Reкр для любой формы сечения, а не только круглой формы. Вспоминая, что при круглом сечении радиус

подставляем в формулу для определения числа Рейнольдса

Принимая для критического числа Рейнольдса независимо от формы живого сечения величину Re_кр. = 2300, находим, что для сечения любой формы критериев для сужения о характере режима движения является величина, равная 2300 / 4 = 575.

Таким образом, режим ламинарный если значение числа Рейнольдса

И режим турбулентный, если

Видео по теме.

На практике в большинстве случаев (движение воды в трубах, каналах, реках) приходится иметь дело с турбулентным режимом. Ламинарный режим встречается реже. Он наблюдается, например, при движении в трубах очень вязких жидкостей, что иногда имеет место в нефтепроводах, при движении жидкости в очень узких трубках и порах естественных грунтов.