Уравнение рэлея и его практическое применение (7 видео)

Содержание

Закон Релея, его анализ, границы применимости
РАССЕЯНИЕ СВЕТА, УРАВНЕНИЕ РЭЛЕЯ И ЕГО АНАЛИЗ
2.4. Оптические свойства коллоидных систем 2.4.1. Рассеяние света в золях
🎬 Видео

Видео:Закон БернуллиСкачать

Закон Релея, его анализ, границы применимости

Рассеяние света.

Светорассеяние наблюдается как в коллоидных, так и грубодисперсных системах. Однако механизм его различен для этих систем и зависит от размера частиц дисперсной фазы.

В грубодисперсных системах, частицы которых больше длины волны падающего на них света, светорассеяние вызывается 3 причинами:

I) отражением света от наружных поверхностей частиц;

2) преломлением света;

3) полным внутренним отражением.

Последние две причины имеют место в случае прозрачности вещества дисперсной фазы.

Вследствие хаотичности расположения частиц в таких системах свет рассеивается тоже хаотично и в общем итоге равномерно по всем направлениям. При этом лучи разной длины волны рассеиваются одинаково: если падающий свет белый, то и рассеянный свет белый. Такой вид рассеяния обусловливает мутность суспензий и эмульсий как в проходящем, так и в отраженном (боковом) свете.

В коллоидных системах размеры частиц меньше длины волны падшего на них света. Поэтому световые лучи не могут отражаться от таких частиц. Эта основная причина того, что коллоидные частицы невидимы даже в самые сильные микроскопы.

Светорассеяние в коллоидных системах вызвано явлением дифракции, которое заключается в том, что лучи света огибают коллоидные частицы и изменяют свое направление, рассеиваясь во все стороны.

Таким образом, как бы каждая частица становится источником новых — вторичных — волн. Именно этот вид светорассеяния и обусловливает явления опалесценции и эффект Фарадея-Тиндаля в золях.

Если светорассеяние в коллоидных системах сопровождается изменением окраски золя в отраженном свете по сравнению с его окраской в проходящем свете, то его принято называть опалесценцией (от слова опал — названия известного минерала, камня-самоцвета с молочным отливом). При этом окраска в отраженном свете сдвинута в сторону более коротких волн. Например, белые золи (золь канифоли, золь иодида серебра) опалесцирует голубым светом.

Эффект Фарадея-Тиндаля отличается от опалесценции только способом наблюдения. Эффект Фарадея-Тиндаля также обусловлен рассеянием света путем дифракции его в коллоидных системах. Этот эффект заключается в появлении светящегося конуса (или светящейся полосы) при прохождении пучка света через жидкие или газообразные золи при наблюдении сбоку на темном фоне. Фарадей наблюдал его впервые в 1857 году в золях золота. Позднее, в 1868 году Тиндаль исследовал это явление более подробно не только для жидких, но и для газовых систем.

В истинных растворах, молекулярных смесях и чистых жидкостях эффект Фаредея-Тиндаля не наблюдается. Следовательно, эффект Фарадея-Тиндаля является важным средством для решения вопроса о том, относится ли данная система к коллоидной.

Закон Релея, его анализ, границы применимости.

Зависимость интенсивности света, рассеянного в результате дифракции светового луча от внешних и внутренних факторов системы выражается формулой Релея (1871 г.):

где — интенсивность рассеянного света;

— интенсивность падающего света;

n — число частиц в единице объема;

υ — объем каждой частицы;

λ — длина волны падающего света;

α — угол между направлениями падающего и рассеянного света;

x — расстояние от частицы до наблюдателя;

— показатель преломления дисперсной фазы;

— показатель преломления дисперсионной среды.

При постоянных x и α из уравнения (I) вытекает следующее:

Интенсивность рассеянного света:

1) прямо пропорциональна интенсивности падающего света, концентрации золя и квадрату объема отдельных частиц;

2) обратно пропорциональна четвертой степени длины волны падающего света;

3) находится в прямой зависимости от разности между показателями преломления дисперсной и дисперсионной фаз.

Уравнение (I) можно упростить, если принять, что x=Const; α=90°; Sin90°=1

Тогда (2)

Формула (2) имеет большое значение, так как она лежит в основе оптических методов исследования дисперсных систем.

Проанализируем формулу Релея и посмотрим какие из нее можно сделать выводы.

1. Допустим мы имеем два золя с одинаковой дисперсной фазой
и дисперсионной средой, с одной и той же весовой концентрацией,
но с разной степенью дисперсности частиц. и λ примем постоянными. Тогда согласно уравнению (2) можно записать:

(3)

Так как где С — весовая концентрация.

Таким образом, интенсивность рассеяния прямо пропорциональна кубу радиуса частицы, или обратно пропорциональна кубу степени дисперсности D.

То есть степень дисперсности играет решающую роль в светорассеивании. Например, повышение D в 10 раз должно понизить светорассеивание в 1000раз.

2. Допустим, мы имеем два золя с одинаковой дисперсной фазой
и дисперсионной средой, с одной и той же степенью дисперсности .

Тогда (4)

То есть наибольшее рассеяние будет давать свет с наиболее короткими волнами. Например, интенсивность рассеяния синего цвета (λ=440 нм) больше интенсивности рассеяния красного света (λ = 660 нм) примерно в 5 раз.

Понятно, почему при падающем белом свете золь опалесцирует синим цветом, а при монохроматическом свете – только данным цветом.

3. Примем величины , r и λ постоянными, значения показателей преломления и будут различными. Тогда решающим фактором при рассеянии является разность — .

Чем больше эта разность, тем больше светорассеяние.

Видео:Как выучить Химию с нуля за 10 минут? Принцип Ле-ШательеСкачать

РАССЕЯНИЕ СВЕТА, УРАВНЕНИЕ РЭЛЕЯ И ЕГО АНАЛИЗ

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ

Гетерогенность дисперсных систем является причиной их оптической неоднородности и вызывает изменение направления световых, электронных, ионных и других лучей на межфазных поверхностях, а также неодинаковое поглощение или пропускание лучей веществами сопряженных фаз дисперсной системы. Всё это является причиной появления целого ряда специфических оптических явлений, присущих только коллоидным системам. Отличие оптических свойств коллоидных систем от свойств однородных сред привело к созданию целого ряда оптических методов исследования дисперсных систем, которые широко используются для изучения состава и структуры фаз, свойств межфазных поверхностей, дисперсности системы, а также природы, состава и структуры поверхностных слоёв.

Теоретические основы оптических явлений, характерных для дисперсных систем, и оптические методы их исследования следует изучить по учебникам, перечень которых приведен в списке литературы. В данном методическом пособии даётся только краткое теоретическое введение.

Основная часть издания посвящена практической части раздела «оптические свойства дисперсных систем» курса коллоидной химии и содержит подробное описание лабораторной работы по теме с практическими рекомендациями по её выполнению, обработке полученных данных и составлению отчета. Перед началом работы необходимо прочитать и принять к неукоснительному исполнению правила по технике безопасности, которые приведены в начале описания лабораторной работы и являются дополнением к общему инструктажу, проводимому со студентами в начале семестра.

Освоение практической части следует начинать только после изучения теории. Для теоретической подготовки по теме ниже приводится план теоретического коллоквиума. В конце методического пособия приведено приложение, которое является вспомогательным материалом, полезным для самоконтроля: контрольные вопросы и задачи.

ПЛАН ТЕОРЕТИЧЕСКОГО КОЛЛОКВИУМА

1. Общая характеристика оптических явлений.

2. Явление рассеяния света. Эффект Тиндаля. Влияние размеров частиц на вид индикатриссы рассеяния (диаграмма Ми).

3. Уравнение Рэлея и его анализ.

4. Светорассеяние токопроводящими сферическими частицами.

5. Абсорбция света. Уравнение Бугера – Ламберта — Бера. Оптическая плотность раствора, светопропускание, относительное поглощение.

6. Оптические методы исследования коллоидных систем: (принципиальные основы метода, его возможности и границы применимости):

а) световая и электронная микроскопия;

г) нефелометрия; определение молярной массы макромолекул.

7. Окраска коллоидных систем.

8. Лабораторная работа. Определение размеров частиц дисперсных систем турбидиметрическим методом:

a) Принципиальная оптическая схема фотоэлектроколориметра;

б) Определение размеров частиц дисперсных систем, подчиняющихся уравнению Рэлея;

в) Определение размеров частиц дисперсных систем, не подчиняющихся уравнению Рэлея, метод Геллера.

9. Самоподготовка по контрольным вопросам и задачам в приложении.

СПИСОК ЛИТЕРАТУРЫ

1. Фролов Ю.Г. Курс коллоидной химии. М., Химия, 1982г., с.245-267.

2. Боюцкий С.С. Курс коллоидной химии. М., Химия, 1975г., с. 33-53

3. Фридрихсберг Д.А. Курс коллоидной химии. Л., Химия, 1984г., с.38-44.

4. Лабораторные работы и задачи по коллоидной химии.- Под. ред. Ю.Г. Фролова и А.С. Гродского. М., Химия, 1986г., с.111-117.

5. Расчёты и задачи по коллоидной химии. Под ред. В.И.Барановой. М., Высш. шк., с. 254-260.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

РАССЕЯНИЕ СВЕТА, УРАВНЕНИЕ РЭЛЕЯ И ЕГО АНАЛИЗ

При падении луча света на дисперсную систему возможно его прохождение или преломление, а также отражение, рассеяние или поглощение света частицами дисперсной фазы. Прохождение света характерно для прозрачных гомогенных сред. Отражение – для микрогетерогенных и грубодисперсных систем с размерами частиц, превышающими длину волны падающего света (0,4 — 0,7 мкм), и проявляется в виде мутности суспензий, эмульсий и аэрозолей. Для коллоидных систем с радиусом частиц меньше длины волны падающего света характерны явления рассеяния света (опалесценция) и его поглощение (абсорбция).

Теория светорассеяния для сферических частиц, не проводящих электрический ток, разработана Рэлеем.

Дисперсные системы с размерами частиц, меньше длины световой волны, рассеивают свет во всех направлениях. При этом каждая точка неоднородности становится источником вторичных электромагнитных колебаний с частотой, равной частоте волны падающего света (дифракция). Частица представляет собой, таким образом, наведенный диполь, равный произведению поляризуемости частицы α на напряженность электрического поля Е:

Интенсивность рассеянного света определяется величинами, входящими в уравнение (1). Поляризуемость частицы α пропорциональна её объёму V, а интенсивность рассеяния света пропорциональна квадрату поляризуемости и, следовательно, квадрату объёма частицы. Таким образом, с ростом размера частиц интенсивность рассеяния возрастает. На поляризуемость влияет также разность показателей преломления дисперсной фазы n и дисперсионной среды n₀.

Напряженность электрического поля Е характеризует плотность энергетического потока подающего света (его интенсивность) и пропорциональна квадрату амплитуды волны, излучаемой электрическим диполем (частицей дисперсной фазы). А поскольку амплитуда волны пропорциональна квадрату частоты колебаний диполя, то интенсивность рассеянного света Ј_р пропорциональна частоте колебаний диполя в четвертой степени или обратно пропорциональна длине волны λ в четвертой степени.

Если падающий свет не поляризован, то интенсивность рассеянного света зависит от направления распространения излучения: Ј_р пропорциональна (1+cos 2 Θ), где Θ – угол между направлениями падающего и рассеянного света ( угол рассеяния).

Таким образом, интенсивность рассеянного света различна в разных направлениях, при этом рассеянный свет частично поляризован. Рассеяние и поляризацию света частицей во всех направлениях характеризует векторная диаграмма Ми (рис.1). Стрелка указывает направление падающего луча. Незаштрихованная область соответствует интенсивности неполяризованного света, заштрихованная – поляризованной части.

Как видно из диаграммы, рассеянный свет не поляризован в направлении падающего луча и под углом 180 о . Максимально поляризован свет, рассеянный под углом 90 о к падающему лучу.

Теория Рэлея применима к разбавленным коллоидным растворам, поэтому возможность вторичного рассеяния не учитывается, и интенсивность рассеянного света пропорциональна числу частиц в единице объема, ν.

Уравнение Рэлея для интенсивности света Ј_р , рассеянного единицей объема дисперсной системы со сферическими частицами, не проводящими электрический ток, радиусом, значительно меньшим длины волны падающего света (r ≤ 0,1λ), на расстоянии R от частиц, в направлении, составляющем угол Θ с направлением падающего луча, имеет вид:

J_р= (2)

F = (3)

J₀ – интенсивность падающего света;

ν — число частиц дисперсной фазы в единице объема (частичная концентрация);

и — соответственно, показатель преломления вещества дисперсной фазы и дисперсионной среды;

— объем одной частицы.

Рис.1. Диаграммы Ми, характеризующие рассеяние и поляризацию света сферическими частицами, не проводящими электрический ток:

а) малой; б) крупной частицей

Рассмотрим влияние различных параметров на интенсивность рассеянного света в соответствии с уравнением Рэлея.

1. Уравнение (2) применимо при отсутствии поглощения света, для «белых» неметаллических золей.

2. Область строгой применимости уравнения ограничена условием где r – радиус частиц дисперсной фазы. Для видимой части спектра это соответствует значениям радиуса r -6 см. Зависимость от r используется для определения размеров частиц дисперсных систем. Превышение указанных размеров частиц и приближение их к значениям приводит к снижению показателя степени при в уравнении Рэлея с 4 до 2,8. Нижняя граница показателя степени соответствует значениям r , когда явление рассеяния заменяется отражением света. Когда значение показателя степени при становится меньше 4, закон Рэлея перестает соблюдаться и для определения радиуса частиц пользуются эмпирическими методами. Наиболее распространен из них рассмотренный ниже метод Геллера.

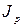
3. Зависимость интенсивности рассеянного света от концентрации частиц используется для определения концентрации (в отсутствие многократного рассеяния).

4. Согласно уравнению Рэлея, чем выше дисперсность частиц, тем меньше рассеяние. Приближение размеров частиц к молекулярным приводит к исчезновению опалесценции.

5. обратно пропорциональна λ 4 , т.е. при прохождении через коллоидный раствор пучка белого света рассеиваются в основном короткие волны, т.е. синяя область спектра. Это проявляется в голубоватой окраске коллоидных систем при боковом наблюдении. При рассмотрении кюветы с коллоидным раствором в проходящем свете, т.е. когда источник света по отношению к наблюдателю находится за кюветой, — раствор имеет оранжево – красные оттенки. Указанная закономерность объясняет применение синего цвета для светомаскировки и красного для сигнализации. Голубой цвет неба также объясняется опалесценцией, рассеиванием коротких волн солнечного излучения атмосферой Земли. При восходе и заходе солнца мы наблюдаем свет, прошедший через атмосферу, поэтому небо мы воспринимаем окрашенным в оранжево – красные тона.

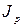
6. Разность показателей преломления частицы и среды весьма мала у растворов высокомолекулярных соединений и некоторых эмульсий. Светорассеяние для таких систем мало (в соответствии с уравнением (2)).

Видео:Шаталов за одну минуту доказывает теорему, на которую традиционно выделяется 45 минут урока!Скачать

2.4. Оптические свойства коллоидных систем
2.4.1. Рассеяние света в золях

Если коллоидные системы наблюдать в проходящем и боковом свете, то можно увидеть интересные явления: бесцветный золь в проходящем свете кажется прозрачным, а в боковом свете — мутным; луч света, проходя через золь, оставляет в нем светлую полосу. Это явление называется опалесценцией.

В 1869 г. Дж. Тиндаль установил, что если направить на золь пучок света, то внутри золя можно увидеть светящийся голубым светом конус. Стакан с золем должен быть затемнен, тогда конус виден особенно отчетливо. Схема опыта Тиндаля приведена на рис. 2.15.

При прохождении света через золь происходят следующие явления: поглощение (абсорбция) света, преломление света, отражение света, рассеяние света.

Явление опалесценции, конус Тиндаля — это следствие рассеяния света. Теорию этого явления разработал английский ученый Дж. У. Рэлей (1871 г.).

Если радиус частиц золя меньше длины полуволны падающего света (r 3 ); V – объем одной частицы; l – длина волны падающего света; n₂, n₁ – показатели преломления дисперсной фазы и дисперсионной среды.

Из уравнения Рэлея следует, что яркость опалесценции растет с уменьшением длины волны.

Голубое свечение обусловлено тем, что светорассеяние коротких волн (синих и фиолетовых) происходит интенсивнее, чем длинных (красных и желтых).

В проходящем свете относительное содержание лучей с короткой длиной волны будет уменьшаться, поэтому мутные среды, опалесцирующие голубым светом, в проходящем свете кажутся красноватыми или даже красными, если мутность достаточно сильна.

Интенсивность рассеянного света зависит от степени дисперсности. Наибольшее светорассеяние будет в коллоидных системах, меньше оно в грубодисперсных системах. В последних будет преобладать отражение, а не рассеяние света.

Для систем, содержащих частички металлов, проводящих электрический ток, все зависимости становятся гораздо сложнее. Яркость рассеянного света, на которую влияет длина волны, обычно проходит через максимум, характерный для данного типа частиц и определяется его индивидуальными оптическими постояннымими; кроме того, этот максимум является функцией степени дисперсности системы.

Рис. 2.16. Зависимость коэффициента объемного рассеяния света от размера частиц белого пигмента.

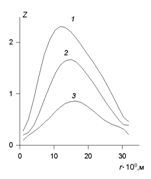
На рис. 2.16 приведен пример зависимости коэффициента рассеяния света от размера частиц. Видно, что зависимость интенсивности рассеянного света от дисперсности некоторых пигментов экстремальны и существует такой размер частиц r_m_ax, при котором рассеяние наибольшее. Интересно отметить, что, например, белый пигмент при r r_m_ax – желтоватый.

Следовательно, радиус частиц и их распределение по размерам определяют изменение оттенка или даже цвета пигмента в результате рассеяния различной части спектра. Поглощение света наряду с его рассеянием делает зависимость цвета дисперсии (в водной среде или в полимерной пленке) еще более сложной. Установлено, что максимум рассеяния света и размер частиц связаны уравнением

(2.2.104)

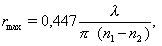
где l – длина волны падающего света; n₁, n₂ – коэффициенты преломления света дисперсионной средой и дисперсной фазой.

Используя это уравнение можно рассчитать необходимую степень дисперсности частиц пигмента, необходимую для максимального рассеяния света с заданной длиной волны l. Зависимость степени рассеяния света от размера частиц приводит к тому, что при диспергировании будет изменяться не только оттенок белого пигмента, но и кажущийся цвет окрашенного пигмента.

Уравнение Рэлея, также как и уравнение (2.2.104), справедливо только для систем с дисперсными частицами правильной сферической формы. Для систем с асимметричными частицами созданы теории, в которых рассеяние света связывают с углом его падения. Эти теории и соответствующие уравнения здесь мы не рассматриваем.