Уравнение рэлея и его анализ

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ

Гетерогенность дисперсных систем является причиной их оптической неоднородности и вызывает изменение направления световых, электронных, ионных и других лучей на межфазных поверхностях, а также неодинаковое поглощение или пропускание лучей веществами сопряженных фаз дисперсной системы. Всё это является причиной появления целого ряда специфических оптических явлений, присущих только коллоидным системам. Отличие оптических свойств коллоидных систем от свойств однородных сред привело к созданию целого ряда оптических методов исследования дисперсных систем, которые широко используются для изучения состава и структуры фаз, свойств межфазных поверхностей, дисперсности системы, а также природы, состава и структуры поверхностных слоёв.

Теоретические основы оптических явлений, характерных для дисперсных систем, и оптические методы их исследования следует изучить по учебникам, перечень которых приведен в списке литературы. В данном методическом пособии даётся только краткое теоретическое введение.

Основная часть издания посвящена практической части раздела «оптические свойства дисперсных систем» курса коллоидной химии и содержит подробное описание лабораторной работы по теме с практическими рекомендациями по её выполнению, обработке полученных данных и составлению отчета. Перед началом работы необходимо прочитать и принять к неукоснительному исполнению правила по технике безопасности, которые приведены в начале описания лабораторной работы и являются дополнением к общему инструктажу, проводимому со студентами в начале семестра.

Освоение практической части следует начинать только после изучения теории. Для теоретической подготовки по теме ниже приводится план теоретического коллоквиума. В конце методического пособия приведено приложение, которое является вспомогательным материалом, полезным для самоконтроля: контрольные вопросы и задачи.

ПЛАН ТЕОРЕТИЧЕСКОГО КОЛЛОКВИУМА

1. Общая характеристика оптических явлений.

2. Явление рассеяния света. Эффект Тиндаля. Влияние размеров частиц на вид индикатриссы рассеяния (диаграмма Ми).

3. Уравнение Рэлея и его анализ.

4. Светорассеяние токопроводящими сферическими частицами.

5. Абсорбция света. Уравнение Бугера – Ламберта — Бера. Оптическая плотность раствора, светопропускание, относительное поглощение.

6. Оптические методы исследования коллоидных систем: (принципиальные основы метода, его возможности и границы применимости):

а) световая и электронная микроскопия;

г) нефелометрия; определение молярной массы макромолекул.

7. Окраска коллоидных систем.

8. Лабораторная работа. Определение размеров частиц дисперсных систем турбидиметрическим методом:

a) Принципиальная оптическая схема фотоэлектроколориметра;

б) Определение размеров частиц дисперсных систем, подчиняющихся уравнению Рэлея;

в) Определение размеров частиц дисперсных систем, не подчиняющихся уравнению Рэлея, метод Геллера.

9. Самоподготовка по контрольным вопросам и задачам в приложении.

СПИСОК ЛИТЕРАТУРЫ

1. Фролов Ю.Г. Курс коллоидной химии. М., Химия, 1982г., с.245-267.

2. Боюцкий С.С. Курс коллоидной химии. М., Химия, 1975г., с. 33-53

3. Фридрихсберг Д.А. Курс коллоидной химии. Л., Химия, 1984г., с.38-44.

4. Лабораторные работы и задачи по коллоидной химии.- Под. ред. Ю.Г. Фролова и А.С. Гродского. М., Химия, 1986г., с.111-117.

5. Расчёты и задачи по коллоидной химии. Под ред. В.И.Барановой. М., Высш. шк., с. 254-260.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

РАССЕЯНИЕ СВЕТА, УРАВНЕНИЕ РЭЛЕЯ И ЕГО АНАЛИЗ

При падении луча света на дисперсную систему возможно его прохождение или преломление, а также отражение, рассеяние или поглощение света частицами дисперсной фазы. Прохождение света характерно для прозрачных гомогенных сред. Отражение – для микрогетерогенных и грубодисперсных систем с размерами частиц, превышающими длину волны падающего света (0,4 — 0,7 мкм), и проявляется в виде мутности суспензий, эмульсий и аэрозолей. Для коллоидных систем с радиусом частиц меньше длины волны падающего света характерны явления рассеяния света (опалесценция) и его поглощение (абсорбция).

Теория светорассеяния для сферических частиц, не проводящих электрический ток, разработана Рэлеем.

Дисперсные системы с размерами частиц, меньше длины световой волны, рассеивают свет во всех направлениях. При этом каждая точка неоднородности становится источником вторичных электромагнитных колебаний с частотой, равной частоте волны падающего света (дифракция). Частица представляет собой, таким образом, наведенный диполь, равный произведению поляризуемости частицы α на напряженность электрического поля Е:

Интенсивность рассеянного света определяется величинами, входящими в уравнение (1). Поляризуемость частицы α пропорциональна её объёму V, а интенсивность рассеяния света пропорциональна квадрату поляризуемости и, следовательно, квадрату объёма частицы. Таким образом, с ростом размера частиц интенсивность рассеяния возрастает. На поляризуемость влияет также разность показателей преломления дисперсной фазы n и дисперсионной среды n₀.

Напряженность электрического поля Е характеризует плотность энергетического потока подающего света (его интенсивность) и пропорциональна квадрату амплитуды волны, излучаемой электрическим диполем (частицей дисперсной фазы). А поскольку амплитуда волны пропорциональна квадрату частоты колебаний диполя, то интенсивность рассеянного света Ј_р пропорциональна частоте колебаний диполя в четвертой степени или обратно пропорциональна длине волны λ в четвертой степени.

Если падающий свет не поляризован, то интенсивность рассеянного света зависит от направления распространения излучения: Ј_р пропорциональна (1+cos 2 Θ), где Θ – угол между направлениями падающего и рассеянного света ( угол рассеяния).

Таким образом, интенсивность рассеянного света различна в разных направлениях, при этом рассеянный свет частично поляризован. Рассеяние и поляризацию света частицей во всех направлениях характеризует векторная диаграмма Ми (рис.1). Стрелка указывает направление падающего луча. Незаштрихованная область соответствует интенсивности неполяризованного света, заштрихованная – поляризованной части.

Как видно из диаграммы, рассеянный свет не поляризован в направлении падающего луча и под углом 180 о . Максимально поляризован свет, рассеянный под углом 90 о к падающему лучу.

Теория Рэлея применима к разбавленным коллоидным растворам, поэтому возможность вторичного рассеяния не учитывается, и интенсивность рассеянного света пропорциональна числу частиц в единице объема, ν.

Уравнение Рэлея для интенсивности света Ј_р , рассеянного единицей объема дисперсной системы со сферическими частицами, не проводящими электрический ток, радиусом, значительно меньшим длины волны падающего света (r ≤ 0,1λ), на расстоянии R от частиц, в направлении, составляющем угол Θ с направлением падающего луча, имеет вид:

J_р= (2)

F = (3)

J₀ – интенсивность падающего света;

ν — число частиц дисперсной фазы в единице объема (частичная концентрация);

и — соответственно, показатель преломления вещества дисперсной фазы и дисперсионной среды;

— объем одной частицы.

Рис.1. Диаграммы Ми, характеризующие рассеяние и поляризацию света сферическими частицами, не проводящими электрический ток:

а) малой; б) крупной частицей

Рассмотрим влияние различных параметров на интенсивность рассеянного света в соответствии с уравнением Рэлея.

1. Уравнение (2) применимо при отсутствии поглощения света, для «белых» неметаллических золей.

2. Область строгой применимости уравнения ограничена условием где r – радиус частиц дисперсной фазы. Для видимой части спектра это соответствует значениям радиуса r -6 см. Зависимость от r используется для определения размеров частиц дисперсных систем. Превышение указанных размеров частиц и приближение их к значениям приводит к снижению показателя степени при в уравнении Рэлея с 4 до 2,8. Нижняя граница показателя степени соответствует значениям r , когда явление рассеяния заменяется отражением света. Когда значение показателя степени при становится меньше 4, закон Рэлея перестает соблюдаться и для определения радиуса частиц пользуются эмпирическими методами. Наиболее распространен из них рассмотренный ниже метод Геллера.

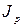
3. Зависимость интенсивности рассеянного света от концентрации частиц используется для определения концентрации (в отсутствие многократного рассеяния).

4. Согласно уравнению Рэлея, чем выше дисперсность частиц, тем меньше рассеяние. Приближение размеров частиц к молекулярным приводит к исчезновению опалесценции.

5. обратно пропорциональна λ 4 , т.е. при прохождении через коллоидный раствор пучка белого света рассеиваются в основном короткие волны, т.е. синяя область спектра. Это проявляется в голубоватой окраске коллоидных систем при боковом наблюдении. При рассмотрении кюветы с коллоидным раствором в проходящем свете, т.е. когда источник света по отношению к наблюдателю находится за кюветой, — раствор имеет оранжево – красные оттенки. Указанная закономерность объясняет применение синего цвета для светомаскировки и красного для сигнализации. Голубой цвет неба также объясняется опалесценцией, рассеиванием коротких волн солнечного излучения атмосферой Земли. При восходе и заходе солнца мы наблюдаем свет, прошедший через атмосферу, поэтому небо мы воспринимаем окрашенным в оранжево – красные тона.

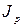
6. Разность показателей преломления частицы и среды весьма мала у растворов высокомолекулярных соединений и некоторых эмульсий. Светорассеяние для таких систем мало (в соответствии с уравнением (2)).

Видео:Вывод формулы Планка, Рэлея-Джинса, ультрафиолетовая катастрофа, подсчёт числа модСкачать

Оптические свойства коллоидных систем

Оптические свойства коллоидных систем определяются их гетерогенностью и дисперсностью. Изучение оптических свойств позволяет решить множество задач, например, можно определить наличие коллоидных частиц, их размер, форму, концентрацию.

5 видов взаимодействия световой волны с веществом:

1. Поглощение;
2. Преломление;
3. Рассеяние;
4. Отражение;
5. Пропускание

Но в зависимости от длины волны и размеров частиц преобладают определенные виды:

Если в системе нет никаких частиц с другим показателем преломления, то система будет считаться оптически пустой и рассеяния не будет. Если есть, то электрическое поле волны будет возбуждать электроны и начнется испускание света, при этом длина волны падающего света будет совпадать с рассеянным. В дисперсных системах источниками рассеяния света являются частицы дисперсной фазы.

Эффект Тиндаля — оптический эффект, рассеивание света при прохождении светового пучка через оптически неоднородную среду. Обычно наблюдается в виде светящегося конуса (конус Тиндаля), видимого на тёмном фоне.

Видео:2.5. Рассеяние Релея. Закройте, дует!Скачать

Теория светорассеяния Рэлея​

Настоящее имя Рэлея Джон Уильям Стретт, Лорд Рэлей. Рэлей открыл открыл аргон.

В общем случае уравнение Рэлея упрощается к виду

Видео:89. Формула Рэлея ДжинсаСкачать

Уравнение рэлея и его анализ

webkonspect.com — сайт, с элементами социальной сети, создан в помощь студентам в их непростой учебной жизни.

Здесь вы сможете создать свой конспект который поможет вам в учёбе.

Чем может быть полезен webkonspect.com:

• простота создания и редактирования конспекта (200 вопросов в 3 клика).
• просмотр конспекта без выхода в интернет.
• удобный текстовый редактор позволит Вам форматировать текст, рисовать таблицы, вставлять математические формулы и фотографии.
• конструирование одного конспекта совместно с другом, одногрупником.
• webkonspect.com — надёжное место для хранения небольших файлов.

💥 Видео

3 Теорема лорда РэлеяСкачать

Как выучить Химию с нуля за 10 минут? Принцип Ле-ШательеСкачать

Как расставлять коэффициенты в уравнении реакции? Химия с нуля 7-8 класс | TutorOnlineСкачать

Химические уравнения // Как Составлять Уравнения Реакций // Химия 9 классСкачать

Теория вероятностей #13: виды ПРВ: гауссовая, равномерная, рэлея, экспоненциальнаяСкачать

Составление уравнений химических реакций. 1 часть. 8 класс.Скачать

Структурный анализ вещества. Вульф и Брегг. X-Ray. Химия – простоСкачать

РЕАКЦИИ ИОННОГО ОБМЕНА, ИОННОЕ УРАВНЕНИЕ - Урок Химия 9 класс / Подготовка к ЕГЭ по ХимииСкачать

Расстановка Коэффициентов в Химических Реакциях // Подготовка к ЕГЭ по ХимииСкачать

Шаталов за одну минуту доказывает теорему, на которую традиционно выделяется 45 минут урока!Скачать

Нормальное Распределение за 6 МинутСкачать

Формула Релея-ДжинсаСкачать

Урок 434. Фотоэффект. Законы фотоэффектаСкачать

Закон БернуллиСкачать

Теорема Куранта-Фишера. Отношения Рэлея. Операторные уравнения. Матрица по Муру-Пенроузу. 19 лекцияСкачать

Тепловое излучение и закон смещения ВинаСкачать

Продукция для прохождения курса "Раскрой скрытый потенциал своей иммунной системы" / Дадали В.А.Скачать