Уравнение регрессии в statistica 10

Видео:Множественная регрессия в программе Statistica (Multiple regression)Скачать

ГЛАВА 16 Примеры анализа данных в системе STATISTICA

В этой главе мы рассмотрим несколько примеров анализа данных с помощью системы STATISTICA. Первый пример относится к области маркетинга (мы показываем возможности модуля Множественная регрессия), три следующие примера к промышленным приложениям (мы показываем возможности модулей Планирование эксперимента и Карты контроля качества), пятый пример иллюстрирует возможности STATISTICA по наложению результатов анализа на географические карты.

Еще раз отметим, что современная STATISTICA — это средство разработки приложений в конкретных областях (бизнесе, медицине, промышленности и др.). Библиотека STATISTICA содержит более 10 000 тщательно отлаженных и проверенных на практике процедур анализа данных. Развитие системы естественно приводит к созданию средств разработки собственного интерфейса и использования библиотеки STATISTICA для создания оригинальных модулей, включающих, наряду с процедурами STATISTICA, алгоритмы разработчика. Все эти процедуры объединяются общим интерфейсом, средствами управления данными и графикой STATISTICA.

Именно в создании средств для разработки приложений мы видим будущее систем анализа данных.

Пример основан на реальных данных, описывающих рынок пива в Греции (см. статью Kioulofas К. Е. «An Application of Multiple Regression Analysis to the Greek Beer Market» в журнале «Journal of Operational Research Society», Vol. 36, № 8, p. 689-696,1985).

Известно, что этот рынок поделен между 5 фирмами, обозначенными далее А, В, С, D и Е. До 1981 года на рынке присутствовали фирмы А, В и С, в 1981 году на рынок пришли фирмы D и Е. Но уже в’ 1983 году фирма D не выдержала конкуренции, а у фирмы А возникли финансовые проблемы.

В следующей таблице представлены объемы продаж в отрасли и доля каждой фирмы.

Можно заметить, что после появления фирм D и Е произошло резкое снижение доли фирмы А. Две новые фирмы D и Е по-разному освоили рынок. Фирма D имела большие производительные способности, чем фирма Е, но заметно отстала по объемам продаж. Этот пример интересен тем, что показывает соотношение затрат на рекламу и производство.

Будем считать, что основным показателем эффективности рекламы является объем продаж фирмы. В этой таблице представлены расходы на рекламу каждой фирмы и ее доля в рекламе.

Понятно, что вхождение в отрасль фирм D и Е потребовало больше расходов на рекламу (в процентном отношении к объему продаж). Это отчетливо видно из следующей таблицы:

Заметим, фирма D в 1982 году резко снизила расходы на рекламу, что, возможно, стало причиной потери рынка.

Предполагается, что для рекламы используются следующие средства массовой информации: телевидение, газеты, журналы и радио.

Эффективность рекламы в каждом случае различна, и возникает вопрос о количественных зависимостях между объемом продаж и расходами на рекламу в каждом из средств массовой информации. Обычно доля телевидения составляет 70-90%, и поэтому в таблице, представляющей распределение расходов на рекламу между средствами массовой информации, все СМИ, кроме телевидения, объединены в одну группу «другие».

На реальный объем продаж пива влияют также такие факторы, как температура воздуха, число туристов и индекс потребительских цен (инфляция).

В предлагаемой модели теоретическая зависимость основывается на предположении, что объем продаж за период t (далее это месяцы) является функцией объема продаж за прошлый период расходов на рекламу в периоды t и t-1, количества туристов, значений температуры и индекса розничных цен.

S_t — объем продаж (в драхмах);

A_t — ассигнования на рекламу;

T_t — число туристов в месяц t;

W_t — средняя температура воздуха;

P_t — индекс розничных цен.

Итак, мы построили модель зависимости, но коэффициенты этой модели неизвестны. Эти коэффициенты оцениваются из исходных данных в модуле Множественная регрессия.

Оценка коэффициентов по методу наименьших квадратов выявила статистическую незначимость переменных W_t и P_t, и они были исключены из дальнейшего анализа.

В результате получилось уравнение, содержащее меньшее число переменных:

Оценим коэффициенты этого уравнения, используя реальные данные. Для анализа использовались данные о месячных продажах за 2 года. Число наблюдений равнялось 24. Результаты регрессии приведены в таблице:

Значения коэффициента детерминации R 2 , близкие к единице, говорят о хорошем приближении линии регрессии к наблюдаемым данным и о возможности построения качественного прогноза.

Низкое значение коэффициента детерминации R 2 для фирмы D объясняется низкой эффективностью рекламной кампании и трудностями на административном уровне. Можно сделать вывод, что модель плохо применима к фирме D.

Статистики Дарбина—Уотсона свидетельствуют об отсутствии автокорреляции остатков при 5%-м уровне значимости, т. к. все ее значения по модулю меньше 1,96.

Все значения регрессионных коэффициентов значимы при уровне значимости 0,5, за исключением коэффициентов при A_t для фирм В, D и Е.

Одним из возможных объяснений этого факта является то, что показатели этих фирм зависят от рекламной деятельности за прошлый период времени, то есть от А_t-1

Это подтверждается тем, что для этих фирм коэффициенты при A_t-1 значимы на уровне 95%. Более того, можно заметить, что показатели всех фирм, кроме фирмы Е, имеют положительную корреляцию с числом туристов. Незначительную корреляцию между туризмом и объемами продаж фирмы Е можно объяснить недавним появлением этой фирмы. Объемы продаж всех фирм также находятся под влиянием объемов продаж в прошлом периоде, S_t-1 возможно, благодаря эффекту «привычки» потребителей к торговым маркам. Значимость этого параметра с распределенным лагом также наводит на мысль о некоторых обучающих эффектах.

Продажи фирмы А имеют значительную положительную корреляцию с ее расходами на рекламу за период t, что отличает ее от других фирм. Окончательно взаимосвязь между рыночными продажами и совокупными расходами на рекламу положительна и значима при уровне 5%.

Представленные выше результаты регрессии образуют основу оценки эффективности совокупных расходов на рекламу.

Покажем, как строятся такие модели в системе STATISTICA. Для этих целей обычно используется модуль Множественная регрессия.

В этом модуле собраны методы, позволяющие оценить зависимость одной переменной от нескольких других переменных.

Переменная, для которой строится зависимость, называется зависимой (по-английски dependent variable). Эта переменная входит в левую часть уравнения, описывающего зависимость (см. уравнение (*)). Переменные, от которых мы хотим построить зависимость, называются независимыми переменными (по-английски independent variables) или предикторами (от английского predict — предсказывать). Эта переменная входит в правую часть уравнения, описывающего зависимость. Сам термин множественная регрессия (по-английски multiple regression) означает, что модель может содержать несколько предикторов, позволяющих предсказывать зависимую переменную.

Итак, общая идея состоит в том, чтобы по значениям предикторов предсказывать значения зависимой переменной, например, по значениям продаж и расходам на рекламу в текущем и предыдущем месяце предсказывать продажи в следующем месяце.

Конечно, количество предикторов можно увеличить, например, ввести объем продаж у конкурентов или какие-то другие, имеющие смысл и доступные наблюдению переменные. Однако здесь имеется тонкость, предикторы могут оказаться зависимыми между собой.

Переменные, которые следует включить в модель, определяет специалист в предметной области. Затем нужно выполнить следующие действия.

Шаг 1. Запустите модуль Множественная регрессия.

Шаг 2. Введите исходные данные в файл системы STATISTICA. Назовите его, например, Beer.sta.

Шаг 3. Определите переменные в модели. Задайте S в качестве зависимой переменной и S1. P — в качестве независимых переменных, или предикторов. После этого стартовая панель модуля будет выглядеть так:

Шаг 4. Нажмите кнопку ОК. Появится диалоговое окно результатов, в котором отображаются итоги стандартной процедуры.

Измените процедуру на Пошаговую с включением. Для этого нажмите на кнопку Отмена и в появившемся диалоговом окне Определение модели выберите в поле Процедура опцию Пошаговая с включением. В этой процедуре система начинает построение модели с одного предиктора, затем, используя F-критерий, в модель включается еще один предиктор и т. д. На каждом шаге вычисляется коэффициент множественной корреляции. Квадрат коэффициента множественной корреляции, коэффициент детерминации, свидетельствует о качестве построенной модели. Нажмите кнопку ОК.

В появившемся окнеПошаговая множественная регрессия снова нажмите ОК.

Теперь перед вами диалоговое окно результатов, полученных с помощью пошаговой процедуры с включением. Следует отметить, что в нем указаны стандартизованные коэффициенты регрессии.

Заметим, если вы предполагаете, что в модели должно присутствовать небольшое число предикторов, то естественно использовать пошаговый метод с включением предикторов. Если вы предполагаете, что в модели должно присутствовать большое число предикторов, то естественно использовать метод с исключением.

Шаг 5. Нажмите кнопку Итоговая таблица регрессии. Появится таблица результатов с подробными статистиками.

В столбце БЕТА показаны стандартизованные коэффициенты регрессии, а в столбце В — нестандартизованные коэффициенты. Все коэффициенты в таблице значимы, так как р-значения для каждого из них меньше заданной величины 0»05.

Шаг 6. В окне результатов нажмите кнопку Анализ остатков.

Шаг 7. В диалоговом окне Анализ остатков нажмите кнопку Статистика Дарбина—Уотсона. Эта статистика позволяет исследовать зависимость между остатками. Формально остатки представляют собой разность: наблюдаемые значения зависимой переменной минус оцененные с помощью модели значения зависимой переменной.

Зачем проверять зависимость остатков? Идея проста: если остатки существенно коррелированны (зависимы), то модель неадекватна (нарушено важное предположение о независимости ошибок в регрессионной модели).

Рассмотрим более подробно статистику Дарбина—Уотсона. Мы уделяем этой статистике так много внимания, потому что статистика Дарбина—Уотсона является стандартом для проверки некоторых видов зависимости остатков и с ней нужно научиться работать.

Статистика Дарбина—Уотсона используется для проверки гипотезы о том, что остатки построенной регрессионной модели некоррелированы (корреляции равны нулю), против альтернативы: остатки связаны авторегрессионной зависимостью вида:

где d_i независимые случайные величины, имеющие нормальное распределение с параметрами (0, s), i = 1 . n».

Формально статистика Дарбина—Уотсона вычисляется следующим образом:

Иными словами, сумма квадратов первых разностей остатков нормируется суммой квадратов остатков. Проведя вычисления, вы легко выразите статистику Дарбина—Уотсона через коэффициент корреляции: d = 2(1 — р).

Критические точки статистики Дарбина—Уотсона табулированы (см. например, Драйпер Н., Смит Г. Прикладной регрессионный анализ. М.: Финансы и статистика, т. 1. с. 211, см. также таблицу, показанную ниже).

В таблице приведены два критических значения статистики Дарбина—Уотсо-на: DL_k и DU_k — нижнее и верхнее, зависящие как от числа наблюдений, по которым оцениваются параметры, так и от числа предикторов k, которые включены в модель.

На графике видно, как меняются значения DL_k и DU_k в зависимости от числа наблюдений (k = 1, 2, 3, 4, 5).

Число наблюдений, для которого рассчитаны критические значения, указано в заголовках строк приведенной таблицы.

Итак, вы находите строку с нужным числом наблюдений и два смежных столбца с нужным числом предикторов. На пересечении строки и столбцов располагаются нижние и верхние критические точки статистики Дарбина—Уотсона.

Если нужно проверить гипотезу: «остатки независимы, то есть р =0», против общей альтернативы р не равно 0, поступают следующим образом. Вычисляют значение статистики Дарбина—Уотсона d. Для данного числа наблюдений и числа предикторов находят критические точки DL_k и DU_k в таблице, составленной для определенного уровня а. В приведенной таблице уровень a=0,05

Если d DU_k и 4 — d > DU_k, то гипотеза о независимости остатков не отвергается на уровне 2a.

Если нужно проверить гипотезу: «остатки независимы р = 0», против альтернативы р > 0, то есть остатки положительно автокоррелированы, поступают следующим образом. Вычисляют значение статистики Дарбина—Уотсона d. Находят по таблице критические точки DL_k и DU_k, вычисленные для определенного уровня a. Заметьте, в приведенной таблице a=0,05.

Если d DU_k, то гипотеза о независимости не отвергается на уровне a.

После того как мы познакомились со статистикой Дарбина—Уотсона, продолжим работу в модуле Множественная регрессия.

Шаг 8. Нажмите кнопку Предсказанные и наблюдаемые.

Шаг 9. Вернитесь в окно Результаты множественной регрессии и нажмите кнопку Предсказать зависимую переменную. Далее в полях А1 и S1 укажите значения текущего месяца, а в полях Т и А — значения на следующий месяц.

Нажмите кнопку ОК. Появится таблица результатов предсказания. На рисунке выделена ячейка, содержащая прогнозируемый объем продаж на следующий месяц.

Этот пример относится к промышленной статистике (см. Cornell J. А. (1990). How to Apply Response Surface Methodology, vol. 8 in Basic References in Quality Control: Statistical Techniques, edited by S. S. Shapiro and E. Mykytka. Milwaukee: American Society for Quality Control).

Любая машина или станок, используемые на производстве, позволяют операторам производить настройки, чтобы воздействовать на качество производимого продукта. Изменяя настройки, инженер стремится добиться максимального эффекта, а также выяснить, какие факторы играют наиболее важную роль в улучшении качества продукции.

В системе STATISTICA имеется мощный модуль планирования экспериментов, позволяющий эффективно планировать и анализировать эксперименты.

Задача состояла в том, чтобы исследовать факторы, влияющие на качество производимых пластиковых дисков.

Известно, что наибольшее влияние на качество оказывают следующие два фактора:

1) материал, характеризующийся отношением наполнителя к эпоксидной резине,

2) расположение диска в форме.

В качестве зависимой переменной рассматривалась плотность полученного диска.

Сначала использовался дробный факторный план 2 2 для того, чтобы определить адекватность модели первого порядка. В этой модели оба фактора комбинировались друг с другом на верхних и нижних значениях (всего имеется 4 комбинации). Но оказалось, что модель оказалась адекватной лишь для некоторой области значений факторов и неадекватной для всей значений факторов. На самом деле зависимость между факторами и откликом была нелинейной. Поэтому было решено использовать центральный композиционный план и применить модель второго порядка.

Центральный композиционный план может состоять из куба и звезды. Куб соответствует полному факторному плану — точки эксперимента располагаются в вершинах куба (фактически это факторный план 22).

Звезда содержит дополнительное множество точек, расположенных на одинаковых расстояниях от центра куба на отрезках, исходящих из центра и проходящих через каждую сторону куба.

В данном исследовании применялся ротатабельный план, в котором дисперсия отклика является постоянной во всех точках, одинаково удаленных от центра плана.

Пусть фактор А — это характеристика материала, из которого изготовлен диск, более точно, так называемое композиционное отношение (disk composition ratio), фактор В — положение диска в форме (position of disk in mold). Зависимая переменная, или отклик эксперимента, — плотность диска (Thickness).

Запустите модуль Планирование эксперимента.

На стартовой панели выберите Центральные композиционные планы, поверхности отклика и нажмите кнопку ОК.

В появившемся диалоговом окне выберите опцию Построение плана, а в поле Факторы/блоки/опыты — строку 2/1/10. Нажмите кнопку ОК.

Появится диалоговое окно План эксперимента для поверхности отклика. Нажмите на кнопку Имена факторов, значения и заполните таблицу в диалоговом окнеИтоги для переменных .

Нажмите кнопку Далее и выберите опции для настройки .отображения плана так, как показано на следующем рисунке. Сделайте точно все показанные настройки, чтобы получить нужный результат!

Просмотрите план. Для этого нажмите Просмотр/Правка/Сохранение.

Задание имени и сохранение экспериментального плана

Выберите Сохранить как файл данных. ; появится соответствующее диалоговое окно. Задайте имя плана disk.sta и нажмите кнопку ОК.

Вернитесь в диалоговое окно План эксперимента для поверхности отклика.

Нажмите кнопку Печать итогов. В зависимости от настроек вывода в диалоговом окне Параметры страницы/вывода результаты плана будут распечатаны на принтере или выведены в отчет.

В построенной таблице показан порядок сбора экспериментальных данных.

Данные, полученные в результате эксперимента, занесены в таблицу.

Видео:РЕГРЕССИОННЫЙ АНАЛИЗ STATISTICA #12Скачать

Лабораторная работа 5
Простая и множественная регрессии

Цель работы: обучить студентов строить модели прогноза на основе простой и множественной регрессий.

Оглавление

Видео:Множественная линейная регрессия в StatisticaСкачать

Пакет Statistica, 6.0

1. Простая регрессия

1. Открыть файл данных Poverty.sta через File – Open (Файл – Открыть). Приведенные данные основаны на сравнении результатов переписи 1960 и 1970 гг. для случайной выборки из 30 стран. Названия стран были введены как названия строк. Через пункт меню Data и выбора опции All Variable Specs укажем названия всех переменных этого файла:

POP_CHNG – Изменение населения за 1960-1970 гг.

N_EMPLD – Количество людей, занятых в сельском хозяйстве

PT_POOR – Процент семей, живущих ниже уровня бедности.

TAX_RATE – Ставка налога.

PT_PHONE – Процент квартир с телефоном.

PT_RURAL – Процент сельского населения.

AGE – Средний возраст.

Часть данных приведена в табл.1.

Таблица 1. Исходные данные

Теперь оценим связь параметра Pt_Poor, т. е. переменной, которая лучше всего отражает уровень бедности в стране, с другими параметрами. Таким образом, признак Pt_Poor считается независимой переменной, а все остальные параметры – зависимые. В данной задаче необходимо определить связь признака Pt_Poor с одним из других признаков.

1. Из меню Statistics – Advanced Linear/Nonlinear Models (Статистики-Расширенные линейные-нелинейные модели) выбрать General Linear Models (Общие линейные модели) для отображения стартовой панели (рис. 1).

Рис. 1. Стартовая панель общих линейных моделей

Выбрать в качестве типа анализа Simple regression (Простая регрессия) и в качестве метода решения – Quick specs dialog (Быстрый диалог). Затем нажать ОК для входа в диалоговое окно простой регрессии (рис. 2).

При нажатии клавиши Variables в этом окне появляется окно выбора переменных (рис. 3), в котором в качестве зависимой переменной следует указать признак Pt_Poor, а в качестве независимой – Pop_Chng.

Рис. 2. Диалоговое окно простой регрессии

Далее – нажать ОК для возврата к диалоговому окну регрессии.

Рис. 3. Окно выбора переменных

1. Нажав ОК в последнем окне, приходим к окну результатов регрессионного анализа (рис. 4), где при выделенной опции Summary (Итог) нужно нажать клавишу Coefficients для отображения рассчитанных коэффициентов регрессии между выделенными переменными.

Рис. 4. Итоговое окно регрессионного анализа

1. Коэффициенты регрессии представлены в табл. 2.

Таблица 2. Регрессионные коэффициенты

Полученное уравнение регрессии между переменными Pt_Poor и Pop_Chng имеет вид:

Pt_Poor = 26,2 — 0,4 Pop_Chng

Из уравнения следует, что на каждую единицу уменьшения населения приходится приблизительно 0,4 единицы увеличения числа семей, живущих ниже черты бедности. В таблице также приведены доверительные интервалы для обоих членов уравнения регрессии и стандартизированное значение коэффициента регрессии между выделенными переменными, равное -0,65. Эта величина также определяет и коэффициент корреляции между рассматриваемыми признаками.

2. Множественная регрессия

1. Открыть тот же файл данных Poverty.sta через File – Open (Файл – Открыть).
2. Из меню Statistics – Advanced Linear / Nonlinear Models (Статистики-Расширенные линейные-нелинейные модели) выбрать General Linear Models (Общие линейные модели) для отображения стартовой панели, как и в случае простой регрессии.

Выбрать в качестве типа анализа Multiple regression (Множественная регрессия) и в качестве метода решения – Quick specs dialog (Быстрый диалог). Затем нажать ОК для входа в диалоговое окно множественной регрессии (рис. 5).

Рис. 5. Диалоговое окно множественной регрессии

При нажатии клавиши Variables в этом окне появляется окно выбора переменных (рис. 6), в котором в качестве зависимой переменной следует указать признак Pt_Poor, а в качестве независимых – все остальные.

Рис. 6. Окно выбора переменных для множественной регрессии

(Отметим, что при определении переменных правого столбца вначале нужно выделить все переменные, а затем при нажатой клавише Ctrl отметить признак Pt_Poor). Далее – нажать ОК для возврата к диалоговому окну регрессии.

1. Нажав ОК в последнем окне, приходим к окну результатов регрессионного анализа, где при выделенной опции Summary (Итог) нужно нажать клавишу Coefficients для отображения рассчитанных коэффициентов регрессии между выделенными переменными. Полученные результаты приведены в табл. 3.

Таблица 3. Регрессионные коэффициенты

Эта таблица показывает регрессионные коэффициенты (В) и стандартизованные регрессионные коэффициенты (Beta). С помощью коэффициентов В устанавливается вид уравнения регрессии, которое в данном случае имеет вид

Включение в правую часть только этих переменных обусловлено тем, что лишь эти признаки имеют значение вероятности р меньше, чем 0,05 (см. четвертый столбец табл. 3). Такое значение вероятности принято при вычислении доверительных интервалов на коэффициенты регрессии

Величина коэффициентов Beta позволяет сравнить относительный вклад каждой независимой переменной в предсказание зависимой переменной. Как видно из таблицы, переменные Pop_Chng, Pt_Rural, (Изменение населения за 1960-1970 гг., процент сельского населения) являются наиболее важными предикторами: обладают статистической значимостью (выделены красным цветом). Регрессионный коэффициент для Pop_Chng отрицательный, что означает: чем меньше увеличение населения, тем больше число семей, живущих ниже черты бедности в соответствующей стране. Тот же коэффициент для переменной Pt_Rural – положительный: чем больше процент сельского населения, тем выше уровень бедности.

1. Для анализа остатков следует в окне диалога GLM Results нажать кнопку More results, после чего выделить закладку Residuals 1 для рассмотрения различных видов представления остатков. Обычно оцениваются стандартизированные остатки с целью выявления выбросов, превышающих ± 3 sigma. Для этого необходимо выбрать опцию Standardized в поле Resids for default plots и нажать кнопку Case no. & res для построения графика, аналогичного показанному на рис. 7.

В этом диалоге имеется много возможностей построения различных графиков. Большинство из них интерпретируются достаточно просто, в частности, гистограмма распределения остатков, однако графики нормального распределения требуют отдельных комментариев. Как известно, множественная линейная регрессия допускает линейные соотношения между переменными уравнения и нормальность остатков. Если эти допущения нарушены, то окончательное заключение может быть неверным. График нормального распределения представляет собой индикатор того, являются или нет отклонения от допущений значительными. Для построения графика нажать кнопку Normal в поле Probab. plots of resides.

Рис. 7. График остатков

Если наблюдаемые остатки нормально распределены, то все значения должны укладываться на прямой линии (или близко от нее) приведенного графика (рис. 8). В противном случае точки, изображающие остатки, будут отклоняться от прямой линии.

Рис. 8. Индикатор нормальности остатков

Видео:Линейный дискриминантный анализ в Statistica 10Скачать

Пакет Statgraphics 5.1

1. Простая регрессия

1. Открыть через меню File – Open – Open Data File файл данных Carsales (Продажа машин). Данные представляют собой количество продаваемых машин (в тыс. шт.) по месяцам на протяжении 6 лет. В табл. 4 приведена часть этих данных.

Таблица 4. Исходные данные

1. Через меню Relate – Simple Regression (Общность – Простая регрессия) перейти к окну простой регрессии. Выбрать в качестве независимой переменной параметр sales (продажи), независимой – переменную ADJUSTED (отрегулированные) и указать в поле Select: first(20) для ограничения объема данных первыми двадцатью строками. Результат – на рис. 9.

Рис. 9. Окно простой регрессии

Затем нажать ОК. На экране монитора появится окно результатов регрессионного анализа.

1. Среди табличных опций выделить следующие: Analysis Summary, Comparison of Alternative Models (Суммарный итог, сравнение альтернативных моделей). В первой таблице приводятся результаты расчета коэффициентов регрессионного уравнения, стандартные отклонения каждого коэффициента, значения статистик (табл. 5).

Таблица 5. Результат регрессионного анализа

Консультант дает следующее пояснение:

Выход показывает результаты подгонки модели простой линейной регрессии для описания связи между переменными sales и Adjusted. Уравнение подогнанной модели имеет вид:

sales = -289,341 + 1,04594*ADJUSTED.

Вследствие того, что Р-значение в таблице итогового анализа меньше, чем 0,01, то имеется статистически значимая связь между переменными при доверительном уровне 99 %.

R-Squared статистика определяет, что подогнанная модель объясняет 93,16 % всей вариации переменной sales.

В таблице сравнения альтернативных моделей (табл. 6) приводятся различные виды моделей и значения коэффициента R-Squared (коэффициента детерминации) для этих моделей. Чем больше величина этого коэффициента, тем лучше выбранная модель объясняет вариации в переменной sales.

Таблица 6. Сравнение различных моделей

Из табл. 6 видно, что лучшей моделью для подгонки этих данных является мультипликативная модель.

Для просмотра результатов подгонки данных различными моделями необходимо нажать правую клавишу мыши и в появившемся окне указать: Analysis Options (Анализ опций). В результате всплывает окно опций простой регрессии с различными типами моделей, показанное на рис. 10.

Рис. 10. Окно опций простой регрессии

1. Среди графических опций выделить Plot of Fitted Model (График подогнанной модели) и Residuals versus Row Number (Остатки в зависимости от номера строки). Эти графики показаны на рис. 11 и 12, соответственно.

Рис. 11. График подогнанной модели

Рис. 12. График остатков

Приведенные графики (для линейной модели) показывают, что выбранная модель не противоречит данным: значение коэффициента R-Squared (коэффициента детерминации) здесь составляет 93,16 %, а остатки имеют разные знаки отклонений от исходных данных, что, в свою очередь, не противоречит гипотезе о нормальном законе распределения остатков.

2. Множественная регрессия

1. Открыть тот же файл данных Carsales (Продажа машин).
2. Через меню Relate – Multiple Regression (Общность – Множественная регрессия) перейти к окну множественной регрессии. Выбрать в качестве независимой переменной параметр sales (продажи), независимых – все остальные переменные и указать в поле Select: first(20) для ограничения объема данных первыми двадцатью строками. Результат – на рис. 13.
3. По умолчанию из табличных опций открывается Analysis Summary (Итоговый анализ), которой достаточно для анализа результатов. Здесь приводятся результаты расчета коэффициентов регрессионного уравнения, стандартные отклонения каждого коэффициента, значения статистик (табл. 7).

Рис. 13. Окно множественной регрессии

Таблица 7. Результат регрессионного анализа

Консультант дает следующее пояснение:

Выход показывает результаты подгонки модели множественной линейной регрессии для описания связи между переменной sales и остальными независимыми переменными. Уравнение подогнанной модели имеет вид:

sales = -8655,36 + 1,01188* ADJUSTED + 0,411272* RESIDS + 92,7932* SIND -0,0565496* AVGS

R-Squared статистика, приведенная в Итоговом анализе, определяет, что подогнанная модель объясняет 98,5 % всей вариации переменной sales.

При оценке возможности упрощения модели заметим, что наибольшие значения величины Р, равные 0,972 и 0,355, принадлежат переменным RESIDS и AVGS. Так как значение Р больше или равно 0,10, то эти переменные не является статистически значимыми на 90-процентном или более высоком доверительном уровне, следовательно, можно рассмотреть возможность исключения этих признаков из дальнейшего анализа.

1. Среди графических опций выделить Component Effects и Residuals versus X. Проанализировать эти графики, изменяя переменные на горизонтальной оси.

Видео:РЕГРЕССИОННЫЙ АНАЛИЗ общая идея | АНАЛИЗ ДАННЫХ #16Скачать

Задание

По пакету Statistica, 6.0

1. Открыть файл Cars . sta, состоящий из 22 строк (марок автомашин) и 5 столбцов (признаков, характеризующих в нормированном виде эксплуатационные свойства машин: цена, ускорение, время остановки со скорости 80 миль в час, коэффициент сцепления с покрытием, расход топлива).

• уравнение линейной регрессии между ценой и расходом топлива (переменные price и mileage);
• уравнение множественной регрессии между ценой и всеми остальными признаками.

1. Смоделировать матрицу данных из 20 объектов и 3 признаков (см. работу №2) со средними значениями и СКО признаков, соответственно, (1;3), (5;10), (10; 25).

Видео:Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать

Примерф решения эконометрических задач в Statistica

Ниже приведено условия задач и текстовая часть решения. Закачка полного решения, в архиве rar, начнется автоматически через 10 секунд.

Видео:Регрессионный анализ (линейная регрессия) в StatisticaСкачать

Задача 1. Построение и анализ линейной множественной регре с сии

В таблице 1.1. приведены ежегодные данные о совокупных личных расходах ; располагаемых личных доходах ; расходах на табак для США на период с 1959 по 1983 годы. Оцените множественную регрессию между регрессандом (эндогенной пер е менной) Var 1 и регрессорами (экзогенными пер е менными) Var 2, Var 3 и Var 4 используя данные за 25 лет. Дайте интерпретацию коэффициентам ре г рессии. Исследуйте степень корреляционной зависимости между переменными. Проверьте остатки на н а личие автокорреляции и гетероскедастичность.

Ежегодные данные о потребительских расходах и

располагаемых личных д о ходах для США на период с 1959 по 1983 годы

Используем пакет Statistica 6.0, модуль Множественная регрессия .

Создадим новый документ с данными, введем число переменных – 4 и число регис т ров – 25. Введем наименования переменных и исходные данные.

Вызовем модуль Множественная регрессия . (Команда Статист и ка  Множественная регрессия). Выберем переменные (кнопка ( Variables ). Зависимая ( Dependent ) – Var 1 ; независ и мые ( Independent ) – Var 2 , Var 3 , Var 4 .

Нажмем кнопку ОК в правом углу стартовой панели.

Появится окно результатов множественной регрессии.

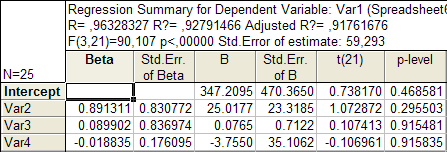
Результаты множественной регрессии в численном виде представлены в табл. 1.2.

В первом столбце таблицы 1.2 . даны значения коэффициентов beta — стандартизованные коэффициенты регрессионно го урав нения , во втором — стандартные ошибки beta , в третьем – В – точечные оценки пар а метров модели.

Далее, стандартные ошибки для коэффициентов модели В, значения ст а тис тик t-критерия и т.д.

Из таблицы 1.2 . мы видим, что оцененная модель имеет вид:

Var 1 = 347,2 + 25,018∙ Var 2 – 0,0765∙ Var 3 – 3 ,755 ∙ Var 4 (1.1)

TPE = 347,2 + 25,018 ∙ TIME – 0,0 765 ∙ PI – 3,755 ∙ TOB (1.2)

( t ) ( 0,738 ) (1, 073 ) ( 0,1074) (-0,107 )

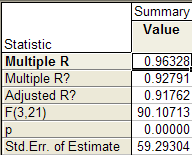
В верхней части таблицы 1.2 . и в таблице 1.3 . (а также в информационном окне) прив е дены следующие данные:

Коэффициент множественно й корреляции Multiple R = 0, 9633 ;

Коэффициент детерминации R-square = 0, 9279 ;

Скорректированный на поте ­ рю степеней свободы коэффициент множественной д е термина ции Adjusted R 2 = 0, 9 176 ;

Критерий Фишера F = 90,107 ;

Уровень значимости модели р

Стандартная ошибка оценки Std. Error of estimate = 59,293 .

Проанализируем данные множественной регрессии.

Табличное значение критерия Стьюдента, соответствующее доверител ь ной вероятности  = 0,95 и числу степеней свободы v = n – m – 1 = 21 ; t кр. = t 0,025;21 = 2,080.

Сравнивая расчетную t -статистику коэффициентов уравнения с табличным значением, заключаем, что все полученные коэффициенты стат и стически не значимы.

Уравнение (1.2 . ) выражает зависимость совокупных личных расходов ( TPE ) от времени ( TIME ), личного дохода ( PI ) и расходов на табак ( TOB ). Коэффициенты уравнения пок а зывают количественное воздействие каждого фактора на результативный показатель при неизменности других. В нашем случае совокупные личные расходы увеличиваются на 25,017 ден. ед. при увеличении времени на 1 ед. при неизменности показателей личного дохода и расходов на табак ; совокупные личные расходы увеличиваются на 0,0765 ден. ед. при увеличении показателя личного дохода на 1 ед. и неизменности показателей времени и расходов на табак ; совокупные личные расходы уменьшаются 3,755 ден. ед. при увеличении ра с ходов на табак на 1 ед. и неизменности показателей времени и личного дох о да.

Множественный коэффициент корреляции построенной модели (Multiple R) R = 0,9633 очень близок к единице, что говорит о высокой степени связи между исследуемыми факт о рами.

Коэффициент детерминации (R Square) R 2 = 0,9279, что говорит о том, что 92,79 % вари а ции переменной TPE объясняется вариацией переменных TIME , PI , TOB и только 7, 21 % приходятся на долю других неучтенных факторов.

Критическое (табличное) значение критерия Фишера для доверительной вероятн о сти  = 0,95 и числа степеней свободы v 1 = 25 – 3 = 22 и v 2 = 25 – 1 = 24: F кр . = F 0,05;22;24 = 2,01.

Расчетное значение критерия Фишера F = 90,107 намного превышает табличное значение критерия F табл. = 2,01, что говорит о хорошем качестве п о строенной модели (модель адекватна экспериментальным данным). Уровень значимости p = 0,00000 показывает, что построенная регрессия высоко знач и ма.

Исследуем степень корреляционной зависимости между переменными. Для этого п о строим корреляционную матрицу. Чтобы корреляционная матрица была построена при множественной регрессии, нужно установить флажок в строке Review descriptive statistics , correlations matrix в окне Multiple Regre s sions .

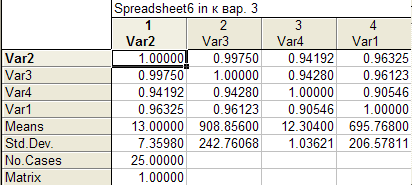
Корреляционная матрица приведена в таблице 1.4.

Из корреляционной матрицы следует, что на расходы на отдых все и с следуемые факторы оказывают значительное и примерно одинаковое влияние (коэффициенты корреляции между Var 1 и Var 2, Var 3, Var 4 равны соответственно 0,9 9975 ; 0,9 4192 ; 0, 96325 ). Из корреляционной матрицы также следует, что между факторами им е ется мультиколлинеарность (коэффициенты корр е ляции между регрессорами Var 2, Var 3, Var 4 также высоки и примерно одинаковы).

Проведем анализ остатков от регрессии.

Остатки представляю т собой разности между наблюдае мыми значениями и модел ь ными, то есть значениями, под считанными по модели с оцененными параметрами.

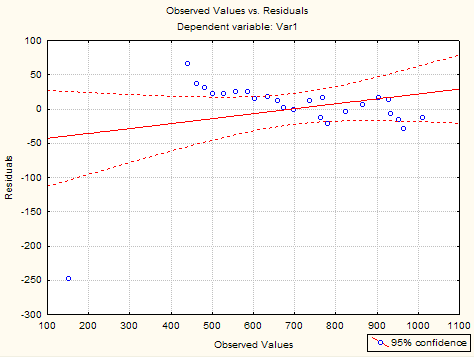
По кнопке Observed v s . residuals появится график (рис.1.1. ), который г о ворит о неслучайном р азбросе стандартных отклонений .

Рис. 1.1. Наблюдаемые переменные-остатки

Проверим остатки на наличие автокорреляции. Для этого вычислим ст а тистику Дарбина-Уотсона ( Darbin-Watson Stat ). Результаты вычисления статистики Дарбина-Уотсона привед е ны в табл. 1.5.

Из табл. 1.5 определяем наблюдаемое значение критерия Дарбина-Уотсона:

По таблице приложения 4 [1] определяем значащие точки d L и d U для 5% уровня зн а чимости.

Для m = 3 и n = 25 d L = 1,123; d U = 1,654.

Так как 4 — d U DW 4 — d L ( 2,346 2,469 ), то гипотезу об отсутствии автокорреляции мы не можем принять и не можем опровергнуть, так как значение статистики попало в зону неопределенности критерия .

Для проверки наличия гетероскедастичности воспользуемся тестом Па р ка. В Excel рассчитаем логарифмы значений e 2 , Var 2 , Var 3 и Var 4 (см. табл. 1.6).

🎦 Видео

Эконометрика. Линейная парная регрессияСкачать

Корреляционно-регрессионный анализ многомерных данных в ExcelСкачать

Статистическая функция ЛИНЕЙН. Множественная регрессия EXCEL.Скачать

Множественный регрессионный анализ в SPSS,Statistica. multiple regression in spss and StatisticaСкачать

Математика #1 | Корреляция и регрессияСкачать

РЕГРЕССИОННЫЙ АНАЛИЗ этапы | АНАЛИЗ ДАННЫХ #17Скачать

Введение Знакомство Подготовка данных для работы в статистическом пакете Statistica 10!Скачать

Что такое линейная регрессия? Душкин объяснитСкачать

Логистическая регрессия в программе StatisticaСкачать

Множественная нелинейная регрессия в StatisticaСкачать