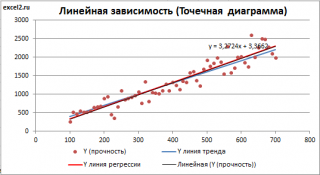
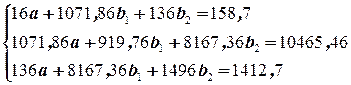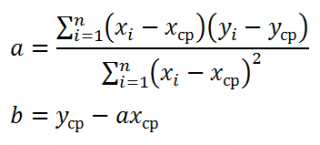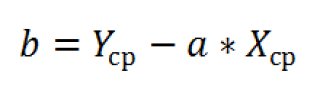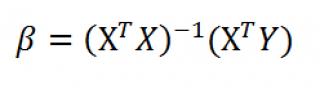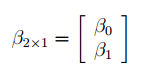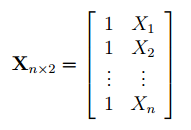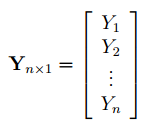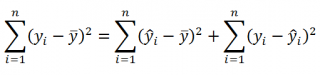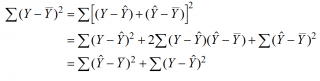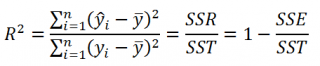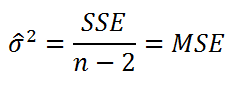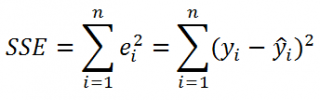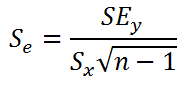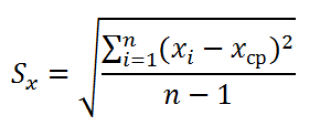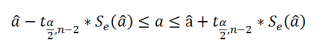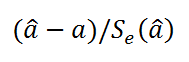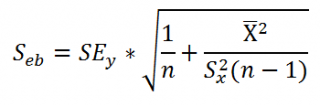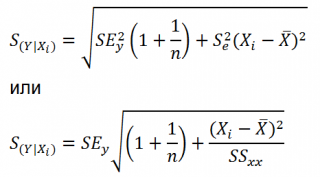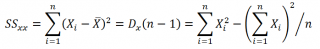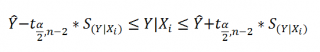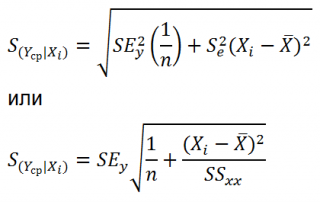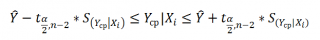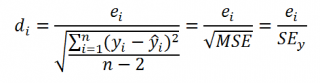В корреляционно-регрессионном анализе устранить воздействие какого-либо фактора можно, если зафиксировать воздействие этого фактора на результат и другие включенные в модель факторы. Этот прием широко используется в анализе временных рядов, когда тенденция фиксируется через включение фактора времени в модель в качестве независимой переменной.
Модель вида 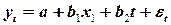
Преимущество данной модели по сравнению с методами отклонений от трендов и последовательных разностей в том, что она позволяет учесть всю информацию, содержащуюся в исходных данных, поскольку значения у, и х, есть уровни исходных временных рядов. Кроме того, модель строится по всей совокупности данных за рассматриваемый период в отличие от метода последовательных разностей, который приводит к потере числа наблюдений. Параметры а и b модели с включением фактора времени определяются обычным МНК. Расчет и интерпретацию параметров покажем на примере.
Пример 6.3. Построение модели регрессии с включением фактора времени.
Вернемся к данным предыдущих примеров. Построим уравнение регрессии, описывающее зависимость расходов на конечное потребление у, от совокупного дохода х, и фактора времени. Для расчета параметров уравнения регрессии воспользуемся обычным МНК. Система нормальных уравнений имеет вид:
Подставив требуемые суммы, получим:
Решая эту систему, получим уравнение регрессии 
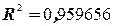


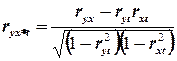

Проведем сравнительный анализ полученных результатов. Метод отклонения от тренда дает коэффициент детерминации 


Автокорреляция в остатках.
Рассмотрим уравнения регрессии вида 
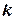
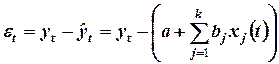
Автокорреляция остатков может быть вызвана несколькими причинами, имеющими различную природу. Во первых, иногда она связана с исходными данными и вызвана наличием ошибок измерения в значениях результативного признака. Во вторых, в ряде случаях причину автокорреляции остатков искать в формулировке модели. Модель может не включать фактор, оказывающий существенное влияние на результат, воздействие которого отражается в остатках.
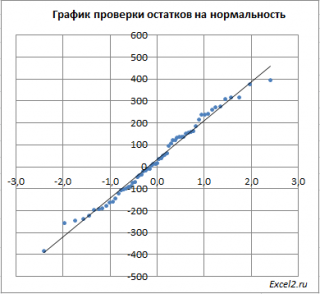
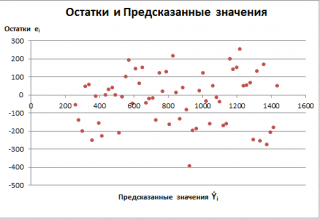
Существуют два наиболее распространенных метода определения автокорреляции остатков. Первый метод – это построение графика зависимости остатков от времени и визуальное определение наличия или отсутствия автокорреляции. Второй метод – использование критерия Дарбина-Уотсона. И расчёт величины 


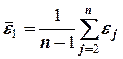
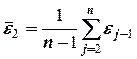

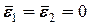
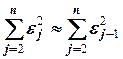
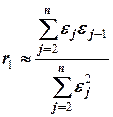

Таким образом, если в остатках существует полная положительная автокорреляция и 

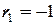
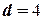
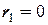


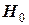

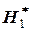


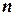
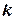


 |  |  |  |  |
Есть положительная автокорреляция остатков. 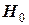 отклоняется, принимается отклоняется, принимается  . . | Зона неопределённости | Нет оснований отклонять гипотезу 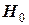 . Автокорреляция остатков отсутствует. . Автокорреляция остатков отсутствует. | Зона неопределённости | Есть отрицательная автокорреляция остатков. 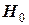 отклоняется, принимается отклоняется, принимается 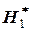 . . |
Если фактическое значение критерия Дарбина-Уотсона попадает в зону неопределённости, то на практике предполагают существование автокорреляции остатков и отклоняют гипотезу
Пример. Проверка гипотезы о наличии автокорреляции в остатках.
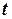 | 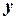 | 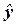 | 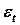 | 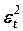 |  |  |
| 6,425 | -0,425 | 0,180625 | ||||
| 4,4 | 4,225 | 0,175 | 0,030625 | -0,6 | 0,36 | |
| 4,975 | 0,025 | 0,000625 | 0,15 | 0,0225 | ||
| 9,075 | -0,075 | 0,005625 | 0,1 | 0,01 | ||
| 7,2 | 7,175 | 0,025 | 0,000625 | -0,1 | 0,01 | |
| 4,8 | 4,975 | -0,175 | 0,030625 | 0,2 | 0,04 | |
| 5,725 | 0,275 | 0,075625 | -0,45 | 0,2025 | ||
| 9,825 | 0,175 | 0,030625 | 0,1 | 0,01 | ||
| 7,925 | 0,075 | 0,005625 | 0,1 | 0,01 | ||
| 5,6 | 5,725 | -0,125 | 0,015625 | 0,2 | 0,04 | |
| 6,4 | 6,475 | -0,075 | 0,005625 | -0,05 | 0,0025 | |
| 10,575 | 0,425 | 0,180625 | -0,5 | 0,25 | ||
| 8,675 | 0,325 | 0,105625 | 0,1 | 0,01 | ||
| 6,6 | 6,475 | 0,125 | 0,015625 | 0,2 | 0,04 | |
| 7,225 | -0,225 | 0,050625 | 0,35 | 0,1225 | ||
| 10,8 | 11,325 | -0,525 | 0,275625 | 0,3 | 0,09 | |
 | 1,01 | 1,22 |
Значение критерия Дарбина-Уотсона равно 
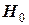

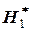
Зададим уровень значимости 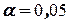

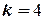
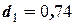

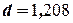


Дата добавления: 2015-10-05 ; просмотров: 3611 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
- Уравнение множественной регрессии
- Построение парной регрессионной модели
- Простая линейная регрессия в EXCEL
- Немного теории и основные понятия
- Предположения линейной регрессионной модели
- Задачи регрессионного анализа
- Оценка неизвестных параметров линейной модели (используя функции MS EXCEL)
- Оценка неизвестных параметров линейной модели (через статистики выборок)
- Оценка неизвестных параметров линейной модели (матричная форма)
- Построение линии регрессии
- Коэффициент детерминации R 2
- Стандартная ошибка регрессии
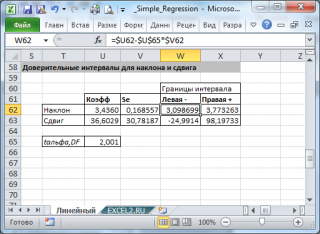
- Стандартные ошибки и доверительные интервалы для наклона и сдвига
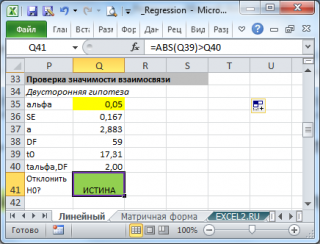
- Проверка значимости взаимосвязи переменных
- Доверительные интервалы для нового наблюдения Y и среднего значения
- Проверка адекватности линейной регрессионной модели
- 🎥 Видео
Видео:Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать

Уравнение множественной регрессии
Назначение сервиса . С помощью онлайн-калькулятора можно найти следующие показатели:
- уравнение множественной регрессии, матрица парных коэффициентов корреляции, средние коэффициенты эластичности для линейной регрессии;
- множественный коэффициент детерминации, доверительные интервалы для индивидуального и среднего значения результативного признака;
Кроме этого проводится проверка на автокорреляцию остатков и гетероскедастичность.
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
Отбор факторов обычно осуществляется в два этапа:
- теоретический анализ взаимосвязи результата и круга факторов, которые оказывают на него существенное влияние;
- количественная оценка взаимосвязи факторов с результатом. При линейной форме связи между признаками данный этап сводится к анализу корреляционной матрицы (матрицы парных линейных коэффициентов корреляции). Научно обоснованное решение задач подобного вида также осуществляется с помощью дисперсионного анализа — однофакторного, если проверяется существенность влияния того или иного фактора на рассматриваемый признак, или многофакторного в случае изучения влияния на него комбинации факторов.
Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:
- Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность.
- Каждый фактор должен быть достаточно тесно связан с результатом (т.е. коэффициент парной линейной корреляции между фактором и результатом должен быть существенным).
- Факторы не должны быть сильно коррелированы друг с другом, тем более находиться в строгой функциональной связи (т.е. они не должны быть интеркоррелированы). Разновидностью интеркоррелированности факторов является мультиколлинеарность — тесная линейная связь между факторами.
Пример . Постройте регрессионную модель с 2-мя объясняющими переменными (множественная регрессия). Определите теоретическое уравнение множественной регрессии. Оцените адекватность построенной модели.
Решение.
К исходной матрице X добавим единичный столбец, получив новую матрицу X
| 1 | 5 | 14.5 |
| 1 | 12 | 18 |
| 1 | 6 | 12 |
| 1 | 7 | 13 |
| 1 | 8 | 14 |
Матрица Y
| 9 |
| 13 |
| 16 |
| 14 |
| 21 |
Транспонируем матрицу X, получаем X T :
| 1 | 1 | 1 | 1 | 1 |
| 5 | 12 | 6 | 7 | 8 |
| 14.5 | 18 | 12 | 13 | 14 |
| Умножаем матрицы, X T X = |
|
В матрице, (X T X) число 5, лежащее на пересечении 1-й строки и 1-го столбца, получено как сумма произведений элементов 1-й строки матрицы X T и 1-го столбца матрицы X
| Умножаем матрицы, X T Y = |
|
Находим обратную матрицу (X T X) -1
| 13.99 | 0.64 | -1.3 |
| 0.64 | 0.1 | -0.0988 |
| -1.3 | -0.0988 | 0.14 |
Вектор оценок коэффициентов регрессии равен
| (X T X) -1 X T Y = y(x) = |
| * |
| = |
|
Получили оценку уравнения регрессии: Y = 34.66 + 1.97X1-2.45X2
Оценка значимости уравнения множественной регрессии осуществляется путем проверки гипотезы о равенстве нулю коэффициент детерминации рассчитанного по данным генеральной совокупности. Для ее проверки используют F-критерий Фишера.
R 2 = 1 — s 2 e/∑(yi — yср) 2 = 1 — 33.18/77.2 = 0.57
F = R 2 /(1 — R 2 )*(n — m -1)/m = 0.57/(1 — 0.57)*(5-2-1)/2 = 1.33
Табличное значение при степенях свободы k1 = 2 и k2 = n-m-1 = 5 — 2 -1 = 2, Fkp(2;2) = 19
Поскольку фактическое значение F = 1.33 Пример №2 . Приведены данные за 15 лет по темпам прироста заработной платы Y (%), производительности труда X1 (%), а также по уровню инфляции X2 (%).
| Год | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| X1 | 3,5 | 2,8 | 6,3 | 4,5 | 3,1 | 1,5 | 7,6 | 6,7 | 4,2 | 2,7 | 4,5 | 3,5 | 5,0 | 2,3 | 2,8 |
| X2 | 4,5 | 3,0 | 3,1 | 3,8 | 3,8 | 1,1 | 2,3 | 3,6 | 7,5 | 8,0 | 3,9 | 4,7 | 6,1 | 6,9 | 3,5 |
| Y | 9,0 | 6,0 | 8,9 | 9,0 | 7,1 | 3,2 | 6,5 | 9,1 | 14,6 | 11,9 | 9,2 | 8,8 | 12,0 | 12,5 | 5,7 |
Решение. Подготовим данные для вставки из MS Excel (как транспонировать таблицу для сервиса см. Задание №2) .
Включаем в отчет: Проверка общего качества уравнения множественной регрессии (F-статистика. Критерий Фишера, Проверка на наличие автокорреляции),
После нажатия на кнопку Дале получаем готовое решение.
Уравнение регрессии (оценка уравнения регрессии):
Y = 0.2706 + 0.5257X1 + 1.4798X2
Скачать.
Качество построенного уравнения регрессии проверяется с помощью критерия Фишера (п. 6 отчета).
Пример №3 .
В таблице представлены данные о ВВП, объемах потребления и инвестициях некоторых стран.
| ВВП | 16331,97 | 16763,35 | 17492,22 | 18473,83 | 19187,64 | 20066,25 | 21281,78 | 22326,86 | 23125,90 |
| Потребление в текущих ценах | 771,92 | 814,28 | 735,60 | 788,54 | 853,62 | 900,39 | 999,55 | 1076,37 | 1117,51 |
| Инвестиции в текущих ценах | 176,64 | 173,15 | 151,96 | 171,62 | 192,26 | 198,71 | 227,17 | 259,07 | 259,85 |
Решение:
Для проверки полученных расчетов используем инструменты Microsoft Excel «Анализ данных» (см. пример).
Пример №4 . На основе данных, приведенных в Приложении и соответствующих Вашему варианту (таблица 2), требуется:
- Построить уравнение множественной регрессии. При этом признак-результат и один из факторов остаются теми же, что и в первом задании. Выберите дополнительно еще один фактор из приложения 1 (границы наблюдения должны совпадать с границами наблюдения признака-результата, соответствующего Вашему варианту). При выборе фактора нужно руководствоваться его экономическим содержанием или другими подходами. Пояснить смысл параметров уравнения.
- Рассчитать частные коэффициенты эластичности. Сделать вывод.
- Определить стандартизованные коэффициенты регрессии (b-коэффициенты). Сделать вывод.
- Определить парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции; сделать выводы.
- Оценить значимость параметров уравнения регрессии с помощью t-критерия Стьюдента, а также значимость уравнения регрессии в целом с помощью общего F-критерия Фишера. Предложить окончательную модель (уравнение регрессии). Сделать выводы.
Решение. Определим вектор оценок коэффициентов регрессии. Согласно методу наименьших квадратов, вектор получается из выражения:
s = (X T X) -1 X T Y
Матрица X
| 1 | 3.9 | 10 |
| 1 | 3.9 | 14 |
| 1 | 3.7 | 15 |
| 1 | 4 | 16 |
| 1 | 3.8 | 17 |
| 1 | 4.8 | 19 |
| 1 | 5.4 | 19 |
| 1 | 4.4 | 20 |
| 1 | 5.3 | 20 |
| 1 | 6.8 | 20 |
| 1 | 6 | 21 |
| 1 | 6.4 | 22 |
| 1 | 6.8 | 22 |
| 1 | 7.2 | 25 |
| 1 | 8 | 28 |
| 1 | 8.2 | 29 |
| 1 | 8.1 | 30 |
| 1 | 8.5 | 31 |
| 1 | 9.6 | 32 |
| 1 | 9 | 36 |
Матрица Y
| 7 |
| 7 |
| 7 |
| 7 |
| 7 |
| 7 |
| 8 |
| 8 |
| 8 |
| 10 |
| 9 |
| 11 |
| 9 |
| 11 |
| 12 |
| 12 |
| 12 |
| 12 |
| 14 |
| 14 |
Матрица X T
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 3.9 | 3.9 | 3.7 | 4 | 3.8 | 4.8 | 5.4 | 4.4 | 5.3 | 6.8 | 6 | 6.4 | 6.8 | 7.2 | 8 | 8.2 | 8.1 | 8.5 | 9.6 | 9 |
| 10 | 14 | 15 | 16 | 17 | 19 | 19 | 20 | 20 | 20 | 21 | 22 | 22 | 25 | 28 | 29 | 30 | 31 | 32 | 36 |
Умножаем матрицы, (X T X)
Умножаем матрицы, (X T Y)
Находим определитель det(X T X) T = 139940.08
Находим обратную матрицу (X T X) -1
Уравнение регрессии
Y = 1.8353 + 0.9459X 1 + 0.0856X 2
Для несмещенной оценки дисперсии проделаем следующие вычисления:
Несмещенная ошибка e = Y — X*s
| 0.62 |
| 0.28 |
| 0.38 |
| 0.01 |
| 0.11 |
| -1 |
| -0.57 |
| 0.29 |
| -0.56 |
| 0.02 |
| -0.31 |
| 1.23 |
| -1.15 |
| 0.21 |
| 0.2 |
| -0.07 |
| -0.07 |
| -0.53 |
| 0.34 |
| 0.57 |
se 2 = (Y — X*s) T (Y — X*s)
Несмещенная оценка дисперсии равна
Оценка среднеквадратичного отклонения равна
Найдем оценку ковариационной матрицы вектора k = σ*(X T X) -1
| k(x) = 0.36 |
| = |
|
Дисперсии параметров модели определяются соотношением S 2 i = Kii, т.е. это элементы, лежащие на главной диагонали
С целью расширения возможностей содержательного анализа модели регрессии используются частные коэффициенты эластичности, которые определяются по формуле
Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции (от 0 до 1)
Связь между признаком Y факторами X сильная
Частные коэффициенты (или индексы) корреляции, измеряющие влияние на у фактора хi при неизменном уровне других факторов определяются по стандартной формуле линейного коэффициента корреляции — последовательно берутся пары yx1,yx2. , x1x2, x1x3.. и так далее и для каждой пары находится коэффициент корреляции
Коэффициент детерминации
R 2 = 0.97 2 = 0.95, т.е. в 95% случаев изменения х приводят к изменению y. Другими словами — точность подбора уравнения регрессии — высокая
Значимость коэффициента корреляции
По таблице Стьюдента находим Tтабл: Tтабл (n-m-1;a) = (17;0.05) = 1.74
Поскольку Tнабл Fkp, то коэффициент детерминации статистически значим и уравнение регрессии статистически надежно
Видео:Множественная регрессия в ExcelСкачать

Построение парной регрессионной модели
Рекомендации к решению контрольной работы.
Статистические данные по экономике можно получить на странице Россия в цифрах.
После определения зависимой и объясняющих переменных можно воспользоваться сервисом Множественная регрессия. Регрессионную модель с 2-мя объясняющими переменными можно построить используя матричный метод нахождения параметров уравнения регрессии или метод Крамера для нахождения параметров уравнения регрессии.
Пример №3 . Исследуется зависимость размера дивидендов y акций группы компаний от доходности акций x1, дохода компании x2 и объема инвестиций в расширение и модернизацию производства x3. Исходные данные представлены выборкой объема n=50.
Тема I. Парная линейная регрессия
Постройте парные линейные регрессии — зависимости признака y от факторов x1, x2, x3 взятых по отдельности. Для каждой объясняющей переменной:
- Постройте диаграмму рассеяния (поле корреляции). При построении выберите тип диаграммы «Точечная» (без отрезков, соединяющих точки).
- Вычислите коэффициенты уравнения выборочной парной линейной регрессии (для вычисления коэффициентов регрессии воспользуйтесь встроенной функцией ЛИНЕЙН (функция находится в категории «Статистические») или надстройкой Пакет Анализа), коэффициент детерминации, коэффициент корреляции (функция КОРЕЛЛ), среднюю ошибку аппроксимации
.
- Запишите полученное уравнение выборочной регрессии. Дайте интерпретацию найденным в предыдущем пункте значениям.
- Постройте на поле корреляции прямую линию выборочной регрессии по точкам
.
- Постройте диаграмму остатков.
- Проверьте статистическую значимость коэффициентов регрессии по критерию Стьюдента (табличное значение определите с помощью функции СТЬЮДРАСПОБР) и всего уравнения в целом по критерию Фишера (табличное значение Fтабл определите с помощью функции FРАСПОБР).
- Постройте доверительные интервалы для коэффициентов регрессии. Дайте им интерпретацию.
- Постройте прогноз для значения фактора, на 50% превышающего его среднее значение.
- Постройте доверительный интервал прогноза. Дайте ему экономическую интерпретацию.
- Оцените полученные результаты — сделайте выводы о качестве построенной модели, влиянии рассматриваемого фактора на показатель.
Тема II. Множественная линейная регрессия
1. Постройте выборочную множественную линейную регрессию показателя на все указанные факторы. Запишите полученное уравнение, дайте ему экономическую интерпретацию.
2. Определите коэффициент детерминации, дайте ему интерпретацию. Вычислите среднюю абсолютную ошибку аппроксимации 
3. Проверьте статистическую значимость каждого из коэффициентов и всего уравнения в целом.
4. Постройте диаграмму остатков.
5. Постройте доверительные интервалы коэффициентов. Для статистически значимых коэффициентов дайте интерпретации доверительных интервалов.
6. Постройте точечный прогноз значения показателя y при значениях факторов, на 50% превышающих их средние значения.
7. Постройте доверительный интервал прогноза, дайте ему экономическую интерпретацию.
8. Постройте матрицу коэффициентов выборочной корреляции между показателем и факторами. Сделайте вывод о наличии проблемы мультиколлинеарности.
9. Оцените полученные результаты — сделайте выводы о качестве построенной модели, влиянии рассматриваемых факторов на показатель.
Видео:Парная регрессия: линейная зависимостьСкачать

Простая линейная регрессия в EXCEL
history 26 января 2019 г.
- Группы статей
- Статистический анализ
Регрессия позволяет прогнозировать зависимую переменную на основании значений фактора. В MS EXCEL имеется множество функций, которые возвращают не только наклон и сдвиг линии регрессии, характеризующей линейную взаимосвязь между факторами, но и регрессионную статистику. Здесь рассмотрим простую линейную регрессию, т.е. прогнозирование на основе одного фактора.
Disclaimer : Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей Регрессионного анализа. Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения Регрессии – плохая идея.
Статья про Регрессионный анализ получилась большая, поэтому ниже для удобства приведены ее разделы:
Примечание : Если прогнозирование переменной осуществляется на основе нескольких факторов, то имеет место множественная регрессия .
Чтобы разобраться, чем может помочь MS EXCEL при проведении регрессионного анализа, напомним вкратце теорию, введем термины и обозначения, которые могут отличаться в зависимости от различных источников.
Примечание : Для тех, кому некогда, незачем или просто не хочется разбираться в теоретических выкладках предлагается сразу перейти к вычислительной части — оценке неизвестных параметров линейной модели .
Видео:Эконометрика. Линейная парная регрессияСкачать

Немного теории и основные понятия
Пусть у нас есть массив данных, представляющий собой значения двух переменных Х и Y. Причем значения переменной Х мы можем произвольно задавать (контролировать) и использовать эту переменную для предсказания значений зависимой переменной Y. Таким образом, случайной величиной является только переменная Y.
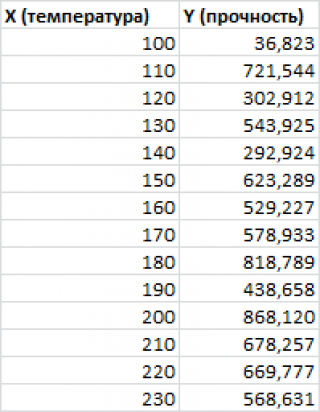
Примером такой задачи может быть производственный процесс изготовления некого волокна, причем прочность этого волокна (Y) зависит только от рабочей температуры процесса в реакторе (Х), которая задается оператором.
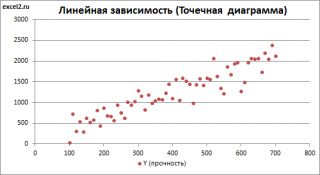
Построим диаграмму рассеяния (см. файл примера лист Линейный ), созданию которой посвящена отдельная статья . Вообще, построение диаграммы рассеяния для целей регрессионного анализа де-факто является стандартом.
СОВЕТ : Подробнее о построении различных типов диаграмм см. статьи Основы построения диаграмм и Основные типы диаграмм .
Приведенная выше диаграмма рассеяния свидетельствует о возможной линейной взаимосвязи между Y от Х: очевидно, что точки данных в основном располагаются вдоль прямой линии.
Примечание : Наличие даже такой очевидной линейной взаимосвязи не может являться доказательством о наличии причинной взаимосвязи переменных. Наличие причинной взаимосвязи не может быть доказано на основании только анализа имеющихся измерений, а должно быть обосновано с помощью других исследований, например теоретических выкладок.
Примечание : Как известно, уравнение прямой линии имеет вид Y = m * X + k , где коэффициент m отвечает за наклон линии ( slope ), k – за сдвиг линии по вертикали ( intercept ), k равно значению Y при Х=0.
Предположим, что мы можем зафиксировать переменную Х ( рабочую температуру процесса ) при некотором значении Х i и произвести несколько наблюдений переменной Y ( прочность нити ). Очевидно, что при одном и том же значении Хi мы получим различные значения Y. Это обусловлено влиянием других факторов на Y. Например, локальные колебания давления в реакторе, концентрации раствора, наличие ошибок измерения и др. Предполагается, что воздействие этих факторов имеет случайную природу и для каждого измерения имеются одинаковые условия проведения эксперимента (т.е. другие факторы не изменяются).
Полученные значения Y, при заданном Хi, будут колебаться вокруг некого значения . При увеличении количества измерений, среднее этих измерений, будет стремиться к математическому ожиданию случайной величины Y (при Х i ) равному μy(i)=Е(Y i ).
Подобные рассуждения можно привести для любого значения Хi.
Чтобы двинуться дальше, воспользуемся материалом из раздела Проверка статистических гипотез . В статье о проверке гипотезы о среднем значении генеральной совокупности в качестве нулевой гипотезы предполагалось равенство неизвестного значения μ заданному μ0.
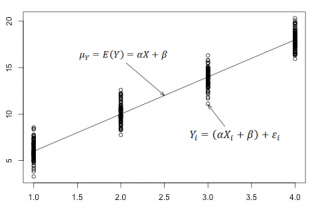
В нашем случае простой линейной регрессии в качестве нулевой гипотезы предположим, что между переменными μy(i) и Хi существует линейная взаимосвязь μ y(i) =α* Х i +β. Уравнение μ y(i) =α* Х i +β можно переписать в обобщенном виде (для всех Х и μ y ) как μ y =α* Х +β.
Для наглядности проведем прямую линию соединяющую все μy(i).
Данная линия называется регрессионной линией генеральной совокупности (population regression line), параметры которой ( наклон a и сдвиг β ) нам не известны (по аналогии с гипотезой о среднем значении генеральной совокупности , где нам было неизвестно истинное значение μ).
Теперь сделаем переход от нашего предположения, что μy=a* Х + β , к предсказанию значения случайной переменной Y в зависимости от значения контролируемой переменной Х. Для этого уравнение связи двух переменных запишем в виде Y=a*X+β+ε, где ε — случайная ошибка, которая отражает суммарный эффект влияния других факторов на Y (эти «другие» факторы не участвуют в нашей модели). Напомним, что т.к. переменная Х фиксирована, то ошибка ε определяется только свойствами переменной Y.
Уравнение Y=a*X+b+ε называют линейной регрессионной моделью . Часто Х еще называют независимой переменной (еще предиктором и регрессором , английский термин predictor , regressor ), а Y – зависимой (или объясняемой , response variable ). Так как регрессор у нас один, то такая модель называется простой линейной регрессионной моделью ( simple linear regression model ). α часто называют коэффициентом регрессии.
Предположения линейной регрессионной модели перечислены в следующем разделе.
Видео:Эконометрика Линейная регрессия и корреляцияСкачать

Предположения линейной регрессионной модели
Чтобы модель линейной регрессии Yi=a*Xi+β+ε i была адекватной — требуется:
- Ошибки ε i должны быть независимыми переменными;
- При каждом значении Xi ошибки ε i должны быть иметь нормальное распределение (также предполагается равенство нулю математического ожидания, т.е. Е[ε i ]=0);
- При каждом значении Xi ошибки ε i должны иметь равные дисперсии (обозначим ее σ 2 ).
Примечание : Последнее условие называется гомоскедастичность — стабильность, гомогенность дисперсии случайной ошибки e. Т.е. дисперсия ошибки σ 2 не должна зависеть от значения Xi.
Используя предположение о равенстве математического ожидания Е[ε i ]=0 покажем, что μy(i)=Е[Yi]:
Е[Yi]= Е[a*Xi+β+ε i ]= Е[a*Xi+β]+ Е[ε i ]= a*Xi+β= μy(i), т.к. a, Xi и β постоянные значения.
Дисперсия случайной переменной Y равна дисперсии ошибки ε, т.е. VAR(Y)= VAR(ε)=σ 2 . Это является следствием, что все значения переменной Х являются const, а VAR(ε)=VAR(ε i ).
Видео:Множественная регрессияСкачать

Задачи регрессионного анализа
Для проверки гипотезы о линейной взаимосвязи переменной Y от X делают выборку из генеральной совокупности (этой совокупности соответствует регрессионная линия генеральной совокупности , т.е. μy=a* Х +β). Выборка будет состоять из n точек, т.е. из n пар значений .
На основании этой выборки мы можем вычислить оценки наклона a и сдвига β, которые обозначим соответственно a и b . Также часто используются обозначения â и b̂.
Далее, используя эти оценки, мы также можем проверить гипотезу: имеется ли линейная связь между X и Y статистически значимой?
Первая задача регрессионного анализа – оценка неизвестных параметров ( estimation of the unknown parameters ). Подробнее см. раздел Оценки неизвестных параметров модели .
Вторая задача регрессионного анализа – Проверка адекватности модели ( model adequacy checking ).
Примечание : Оценки параметров модели обычно вычисляются методом наименьших квадратов (МНК), которому посвящена отдельная статья .
Видео:Математика #1 | Корреляция и регрессияСкачать

Оценка неизвестных параметров линейной модели (используя функции MS EXCEL)
Неизвестные параметры простой линейной регрессионной модели Y=a*X+β+ε оценим с помощью метода наименьших квадратов (в статье про МНК подробно описано этот метод ).
Для вычисления параметров линейной модели методом МНК получены следующие выражения:
Таким образом, мы получим уравнение прямой линии Y= a *X+ b , которая наилучшим образом аппроксимирует имеющиеся данные.
Примечание : В статье про метод наименьших квадратов рассмотрены случаи аппроксимации линейной и квадратичной функцией , а также степенной , логарифмической и экспоненциальной функцией .
Оценку параметров в MS EXCEL можно выполнить различными способами:
Сначала рассмотрим функции НАКЛОН() , ОТРЕЗОК() и ЛИНЕЙН() .
Пусть значения Х и Y находятся соответственно в диапазонах C 23: C 83 и B 23: B 83 (см. файл примера внизу статьи).
Примечание : Значения двух переменных Х и Y можно сгенерировать, задав тренд и величину случайного разброса (см. статью Генерация данных для линейной регрессии в MS EXCEL ).
В MS EXCEL наклон прямой линии а ( оценку коэффициента регрессии ), можно найти по методу МНК с помощью функции НАКЛОН() , а сдвиг b ( оценку постоянного члена или константы регрессии ), с помощью функции ОТРЕЗОК() . В английской версии это функции SLOPE и INTERCEPT соответственно.
Аналогичный результат можно получить с помощью функции ЛИНЕЙН() , английская версия LINEST (см. статью об этой функции ).
Формула =ЛИНЕЙН(C23:C83;B23:B83) вернет наклон а . А формула = ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2) — сдвиг b . Здесь требуются пояснения.
Функция ЛИНЕЙН() имеет 4 аргумента и возвращает целый массив значений:
ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика])
Если 4-й аргумент статистика имеет значение ЛОЖЬ или опущен, то функция ЛИНЕЙН() возвращает только оценки параметров модели: a и b .
Примечание : Остальные значения, возвращаемые функцией ЛИНЕЙН() , нам потребуются при вычислении стандартных ошибок и для проверки значимости регрессии . В этом случае аргумент статистика должен иметь значение ИСТИНА.
Чтобы вывести сразу обе оценки:
- в одной строке необходимо выделить 2 ячейки,
- ввести формулу в Строке формул
- нажать CTRL+SHIFT+ENTER (см. статью про формулы массива ).
Если в Строке формул выделить формулу = ЛИНЕЙН(C23:C83;B23:B83) и нажать клавишу F9 , то мы увидим что-то типа . Это как раз значения a и b . Как видно, оба значения разделены точкой с запятой «;», что свидетельствует, что функция вернула значения «в нескольких ячейках одной строки».
Если требуется вывести параметры линии не в одной строке, а одном столбце (ячейки друг под другом), то используйте формулу = ТРАНСП(ЛИНЕЙН(C23:C83;B23:B83)) . При этом выделять нужно 2 ячейки в одном столбце. Если теперь выделить новую формулу и нажать клавишу F9, то мы увидим что 2 значения разделены двоеточием «:», что означает, что значения выведены в столбец (функция ТРАНСП() транспонировала строку в столбец ).
Чтобы разобраться в этом подробнее необходимо ознакомиться с формулами массива .
Чтобы не связываться с вводом формул массива , можно использовать функцию ИНДЕКС() . Формула = ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);1) или просто ЛИНЕЙН(C23:C83;B23:B83) вернет параметр, отвечающий за наклон линии, т.е. а . Формула =ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2) вернет параметр b .
Видео:Тема по SPSS: множественная линейная регрессия - одновременное включение всех переменных в модель.Скачать

Оценка неизвестных параметров линейной модели (через статистики выборок)
Наклон линии, т.е. коэффициент а , можно также вычислить через коэффициент корреляции и стандартные отклонения выборок :
= КОРРЕЛ(B23:B83;C23:C83) *(СТАНДОТКЛОН.В(C23:C83)/ СТАНДОТКЛОН.В(B23:B83))
Вышеуказанная формула математически эквивалентна отношению ковариации выборок Х и Y и дисперсии выборки Х:
И, наконец, запишем еще одну формулу для нахождения сдвига b . Воспользуемся тем фактом, что линия регрессии проходит через точку средних значений переменных Х и Y.
Вычислив средние значения и подставив в формулу ранее найденный наклон а , получим сдвиг b .
Видео:Линейная регрессияСкачать

Оценка неизвестных параметров линейной модели (матричная форма)
Также параметры линии регрессии можно найти в матричной форме (см. файл примера лист Матричная форма ).
В формуле символом β обозначен столбец с искомыми параметрами модели: β0 (сдвиг b ), β1 (наклон a ).
Матрица Х равна:
Матрица Х называется регрессионной матрицей или матрицей плана . Она состоит из 2-х столбцов и n строк, где n – количество точек данных. Первый столбец — столбец единиц, второй – значения переменной Х.
Матрица Х T – это транспонированная матрица Х . Она состоит соответственно из n столбцов и 2-х строк.
В формуле символом Y обозначен столбец значений переменной Y.
Чтобы перемножить матрицы используйте функцию МУМНОЖ() . Чтобы найти обратную матрицу используйте функцию МОБР() .
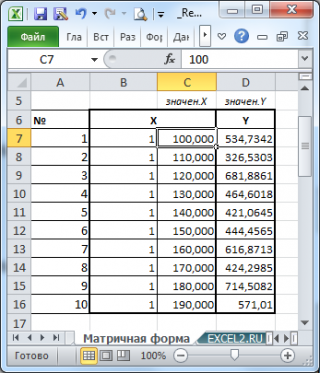
Пусть дан массив значений переменных Х и Y (n=10, т.е.10 точек).
Слева от него достроим столбец с 1 для матрицы Х.
и введя ее как формулу массива в 2 ячейки, получим оценку параметров модели.
Красота применения матричной формы полностью раскрывается в случае множественной регрессии .
Видео:Регрессия - как строить и интерпретировать. Примеры линейной и множественной регрессии.Скачать

Построение линии регрессии
Для отображения линии регрессии построим сначала диаграмму рассеяния , на которой отобразим все точки (см. начало статьи ).
Для построения прямой линии используйте вычисленные выше оценки параметров модели a и b (т.е. вычислите у по формуле y = a * x + b ) или функцию ТЕНДЕНЦИЯ() .
Формула = ТЕНДЕНЦИЯ($C$23:$C$83;$B$23:$B$83;B23) возвращает расчетные (прогнозные) значения ŷi для заданного значения Хi из столбца В2 .
Примечание : Линию регрессии можно также построить с помощью функции ПРЕДСКАЗ() . Эта функция возвращает прогнозные значения ŷi, но, в отличие от функции ТЕНДЕНЦИЯ() работает только в случае одного регрессора. Функция ТЕНДЕНЦИЯ() может быть использована и в случае множественной регрессии (в этом случае 3-й аргумент функции должен быть ссылкой на диапазон, содержащий все значения Хi для выбранного наблюдения i).
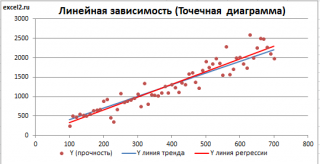
Как видно из диаграммы выше линия тренда и линия регрессии не обязательно совпадают: отклонения точек от линии тренда случайны, а МНК лишь подбирает линию наиболее точно аппроксимирующую случайные точки данных.
Линию регрессии можно построить и с помощью встроенных средств диаграммы, т.е. с помощью инструмента Линия тренда. Для этого выделите диаграмму, в меню выберите вкладку Макет , в группе Анализ нажмите Линия тренда , затем Линейное приближение. В диалоговом окне установите галочку Показывать уравнение на диаграмме (подробнее см. в статье про МНК ).
Построенная таким образом линия, разумеется, должна совпасть с ранее построенной нами линией регрессии, а параметры уравнения a и b должны совпасть с параметрами уравнения отображенными на диаграмме.
Примечание: Для того, чтобы вычисленные параметры уравнения a и b совпадали с параметрами уравнения на диаграмме, необходимо, чтобы тип у диаграммы был Точечная, а не График , т.к. тип диаграммы График не использует значения Х, а вместо значений Х используется последовательность 1; 2; 3; . Именно эти значения и берутся при расчете параметров линии тренда . Убедиться в этом можно если построить диаграмму График (см. файл примера ), а значения Хнач и Хшаг установить равным 1. Только в этом случае параметры уравнения на диаграмме совпадут с a и b .
Видео:Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать

Коэффициент детерминации R 2
Коэффициент детерминации R 2 показывает насколько полезна построенная нами линейная регрессионная модель .
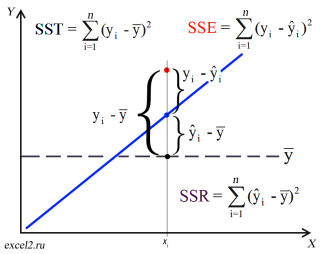
Предположим, что у нас есть n значений переменной Y и мы хотим предсказать значение yi, но без использования значений переменной Х (т.е. без построения регрессионной модели ). Очевидно, что лучшей оценкой для yi будет среднее значение ȳ. Соответственно, ошибка предсказания будет равна (yi — ȳ).
Примечание : Далее будет использована терминология и обозначения дисперсионного анализа .
После построения регрессионной модели для предсказания значения yi мы будем использовать значение ŷi=a*xi+b. Ошибка предсказания теперь будет равна (yi — ŷi).
Теперь с помощью диаграммы сравним ошибки предсказания полученные без построения модели и с помощью модели.
Очевидно, что используя регрессионную модель мы уменьшили первоначальную (полную) ошибку (yi — ȳ) на значение (ŷi — ȳ) до величины (yi — ŷi).
(yi — ŷi) – это оставшаяся, необъясненная ошибка.
Очевидно, что все три ошибки связаны выражением:
(yi — ȳ)= (ŷi — ȳ) + (yi — ŷi)
Можно показать, что в общем виде справедливо следующее выражение:
или в других, общепринятых в зарубежной литературе, обозначениях:
Total Sum of Squares = Regression Sum of Squares + Error Sum of Squares
Примечание : SS — Sum of Squares — Сумма Квадратов.
Как видно из формулы величины SST, SSR, SSE имеют размерность дисперсии (вариации) и соответственно описывают разброс (изменчивость): Общую изменчивость (Total variation), Изменчивость объясненную моделью (Explained variation) и Необъясненную изменчивость (Unexplained variation).
По определению коэффициент детерминации R 2 равен:
R 2 = Изменчивость объясненная моделью / Общая изменчивость.
Этот показатель равен квадрату коэффициента корреляции и в MS EXCEL его можно вычислить с помощью функции КВПИРСОН() или ЛИНЕЙН() :
R 2 принимает значения от 0 до 1 (1 соответствует идеальной линейной зависимости Y от Х). Однако, на практике малые значения R2 вовсе не обязательно указывают, что переменную Х нельзя использовать для прогнозирования переменной Y. Малые значения R2 могут указывать на нелинейность связи или на то, что поведение переменной Y объясняется не только Х, но и другими факторами.
Видео:Парная нелинейная регрессияСкачать

Стандартная ошибка регрессии
Стандартная ошибка регрессии ( Standard Error of a regression ) показывает насколько велика ошибка предсказания значений переменной Y на основании значений Х. Отдельные значения Yi мы можем предсказывать лишь с точностью +/- несколько значений (обычно 2-3, в зависимости от формы распределения ошибки ε).
Теперь вспомним уравнение линейной регрессионной модели Y=a*X+β+ε. Ошибка ε имеет случайную природу, т.е. является случайной величиной и поэтому имеет свою функцию распределения со средним значением μ и дисперсией σ 2 .
Оценив значение дисперсии σ 2 и вычислив из нее квадратный корень – получим Стандартную ошибку регрессии. Чем точки наблюдений на диаграмме рассеяния ближе находятся к прямой линии, тем меньше Стандартная ошибка.
Примечание : Вспомним , что при построении модели предполагается, что среднее значение ошибки ε равно 0, т.е. E[ε]=0.
Оценим дисперсию σ 2 . Помимо вычисления Стандартной ошибки регрессии эта оценка нам потребуется в дальнейшем еще и при построении доверительных интервалов для оценки параметров регрессии a и b .
Для оценки дисперсии ошибки ε используем остатки регрессии — разности между имеющимися значениями yi и значениями, предсказанными регрессионной моделью ŷ. Чем лучше регрессионная модель согласуется с данными (точки располагается близко к прямой линии), тем меньше величина остатков.
Для оценки дисперсии σ 2 используют следующую формулу:
где SSE – сумма квадратов значений ошибок модели ε i =yi — ŷi ( Sum of Squared Errors ).
SSE часто обозначают и как SSres – сумма квадратов остатков ( Sum of Squared residuals ).
Оценка дисперсии s 2 также имеет общепринятое обозначение MSE (Mean Square of Errors), т.е. среднее квадратов ошибок или MSRES (Mean Square of Residuals), т.е. среднее квадратов остатков . Хотя правильнее говорить сумме квадратов остатков, т.к. ошибка чаще ассоциируется с ошибкой модели ε, которая является непрерывной случайной величиной. Но, здесь мы будем использовать термины SSE и MSE, предполагая, что речь идет об остатках.
Примечание : Напомним, что когда мы использовали МНК для нахождения параметров модели, то критерием оптимизации была минимизация именно SSE (SSres). Это выражение представляет собой сумму квадратов расстояний между наблюденными значениями yi и предсказанными моделью значениями ŷi, которые лежат на линии регрессии.
Математическое ожидание случайной величины MSE равно дисперсии ошибки ε, т.е. σ 2 .
Чтобы понять почему SSE выбрана в качестве основы для оценки дисперсии ошибки ε, вспомним, что σ 2 является также дисперсией случайной величины Y (относительно среднего значения μy, при заданном значении Хi). А т.к. оценкой μy является значение ŷi = a * Хi + b (значение уравнения регрессии при Х= Хi), то логично использовать именно SSE в качестве основы для оценки дисперсии σ 2 . Затем SSE усредняется на количество точек данных n за вычетом числа 2. Величина n-2 – это количество степеней свободы ( df – degrees of freedom ), т.е. число параметров системы, которые могут изменяться независимо (вспомним, что у нас в этом примере есть n независимых наблюдений переменной Y). В случае простой линейной регрессии число степеней свободы равно n-2, т.к. при построении линии регрессии было оценено 2 параметра модели (на это было «потрачено» 2 степени свободы ).
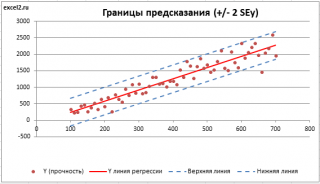
Итак, как сказано было выше, квадратный корень из s 2 имеет специальное название Стандартная ошибка регрессии ( Standard Error of a regression ) и обозначается SEy. SEy показывает насколько велика ошибка предсказания. Отдельные значения Y мы можем предсказывать с точностью +/- несколько значений SEy (см. этот раздел ). Если ошибки предсказания ε имеют нормальное распределение , то примерно 2/3 всех предсказанных значений будут на расстоянии не больше SEy от линии регрессии . SEy имеет размерность переменной Y и откладывается по вертикали. Часто на диаграмме рассеяния строят границы предсказания соответствующие +/- 2 SEy (т.е. 95% точек данных будут располагаться в пределах этих границ).
В MS EXCEL стандартную ошибку SEy можно вычислить непосредственно по формуле:
= КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))
или с помощью функции ЛИНЕЙН() :
Примечание : Подробнее о функции ЛИНЕЙН() см. эту статью .
Видео:Множественная регрессия в Excel и мультиколлинеарностьСкачать

Стандартные ошибки и доверительные интервалы для наклона и сдвига
В разделе Оценка неизвестных параметров линейной модели мы получили точечные оценки наклона а и сдвига b . Так как эти оценки получены на основе случайных величин (значений переменных Х и Y), то эти оценки сами являются случайными величинами и соответственно имеют функцию распределения со средним значением и дисперсией . Но, чтобы перейти от точечных оценок к интервальным , необходимо вычислить соответствующие стандартные ошибки (т.е. стандартные отклонения ).
Стандартная ошибка коэффициента регрессии a вычисляется на основании стандартной ошибки регрессии по следующей формуле:
где Sx – стандартное отклонение величины х, вычисляемое по формуле:
где Sey – стандартная ошибка регрессии, т.е. ошибка предсказания значения переменой Y ( см. выше ).
В MS EXCEL стандартную ошибку коэффициента регрессии Se можно вычислить впрямую по вышеуказанной формуле:
= КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))/ СТАНДОТКЛОН.В(B23:B83) /КОРЕНЬ(СЧЁТ(B23:B83) -1)
или с помощью функции ЛИНЕЙН() :
Формулы приведены в файле примера на листе Линейный в разделе Регрессионная статистика .
Примечание : Подробнее о функции ЛИНЕЙН() см. эту статью .
При построении двухстороннего доверительного интервала для коэффициента регрессии его границы определяются следующим образом:
где — квантиль распределения Стьюдента с n-2 степенями свободы. Величина а с «крышкой» является другим обозначением наклона а .
Например для уровня значимости альфа=0,05, можно вычислить с помощью формулы =СТЬЮДЕНТ.ОБР.2Х(0,05;n-2)
Вышеуказанная формула следует из того факта, что если ошибки регрессии распределены нормально и независимо, то выборочное распределение случайной величины
является t-распределением Стьюдента с n-2 степенью свободы (то же справедливо и для наклона b ).
Примечание : Подробнее о построении доверительных интервалов в MS EXCEL можно прочитать в этой статье Доверительные интервалы в MS EXCEL .
В результате получим, что найденный доверительный интервал с вероятностью 95% (1-0,05) накроет истинное значение коэффициента регрессии. Здесь мы считаем, что коэффициент регрессии a имеет распределение Стьюдента с n-2 степенями свободы (n – количество наблюдений, т.е. пар Х и Y).
Примечание : Подробнее о построении доверительных интервалов с использованием t-распределения см. статью про построение доверительных интервалов для среднего .
Стандартная ошибка сдвига b вычисляется по следующей формуле:
В MS EXCEL стандартную ошибку сдвига Seb можно вычислить с помощью функции ЛИНЕЙН() :
При построении двухстороннего доверительного интервала для сдвига его границы определяются аналогичным образом как для наклона : b +/- t*Seb.
Видео:Эконометрика. Множественная регрессия и корреляция.Скачать

Проверка значимости взаимосвязи переменных
Когда мы строим модель Y=αX+β+ε мы предполагаем, что между Y и X существует линейная взаимосвязь. Однако, как это иногда бывает в статистике, можно вычислять параметры связи даже тогда, когда в действительности она не существует, и обусловлена лишь случайностью.
Единственный вариант, когда Y не зависит X (в рамках модели Y=αX+β+ε), возможен, когда коэффициент регрессии a равен 0.
Чтобы убедиться, что вычисленная нами оценка наклона прямой линии не обусловлена лишь случайностью (не случайно отлична от 0), используют проверку гипотез . В качестве нулевой гипотезы Н 0 принимают, что связи нет, т.е. a=0. В качестве альтернативной гипотезы Н 1 принимают, что a 0.
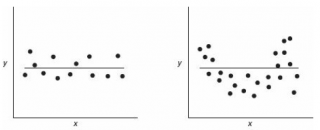
Ниже на рисунках показаны 2 ситуации, когда нулевую гипотезу Н 0 не удается отвергнуть.
На левой картинке отсутствует любая зависимость между переменными, на правой – связь между ними нелинейная, но при этом коэффициент линейной корреляции равен 0.
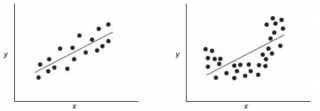
Ниже — 2 ситуации, когда нулевая гипотеза Н 0 отвергается.
На левой картинке очевидна линейная зависимость, на правой — зависимость нелинейная, но коэффициент корреляции не равен 0 (метод МНК вычисляет показатели наклона и сдвига просто на основании значений выборки).
Для проверки гипотезы нам потребуется:
- Установить уровень значимости , пусть альфа=0,05;
- Рассчитать с помощью функции ЛИНЕЙН() стандартное отклонение Se для коэффициента регрессии (см. предыдущий раздел );
- Рассчитать число степеней свободы: DF=n-2 или по формуле = ИНДЕКС(ЛИНЕЙН(C24:C84;B24:B84;;ИСТИНА);4;2)
- Вычислить значение тестовой статистики t 0 =a/S e , которая имеет распределение Стьюдента с числом степеней свободы DF=n-2;
- Сравнить значение тестовой статистики |t0| с пороговым значением t альфа ,n-2. Если значение тестовой статистики больше порогового значения, то нулевая гипотеза отвергается ( наклон не может быть объяснен лишь случайностью при заданном уровне альфа) либо
- вычислить p-значение и сравнить его с уровнем значимости .
В файле примера приведен пример проверки гипотезы:
Изменяя наклон тренда k (ячейка В8 ) можно убедиться, что при малых углах тренда (например, 0,05) тест часто показывает, что связь между переменными случайна. При больших углах (k>1), тест практически всегда подтверждает значимость линейной связи между переменными.
Примечание : Проверка значимости взаимосвязи эквивалентна проверке статистической значимости коэффициента корреляции . В файле примера показана эквивалентность обоих подходов. Также проверку значимости можно провести с помощью процедуры F-тест .
Видео:Уравнение парной линейной регрессии с помощью Анализа ДанныхСкачать

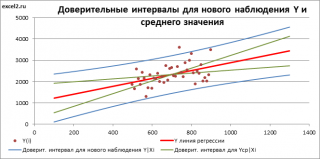
Доверительные интервалы для нового наблюдения Y и среднего значения
Вычислив параметры простой линейной регрессионной модели Y=aX+β+ε мы получили точечную оценку значения нового наблюдения Y при заданном значении Хi, а именно: Ŷ= a * Хi + b
Ŷ также является точечной оценкой для среднего значения Yi при заданном Хi. Но, при построении доверительных интервалов используются различные стандартные ошибки .
Стандартная ошибка нового наблюдения Y при заданном Хi учитывает 2 источника неопределенности:
- неопределенность связанную со случайностью оценок параметров модели a и b ;
- случайность ошибки модели ε.
Учет этих неопределенностей приводит к стандартной ошибке S(Y|Xi), которая рассчитывается с учетом известного значения Xi.
где SS xx – сумма квадратов отклонений от среднего значений переменной Х:
В MS EXCEL 2010 нет функции, которая бы рассчитывала эту стандартную ошибку , поэтому ее необходимо рассчитывать по вышеуказанным формулам.
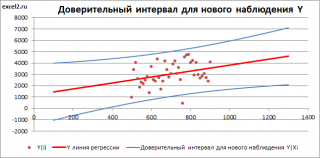
Доверительный интервал или Интервал предсказания для нового наблюдения (Prediction Interval for a New Observation) построим по схеме показанной в разделе Проверка значимости взаимосвязи переменных (см. файл примера лист Интервалы ). Т.к. границы интервала зависят от значения Хi (точнее от расстояния Хi до среднего значения Х ср ), то интервал будет постепенно расширяться при удалении от Х ср .
Границы доверительного интервала для нового наблюдения рассчитываются по формуле:
Аналогичным образом построим доверительный интервал для среднего значения Y при заданном Хi (Confidence Interval for the Mean of Y). В этом случае доверительный интервал будет уже, т.к. средние значения имеют меньшую изменчивость по сравнению с отдельными наблюдениями ( средние значения, в рамках нашей линейной модели Y=aX+β+ε, не включают ошибку ε).
Стандартная ошибка S(Yср|Xi) вычисляется по практически аналогичным формулам как и стандартная ошибка для нового наблюдения:
Как видно из формул, стандартная ошибка S(Yср|Xi) меньше стандартной ошибки S(Y|Xi) для индивидуального значения .
Границы доверительного интервала для среднего значения рассчитываются по формуле:
Видео:Что такое линейная регрессия? Душкин объяснитСкачать

Проверка адекватности линейной регрессионной модели
Модель адекватна, когда все предположения, лежащие в ее основе, выполнены (см. раздел Предположения линейной регрессионной модели ).
Проверка адекватности модели в основном основана на исследовании остатков модели (model residuals), т.е. значений ei=yi – ŷi для каждого Хi. В рамках простой линейной модели n остатков имеют только n-2 связанных с ними степеней свободы . Следовательно, хотя, остатки не являются независимыми величинами, но при достаточно большом n это не оказывает какого-либо влияния на проверку адекватности модели.
Чтобы проверить предположение о нормальности распределения ошибок строят график проверки на нормальность (Normal probability Plot).
В файле примера на листе Адекватность построен график проверки на нормальность . В случае нормального распределения значения остатков должны быть близки к прямой линии.
Так как значения переменной Y мы генерировали с помощью тренда , вокруг которого значения имели нормальный разброс, то ожидать сюрпризов не приходится – значения остатков располагаются вблизи прямой.
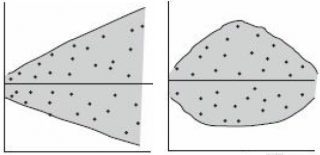
Также при проверке модели на адекватность часто строят график зависимости остатков от предсказанных значений Y. Если точки не демонстрируют характерных, так называемых «паттернов» (шаблонов) типа вор о нок или другого неравномерного распределения, в зависимости от значений Y, то у нас нет очевидных доказательств неадекватности модели.
В нашем случае точки располагаются примерно равномерно.
Часто при проверке адекватности модели вместо остатков используют нормированные остатки. Как показано в разделе Стандартная ошибка регрессии оценкой стандартного отклонения ошибок является величина SEy равная квадратному корню из величины MSE. Поэтому логично нормирование остатков проводить именно на эту величину.
SEy можно вычислить с помощью функции ЛИНЕЙН() :
Иногда нормирование остатков производится на величину стандартного отклонения остатков (это мы увидим в статье об инструменте Регрессия , доступного в надстройке MS EXCEL Пакет анализа ), т.е. по формуле:
Вышеуказанное равенство приблизительное, т.к. среднее значение остатков близко, но не обязательно точно равно 0.
🎥 Видео
РЕГРЕССИОННЫЙ АНАЛИЗ общая идея | АНАЛИЗ ДАННЫХ #16Скачать

Критерий Стьюдента и Фишера в Excel, проверка уравнения множественной регрессии в ExcelСкачать

Эконометрика. Построение модели множественной регрессии в Excel. Часть 1.Скачать

Нелинейная регрессия в MS Excel. Как подобрать уравнение регрессии? Некорректное значение R^2Скачать