Вместе с этим калькулятором также используют следующие:
Уравнение множественной регрессии
- Виды нелинейной регрессии
- Простая линейная и полиномиальная регрессия
- Оглавление
- Часть 1: извлечение данных, визуализация и предварительный анализ
- Часть 2: Простая линейная регрессия
- Часть 3: Квадратичный и полиномиальный регрессионный анализ высокой степени
- Часть 4. Сегментируйте данные в обучении и тестировании
- Часть 5. Тестовые модели по типу регрессии
- Вывод:
- 5 видов регрессии и их свойства
- Линейная регрессия
- Полиномиальная регрессия
- Гребневая (ридж) регрессия
- Регрессия по методу «лассо»
- Регрессия «эластичная сеть»
- Вывод
- 📹 Видео
Видео:Что такое полиномиальная регрессия? Душкин объяснитСкачать

Виды нелинейной регрессии
| Вид | Класс нелинейных моделей |
| Нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам |
| Нелинейные по оцениваемым параметрам |
Здесь ε — случайная ошибка (отклонение, возмущение), отражающая влияние всех неучтенных факторов.
Уравнению регрессии первого порядка — это уравнение парной линейной регрессии.
Уравнение регрессии второго порядка это полиномальное уравнение регрессии второго порядка: y = a + bx + cx 2 .
Уравнение регрессии третьего порядка соответственно полиномальное уравнение регрессии третьего порядка: y = a + bx + cx 2 + dx 3 .
Чтобы привести нелинейные зависимости к линейной используют методы линеаризации (см. метод выравнивания):
- Замена переменных.
- Логарифмирование обеих частей уравнения.
- Комбинированный.
| y = f(x) | Преобразование | Метод линеаризации |
| y = b x a | Y = ln(y); X = ln(x) | Логарифмирование |
| y = b e ax | Y = ln(y); X = x | Комбинированный |
| y = 1/(ax+b) | Y = 1/y; X = x | Замена переменных |
| y = x/(ax+b) | Y = x/y; X = x | Замена переменных. Пример |
| y = aln(x)+b | Y = y; X = ln(x) | Комбинированный |
| y = a + bx + cx 2 | x1 = x; x2 = x 2 | Замена переменных |
| y = a + bx + cx 2 + dx 3 | x1 = x; x2 = x 2 ; x3 = x 3 | Замена переменных |
| y = a + b/x | x1 = 1/x | Замена переменных |
| y = a + sqrt(x)b | x1 = sqrt(x) | Замена переменных |
Пример . По данным, взятым из соответствующей таблицы, выполнить следующие действия:
- Построить поле корреляции и сформулировать гипотезу о форме связи.
- Рассчитать параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессии.
- Оценить тесноту связи с помощью показателей корреляции и детерминации.
- Дать с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
- Оценить с помощью средней ошибки аппроксимации качество уравнений.
- Оценить с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования. По значениям характеристик, рассчитанных в пп. 4, 5 и данном пункте, выбрать лучшее уравнение регрессии и дать его обоснование.
- Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 15% от его среднего уровня. Определить доверительный интервал прогноза для уровня значимости α=0,05 .
- Оценить полученные результаты, выводы оформить в аналитической записке.
| Год | Фактическое конечное потребление домашних хозяйств (в текущих ценах), млрд. руб. (1995 г. — трлн. руб.), y | Среднедушевые денежные доходы населения (в месяц), руб. (1995 г. — тыс. руб.), х |
| 1995 | 872 | 515,9 |
| 2000 | 3813 | 2281,1 |
| 2001 | 5014 | 3062 |
| 2002 | 6400 | 3947,2 |
| 2003 | 7708 | 5170,4 |
| 2004 | 9848 | 6410,3 |
| 2005 | 12455 | 8111,9 |
| 2006 | 15284 | 10196 |
| 2007 | 18928 | 12602,7 |
| 2008 | 23695 | 14940,6 |
| 2009 | 25151 | 16856,9 |
Решение. В калькуляторе последовательно выбираем виды нелинейной регрессии. Получим таблицу следующего вида.
Экспоненциальное уравнение регрессии имеет вид y = a e bx
После линеаризации получим: ln(y) = ln(a) + bx
Получаем эмпирические коэффициенты регрессии: b = 0.000162, a = 7.8132
Уравнение регрессии: y = e 7.81321500 e 0.000162x = 2473.06858e 0.000162x
Степенное уравнение регрессии имеет вид y = a x b
После линеаризации получим: ln(y) = ln(a) + b ln(x)
Эмпирические коэффициенты регрессии: b = 0.9626, a = 0.7714
Уравнение регрессии: y = e 0.77143204 x 0.9626 = 2.16286x 0.9626
Гиперболическое уравнение регрессии имеет вид y = b/x + a + ε
После линеаризации получим: y=bx + a
Эмпирические коэффициенты регрессии: b = 21089190.1984, a = 4585.5706
Эмпирическое уравнение регрессии: y = 21089190.1984 / x + 4585.5706
Логарифмическое уравнение регрессии имеет вид y = b ln(x) + a + ε
Эмпирические коэффициенты регрессии: b = 7142.4505, a = -49694.9535
Уравнение регрессии: y = 7142.4505 ln(x) — 49694.9535
Видео:Что такое линейная регрессия? Душкин объяснитСкачать

Простая линейная и полиномиальная регрессия
Дата публикации Jun 15, 2019
Рыба становится больше с возрастом. Насколько предсказуема длина рыбы (см) с возрастом (год)? Являются ли отношения лучше всего подходящими для простой линейной регрессии?
Видео:Математика #1 | Корреляция и регрессияСкачать

Оглавление
- Получить данные, визуализировать и предварительный анализ
- Линейный регрессионный анализ
- Квадратичный и полиномиальный регрессионный анализ высокой степени
- Сегментируйте данные в обучении и тестировании
- Тестовые модели по типу регрессии (линейный, квадратичный, половой)
Видео:Линейная регрессия. Что спросят на собеседовании? ч.1Скачать

Часть 1: извлечение данных, визуализация и предварительный анализ
Во-первых, давайте введем данные и несколько важных модулей:
В наборе данных 77 экземпляров. Ниже приводится глава исходных данных:
Теперь давайте визуализируем график рассеяния. Мы попытаемся предсказать длину от возраста, поэтому оси находятся в своих соответствующих положениях:
Там, кажется, тенденция. По мере того, как рыба становится старше, кажется, что существует связь с длиной. Чтобы получить дальнейшую перспективу, давайте разбить каждую ось на свою собственную одномерную гистограмму распределения.
Y — длина рыбы:
X — Возраст рыбы:
Мы видим, что средняя длина составляет 143,6 см, а средний возраст — 3,6 года. Стандартное отклонение по возрасту пропорционально больше, чем по длине, что предполагает более высокий общий разброс в распределении по возрасту. Это несмотря на то, что распределение длины имеет больший диапазон.
Видео:Линейная регрессия в Python за 13 МИН для чайников [#Машинное Обучения от 16 летнего Школьника]Скачать
![Линейная регрессия в Python за 13 МИН для чайников [#Машинное Обучения от 16 летнего Школьника]](https://i.ytimg.com/vi/y--76SrfRm8/0.jpg)
Часть 2: Простая линейная регрессия
Простая линейная регрессия является одним из кардинальных типов прогностических моделей. Проще говоря, он измеряет отношения между двумя переменными путем подгонки линейного уравнения к данным. Одна переменная считается пояснительной (возраст), а другая — зависимой (длина). Модель регрессии минимизирует расстояние между прямой и каждой точкой данных, чтобы найти оптимальное соответствие.
Ниже мы используем модуль статистики scipy для вычисления ключевых показателей для нашей линии. Ниже выводятся точки пересечения и наклон соответственно.
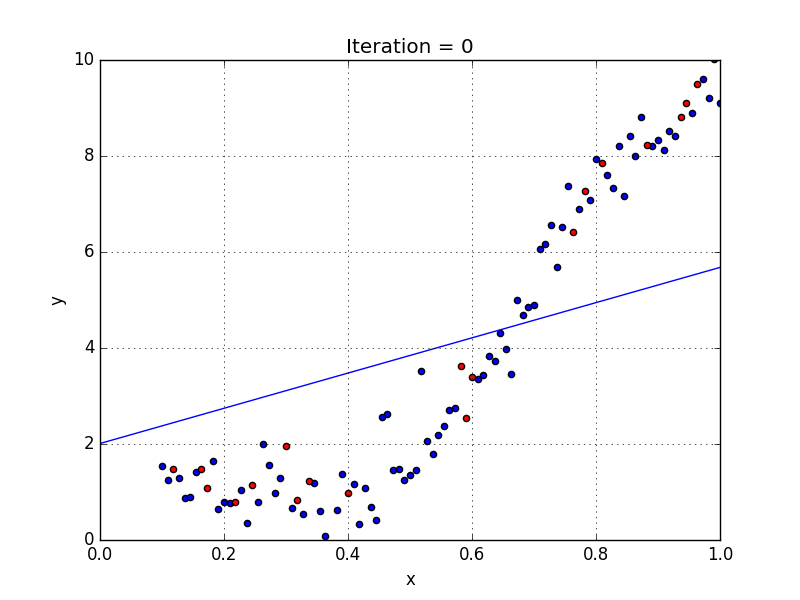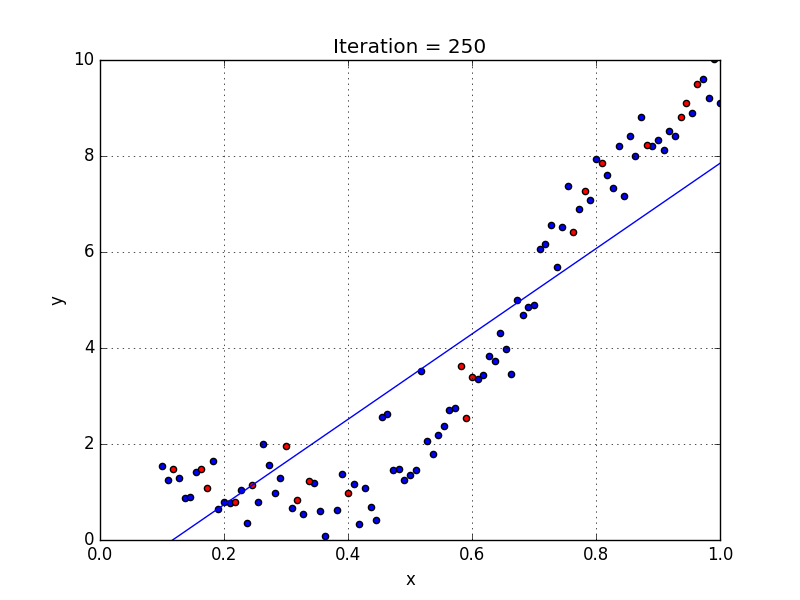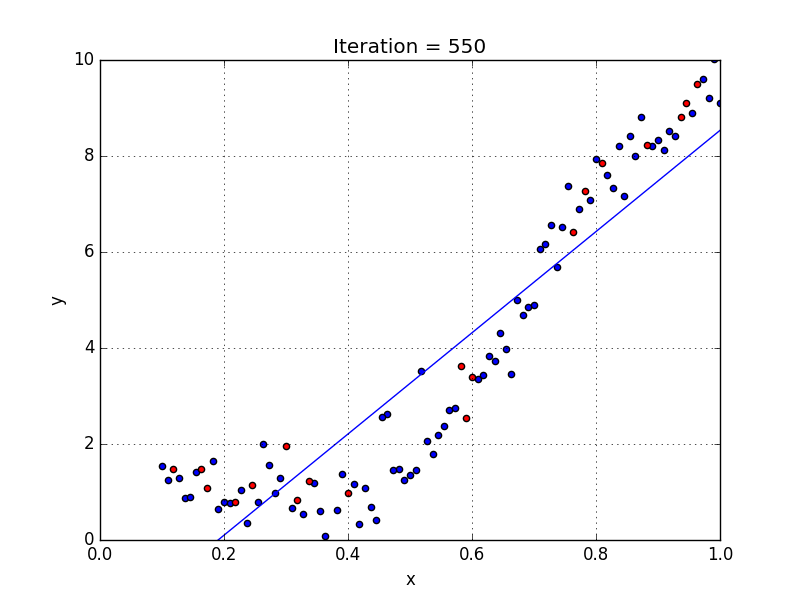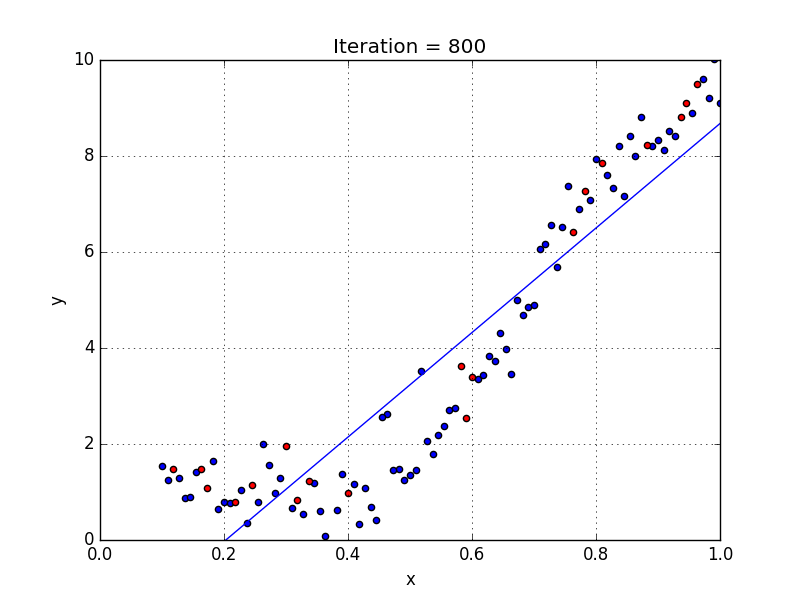
Теперь мы построим эту линию на исходной диаграмме рассеяния, пропустив каждое значение x через линейное уравнение:y = b0 + b1x
Значение rsquared для этой линии регрессии показывает, что возраст объясняет 73% изменения длины. R-квадрат вычисляет, насколько линия регрессии похожа на данные, к которым она привязана. Я написал еще одну статью о rsquared вы можете ссылатьсяВот,
Другими независимыми переменными, которые могут объяснить оставшиеся 27% -ные отклонения по длине, могут быть наличие пищи, качество воды, солнечный свет, генетика рыб и т. Д. Если бы у нас были данные по всем этим признакам, мы могли бы провести многомерную регрессию и получить лучшую модель , Но, увы, мы живем в мире с ограниченными данными.
Интуитивно, наша простая линейная модель не проходит через среднюю точку каждого кластера из y точек. В течение 1, 2, 5 и 6 лет он превышает медиану кластера. Это наиболее вероятно, потому что большая часть выборки имеет возраст 3 и 4, как мы видели ранее. Это сдвигает линию вверх.
Кажется, что оптимальная линия должна была бы изогнуться, чтобы соответствовать данным более точно. Вот где начинается полиномиальная регрессия.
Видео:Метод наименьших квадратов. Линейная аппроксимацияСкачать

Часть 3: Квадратичный и полиномиальный регрессионный анализ высокой степени
Проще говоря, модели полиномиальной регрессии могут изгибаться. Они могут быть построены до n-й степени, чтобы минимизировать квадратичную ошибку и максимизировать rsquared. В зависимости от n-й степени линия наилучшего соответствия может иметь более или менее кривые. Чем выше показатель, тем больше кривых.
Ниже у нас есть некоторый код для создания новой линии и построения графика на нашем точечном графике. Эта линия является квадратичной функцией, потому что она возведена только во вторую степень. Квадратичные линии могут сгибаться только один раз. Как мы видим на графике ниже, новая полиномиальная модель сопоставляет данные с большей точностью.
Значение rsquared составляет 0,80 по сравнению со значением 0,73, которое мы видели в простой линейной модели. Это означает, что 80% длины объясняется их возрастом в этой новой модели.
Теперь мы можем поэкспериментировать с изменением n-го значения нашей модели, чтобы увидеть, сможем ли мы найти более подходящую линию. Тем не менее, мы должны помнить, что переоснащение — это риск, с которым мы столкнемся, чем выше.
Ниже приведен пример полинома, возведенного в6 степень:
Он обслуживает слишком экстремально к выбросам и слишком тесно связан с данными. Значение rsquared для этой модели составляет 0,804, что не намного выше, чем для квадратичной модели.
Для этого набора данных большинство согласится с тем, что квадратичная функция соответствует лучше всего.
Видео:Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать

Часть 4. Сегментируйте данные в обучении и тестировании
Откуда мы знаем, что линия квадратичной полиномиальной регрессии, скорее всего, оптимально подходит для этого набора данных? Вот где приходит концепция тестирования наших данных!
Во-первых, давайте перемешать набор данных.Затем нам нужно разделить его на сегменты обучения и тестирования. Данные обучения используются для создания нашей модели; данные тестирования используются, чтобы увидеть, насколько хорошо модель соответствует. Eстьпрактическое правилоразделить на 70% обучения и 30% тестирования. Поскольку это сравнительно небольшой размер выборки рыбы (n = 78), я решил пойти немного тяжелее на стороне тестирования. Я сделал 50 экземпляров в качестве обучения и последние 28 в качестве тестирования. Это 65/35 раскол.
На тренировочном графике больше баллов по сравнению с тестированием, это связано с нашим расщеплением 65/35:
Видео:Эконометрика Линейная регрессия и корреляцияСкачать

Часть 5. Тестовые модели по типу регрессии
Тест линейной модели:
Теперь мы создадим линейную модель на основе данных обучения:
Линия прекрасно сочетается с тренировочным набором. Квадратное значение 0,75 довольно хорошее:
Теперь давайте посмотрим, как эта строка соответствует данным тестирования, которые мы сохранили:
Модель выглядит прилично. Он не учитывает выбросы в возрасте 6 лет, а также выглядит немного низким по отношению к средней длине каждого возрастного кластера. Эти опасения обоснованы в нижнем квадрате:
Тест квадратичной модели:
Давайте посмотрим, как квадратичная регрессия сравнивается с простой линейной регрессией. Код для этих вычислений очень похож на приведенные выше, просто измените «1» на «2» при определении регрессии в методе numpy.polyfit:
p2= np.poly1d (np.polyfit (trainx, trainy,2)).
Квадратичная регрессия имеет более высокий уровень тренинга. Кроме того, он не так сильно снизился по сравнению с данными тестирования.
Sextic (n6) регрессионный тест:
Наконец, давайте посмотрим, как выполняется полиномиальная регрессия высокой степени:
Эта модель начинается с наивысшей обучающей ценности, но при ее тестировании она резко падает. Это симптомнад-фитинга,
Видео:Парная регрессия: линейная зависимостьСкачать

Вывод:
Квадратичная регрессия лучше всего соответствует данным в этом примере. Однако перетасовка до сегментирования обучения / тестирования может повлиять на эти результаты. В зависимости от того, какие строки окажутся в каком сегменте, результаты rsquared могут немного измениться. Это особенно верно для небольших наборов данных, таких как этот.
Источник исходных данных:Penn State,
Пожалуйста, подпишитесь, хлопните или прокомментируйте, если вы нашли это полезным.
Спасибо за чтение!
Другие статьи от меня, если вы хотите узнать больше:
Видео:Линейная регрессияСкачать

5 видов регрессии и их свойства
Линейная и логистическая регрессии обычно являются первыми видами регрессии, которые изучают в таких областях, как машинное обучение и наука о данных. Оба метода считаются эффективными, так как их легко понять и использовать. Однако, такая простота также имеет несколько недостатков, и во многих случаях лучше выбирать другую регрессионную модель. Существует множество видов регрессии, каждый из которых имеет свои достоинства и недостатки.
Мы познакомимся с 7 наиболее распространенными алгоритмами регрессии и опишем их свойства. Также мы узнаем, в каких ситуация и с какими видами данных лучше использовать тот или иной алгоритм. В конце мы расскажем о некоторых инструментах для построения регрессии и поможем лучше разобраться в регрессионных моделях в целом!
Видео:Множественная регрессия в ExcelСкачать

Линейная регрессия
Регрессия — это метод, используемый для моделирования и анализа отношений между переменными, а также для того, чтобы увидеть, как эти переменные вместе влияют на получение определенного результата. Линейная регрессия относится к такому виду регрессионной модели, который состоит из взаимосвязанных переменных. Начнем с простого. Парная (простая) линейная регрессия — это модель, позволяющая моделировать взаимосвязь между значениями одной входной независимой и одной выходной зависимой переменными с помощью линейной модели, например, прямой.
Более распространенной моделью является множественная линейная регрессия, которая предполагает установление линейной зависимости между множеством входных независимых и одной выходной зависимой переменных. Такая модель остается линейной по той причине, что выход является линейной комбинацией входных переменных. Мы можем построить модель множественной линейной регрессии следующим образом:
Y = a_1*X_1 + a_2*X_2 + a_3*X_3 ……. a_n*X_n + b
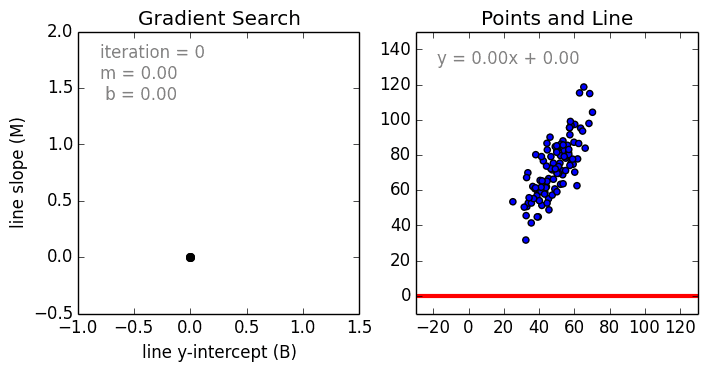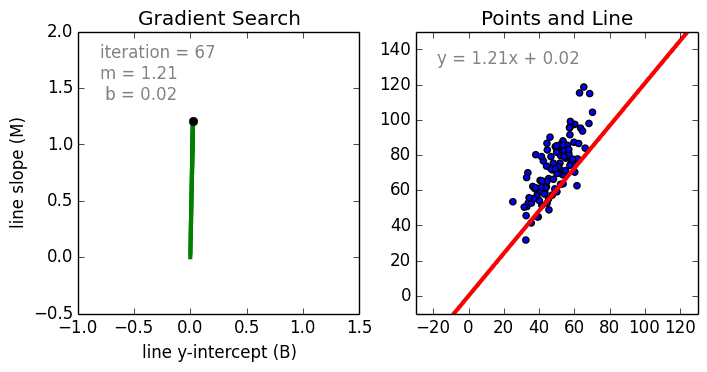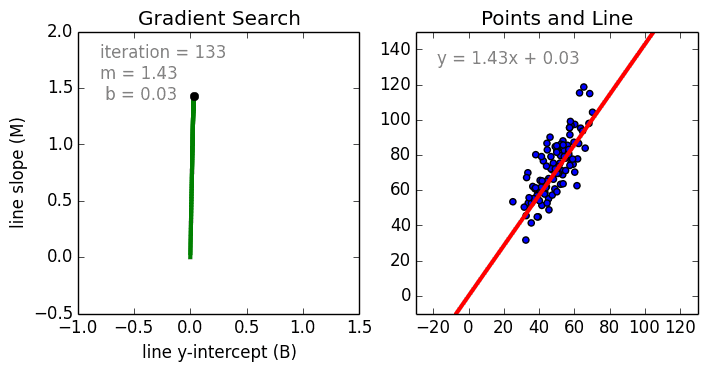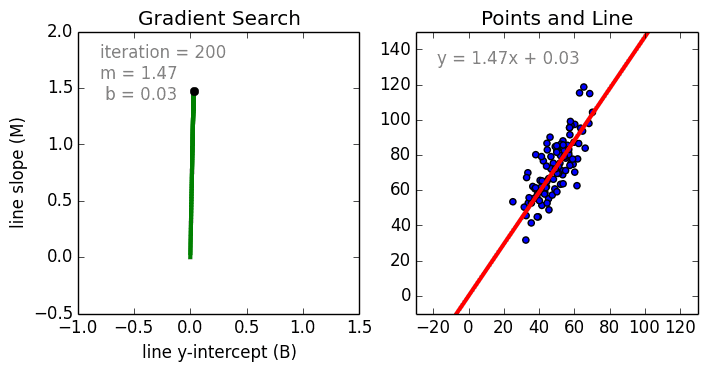
Где a_n — это коэффициенты, X_n — переменные и b — смещение . Как видим, данная функция не содержит нелинейных коэффициентов и, таким образом, подходит только для моделирования линейных сепарабельных данных. Все очень просто: мы взвешиваем значение каждой переменной X_n с помощью весового коэффициента a_n. Данные весовые коэффициенты a_n, а также смещение b вычисляются с применением стохастического градиентного спуска. Посмотрите на график ниже в качестве иллюстрации!
Несколько важных пунктов о линейной регрессии:
- Она легко моделируется и является особенно полезной при создании не очень сложной зависимости, а также при небольшом количестве данных.
- Обозначения интуитивно-понятны.
- Чувствительна к выбросам.
Видео:РЕАЛИЗАЦИЯ ЛИНЕЙНОЙ РЕГРЕССИИ | Линейная регрессия | LinearRegression | МАШИННОЕ ОБУЧЕНИЕСкачать
Полиномиальная регрессия
Для создания такой модели, которая подойдет для нелинейно разделяемых данных, можно использовать полиномиальную регрессию. В данном методе проводится кривая линия, зависимая от точек плоскости. В полиномиальной регрессии степень некоторых независимых переменных превышает 1. Например, получится что-то подобное:
Y = a_1*X_1 + (a_2)²*X_2 + (a_3)⁴*X_3 ……. a_n*X_n + b
У некоторых переменных есть степень, у других — нет. Также можно выбрать определенную степень для каждой переменной, но для этого необходимы определенные знания о том, как входные данные связаны с выходными. Сравните линейную и полиномиальную регрессии ниже.
Несколько важных пунктов о полиномиальной регрессии:
- Моделирует нелинейно разделенные данные (чего не может линейная регрессия). Она более гибкая и может моделировать сложные взаимосвязи.
- Полный контроль над моделированием переменных объекта (выбор степени).
- Необходимо внимательно создавать модель. Необходимо обладать некоторыми знаниями о данных, для выбора наиболее подходящей степени.
- При неправильном выборе степени, данная модель может быть перенасыщена.
Видео:Полиномиальная регрессияСкачать

Гребневая (ридж) регрессия
В случае высокой коллинеарности переменных стандартная линейная и полиномиальная регрессии становятся неэффективными. Коллинеарность — это отношение независимых переменных, близкое к линейному. Наличие высокой коллинеарности можно определить несколькими путями:
- Коэффициент регрессии не важен, несмотря на то, что, теоретически, переменная должна иметь высокую корреляцию с Y.
- При добавлении или удалении переменной из матрицы X, коэффициент регрессии сильно изменяется.
- Переменные матрицы X имеют высокие попарные корреляции (посмотрите корреляционную матрицу).
Сначала можно посмотреть на функцию оптимизации стандартной линейной регрессии для лучшего понимания того, как может помочь гребневая регрессия:
Где X — это матрица переменных, w — веса, y — достоверные данные. Гребневая регрессия — это корректирующая мера для снижения коллинеарности среди предикторных переменных в регрессионной модели. Коллинеарность — это явление, в котором одна переменная во множественной регрессионной модели может быть предсказано линейно, исходя из остальных свойств со значительной степенью точности. Таким образом, из-за высокой корреляции переменных, конечная регрессионная модель сведена к минимальным пределам приближенного значения, то есть она обладает высокой дисперсией.
Гребневая регрессия добавляет небольшой фактор квадратичного смещения для уменьшения дисперсии:
min || Xw — y ||² + z|| w ||²
Такой фактор смещения выводит коэффициенты переменных из строгих ограничений, вводя в модель небольшое смещение, но при этом значительно снижая дисперсию.
Несколько важных пунктов о гребневой регрессии:
- Допущения данной регрессии такие же, как и в методе наименьших квадратов, кроме того факта, что нормальное распределение в гребневой регрессии не предполагается.
- Это уменьшает значение коэффициентов, оставляя их ненулевыми, что предполагает отсутствие отбора признаков.
Видео:Эконометрика. Линейная парная регрессияСкачать

Регрессия по методу «лассо»
В регрессии лассо, как и в гребневой, мы добавляем условие смещения в функцию оптимизации для того, чтобы уменьшить коллинеарность и, следовательно, дисперсию модели. Но вместо квадратичного смещения, мы используем смещение абсолютного значения:
min || Xw — y ||² + z|| w ||
Существует несколько различий между гребневой регрессией и лассо, которые восстанавливают различия в свойствах регуляризаций L2 и L1:
- Встроенный отбор признаков — считается полезным свойством, которое есть в норме L1, но отсутствует в норме L2. Отбор признаков является результатом нормы L1, которая производит разреженные коэффициенты. Например, предположим, что модель имеет 100 коэффициентов, но лишь 10 из них имеют коэффициенты отличные от нуля. Соответственно, «остальные 90 предикторов являются бесполезными в прогнозировании искомого значения». Норма L2 производит неразряженные коэффициенты и не может производить отбор признаков. Таким образом, можно сказать, что регрессия лассо производит «выбор параметров», так как не выбранные переменные будут иметь общий вес, равный 0.
- Разряженность означает, что незначительное количество входных данных в матрице (или векторе) имеют значение, отличное от нуля. Норма L1 производит большое количество коэффициентов с нулевым значением или очень малые значения с некоторыми большими коэффициентами. Это связано с предыдущим пунктом, в котором указано, что лассо исполняет выбор свойств.
- Вычислительная эффективность: норма L1 не имеет аналитического решения в отличие от нормы L2. Это позволяет эффективно вычислять решения нормы L2. Однако, решения нормы L1 не обладают свойствами разряженности, что позволяет использовать их с разряженными алгоритмами для более эффективных вычислений.
Видео:#3. Линейная модель. Понятие переобучения | Машинное обучениеСкачать

Регрессия «эластичная сеть»
Эластичная сеть — это гибрид методов регрессии лассо и гребневой регрессии. Она использует как L1, так и L2 регуляризации, учитывая эффективность обоих методов.
min || Xw — y ||² + z_1|| w || + z_2|| w ||²
Практическим преимуществом использования регрессии лассо и гребневой регрессии является то, что это позволяет эластичной сети наследовать некоторую стабильность гребневой регрессии при вращении.
Несколько важных пунктов о регрессии эластичной сети:
- Она создает условия для группового эффекта при высокой корреляции переменных, а не обнуляет некоторые из них, как метод лассо.
- Нет ограничений по количеству выбранных переменных.
Видео:Лекция 2.1: Линейная регрессия.Скачать

Вывод
Вот и все! 5 распространенных видов регрессии и их свойства. Все данные методы регуляризации регрессии (лассо, гребневая и эластичной сети) хорошо функционирует при высокой размерности и мультиколлинеарности среди переменных в наборе данных.
📹 Видео
Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать

Множественная регрессияСкачать

Линейная регрессияСкачать

Лекция 8. Линейная регрессияСкачать