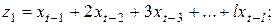Уравнение регрессии по первым разностям

Видео:Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать

Уравнение регрессии по первым разностям

Видео:Эконометрика Линейная регрессия и корреляцияСкачать

Первая разность

Фактически исходный ряд цен заменяется относительными величинами изменения уровня ряда в единицу времени (или темпами прироста) их первых разностей, что, как известно, в принципе является одним из способов устранения тренда. [c.371]

Выработано правило выбора степени полинома модели развития, основанное на определении величин конечных разностей уровней динамических рядов. Согласно этому правилу полином первой степени (прямая) применяется как модель такого ряда динамики, у которого первые разности (абсолютные приросты) примерно одинаковы полиномы второй степени — для отражения ряда динамики с примерно одинаковыми вторыми разностями (ускорениями) полиномы третьей степени с примерно одинаковыми третьими разностями и т.д. [c.80]

При переходе от уровней к их разностям исключается влияние общей тенденции на колеблемость. При изменении уровней по прямой следует коррелировать первые разности, при изменении по пара- [c.87]

Поэтому, а также в силу того, что вторая разность является первой разностью двух соседних первых разностей, мы получим, заменяя одну из первых разностей для колла разностью для пута и наоборот, еще два возможных представления оценки плотности вероятности, а именно, для всех / е / [c.21]

Метод последовательных разностей заключается в следующем если ряд содержит линейный тренд, тогда исходные данные заменяются первыми разностями [c.139]

Построить линейную модель спроса, используя первые разности уровней исходных динамических рядов. [c.144]

Так как ряды динамики имеют общую тенденцию к росту, то для построения регрессионной модели спроса на товар А в зависимости от дохода необходимо устранить тенденцию. С этой целью модель может строиться по первым разностям, т.е. Лу = f (Лх), если ряды динамики характеризуются линейной тенденцией. [c.145]

Уравнение регрессии по первым разностям уровней временных рядов [c.171]

Определите параметры уравнения регрессии по первым разностям и дайте их интерпретацию. В качестве зависимой переменной используйте показатель дивидендов по обыкновенным акциям. [c.172]

В чем состоит причина построения уравнения регрессии по первым разностям, а не по исходным уровням рядов [c.172]

Постройте уравнение линейной регрессии, используя метод первых разностей. [c.173]

Охарактеризуйте тесноту связи между рядами по их уровням, по первым разностям. Сделайте выводы. [c.173]

Yt =2-0,5 б) по первым разностям уровней [c.173]

Ряд По уровням ряда По первым разностям уровней рада По вторым разностям уровней ряда [c.173]

Определите коэффициенты корреляции по уровням временных рядов, по первым разностям временных рядов и по вторым разностям временных рядов. Охарактеризуйте тесноту связи между временными рядами рентабельности продукции и численности занятых ручным трудом. Обоснуйте ваш выбор одной из мер тесноты связи. [c.174]

Определите коэффициент корреляции между временными рядами, используя непосредственно исходные уровни, первые разности для электровооруженности и вторые разности для производительности труда, отклонения от основной тенденции. [c.174]

Это привело к идее измерения корреляции не самих уровней х, иу а первых разностей Дх, = х, — , ,, 6у, — у, — у. (при линейных трендах). В общем случае было признано необходимым коррелировать отклонения от трендов (за вычетом циклической компоненты) Еу —у, — %, Ех = х, — %, (у,,% — тренды временных рядов). [c.19]

Если временной ряд содержит ярко выраженную линейную тенденцию, ее можно устранить путем замены исходных уровней ряда цепными абсолютными приростами (первыми разностями). [c.268]

Коэффициент Ь — константа, которая не зависит от времени. При наличии сильной линейной тенденции остатки е, достаточно малы и в соответствии с предпосылками МНК носят случайный характер. Поэтому первые разности уровней ряда Д, не зависят от переменной времени, их можно использовать для дальнейшего анализа. [c.269]

Как показывает это соотношение, первые разности Д, непосредственно зависят от фактора времени / и, следовательно, содержат тенденцию. [c.269]

Пример 6.2. Изучение зависимости расходов на конечное потребление от совокупного дохода по первым разностям. [c.269]

Обратимся вновь к данным о расходах на конечное потребление у, и совокупном доходе х, (табл. 6.1). Проанализируем зависимость между этими рядами, используя для этого первые разности (табл. 6.4). [c.269]

Первые разности временных рядов расходов на конечное потребление и совокупного дохода [c.270]

Построение уравнения регрессии зависимости расходов на конечное потребление от совокупного дохода по первыми разностям привело к следующим результатам [c.270]

Проверим гипотезу о наличии автокорреляции в остатках для модели зависимости расходов на конечное потребление от совокупного дохода, построенной по первым разностям исходных показателей, используя данные примера 6.2. [c.277]

В чем сущность метода последовательных разностей Какова интерпретация параметров уравнения регрессии по первым разностям уровней рядов [c.289]

Модель регрессии (7.69) называют механизмом корректировки посредством ошибок. Если коэффициент Ьг статистически значим, то его величина характеризует долю неравновесного состояния временного ряда у которая корректируется в каждом следующем периоде. Поскольку Ау, в модели (7.69) есть первые разности исходных уровней ряда, можно сказать, что коэффициент Ь2 характеризует скорость корректировки ряда у, во времени по направлению к достижению равновесного состояния. [c.335]

Рис.2.3.2. Автокорреляционная функция первой разности

Автокорреляционные функции первых разностей главных компонент временной струк- [c.93]

Этот прогноз делался на основе первых разностей Asn = sn- sn. с ис- [c.84]

Прозрачность» рынка 313 «Пункт» обслуживания 138, 295 Паутинообразная модель 260 Первая разность 299 Первичная информация 134, 317 Первичная экономическая информация [c.481]

В этом преобразовании при автокорреляции первого порядка используется и первое наблюдение даже тогда, когда первая разность с предыдущим наблюдением для него недоступна. Это делается путем введения для него веса [c.393]

Это происходит по двум причинам. Во-первых, капитальные вложения, прежде чем увеличить основные фонды, должны трансформироваться во вводы, при этом их колебания могут быть смягчены изменениями заделов незавершенного строительства, являющихся своеобразным амортизатором. Чем выше норма незавершенного строительства, тем в большей мере оно может выполнять эти амортизирующие функции. Во-вторых, колебания приростов капитальных вложений и вводов отражают лишь изменения разностей второго порядка по отношению к увеличивающейся массе основных фондов. Действительно, величинам капитальных вложений и вводов корреспондируют приросты основных фондов (первые разности), а изменения темпов прироста самих капитальных вложений и вводов корреспондируют приростам приростов основных фондов (их вторым разностям). Изменение же темпов роста конечного общественного продукта в каждый, относительно ограниченный отрезок времени влияет лишь на темпы прироста капитальных вложений и вводов. Это главная причина того, что импульс, идущий от колебаний производства, сказывается на динамике основных фондов в ослабленном виде. [c.34]

Фактически же расчетная задача сводится к оценке средней эластичности в течение более или менее длительного периода времени. С использованием хорошо зарекомендовавшего себя метода коррелирования первых разностей логарифмов [10] по заданным переменным (без исключения временного тренда) был получен коэффициент эластичности по данным овошного рынка. [c.329]

Существует ряд подходов преодоления сильной межфакторной корреляции. Самый простой путь устранения мультиколли-неарности состоит в исключении из модели одного или нескольких факторов. Другой подход связан с преобразованием факторов, при котором уменьшается корреляция между ними. Например, при построении модели на основе рядов динамики переходят от первоначальных данных к первым разностям уровней At = у, — у, , чтобы исключить влияние тенденции, или используются такие методы, которые сводят к нулю межфакторную корреляцию, т. е. переходят от исходных переменных к их линейным комбинациям, не коррелированных друг с другом (метод главных компонент). [c.97]

Результаты проверки временных рядов первых разностей на автокорреляцию приведены в последней строке табл. 6.4. Поскольку полученные ряды не содержат автокорреляции, будем использовать их вместо исходных данных для измерения зависимости между расходами на конечное потребление и совокупным доходом. Коэффициент корреляции этих рядов по первым разностям составляет rAjKdt(y= 0,717. Это подтверждает вывод о наличии тесной прямой связи между расходами на конечное потребление и совокупным доходом, приведенный в примере 6.1. [c.270]

Обобщенный метод наименьших квадратов аналогичен методу последовательных разностей. Однако мы вычитаем из у, (или xt) не все значение предыдущего уровня > , , (илил , ), а некоторую его долю — гЕ у, или ге( , ,. Если rz = 1, данный метод есть просто метод первых разностей, так как [c.281]

Поэтому в случае, если значение критерия Дарбина — Уотсо-на близко к нулю, применение метода первых разностей вполне обоснованно. Если гЕ = — 1, т. е. в остатках наблюдается полная отрицательная автокорреляция, то изложенный выше метод модифицируется следующим образом [c.281]

Видео:Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать

Корреляция и регрессия по первым разностям

Для оценки тесноты связи по первым разностям используем формулу:

.

где , — первые разности

Построим вспомогательную таблицу 5.10.

Таблица 5.10 – Расчет коэффициента корреляции

t	y	x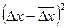
325,69	15,69	—	—	—	—	—
340,79	16,69	15,10	1,00	15,10	1,52	0,04
349,39	17,69	8,60	1,00	8,60	59,81	0,04
373,59	19,09	24,20	1,40	33,88	61,88	0,04
389,79	20,79	16,20	1,70	27,54	0,02	0,24
399,09	21,69	9,30	0,90	8,37	49,47	0,10
421,49	23,09	22,40	1,40	31,36	36,80	0,04
441,39	24,09	19,90	1,00	19,90	12,72	0,04
458,29	25,19	16,90	1,10	18,59	0,32	0,01
472,33	26,58	14,04	1,39	19,49	5,28	0,03
489,02	27,81	16,70	1,23	20,48	0,13	0,00
Итого	4460,86	238,39	163,33	12,12	203,32	227,95	0,59
В среднем	405,53	21,67	16,33	1,21	20,33	22,80	0,06

Подставляя в формулу наши данные, получим:

.

Следовательно, можно сделать вывод о наличии прямой связи средней силы скорости ряда энерговооруженности 1 рабочего и скорости ряда выпуска продукции.

Для оценки параметров уравнения регрессии по первым разностям воспользуемся встроенной функцией MS Excel. Результаты оценивания представлены в приложении В.

Уравнение регрессии примет вид:

.

Оно показывает, что рост скорости энерговооруженности 1 рабочего на 1 кВт/ч, способствует росту скорости для ряда выпуска продукции на 13,6 тыс. тонн.

Прогнозирование осуществим по формуле:

.

Прогноз выпуска продукции на 2006 год, при ожидаемом увеличении энерговооруженности на 1 кВт/ч относительно 11 года, составит:

тыс. тонн.

Корреляция и регрессия по отклонениям от тренда

Коэффициент корреляции по отклонениям от тренда имеет вид:

,

где , — отклонения фактических значений ряда от тренда, т.е. , .

В качестве аппроксимирующей модели примем линейный тренд. Оценим параметры трендов с помощью встроенной функции MS Excel. Результаты представлены на рисунках 5.4 и 5.5.

Рисунок 5.4 – Динамика выпуска продукции

Рисунок 5.5 – Динамика энерговооруженности рабочих

Таблица 5.11 – Расчет коэффициента корреляции по остаточным величинам

t	y	x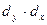
325,69	15,69	322,04	15,54	3,65	0,15	0,55	13,33	0,02
340,79	16,69	338,74	16,77	2,05	-0,08	-0,16	4,22	0,01
349,39	17,69	355,43	17,99	-6,04	-0,30	1,83	36,53	0,09
373,59	19,09	372,13	19,22	1,46	-0,13	-0,19	2,12	0,02
389,79	20,79	388,83	20,45	0,96	0,34	0,33	0,92	0,12
399,09	21,69	405,53	21,67	-6,44	0,02	-0,11	41,45	0,00
421,49	23,09	422,23	22,90	-0,74	0,19	-0,14	0,54	0,04
441,39	24,09	438,92	24,13	2,47	-0,04	-0,09	6,08	0,00
458,29	25,19	455,62	25,35	2,67	-0,16	-0,43	7,12	0,03
472,33	26,58	472,32	26,58	0,01	0,00	0,00	0,00	0,00
489,02	27,81	489,02	27,81	0,01	0,00	0,00	0,00	0,00
—	—	505,72	29,03	—	—	—	—	—
Итого	4460,86	238,39	4460,81	238,39	0,05	-0,01	1,59	112,32	0,32
В среднем	405,53	21,67	405,53	21,67	0,00	0,00	0,14	10,21	0,03

Тогда коэффициент корреляции рядов x и y по отклонениям от тренда составит:

.

Следовательно, связь между случайными отклонениями по ряду 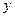и ряду прямая слабая.

Регрессия по отклонениям от трендаимеет вид . Оценим параметры модели с помощью встроенной функции MS Excel. Результаты оценивания представлены в приложении Г.

Уравнение регрессии примет вид:

.

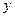
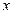
Коэффициент регрессии означает, что случайные отклонения по ряду в среднем в 18,55 раз выше случайных колебаний по ряду .

Прогнозная модель по отклонениям от тренда имеет вид:

,

где — прогнозное значение результативного признака;

— прогноз по тренду результативного признака;

— прогнозное значение факторного признака;

— прогноз по тренду факторного признака.

Тогда, подставив соответствующие значения в модель, получим прогноз выпуска продукции на 12 год, при ожидаемой энерговооруженности =28,81 кВт/ч:

тыс. тонн.

Видео:Парная регрессия: линейная зависимостьСкачать

Уравнение регрессии по первым разностям

Ежегодные абсолютные приросты (первые разности) определяются по формулам , .

Если ряды динамики характеризуются линейной тенденцией, то модель можно построить в виде . Для подтверждения линейной тенденции найдем по каждому ряду коэффициенты автокорреляции первого порядка.

Эти коэффициенты близки к единице, поэтому целесообразно моделировать взаимосвязь рядов по первым разностям. Если бы при невысоких значениях , достаточно высокими окажутся коэффициенты , есть смысл моделировать по вторым разностям .

Строим уравнение .

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,751809412
R-квадрат	0,565217391
Нормированный R-квадрат	0,420289855
Стандартная ошибка	0,868114732
Наблюдения
Дисперсионный анализ
df	SS	MS	F	Значимость F
Регрессия	2,93913	2,93913	3,9	0,142772
Остаток	2,26087	0,753623
Итого	5,2
Коэффициенты	Стандартная ошибка	t-статистика	P-Значение
a	2,565217391	1,101068	2,329754	0,102171
b	0,565217391	0,286209	1,974842	0,142772
ВЫВОД ОСТАТКА
Наблюдение	Предсказанное Y	Остатки
4,260869565	0,73913	0,546314
3,695652174	0,304348	0,092628	0,189036
4,826086957	0,173913	0,030246	0,017013
5,956521739	0,043478	0,00189	0,017013
4,260869565	-1,26087	1,589792	1,701323
2,26087	1,924386

Ø Уравнение достоверно на 56,52%.

Ø Статистика критерия Фишера – 3,9; значимость F – 0,14, что превышает допустимый уровень значимости 0,05. Уравнение в целом признаем незначимым.

Ø Из коэффициентов регрессии ни один нельзя признать значимым. Уровень ошибки везде превышает 0,05.

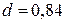
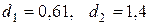
Ø Статистика Дарбина-Уотсона . Критические значения критерия . Поскольку выполняется неравенство , гипотеза о независимости остатков отклоняется, и модель признается неадекватной по данному критерию.

Вывод: таким образом, на данном этапе наиболее пригодным для прогнозирования считаем уравнение с включенным фактором времени.

Лабораторная работа №9

Моделирование временных рядов

С распределенным лагом

Рассмотрим модель с распределенным лагом в ее общем виде в предположении, что максимальная величина лага конечна:

.

Данная модель говорит о том, что если в некоторый момент времени t происходит изменение независимой переменной x, то это изменение будет влиять на значения переменной y в течение l следующих моментов времени.

Коэффициент регрессии при перемеренной характеризует среднее абсолютное изменение при изменении на 1 единицу своего измерения в некоторый фиксированный момент времени , без учета воздействия лаговых значений фактора . Этот коэффициент называют краткосрочным мультипликатором.

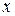
В момент совокупное воздействие факторной переменной на результат составит условных единиц, в момент это воздействие можно охарактеризовать суммой и т. д. Полученные таким образом суммы называют промежуточным мультипликаторами.

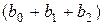
С учетом конечной величины лага можно сказать, что изменение переменной в момент на 1 у.е. приведет к общему изменению результата через моментов времени на абсолютных единиц.

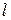
Введем следующее обозначение:

Величину называют долгосрочным мультипликатором, который показывает абсолютное изменение в долгосрочном периоде результата под влиянием изменения на 1 ед. фактора .

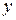
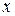
Предположим,

.

Назовем полученные величины относительными коэффициентами модели с распределенным лагом. Если все коэффициенты имеют одинаковые знаки, то выполняются условия и . Каждый из коэффициентов измеряет долю от общего изменения результативного признака в момент времени .

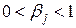
Зная величины , можно определить еще две важные характеристики: величину среднего и медианного лагов.

Средний лаг вычисляется по формуле

и представляет собой средний период, в течение которого будет происходить изменение результата под воздействием изменения фактора в момент времени t. Небольшая величина среднего лага свидетельствует об относительно быстром реагировании результата на изменение фактора, тогда как высокое его значение говорит о том, что воздействие фактора на результат будет сказываться в течение длительного периода времени.

Медианный лаг – это величина лага, для которого . Это период времени, в течение которого с момента времени t будет реализована половина общего воздействия фактора на результат.

Лаги, структуру которых можно описать с помощью полиномов, называют лагами Алмон.

Формально модель зависимости коэффициентов от величины лага j в форме полинома можно записать так:

.

Тогда каждый из коэффициентов модели можно выразить следующим образом:

(*)

Подставив данные соотношения в модель, и перегруппировав слагаемые, получим

Введем новые обозначения

.

Тогда модель с распределенным лагом будет выглядеть следующим образом:

.

Процедура применения метода Алмон для расчета параметров модели с распределенным лагом выполняется следующим образом:

1. Определяется максимальная величина лага l.

2. Определяется степень полинома k, описывающего структуру лага.

3. Рассчитываются значения переменных .

4. Определяются параметры уравнения линейной регрессии по данным значениям и .

5. С помощью соотношений (*) рассчитываются параметры исходной модели с распределенным лагом .

В таблице представлены данные по региону о месячном доходе на душу населения (x) и денежных расходах населения (y) по месяцам за 2 года.

I. Построить модель с распределенным лагом используя лаги от одного до трех месяцев

При этом необходимо:

1. применить обычный МНК;

2. применить метод Алмон, исходя из предположения, что лаг имеет линейную структуру ;

3. Рассчитать средний и медианный лаги.

II. Построить модель с распределенным лагом используя лаги от одного до четырех месяцев

.

При этом необходимо:

1. применить обычный МНК;

2. применить метод Алмон, исходя из предположения, что структура лага описывается полиномом второй степени , где

3. Рассчитать средний и медианный лаги.

I. Выполняем расчет для регрессии через Анализ данных/Регрессия. Для этого строим вспомогательную таблицу

То есть модель имеет вид

.

Удовлетворительным результат назвать нельзя, поскольку

· вычисленные коэффициенты не являются статистически значимыми (вероятность ошибки их расчета значительно превышают допустимый уровень в 0,05);

· коэффициенты имеют разные знаки, что противоречит здравому смыслу: влияние признака x в разные периоды не может быть разнонаправленным.

2) Применяем метод Алмон для расчета параметров модели

.

а) Структура лага линейная, т.е.

Необходимо преобразовать исходные данные в новые переменные . Это преобразование выглядит следующим образом:

.

Строим регрессию

По найденным коэффициентам находим параметры , а именно

Получили модель с распределенным лагом

.

Эта регрессия лишена недостатков предыдущей:

· вычисленные коэффициенты являются статистически значимыми (вероятность ошибки их расчета почти не превышают допустимый уровень в 0,05);

· коэффициенты имеют одинаковые знаки.

Сравним исходные данные и результаты регрессии:

Последнее изменение этой страницы: 2016-07-23; просмотров: 451

🎦 Видео

Множественная регрессия в ExcelСкачать

Математика #1 | Корреляция и регрессияСкачать

Эконометрика. Линейная парная регрессияСкачать

Множественная регрессияСкачать

Уравнение регрессииСкачать

Линейная регрессияСкачать

Что такое линейная регрессия? Душкин объяснитСкачать

Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать

Множественная линейная регрессия, часть 1Скачать

Линейная регрессия в Python за 13 МИН для чайников [#Машинное Обучения от 16 летнего Школьника]Скачать

Линейная регрессия. Что спросят на собеседовании? ч.1Скачать

Что такое линейный и логарифмический переменный резистор.Чем они отличаются и где применяются.Скачать

Уравнение парной линейной регрессии с помощью Анализа ДанныхСкачать

Эконометрика. Множественная регрессия и корреляция.Скачать

Как вычислить линейный коэффициент корреляции в MS Excel и построить уравнение регрессии?Скачать

Критерий Стьюдента и Фишера в Excel, проверка уравнения множественной регрессии в ExcelСкачать