Вместе с этим калькулятором также используют следующие:
Уравнение множественной регрессии
- Виды нелинейной регрессии
- нелинейная регрессия. Нелинейная регрессия. Нелинейная регрессия. Примеры нелинейной регрессии. Методы преобразования полиноминального уравнения регрессии. Преобразование экспоненциальной функции. Коэффициенты эластичности для нелинейных уравнений регрессии
- Нелинейные регрессии
- Линеаризация
- Уравнение параболической регрессии
- 🔍 Видео
Видео:Эконометрика. Нелинейная регрессия: парабола.Скачать

Виды нелинейной регрессии
| Вид | Класс нелинейных моделей |
| Нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам |
| Нелинейные по оцениваемым параметрам |
Здесь ε — случайная ошибка (отклонение, возмущение), отражающая влияние всех неучтенных факторов.
Уравнению регрессии первого порядка — это уравнение парной линейной регрессии.
Уравнение регрессии второго порядка это полиномальное уравнение регрессии второго порядка: y = a + bx + cx 2 .
Уравнение регрессии третьего порядка соответственно полиномальное уравнение регрессии третьего порядка: y = a + bx + cx 2 + dx 3 .
Чтобы привести нелинейные зависимости к линейной используют методы линеаризации (см. метод выравнивания):
- Замена переменных.
- Логарифмирование обеих частей уравнения.
- Комбинированный.
| y = f(x) | Преобразование | Метод линеаризации |
| y = b x a | Y = ln(y); X = ln(x) | Логарифмирование |
| y = b e ax | Y = ln(y); X = x | Комбинированный |
| y = 1/(ax+b) | Y = 1/y; X = x | Замена переменных |
| y = x/(ax+b) | Y = x/y; X = x | Замена переменных. Пример |
| y = aln(x)+b | Y = y; X = ln(x) | Комбинированный |
| y = a + bx + cx 2 | x1 = x; x2 = x 2 | Замена переменных |
| y = a + bx + cx 2 + dx 3 | x1 = x; x2 = x 2 ; x3 = x 3 | Замена переменных |
| y = a + b/x | x1 = 1/x | Замена переменных |
| y = a + sqrt(x)b | x1 = sqrt(x) | Замена переменных |
Пример . По данным, взятым из соответствующей таблицы, выполнить следующие действия:
- Построить поле корреляции и сформулировать гипотезу о форме связи.
- Рассчитать параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессии.
- Оценить тесноту связи с помощью показателей корреляции и детерминации.
- Дать с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
- Оценить с помощью средней ошибки аппроксимации качество уравнений.
- Оценить с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования. По значениям характеристик, рассчитанных в пп. 4, 5 и данном пункте, выбрать лучшее уравнение регрессии и дать его обоснование.
- Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 15% от его среднего уровня. Определить доверительный интервал прогноза для уровня значимости α=0,05 .
- Оценить полученные результаты, выводы оформить в аналитической записке.
| Год | Фактическое конечное потребление домашних хозяйств (в текущих ценах), млрд. руб. (1995 г. — трлн. руб.), y | Среднедушевые денежные доходы населения (в месяц), руб. (1995 г. — тыс. руб.), х |
| 1995 | 872 | 515,9 |
| 2000 | 3813 | 2281,1 |
| 2001 | 5014 | 3062 |
| 2002 | 6400 | 3947,2 |
| 2003 | 7708 | 5170,4 |
| 2004 | 9848 | 6410,3 |
| 2005 | 12455 | 8111,9 |
| 2006 | 15284 | 10196 |
| 2007 | 18928 | 12602,7 |
| 2008 | 23695 | 14940,6 |
| 2009 | 25151 | 16856,9 |
Решение. В калькуляторе последовательно выбираем виды нелинейной регрессии. Получим таблицу следующего вида.
Экспоненциальное уравнение регрессии имеет вид y = a e bx
После линеаризации получим: ln(y) = ln(a) + bx
Получаем эмпирические коэффициенты регрессии: b = 0.000162, a = 7.8132
Уравнение регрессии: y = e 7.81321500 e 0.000162x = 2473.06858e 0.000162x
Степенное уравнение регрессии имеет вид y = a x b
После линеаризации получим: ln(y) = ln(a) + b ln(x)
Эмпирические коэффициенты регрессии: b = 0.9626, a = 0.7714
Уравнение регрессии: y = e 0.77143204 x 0.9626 = 2.16286x 0.9626
Гиперболическое уравнение регрессии имеет вид y = b/x + a + ε
После линеаризации получим: y=bx + a
Эмпирические коэффициенты регрессии: b = 21089190.1984, a = 4585.5706
Эмпирическое уравнение регрессии: y = 21089190.1984 / x + 4585.5706
Логарифмическое уравнение регрессии имеет вид y = b ln(x) + a + ε
Эмпирические коэффициенты регрессии: b = 7142.4505, a = -49694.9535
Уравнение регрессии: y = 7142.4505 ln(x) — 49694.9535
Видео:Метод наименьших квадратов. Линейная аппроксимацияСкачать

нелинейная регрессия. Нелинейная регрессия. Нелинейная регрессия. Примеры нелинейной регрессии. Методы преобразования полиноминального уравнения регрессии. Преобразование экспоненциальной функции. Коэффициенты эластичности для нелинейных уравнений регрессии
| Название | Нелинейная регрессия. Примеры нелинейной регрессии. Методы преобразования полиноминального уравнения регрессии. Преобразование экспоненциальной функции. Коэффициенты эластичности для нелинейных уравнений регрессии |
| Анкор | нелинейная регрессия |
| Дата | 16.11.2020 |
| Размер | 1.57 Mb. |
| Формат файла |  |
| Имя файла | Нелинейная регрессия.pptx |
| Тип | Документы #150878 |
| Подборка по базе: Методические указания, практические материалы и примеры решения , Логоритмика Задание 2 Примеры игр и упражнений Байдакова Л.С. От, Задание 2 Приведите примеры динамичческих стереотипов по три на , Как решать примеры на обратную матрицу.docx, Основы ГО и ЧС, разбор задач, примеры, часть 1.docx, Приведите примеры кибератак нацеленных на физический уровень.do, моделирование, структура и примеры.docx, сборник программ примеры.docx, Базы данных. Примеры баз данных экономического назначения.doc (1, Коучинг примеры. Аружан Казыхан. русс.яз.docx Видео:Решение систем уравнений второй степени. Алгебра, 9 классСкачать  Нелинейные регрессииполиномы разных степеней у =а + bх +сх +dx3+ ε, степенная y = axb ε показательная у = аbх ε В параболе второй степени у= а0 + а1 х + а2 х2 + ε заменяя переменные х1 =х, х2 = х2, получим двухфакторное уравнение линейной регрессии: у= а0 + а1 х1 + а2 х2 + ε для оценки параметров которого используется МНК. Соответственно для полинома третьего порядка y= a0+a1x+a2x2+a3x3+ ε, при замене х=х1, х2=х2, х3=х3 получим трехфакторную модель линейной регрессии: у= а0 + а1 х1 + а2 х2 + а3 х3 + ε, Для полинома k-порядка y= a0+a1x+a2x2+…+akxk+ ε получим линейную модель множественной регрессии с k объясняющими переменными: у= а0 + а1 х1 + а2 х2 + …+ аk хk + ε Приравниваем к нулю первую производную параболы второй степени. Применение МНК для оценки параметров параболы второй степени приводит к следующей системе нормальных уравнений: Для равносторонней гиперболы такого вида, заменив 1/х на z, получим линейное уравнение регрессии оценка параметров которого может быть дана МНК. Система нормальных уравнений составит: В отдельных случаях может использоваться и нелинейная модель вида Но, если в равносторонней гиперболе преобразованию подвергается объясняющая переменная z = 1/x и y = а + bz + ε, то для получения линейной формы зависимости в обратной модели преобразовывается у, а именно: z =1/y и z = a + bx +ε. В результате обратная модель оказывается внутренне нелинейной и требование МНК выполняется не для фактических значений признака у, а для их обратных величин 1/у, а именно Видео:Нелинейная регрессия в MS Excel. Как подобрать уравнение регрессии? Некорректное значение R^2Скачать  Линеаризация
Модели, нелинейные по параметрам
в эконометрических исследованиях при изучении эластичности спроса от цен широко используется степенная функция: где у – спрашиваемое количество; ε – случайная ошибка. логарифмирование данного уравнения по основанию ε приводит его к линейному виду: lnу = lnа + b lnx + ln ε. Если же модель представить в виде то она становится внутренне нелинейной, т.к. ее невозможно превратить в линейный вид. Внутренне нелинейной будет и модель вида В этом плане к линейным относят, например, экспоненциальную модель т.к. логарифмируя ее по натуральному основанию, получим линейную форму модели lnу = а + b х +lnε. Модели внутренне нелинейные по параметрам могут иметь место в эконометрических исследованиях. Среди них можно назвать и обратную модель вида: В степенной функции параметр b является коэффициентом эластичности. Его величина, на сколько процентов изменится в среднем результат, если фактор изменится на 1%. Формула расчета коэффициента эластичности:
Если в линейной модели и моделях, нелинейных по переменным, при оценке параметров исходят из критерия то в моделях, нелинейных по оцениваемым параметрам, требование МНК применяется не к исходным данным результативного признака, а к их преобразованным величинам, т. е. lnу, 1/у. Так, в степенной функции y = axbε МНК применяется к преобразованному уравнению Это значит, что оценка параметров основывается на минимизации суммы квадратов отклонений в логарифмах: Соответственно, если в линейных моделях (включая нелинейные по переменным ∑(y-ŷх) =0, то в моделях, нелинейных по оцениваемым параметрам, Корреляция для нелинейной регрессии Для равносторонней гиперболы Линейный коэффициент корреляции между переменными y и lnx Ошибка разности между индексом детерминации R2yx и коэффициентом детерминации r2yx: Видео:Что такое полиномиальная регрессия? Душкин объяснитСкачать  Уравнение параболической регрессииВ некоторых случаях эмпирические данные статистической совокупности, изображенные наглядно с помощью координатной диаграммы, показывают, что увеличение фактора сопровождаются опережающим ростом результата. Для теоретического описания такого рода корреляционной взаимосвязи признаков можно взять уравнение параболической регрессии второго порядка: где Положив в основу вычисления параметров Из этих уравнений можно найти параметры Отсюда видно, что для определения параметров Допустим, имеются данные об удельном весе посевов картофеля в структуре всех посевных площадей и урожае (валовом сборе) культуры в 30 сельскохозяйственных организациях. Необходимо составить и решить уравнение корреляционной взаимосвязи между этими показателями. Т а б л и ц а 11.9. Расчет вспомогательных показателей для уравнения Параболической регрессии
Графическое изображение поля корреляции показало, что изучаемые показатели эмпирически связаны между собой линией, приближающейся к параболе второго порядка. Поэтому расчет необходимых параметров Т а б л и ц а 11.10. Расчет вспомогательных данных для уравнения Параболической регрессии
Подставим конкретные значения Σ у=495, Σ ху=600, Σ х 2 =750, Σ х 2 у=12375, Σ х 4 =18750, имеющиеся в табл. 11.10, в формулы (11.20), (11.21), (11.22). Получим Таким образом, уравнение параболической регрессии, выражающие влияние удельного веса посевов картофеля в структуре посевных площадей на урожай (валовой сбор) культуры в сельскохозяйственных организациях, имеет следующий вид: Уравнение 11.23 показывает, что в условиях заданной выборочной совокупности средний урожай (валовой сбор) картофеля (10 тыс. ц) может быть получен без влияния изучаемого фактора – повышения удельного веса посевов культуры в структуре посевных площадей, т.е. при таком условии, когда колебания удельного веса посевов не будут оказывать воздействие на размер урожая картофеля (х=0). Параметр (коэффициент пропорциональности) в=0,8 показывает, что каждый процент повышения удельного веса посевов обеспечивает прирост урожая в среднем на 0,8 тыс. т, а параметр с=0,1 свидетельствует о том, что на один процент (в квадрате) ускоряется приращение урожая в среднем на 0,1 тыс. т картофеля. 🔍 ВидеоРешение систем уравнений второго порядка. 8 класс.Скачать  МНК. Пример 2. Парная регрессияСкачать  РЕАЛИЗАЦИЯ ЛИНЕЙНОЙ РЕГРЕССИИ | Линейная регрессия | LinearRegression | МАШИННОЕ ОБУЧЕНИЕСкачать  Парная регрессия: парабола второго и третьего порядкаСкачать  Алгебра 9 класс (Урок№25 - Решение систем уравнений второй степени.)Скачать  Полиномиальная регрессияСкачать  Решение систем уравнений второй степениСкачать  Метод наименьших квадратов. Квадратичная аппроксимацияСкачать  Эконометрика. Линейная парная регрессияСкачать  Множественная степенная регрессияСкачать  Парная регрессия: линейная зависимостьСкачать  Лекция 8. Линейная регрессияСкачать  Решение систем уравнений второй степени | Алгебра 9 класс #19 | ИнфоурокСкачать  Эконометрика. Нелинейная регрессия. Степенная функция.Скачать  Эконометрика. Нелинейная регрессия. Гипербола.Скачать  |







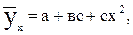 (11.16)
(11.16) , – параметр, показывающий среднее значение результативного признака при условии полной изоляции влияния фактора (х=0);
, – параметр, показывающий среднее значение результативного признака при условии полной изоляции влияния фактора (х=0);  – коэффициент пропорциональности изменения результата при условии абсолютного прироста признака-фактора на каждую его единицу; с – коэффициент ускорения (замедления) прироста результативного признака на каждую единицу фактора.
– коэффициент пропорциональности изменения результата при условии абсолютного прироста признака-фактора на каждую его единицу; с – коэффициент ускорения (замедления) прироста результативного признака на каждую единицу фактора.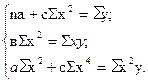
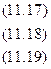
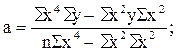 (11.20)
(11.20)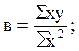 (11.21)
(11.21)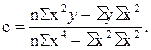 (11.22)
(11.22)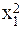
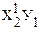
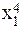
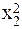
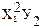
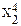
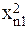
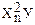
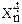
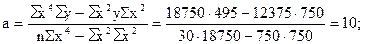
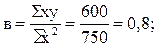
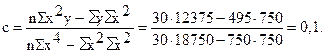
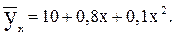 (11.23)
(11.23)