Уравнение ребер и граней сопровождающего трехгранника

Пространственные кривые. Задание пространственной кривой. Регулярное задание кривой. Регулярная кривая. Неявное задание пространственной кривой. Касательная к пространственной кривой. Единичный вектор касательной. Бинормаль и главная нормаль и их единичные векторы. Нормальная, соприкасающаяся и спрямляющая плоскости. Ускорение при криволинейном движении и векторы сопровождающего трехгранника. Кривизна пространственной кривой. Теорема о прямой. Кручение пространственной кривой. Теорема о плоской кривой. Формулы Френе. Естественный параметр и натуральные уравнения кривой.

Основные определения, результаты, комментарии

Элементарной кривой в пространстве называется образ открытого интервала при его гомеоморфизме в евклидово трехмерное пространство.

Общей кривой на плоскости называется подмножество евклидова пространства, локально гомеоморфное прямой.

Как и в случае плоских кривых, всякая общая кривая допускает покрытие элементарными кривыми.

Кривая задана неявным способом

если координаты каждой точки кривой удовлетворяют обоим уравнениям .

Наиболее удобны и наиболее часто используются векторно-параметрическое представление

и координатно-параметрическое представление

отличающиеся лишь формой записи.

Определение регулярности параметрического представления пространственной кривой полностью аналогично плоскому случаю.

Неявное задание (5) кривой регулярно в точке , если матрица частных производных

имеет в этой точке ранг 2.

Понятия длины кривой, ее естественной параметризации, а также определение касательной полностью аналогичны тем же понятиям для плоских кривых. Направляющий вектор касательной — это, по-прежнему, производная , имеющая физический смысл скорости, если параметрическое представление кривой интерпретировать как кинематическое описание движения точки.

Нормальная плоскость кривой в точке — это плоскость, проходящая через точку ортогонально касательной.

Соприкасающейся плоскостью кривой в ее точке (рис. 17) называется содержащая эту точку плоскость , удовлетворяющая соотношению

где — точка, принадлежащая элементарной окрестности точки .

Спрямляющей плоскостью кривой в ее точке называется содержащая эту точку плоскость, ортогональная нормальной и соприкасающейся плоскостям в этой точке.

Прямые, ортогональные соприкасающейся и спрямляющей плоскостям в точке , называются соответственно бинормалью и главной нормалью кривой в точке .

Нормальная, соприкасающаяся и спрямляющая плоскости образуют сопровождающий трехгранник кривой , или трехгранник Френе , в точке , и называются его гранями . Касательная, бинормаль и главная нормаль называются ребрами сопровождающего трехгранника (рис. 18).

Уравнения элементов сопровождающего трехгранника вычисляются по следующим правилам:

Касательная	Нормальная плоскость
Бинормаль	Соприкасающаяся плоскость
Главная нормаль	Спрямляющая плоскость

Единичные векторы

касательной

главной нормали

бинормали

Если параметризация естественная , то вектор главной нормали может быть вычислен по формуле .

Вектор ускорения может быть разложен в сумму двух составляющих: нормальной (ортогональной вектору скорости) и тангенциальной (параллельной вектору скорости). При этом нормальная составляющая ускорения сонаправлена единичному вектору главной нормали.

Пусть и — две различные точки кривой , соответствующие значениям и естественного параметра. Тогда — длина дуги кривой, заключенной между точками и . Пусть — величина угла, образуемого касательной к кривой в точке по отношению к касательной в точке . Кривизна кривой в ее точке — это предел

В отличие от кривизны плоской кривой, кривизна пространственной кривой всегда положительна . Кривизна пространственной кривой в регулярной точке может быть вычислена по формулам:

если параметризация естественная.

Пусть и — две различные точки кривой , соответствующие значениям естественного параметра и соответственно, и — единичные векторы бинормалей в этих точках (рис. 19).

Обозначим за величину угла между ними. Очевидно, этот угол равен углу, образованному соприкасающимися плоскостями в точках и .

Абсолютным кручением кривой в точке называют величину

Кручение кривой определяется в соответствии со следующим правилом: если при движении вдоль кривой по направлению возрастания параметра вектор бинормали поворачивается в сторону, указываемую вектором , в противном случае. Наглядно это означает, что кривая с положительным кручением «закручена» по правилу правого винта.

Кручение кривой в точке, соответствующей значению параметра , может быть вычислено по следующим формулам:

Для производных векторов , по естественному параметру справедливы формулы Френе :

Уравнения и называются натуральными уравнениями кривой. По натуральным уравнениям вид кривой может быть восстановлен с точностью до перемещения. В большинстве случаев решение такой задачи оказывается очень сложным.

1. Для данных представлений кривых укажите область допустимых значений параметра и область значений параметра, в которой задание кривой регулярно.
1)
2)
3)
4) .

2. Кривая задана неявными уравнениями. Изобразите на рисунке вид кривой. Постройте какое-нибудь параметрическое представления этой кривой. Укажите область допустимого изменения параметра и область регулярности параметризации.
1)
2) R,;; y>0;$ —> R,;; y>0;$»>
3)

3. Кривая Вивиани образована пересечением сферы радиуса и цилиндра радиуса , проходящего через центр сферы. Постройте параметрическое представление кривой Вивиани.

4. Винтовая линия. Окружность радиуса движется так, что ее центр перемещается вдоль оси , плоскость ортогональна оси . По окружности равномерно движется точка. В начальный момент времени точка имеет координаты . Составьте параметрические уравнения кривой, описываемой данной точкой.

5. Кривая задана пересечением цилиндрических поверхностей и Постройте параметрическое представление кривой , не содержащее радикалов, и дайте ее изображение.

6. Покажите, что линия

принадлежит сфере и является линией пересечения параболического и кругового цилиндров.

7. Найдите длину дуги линии

между плоскостями и .

8. Покажите, что кривая замкнута и имеет длину .

9. Запишите в естественной параметризации
a) винтовую линию ;
б) гиперболическую винтовую линию .

10. Кривая задана параметрически: 0. end —>

Напишите уравнения
а) касательной и нормальной плоскости в точке (1/4; 1/3; 1/2);
б) касательной, параллельной плоскости .

11. Найдите линию, по которой касательные к линии

Сферической индикатрисой данной кривой называется геометрическое место концов единичных касательных векторов, отложенных от начала координат.

12. Дана винтовая линия

a) Напишите уравнение семейства касательных этой кривой;
б) убедитесь в том, что все касательные к винтовой линии образуют с плоскостью один и тот же угол;
в) составьте уравнение кривой, образуемой точками пересечения касательных с плоскостью ;
г) найдите сферическую индикатрису винтовой линии.

13. Докажите, что все нормальные плоскости кривой Вивиани (задача 3) проходят через начало координат.

14. Составьте уравнения бинормали и главной нормали кривой в указанной точке:
1)
2)
3) ;
4)

15. Найдите точки на кривой

в которых бинормаль параллельна плоскости .

16. Материальная точка движется в пространстве по закону

Укажите моменты времени, в которые
а) ее скорость равна нулю, и сравните их со значениями параметра , при которых параметризация траектории нерегулярна;
б) нормальное ускорение точки ортогонально .

17. Составьте уравнения ребер и граней сопровождающего трехгранника данной кривой в указанной точке
1)
2)
3)
4)

18. Для данной кривой вычислите кривизну в данной точке сначала по готовой формуле, а затем по следующему плану: 1) составьте уравнение поля единичных касательных векторов данной кривой; 2) вычислите абсолютную величину производной этого поля по естественному параметру. Результаты сравните.
1) 0,;; bne 0, ;; t_0=pi/2$ —> 0,;; bne 0, ;; t_0=pi/2$»>
2)

19. Для кривых задачи 18 вычислите абсолютное кручение в данной точке сначала по готовой формуле, а затем по следующему плану: 1) составьте уравнение поля единичных векторов бинормали данной кривой; 2) вычислите абсолютную величину производной этого поля по естественному параметру. Результаты сравните.

20. Вычислите кривизну и кручение данной кривой произвольной регулярной точке:
1) 0,;; bne 0$ —> 0,;; bne 0$»>;
2)
3)
4) .

21. Найдите точки распрямления следующих кривых:
1)
2)
3) .

22. Найдите точки уплощения и дуги, на которых кручение сохраняет свой знак, у следующих кривых:
1)
2)

23. Напишите натуральные уравнения, которым удовлетворяют следующие кривые:
1) 0,;; bne 0$ —> 0,;; bne 0$»>;
2)

24. Найдите точки на кривой

в которых кривизна принимает локально минимальное значение.

25. Найдите точки на кривой

в которых радиус кривизны достигает локального максимума.

26. Докажите, что следующие кривые плоские, и составьте уравнения плоскостей, в которых они расположены:

27. Найдите такую функцию , чтобы кривая

была плоской. Решите задачу двумя способами: 1) используя условие плоскости и 2) используя тот факт, что искомая кривая принадлежит круговому цилиндру (составьте его уравнение!). Результаты сравните.

28. Докажите, что если все соприкасающиеся плоскости линии проходят через неподвижную точку , то линия плоская.

29. Докажите, что если соприкасающиеся плоскости линии (отличной от прямой) параллельны некоторому вектору , то линия плоская.

30. Докажите, что если все нормальные плоскости линии параллельны некоторому вектору , то линия или прямая, или плоская.

Сопровождающий трехгранник кривой

Пусть (Gamma) — дважды дифференцируемая кривая без особых точек, для которой выполняются условие, описанное здесь ((displaystylefracneq 0)). Тогда выполняются это и это равенства, где (boldsymboltau) — единичный вектор касательной, (nu) — единичный вектор нормали к кривой (Gamma) в данной ее точке.

Рассмотрим вектор
$$
boldsymbolbeta=[boldsymboltau,boldsymbolnu].label
$$

Тогда (boldsymbolbeta) — единичный вектор, ортогональный векторам (boldsymboltau) и (boldsymbolnu):
$$
boldsymboltau=[boldsymbolnu,boldsymbolbeta],qquad boldsymbolnu=[boldsymbolbeta,boldsymboltau].label
$$

Прямую, проходящую через точку кривой параллельно вектору (boldsymbolbeta), называют бинормалью. Тетраэдр с вершиной в точке кривой, ребра которого имеют длину, равную единице, и параллельны векторам (boldsymbol), называют сопровождающим трехгранником Френе (рис. 22.12).

Рис. 22.12

Если (Gamma) — трижды непрерывно дифференцируемая кривая, удовлетворяющая данному условию, то справедливы формулы Френе
$$
frac=kboldsymboleta,nonumber
$$
$$
frac=-kboldsymboltau+varkappaboldsymbolbeta,label
$$
$$
frac=-varkappaboldsymbolnu.label
$$

(circ) Первая из формул Френе получена здесь. Докажем формулу eqref. Дифференцируя равенство eqref с учетом первой формулы Френе и равенства ([boldsymbolnu,boldsymbolnu]=0), получаем
$$
frac=left[frac,boldsymbolnuright]+left[boldsymboltau,fracright]=left[boldsymboltau,fracright].nonumber
$$

Так как (boldsymbolnu) — единичный вектор, то он ортогонален вектору (displaystyle frac). Кроме того, вектор (boldsymbolnu) ортогонален вектору (boldsymboltau). Поэтому вектор (left[tau,displaystyle fracright]) параллелен вектору (boldsymbolnu) и справедливо равенство eqref. Коэффициент (varkappa) в формуле eqref называют кручением кривой в данной ее точке.

Пользуясь первой формулой Френе, формулами eqref, eqref и eqref, получаем
$$
frac=left[frac,boldsymboltauright]+left[boldsymbolbeta,fracright]=-varkappa[boldsymbolnu,boldsymboltau]+k[boldsymbolbeta,boldsymbolnu]=-kboldsymboltau+varkappaboldsymbolbeta,nonumber
$$
то есть справедлива формула eqref. (bullet)

Докажем, наконец, следующее: если кривая, заданная натуральным уравнением, трижды дифференцируема, а ее кривизна (k=k(s)) отлична от нуля, то кручение кривой (varkappa=x(s)) выражается формулой
$$
varkappa=frac<left(frac<dtextbf>,frac<d^textbf><ds^>,frac<d^textbf><ds^>right)><k^>.label
$$
(circ) Используя первую формулу Френе и eqref, находим
$$
frac<d^textbf><ds^>=k(s)boldsymbolnu,quad frac<d^textbf><ds^>=k'(s)boldsymbolnu+k(s)frac=k'(s)boldsymbolnu-k^(s)boldsymboltau+k(s)varkappa(s)boldsymbolbeta.nonumber
$$
Вычислим смешанное произведение векторов, указанных в формуле eqref, пользуясь тем, что ((boldsymboltau,boldsymbolnu,boldsymbolnu)=(boldsymboltau,boldsymbolnu,boldsymboltau)=0) и ((boldsymboltau,boldsymbolnu,boldsymbolbeta)=1). Тогда из равенства
$$
left(frac<dtextbf>,frac<d^textbf><ds^>,frac<d^textbf><ds^>right)=(boldsymboltau,k(s)boldsymbolnu,k'(s)boldsymbolnu-k^(s)boldsymboltau+k(s)varkappa(s)boldsymbolbeta)=\=k^(s)varkappa(s)(boldsymboltau,boldsymbolnu,boldsymbolbeta)=k^(s)varkappa(s)nonumber
$$
следует формула eqref. (bullet)

Из формулы eqref следует, что (left|displaystyle fracright|=|varkappa|), так как (|nu|=1). Повторяя рассуждения, связанные с выяснением физического смысла кривизны кривой, отсюда получим, что
$$
|varkappa|=lim_left|fracright|,label
$$
где (Deltaalpha) — угол поворота бинормали к кривой (Gamma) при изменении ее параметра от (s) до (s+Delta s). Выражение в правой части eqref назовем скоростью вращения вектора бинормали. Эта скорость равна скорости вращения соприкасающейся плоскости кривой, так как вектор (boldsymbolbeta) перпендикулярен этой плоскости. Таким образом, модуль кручения кривой равен скорости вращения соприкасающейся плоскости.

Вычислим кривизну (k) и кручение (varkappa) винтовой линии:
$$
x=acos t,quad y=asin t,quad z=bt,quad 0leq tleq T,nonumber
$$
где (a > 0, b > 0)

(triangle) В примере получено натуральное уравнение винтовой линии
$$
textbf=textbf(s)=(acoslambda s,asinlambda s,blambda s),nonumber
$$
где
$$
lambda=frac<sqrt<a^+b^>>.nonumber
$$

Для нахождения (varkappa) воспользуемся формулой eqref, а вектор (boldsymbolbeta) найдем по формуле eqref. Имеем
$$
boldsymbolbeta=(blambdasinlambda s,-blambdacoslambda s,alambda),nonumber
$$
откуда
$$
frac=(blambda^cos lambda s,blambda^sinlambda s,0)=-blambda^(-coslambda s,-sinlambda s,0),nonumber
$$
то есть
$$
frac=-blambda^boldsymbolnu,nonumber
$$
отсюда по формуле eqref находим
$$
varkappa=blambda^2=frac<a^+b^>.nonumber
$$
Таким образом, кривизна кривой и кручение для винтовой линии постоянные. (blacktriangle)

Лекция Пространственные кривые. Сопровождающий трехгранник кривой. Формулы френе. Эволюта и эвольвента пространственной кривой

2.4 СОПРОВОЖДАЮЩИЙ ТРЕХГРАННИК КРИВОЙ.

Рассмотрим кривую в натуральной параметризации:

Г:

в окрестности точки . Здесь и далее в скобках приводятся соответствующие формулы для произвольного параметра. Наряду с точкой М_орассмотрим ещё две соседних точкиМ₁и М₂. Выше мы вводили понятие касательной, как предельное положение секущей М_оМ₁при М₁®М_о. Напомним, что вектор

(2.8)

‑единичный вектор касательной, направленный в сторону возрастания параметраs.

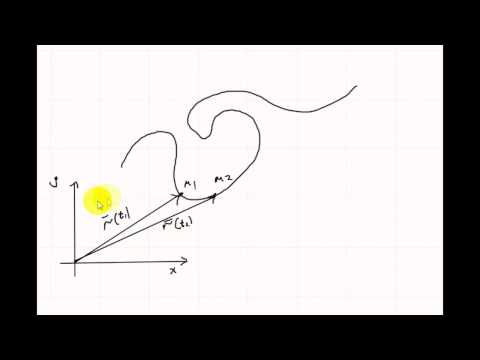
Определение 2.1Кругом кривизны кривой Г в точке М_оназывается предельное положение окружности, проходящей через точки М_о, М₁и М₂при М₁®М_оиМ₂®М_о. Радиус этой окружности называется радиусом кривизны, а её центр С – центром кривизны кривой Г в точке М_о.

Заметим, что радиус кривизны вычисляется по формуле

(2.9)

(2.9’)

называется кривизной кривой Г.

Определение 2.2Главной нормалью кривой Г в точке М_оназывается направленная прямая, идущая из точки М_ов центр круга кривизны.

Единичный вектор главной нормали находится по формуле:

(2.10)

или (2.10’)

Определение 2.3Бинормалью кривой Г в точке М_оназывается направленная прямая, проходящая через точку М_ои образующая вместе с положительной касательной и главной нормалью правую тройку, которая называется репером Френе (иногда — сопровождающим трёхгранником).

Единичный вектор бинормали находится по формуле:

(2.11)

или (2.11’)

Определение 2.3Нормальной плоскостью называется плоскость, перпендикулярная касательной. Спрямляющей плоскостью называется плоскость, перпендикулярная главной нормали. Соприкасающейся плоскостью называется плоскость, перпендикулярная бинормали. Эти три плоскости иногда называют сопровождающим трёхгранником кривой.

2.4 ФОРМУЛЫ ФРЕНЕ

Единичные векторы касательной, нормали и бинормали связаны формулами Френе (без доказательства):

(2.12)

(2.13)

(2.14)

Здесь — кривизна, а величина

(2.15)

или (2.15’)

называется кручением кривой Г в точке М.

Точки, где кривизна кривой равна нулю, называются точками распрямления, а точки, в которых кручение равно нулю, называются точками уплощения.

Для того, чтобы кривая была плоской, необходимо и достаточно, чтобы кручение в каждой её точке было равно нулю.

2.4ЭВОЛЮТА И ЭВОЛЬВЕНТА ПРОСТРАНСТВЕННОЙ КРИВОЙ

Определение 2.5Эволютойgкривой Г: называется геометрическое место центров кривизны этой кривой.

Для получения уравнения эволютыgзаметим, что , значит уравнение эволютыgимеет вид: (2.17)

Определение 2.6Если криваяgявляется эволютой кривой Г, то кривая Г называется эвольвентой кривойg.

а) единичные векторы касательной, нормали, бинормали;

б) уравнения касательной, нормали и бинормали;

в) уравнения нормальной, соприкасающееся и спрямляющей плоскостей;

г) кривизну и кручение;

д) составить уравнение эволюты.

а) Точке М_о(1, 0, 0) соответствует значение параметраt_o=0. Найдём производные радиус-вектора в этой точке:

Найдём единичные векторы касательной, главной нормали и бинормали: ;

;

;

;

б) Поскольку вектор является направляющим вектором касательной, вектор — направляющим вектором главной нормали, а вектор — бинормали, запишем для точки М_о(1, 0, 0) канонические уравнения касательной:

,главной нормали:

и бинормали: .

в) Нормальная плоскость проходит через точку М_о(1, 0, 0) перпендикулярно вектору касательной , её уравнение: .

Соприкасающаяся плоскость проходит через точку М_о(1, 0, 0) перпендикулярно вектору бинормали , её уравнение: .

Спрямляющая плоскость проходит через точку М_о(1, 0, 0) перпендикулярно вектору нормали , её уравнение: .

г) Кривизна по формуле (2.9’): , .

Кручение найдём по формуле (2.15’): .

д) Уравнение эволюты найдём по формуле (2.17): .

Здесь ; .

Найдём , ,

,

.

Отсюда следует, что кривизна и кручение в точках винтовой линии имеют постоянное значение, .

Подставим найденное в формулу (2.17):

,

т.е. эволютой винтовой линии будет так же винтовая линия, но повёрнутая вокруг осиOzна 180°.

🌟 Видео