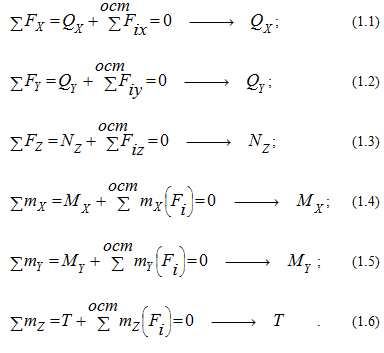Уравнение равновесия внутренних усилий действующих в сечении (3 видео)

Техническая механика

Содержание

Сопротивление материалов
Метод сечений. Напряжения
Сущность метода сечений
Напряжение
Дифференциальные уравнения равновесия для внутренних усилий в поперечных сечениях стержней
iSopromat.ru
Правила знаков для внутренних силовых факторов
Эпюры внутренних силовых факторов
💡 Видео

Сопротивление материалов

Видео:Сопромат. Часть 1. Растяжение (сжатие). Построение эпюр продольных сил и нормальных напряжений.Скачать

Метод сечений. Напряжения

Сущность метода сечений

Для расчетов элементов конструкции на прочность необходимо знать внутренние силы упругости, возникающие в результате приложения внешних сил в разных точках и частях конструкции.
Но как заглянуть внутрь материального тела, чтобы выяснить, какие же силы возникают между его частицами или отдельными частями, при приложении нагрузок? Представление о внутренних усилиях, возникающих в теле или элементе конструкции можно получить лишь с помощью воображения и аксиом статики, поясняющих условия равновесного состояния материальных тел.
Способы определения этих внутренних сил с помощью науки сопротивление материалов включают такой прием, как метод сечений .

Метод сечений заключается в том, что тело мысленно рассекается плоскостью на две части, любая из которых отбрасывается и взамен ее к сечению оставшейся части прикладываются внутренние силы, действовавшие на нее до разреза со стороны отброшенной части. Оставленная часть рассматривается как самостоятельное тело, находящееся в равновесии под действием приложенных к сечению внешних и внутренних сил (третий закон Ньютона – действие равно противодействию).
При применении этого метода выгоднее отбрасывать ту часть элемента конструкции (тела), для которой проще составить уравнение равновесия. Таким образом, появляется возможность определить внутренние силовые факторы в сечении, благодаря которым оставшаяся часть тела находится в равновесии (прием, часто применяемый в Статике).

Применяя к оставленной части тела условия равновесия, невозможно найти закон распределения внутренних сил по сечению, но можно определить статические эквиваленты этих сил (равнодействующие силовые факторы).
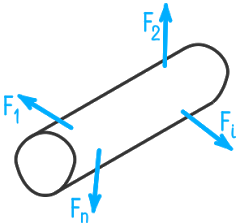
Так как основным расчетным объектом в сопротивлении материалов является брус, рассмотрим, какие статические эквиваленты внутренних сил проявляются в поперечном сечении бруса.

Рассечем брус (рис. 1) поперечным сечением а-а и рассмотрим равновесие его левой части.
Если внешние силы, действующие на брус, лежат в одной плоскости, то в общем случае статическим эквивалентом внутренних сил, действующих в сечении а-а , будут главный вектор F_гл , приложенный в центре тяжести сечения, и главный момент М_гл = М_и , уравновешивающие плоскую систему внешних сил, приложенных к оставленной части бруса.

Разложим главный вектор на составляющую N , направленную вдоль оси бруса, и составляющую Q , перпендикулярную этой оси и лежащую в плоскости сечения. Эти составляющие главного вектора и главный момент называют внутренними силовыми факторами , действующими в сечении бруса. Составляющую N называют продольной силой , составляющую Q – поперечной силой , пару сил с моментом М_и – изгибающим моментом .

Для определения указанных трех внутренних силовых факторов применим известные из Статики уравнения равновесия оставленной части бруса:

Σ Z = 0; Σ Y = 0; Σ M = 0; (ось z всегда направляем по оси бруса).

Если внешние силы, действующие на брус, не лежат в одной плоскости, т. е. представляют собой пространственную систему сил, то в общем случае в поперечном сечении бруса возникают шесть внутренних силовых факторов (рис. 2) , для определения которых применяют известные из Статики шесть уравнений равновесия оставленной части бруса:

Σ X = 0; Σ Y = 0; Σ Z = 0;
Σ M_x = 0; Σ M_y = 0; Σ M_z = 0 .

Эти силовые факторы в общем случае носят следующие названия: N – продольная сила, Q_x , Q_y – поперечные силы, М_кр – крутящий момент, М_их и М_иу – изгибающие моменты.

При разных деформациях в поперечном сечении бруса возникают различные силовые факторы.
Рассмотрим частные случаи:

1. В сечении возникает только продольная сила N . Это деформация растяжения (если N направлена от сечения) или сжатия (если N направлена к сечению).

2. В сечении возникает только поперечная сила Q . Это деформация сдвига .

3. В сечении возникает только крутящий момент М_кр . Это деформация кручения .

4. В сечении возникает только изгибающий момент М_и . Это деформация чистого изгиба . Если в сечении одновременно возникает изгибающий момент М_и и поперечная сила Q , то изгиб называют поперечным .

5. Если в сечении одновременно возникает несколько внутренних силовых факторов (например, изгибающий момент и продольная сила), то имеет место сочетание основных деформаций (сложное сопротивление).

Напряжение

Наряду с понятием деформации одним из основных понятий сопротивления материалов является напряжение (обозначается р ).
Напряжение характеризует интенсивность внутренних сил, действующих в сечении, и определяется, как отношение величины внутренней силы к площади сечения.
Напряжение является величиной векторной.

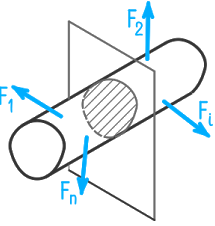
Вектор напряжения можно разложить на две составляющие (рис. 3) – одну вдоль оси сечения, вторую – в плоскости сечения (перпендикулярно оси). Эти составляющие носят название нормальное напряжение (обозначается σ) и касательное напряжение (обозначается τ ).
Поскольку нормальные и касательные напряжения расположены под прямым углом друг к другу, модуль полного напряжения p можно определить по теореме Пифагора:

Единица измерения напряжения – паскаль (Па).
1 Па = Н / м 2 . Поскольку эта единица очень мала, в расчетах часто применяют более крупную кратную единицу – мегапаскаль (МПа), который равен миллиону паскалей (10 6 Па).

Объяснить сущность напряжения можно на таком простом примере.
В соответствии с гипотезой об отсутствии первоначальных внутренних усилий, считается, что когда к телу не приложены внешние нагрузки его частицы не взаимодействуют друг с другом, т. е. абсолютно равнодушны к «соседкам» справа, слева и т. п. Но стоит приложить к телу внешнюю нагрузку, его частицы начинают лихорадочно цепляться друг за друга, пытаясь удержаться в «кучке». Если нагрузка растягивает тело, его частицы держатся друг за дружку, не давая разорвать тело, если нагрузка сжимающая — частицы тела стараются удержать «соседок» на прежнем расстоянии.
Совокупность всех этих усилий внутренних частиц, противостоящих внешним раздражителям-нагрузкам, и является напряжением.
Задачи сопромата чаще всего сводятся к тому, чтобы определить предельные величины нагрузок, способных разорвать связи между частицами, из которых состоит тело или, по известным предельным напряжениям определить, какие нагрузки способно выдержать тело не разрушаясь, не деформируясь и т. д.

Нетрудно заметить, что напряжение измеряется в тех же единицах, что и давление, поэтому можно провести некоторую аналогию между этими физическими понятиями. Принципиальная разница заключается в том, что давление — внешний силовой фактор (т. е. воздействующий на тело или его части извне), а напряжение — внутренний силовой фактор, характеризующий степень взаимодействия (взаимосвязи) частиц тела между собой.

Видео:Основы Сопромата. Внутренние силы. Эпюры внутренних усилий для пространственного стержняСкачать

Дифференциальные уравнения равновесия для внутренних усилий в поперечных сечениях стержней

В общем случае нагрузка на стержень может быть задана интенсивностью сил с составляющими , и интенсивностью моментов с составляющими . Возможна также нагрузка, сосредоточенная в отдельных точках. Для бесконечно малой части стержня (рис.2.3) составим дифференциальные уравнения равновесия.

Из условий следуют уравнения:

Из условий получаем:

откуда, пренебрегая бесконечно малыми второго порядка, находим

Подставляя выражения в соответствующие дифференциальные уравнения, получаем

Интегрируя полученные шесть уравнений, находим выражения для внутренних усилий:

Постоянные интегрирования С_i (i=1,2. 6) определяются из граничных условий для рассматриваемых внутренних усилий.

Поскольку дифференциальные уравнения выражают равновесие любого бесконечно малого элемента стержня, то удовлетворение им означает выполнение условий равновесия стержня в целом.

Дифференциальные зависимости используются для проверки результатов, полученных с помощью алгебраических уравнений равновесия. Они позволяют, например, по эпюре определить характер эпюры . В частности, на участках, где =0 (=0), т.е. при соблюдении зависимостей

можно установить, что при М_z = const имеем Q_y = 0(при М_y =const имеем Q_z = 0). Переменная величина достигает экстремальных значений в точках, где Q_y = 0(Q_z = 0).

При определении внутренних усилий из уравнений равновесия целесообразно нагрузку на поверхности переносить в соответствующие точки на оси стержня с соблюдением условий статической эквивалентности. Полученная таким образом силовая схема является составной частью так называемой расчетной схемы (системы), когда брус представляется его осью.

Дата добавления: 2015-05-28 ; просмотров: 930 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:СМ -1.7 Метод сечений, внутренние силовые факторы (ВСФ)Скачать

iSopromat.ru

Внутренние силовые факторы (усилия) возникают в результате деформации бруса, когда под действием внешних нагрузок происходит изменение взаимного расположения элементарных частиц тела.

По своей природе внутренние силовые факторы представляют собой взаимодействие частиц тела, обеспечивающее его целостность и совместность деформаций. Для определения этих усилий применяют метод сечений:

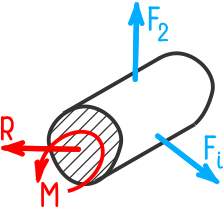
надо мысленно рассечь брус, находящийся в равновесии, на две части

и рассмотреть равновесие одной из них.

Действие усилий отброшенной части бруса заменим уравновешивающими рассматриваемую часть внутренней силой R и внутренним моментом M.

Для упрощения расчетов силу R и момент M принято раскладывать на составляющие усилия относительно осей координат x, y и z.

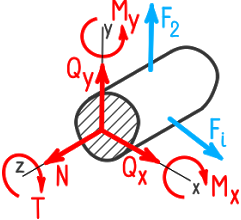
Таким образом, под действием внешних нагрузок в поперечном сечении бруса могут возникать следующие внутренние силовые факторы:

N_z = N — продольная растягивающая (сжимающая) сила;
M_z = T — крутящий (скручивающий) момент;
Q_x (Q_y) = Q — поперечные силы;
M_x (M_y) = M — изгибающие моменты.

Каждый внутренний силовой фактор определяется из соответствующего уравнения равновесия оставшейся после рассечения бруса части (уравнения статики):

Наш видеоурок построения эпюр внутренних силовых факторов для балки:

Видео:Сопротивление материалов. Лекция: метод сеченийСкачать

Правила знаков для внутренних силовых факторов

Для определения знаков внутренних усилий, возникающих в брусе при различных способах его нагружения, приняты следующие правила:

при растяжении/сжатии — положительными являются растягивающие усилия;
при кручении — положительны моменты, стремящиеся повернуть рассматриваемую часть вала против хода часовой стрелки;
при изгибе — положительны моменты сжимающие верхний слой балки.

Видео:Основы Сопромата. Задача 1. Растяжение-сжатие стержняСкачать

Эпюры внутренних силовых факторов

В инженерной практике особое место занимает умение ясно представить взаимодействие усилий в конструкции, а также связь между внешними и внутренними силами в элементах конструкции, для этого графически изображают внутренние силовые факторы в функции осевой координаты и называют эти графики — эпюрами.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах