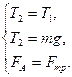Уравнение равновесия сил при равномерном падении шарика в вязкой жидкости (6 видео)

Рассмотрим падение шарика в вязкой жидкости

При движении шарика слой жидкости, граничащий с его поверхностью, прилипает к шарику и движется со скоростью шарика. При вычислении сопротивления среды следует учитывать трение отдельных слоев жидкости друг о друга, а не трение шарика о жидкость.

На шарик, падающий в вязкой жидкости, действуют три силы (рис. 2.2):

· сила тяжести F₁= mg = p_ш×V×g;

· сила Архимеда F_А = p_ж×V×g (равная весу жидкости в объеме шарика);

· сила сопротивления, обусловленная вязкостью жидкости:

F = 6p×h×r×v,

где r_ш – плотность материала шарика;

r_ж – плотность жидкости;

V – объем шарика;

g – ускорение свободного падения.

Все три силы направлены по вертикали: F₁ – вниз, F₂ и F₃ – вверх.

В общем случае уравнение движения шарика имеет вид

Сила сопротивления с увеличением скорости движения шарика возрастает, а ускорение dv/dt уменьшается до тех пор, пока шарик не достигнет такой скорости, при которой ускорение равно 0.

Тогда уравнение (2.3) примет вид:

в этом случае шарик движется с постоянной скоростью v₀.

Решая (2.4) относительно h, получим

(2.5)

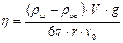
Если теперь учесть, что V = r 3 , r = d/2, v₀ = l/t,

где d – диаметр шарика;

l – длина участка равномерного движения, пройденного за время t,

то формула (2.5) примет окончательный вид

(2.6)

Таким образом, для нахождения h нужно измерить d, l и t.

Рассмотрим подъем шарика в вязкой жидкости.

Если два одинаковых шарика связаны невесомой нитью, перекинутой через блок, причем один из шариков будет погружен в сосуд с жидкостью (2.3.), то уравнения движения шарика имеют вид:

(2.7)

В уравнениях (2.7)

I – момент инерции диска;

R – радиус диска;

Т₁ и Т₂ – натяжение нитей,

F_тр – сила трения, обусловленная вязкостью жидкости,

F_А – сила Архимеда.

Сила сопротивления с увеличением скорости движения шарика возрастает, а ускорение уменьшается до тех пор, пока шарик не достигнет такой скорости v₀, при которой ускорение равно 0.

Тогда уравнения (2.7), при , принимают вид:

В этом случае шарик двигается с постоянной скоростью. Из (2.8) следует

(2.9)

или аналогично формуле (2.6) расчетная формула принимает вид:

(2.10)

В формуле (2.10) так же как и в формуле (2.6) нужно измерить d, l, t.

Описание установки.

Длинный стеклянный цилиндр, наполненный исследуемой жидкостью, имеет две горизонтальные метки А и В, расположенные на расстоянии l друг от друга. Метка А установлена так, что при прохождении через нее шарик уже имеет постоянную скорость v₀ (см. рис 2.2).

При измерении вязкости при подъеме шарика применяется схема (рис. 2.3): на краю стеклянного цилиндра установлен блок, через который перекинуты шарики, связанные нитью. Для определения вязкости при подъеме шарика, один шарик опускают на дно цилиндра с жидкостью.

Видео:Урок 137. Движение тела в жидкости и газе.Скачать

Движение шарика в вязкой среде

Когда тело из твердого материала движется в жидкости, жидкость вынуждена обтекать его. Слой жидкости, прилегающий к поверхности тела, обычно движется вместе с ним, а жидкость на большом удалении от тела покоится. Поэтому в окружении тела существует градиент скорости, в котором диссипирует энергия движения. Это значит, что на движущееся тело действует сила гидродинамического сопротивления. При малых скоростях течения она пропорциональна скорости движения с коэффициентом пропорциональности /, который зависит от размера и формы тела и от вязкости среды. В гидродинамике доказывается, что для сферического тела радиусом г, движущегося поступательно (без вращения) с небольшой скоростью, коэффициент трения /равен бщг, т.е. сила вязкого сопротивления при медленном движении шарика в текучей среде составляет

Это уравнение называют формулой Стокса (G.G. Stokes, 1851).

Когда шарик падает под действием силы тяжести в жидкости, на него действуют силы: 1) собственно сила тяжести /(тяж) = mg 2) выталкивающая сила, равная весу жидкости, которую шарик вытесняет своим объемом /(выт); 3) сила вязкого сопротивления (10.21). Если направление вниз по вертикали считать положительным, то выражение для равнодействующей силы имеет вид F= /(тяж) — /(выт) — /(сопр). Выталкивающая сила равна произведению массы жидкости т₀, которую шарик вытесняет своим объемом, и ускорения свободного падения: /’(выт) = т$, где g — ускорение свободного падения. Таким образом, F = mg — т$ — fv. Разность т-т₀ называют эффективной массой и обозначают т_эфф. То есть эффективная масса — это масса тела, исправленная на массу среды, которую тело вытесняет своим объемом. Таким образом, баланс сил имеет вид:

Если в начальный момент времени шарик покоится, а затем падает, то скорость, конечно, увеличивается под действием силы тяжести. В результате увеличивается сила сопротивления жидкости, но сила тяжести m_effg остается постоянной. Поэтому может быть достигнута скорость, при которой равнодействующая сила в (10.22) равна нулю. Тогда шарик продолжит падение с постоянной скоростью v_s. Ее называют скоростью стационарного или установившегося движения:

Из этого следует выражение для стационарной скорости падения:

Эффективная масса шарика выражается через его объем V= 4%j/3, плотность р материала шарика и р₀ среды, в которой он падает:

Тогда из уравнений (10.24), (10.25), (10.21) следует формула

Она верна при условии, что стационарная скорость не настолько велика, чтобы вызвать завихрения в жидкости при обтекании шарика, и что шарик не вращается при движении. При выполнении этих условий можно вычислить вязкость, если известно время /, за которое шарик проходит известный путь L в стационарном режиме:

В действительности для измерения вязкости жидкостей обычно применяется не свободное падение шарика, а его скатывание по внутренней цилиндрической стенке сосуда, в котором находится жидкость. Такой прибор называют вискозиметром Хепплера. В нем скорость скатывания зависит от трения качения по стенке и от угла наклона вискозиметра. Для определения вязкости время скатывания шарика в приборе калибруют с помощью жидкостей с известными величинами вязкости. Затем вязкость испытуемой жидкости вычисляют из времени скатывания и коэффициента, найденного предварительной калибровкой прибора.

Видео:Вязкость. Ламинарное и турбулентное течения жидкостей. 10 класс.Скачать

Теория метода и описание установки

Метод Стокса, используемый в данной работе, заключается в следующем.

На твердый шарик, падающий в вязкой жидкости, действуют три силы: сила тяжести, выталкивающая и сила сопротивления движению, обусловленная силами внутреннего трения жидкости (рисунок 2).

Рисунок 2. Силы, действующие на шарик, падающий в жидкости

При движении шарика слой жидкости, граничащий с его поверхностью, прилипает к шарику и движется со скоростью шарика. Ближайшие смежные слои жидкости также приводятся в движение, но получаемая ими скорость тем меньше, чем дальше они находятся от шарика.

Сила внутреннего трения по закону Стокса равна:

где — коэффициент внутреннего трения жидкости, — скорость шарика, — его радиус.

Сила тяжести равна:

где — плотность вещества шарика, — объем шарика.

Выталкивающая сила (по закону Архимеда) равна:

где — плотность жидкости.

Указанные три силы направлены по вертикали: сила тяжести — вниз, выталкивающая сила и сила трения — вверх.

На основании второго закона Ньютона уравнение движения в случае падения шарика в жидкости имеет вид:

закон вязкость сопротивление

Сила сопротивления с увеличением скорости движения шарика возрастает, а ускорение уменьшается и, наконец, шарик достигает такой скорости, при которой ускорение становится равным нулю, тогда уравнение (5) принимает вид:

В этом случае шарик движется с постоянной скоростью . Такое движение шарика называется установившимся. Решая уравнение (6) относительно коэффициента внутреннего трения, получим

Формула (7) справедлива для шарика, падающего в безгранично простирающейся жидкости. Практически невозможно осуществить падение шарика в безграничной среде, так как жидкость всегда находится в каком-то сосуде, имеющем стенки. Если шарик падает вдоль оси цилиндрического сосуда радиуса , то учет наличия стенок приводит к следующему выражению для коэффициента вязкости:

Наличие таких границ жидкости, как дно сосуда и верхняя поверхность жидкости, этой формулой не учитывается.

Выполнение работы и обработка результатов измерений

1. Измерить диаметр шариков с помощью микроскопа с окулярным микрометром. Для этого шарик положить на предметное стекло и поместить под микроскоп. Сфокусировав микроскоп, произвести отсчет делений окулярного микрометра.
2. Пинцетом опустить шарик в цилиндр с жидкостью как можно ближе к его оси; глаз наблюдателя должен быть при этом установлен против верхней метки на цилиндре с жидкостью. В момент прохождения шарика через эту метку пустить в ход секундомер. После этого глаз поместить против второй метки и в момент прохождения шарика через нее остановить секундомер. Опыт проделать с тремя шариками.
3. Определить скорости шариков по формуле:

где l — расстояние между двумя метками, t — время падения шарика.

4. Подставляя в формулу (8) значения , а также и , найти величину коэффициента внутреннего трения для каждого шарика.
5. Результаты измерений и вычислений занести в таблицу.

6. Определить среднее значение для коэффициента внутреннего трения.
7. Оценить доверительный интервал среднего результата по формуле (для доверительной вероятности 0,95):

8. Окончательный результат представить в виде:

1. Что такое вязкость? В каких единицах измеряется коэффициент вязкости?
2. Какие силы действуют на шарик, падающий в жидкости?
3. Сформулируйте закон Стокса.
4. Почему, начиная с некоторого момента времени шарик, начинает двигаться равномерно?
5. Как изменяется скорость движения шарика с увеличением его диаметра?