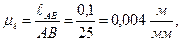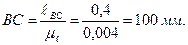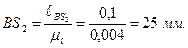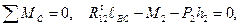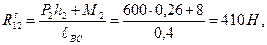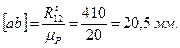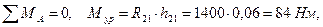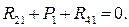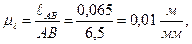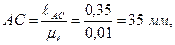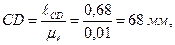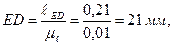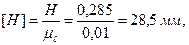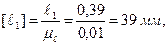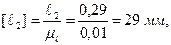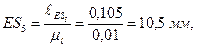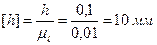Уравнение равновесия сил и многоугольник сил при силовом расчете кривошипно ползунного механизма (5 видео)

Силовой расчет кривошипно-ползунного механизма

Рассмотрим силовой расчет кривошипно-ползунного механизма компрессора.

Исходными данными являются:

1) кинематическая схема механизма;
2) массы и моменты инерции звеньев, положение их центров масс (m_vJ_xs, m_vJ_2S, т_ъ);
3) угловая скорость co_t и угловое ускорение г_] звена 1
4) сила сопротивления, приложенная к поршню F₃;
5) силы тяжести всех звеньев.

Установим последовательность выполнения силового расчета.

Для рассматриваемого положения механизма записываем векторные уравнения скоростей и ускорений, строим планы скоростей (а) и ускорений (б) (рис. 9.4). Далее определяем значения главных векторов сил инерции (Ф , Ф )

и главных моментов сил инерции (М_ф^ М _{т :}

После определения F x решаем векторное уравнение (9.5′) 21

Задавшись масштабом ц строим план сил

(рис. 9.7) для уравнения (9.5′).

Определяем угловую координату ф_2| силы F._n, замерив ее от положительного направления оси х.

Рассмотрим равновесие звена 3 (рис. 9.8).

Из условия равновесия звена 3 определяем

После этого рассматриваем равновесие кривошипа (рис. 9.9) и определяем силу F_u (рис. 9.10), угловую координату ср_м и момент М_дУ

Содержание

Примеры на силовой расчет механизма.
КИНЕТОСТАТИЧЕСКИЙ РАСЧЕТ КРИВОШИПНО-ПОЛЗУННОГО МЕХАНИЗМА, УРАВНОВЕШЕННОГО СТАТИЧЕСКИ
Методические указания к выполнению курсового проекта
📽️ Видео

Видео:Техническая механика/ Определение равнодействующей. Плоская система сходящихся сил.Скачать

Примеры на силовой расчет механизма.

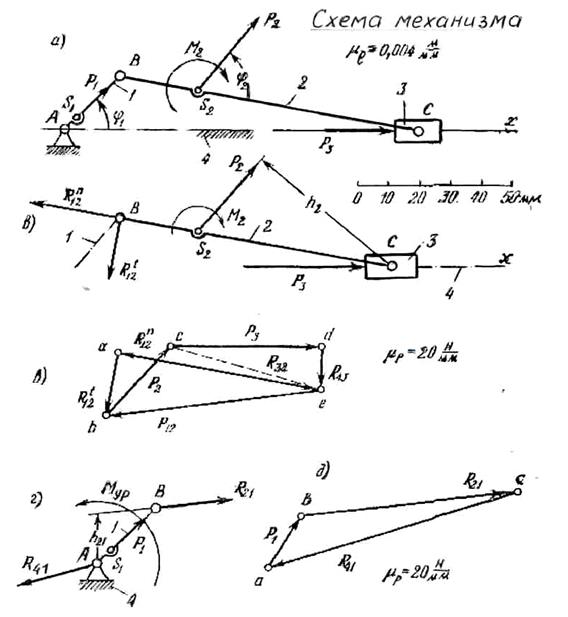
Пример 1. Провести силовой (статический) расчет кривошипно-ползунного механизма компрессора (рисунок 3.11), данного в положении, когда угол φ₁= 45 о . Исходные данные. Длины звеньев в м: ℓ_АВ = 0,1, ℓ_ВС = 0,4. Нагрузка на звенья механизма: к звену АВ в точке S₁ приложена сила Р₁=400 Н, она направлена вдоль звена АВ, расстояние ℓ_А_S₁ = 0,02 м; к звену ВС приложена сила Р₂=600 Н, она направлена под углом φ₂=60 о к линии ВС и приложена к точке S₂; расстояние ℓ_В_S₂ = 0,1 м. К этому же звену приложен момент М₂=8 Нм; к звену 3 приложена сила Р₃=1000 Н, она направлена параллельно линии Ах и линия ее действия проходит через точку С. Уравновешивающий момент М_ур приложен к звену 1.

Определить. Реакцию R₄₃ (Н) в поступательной кинематической паре С, которая направлена перпендикулярно линии Ах и проходит через точку С; реакцию R₂₃ (Н) во вращательной кинематической паре С; реакцию R₁₂ (Н) во вращательной кинематической паре В; реакцию R₄₁ (Н) во вращательной кинематической паре А и уравновешивающий момент М_ур (Нм), приложенный к звену 1.

Решение. 1). Вычерчиваем механизм в масштабе μ_ℓ

Построение механизма рассмотрено в п.2.1, §4, Примеры 1, 4.

Рассчитываем расстояния до точек приложения сил

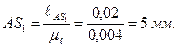
и прикладываем силы согласно заданию.

Так как расчет является статическим, то планы скоростей и ускорений строить не надо (рисунок 3.11, а).

2). Все внешние силы, действующие на звенья механизма, заданы. Поэтому и этот этап расчета выполнен.

3). Уравновешивающий момент М_ур по условию приложен к звену 1, поэтому ведущим звеном следует считать звено 1.

4). От механизма может быть отделена только одна группа Ассура, состоящая из звеньев 2 и 3. Эта группа относится ко второму классу второму виду (рисунок 3.11, б).

5). Силовой расчет структурной группы 2-3. Изображаем структурную группу 2-3 в масштабе μ_ℓ и в том же положении, что и построенная схема механизма. Составляем уравнение равновесия по первому уравнению из системы (3.17)

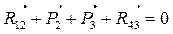
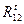
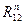
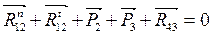
В этом уравнении содержится три неизвестные: величина и направление реакции R₁₂ и величина реакции R₄₃. Для того чтобы его решить, т.е. построить план сил группы, необходимо реакцию R₁₂ разложить на две составляющие: на тангенциальную реакцию , направленную перпендикулярно звену ВС; и на нормальную реакцию , направленную параллельно линии ВС. Тогда уравнение равновесия примет вид

(3.19)

Величину реакции 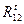определим из уравнения равновесия по второму уравнению системы (3.17)

Построение плана сил проводится по уравнению (3.19) в масштабе μ_Р=20 Н/мм. На свободном поле чертежа отмечаем точку а и от нее откладываем реакцию 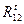в виде отрезка [аb]

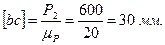
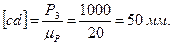
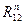
От точки b откладываем силу Р₂ в виде отрезка Далее от точки с откладываем силу Р₃ в виде отрезка Через точку а проводим прямую, параллельную звену ВС. Это будет линия действия силы . Через точку d проводим прямую, перпендикулярную линии Ах – линия действия реакции R₄₃. Точка е – пересечение этих прямых.

Отрезок [ае] в масштабе μ_Р дает искомую реакцию 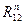, отрезок [dе] – реакцию R₄₃, а отрезок [bе] – реакцию R₁₂. Действительные величины этих реакции определяться

Для нахождения реакции R₃₂ составим уравнение равновесия звена 2

(3.20)

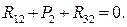
Из плана сил (рисунок 3.11, в) видно, что отрезок [се] в масштабе μ_Р дает искомую реакцию R₃₂.

Реакция R₄₃ должна проходить через точку С, т.к. к ползуну 3 приложены три силы, две из которых (R₃₂ и Р₃) проходят через эту точку.

Рисунок 3.11. – Силовой расчет кривошипно-ползунного

6). Силовой расчет ведущего звена. Изображаем ведущее звено (механизм I класса) в масштабе μ_ℓ и в том же положении, что и построенная схема механизма. К звену 1 приложены: сила Р₁=400 Н; реакция R₁₂=- R₂₁, реакция R₄₁ и уравновешивающий момент М_ур.

Составим уравнение равновесия, из которого определим величину уравновешивающего момента

где плечо h₂₁ определится по чертежу (рисунок 3.11, г)

Реакцию R₄₁ определим, составив уравнение равновесия ведущего звена

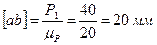
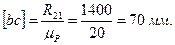
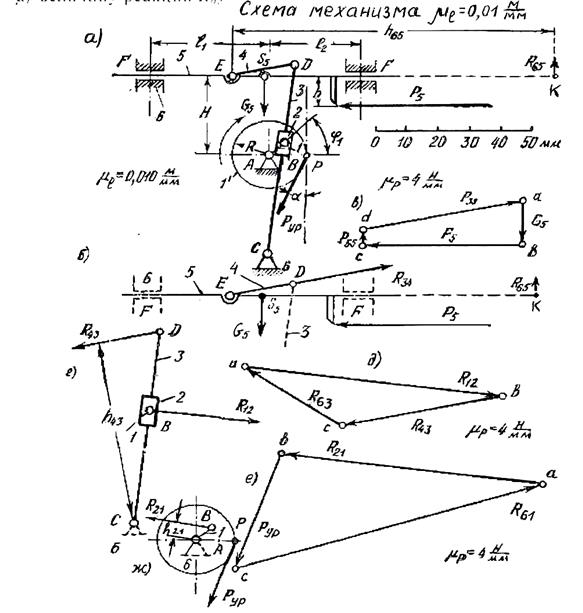
Из произвольно выбранной точки а откладываем отрезок . Из точки b откладываем отрезок Замыкающий вектор даст величину и покажет направление реакции R₄₁ (рисунок 3.11, д)

Пример 2. Провести силовой расчет шестизвенного механизма поперечно-строгального станка (рисунок 3.12, а), данного в положении, когда угол φ₁= 45 о . Исходные данные. Длины звеньев в м: ℓ_АВ = 0,065, ℓ_АС = 0,35, ℓ_С_D = 0,68, ℓ_ED = 0,21, H=0,285, ℓ₁ = 0,39, ℓ₂ = 0,29, ℓ_ES₅ = 0,105, h=0,1. Нагрузка на звенья механизма: к звену 5 приложена сила резания Р₅=200 Н; в точке S₅ звена 5 приложена сила тяжести G₅=60 H, она направлена вертикально вниз; к зубу колеса 1 ‘ , находящегося на звене 1, приложена в полюсе зацепления Р уравновешивающая сила Р_ур; радиус начальной окружности колеса 1 ‘ равен R=120 мм, угол зацепления α=20 о .

Определить. Реакции (Н) во всех кинематических парах и уравновешивающую силу Р_ур (Н), приложенную к звену 1, пренебрегая трением в кинематических парах.

Решение. 1) Строим схему механизма в масштабе μ_ℓ

Построение механизма рассмотрено в п.2.1, §4, Примеры 1, 4.

Рассчитываем расстояния до точек приложения сил G₅ и Р₅

и прикладываем силы согласно заданию.

2) Все внешние силы, приложенные к звеньям механизма, заданы, поэтому этот пункт расчета выполнен.

3) Уравновешивающая сила Р_ур приложена к звену 1, поэтому ведущим звеном следует считать звено 1 (АВ – кривошип).

4) От механизма последовательно могут быть отделены две группы II класса: группа Ассура 2 вида, состоящая из звеньев 5 и 4; и группа Ассура 3 вида, состоящая из звеньев 3 и 2.

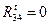
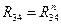
5) Силовое исследование группы Ассура 4-5 (рисунок 3.12, б). Действуют внешние силы G₅, Р₅, реакции R₃₄ и R₆₅. Реакция R₃₄ приложена к центру шарнира D и направлена вдоль звена ED, т.к. звено 4 не нагружено внешними силами и тангенциальная составляющая . Поэтому, . Реакция R₆₅ направлена перпендикулярно направляющим звена 5, точка приложения её неизвестна (условно точка приложения – точка К).

Составим уравнение равновесия всей структурной группы

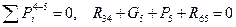
Строим план сил (рисунок 3.12, в). Выбираем масштаб сил μ_Р=4Н/мм. От точки а откладываем силу G₅ в виде отрезка [ab]

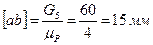
Далее от точки b откладываем силу Р₅ в виде отрезка

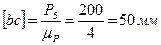
Через точку а проводим линию, параллельную ED (направление линии действия реакции R₃₄), а через точку с – линию, параллельную направляющим звена 5 (направление линии действия реакции R₆₅), до их взаимного пересечения в точке d. Отрезок [сd] дает в масштабе μ_Р величину реакции R₆₅

Отрезок [dа] дает величину реакции R₃₄

Точку К приложения реакции R₆₅ найдем из условия равновесия звена 5

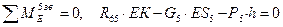
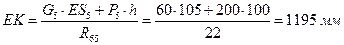
Рисунок 3.12. – Силовой расчет механизма

5) Силовое исследование группы Ассура 2-3 (рисунок 3.12, г). Внешние силы отсутствуют. Реакция R₄₃приложена к точке D и направлена в противоположную сторону реакции R₃₄. Реакция R₁₂направлена перпендикулярно звену CD. Определим реакцию R₁₂ из уравнения моментов относительно точки С

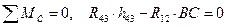
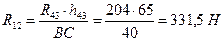
Составляем уравнение равновесия группы Ассура 2-3

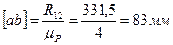
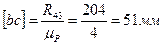
Строим план сил в масштабе μ_Р=4 Н/мм (рисунок 3.12, д). Из произвольно выбранной точки а откладываем реакцию R₁₂ в виде отрезка перпендикулярно звену CD. Далее от точки b откладываем реакцию R₄₃ в виде отрезка . Соединяя точки с и а прямой, получаем величину и направление реакции R₆₃ = [са] μ_Р = 38·4 = 152 Н.

6) Силовой расчет ведущего звена (рисунок 3.12, ж). Передача крутящего момента осуществляется через зубчатую передачу. К звену 1 приложены силы: реакция R₂₁ = -R₁₂, реакция в шарнире А (равная R₆₁) и уравновешивающая сила Р_ур, приложенная в точке Р колеса 1′ под углом α к касательной, проведенной к начальной окружности.

Составим уравнение моментов звена 1 (АВ)

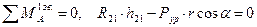
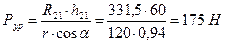
Составляем уравнение равновесия ведущего звена

Строим план сил ведущего звена в масштабе μ_Р=4 Н/мм (рисунок 3.12, е). Из произвольно выбранной точки а откладываем реакцию R₂₁ в виде отрезка 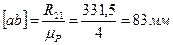перпендикулярно звену CD. Далее от точки b откладываем реакцию Р_ур в виде отрезка . Соединяя точки с и а прямой, получаем величину и направление реакции R₆₁ = [са] μ_Р = 102·4 = 408 Н.

Дата добавления: 2015-06-01 ; просмотров: 4838 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Силовой анализ кривошипно-ползунного механизмаСкачать

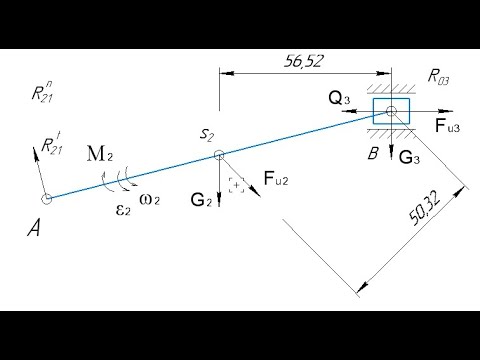
КИНЕТОСТАТИЧЕСКИЙ РАСЧЕТ КРИВОШИПНО-ПОЛЗУННОГО МЕХАНИЗМА, УРАВНОВЕШЕННОГО СТАТИЧЕСКИ

На рис. 4.5, а показана кинематическая схема четырехзвенного криво- шипно-ползунного механизма, для частичного статического уравновешивания которого на кривошипе установлен противовес 4 массой т_п. Его статический момент вычисляется по формуле (4.9). Противовес не влияет на систему сил, действующих на структурную группу, в частности на величину и направление реакций R_n, R₀₃, R₂₃ (или R₃₂). Схема нагружения структурной группы приведена на рис. 4.5, б.

В соответствии с формулой (3.21) силы тяжести шатуна и ползуна: В соответствии с формулами (3.1) и (3.2) силы инерции звеньев:

Условие равновесия системы сил, действующих на шатун:

где h h₂ натуральные плечи сил G₂ и Р_И2 соответственно.

Реакция R T _n определяется при решении уравнения (4.10). Силы R»₂ и /?₀₃ определяются при решении векторного уравнения

Графическое решение уравнения (4.11) показано на рис. 4.5, в. План сил построен в масштабе (л_р.

Схема нагружения кривошипа показана на рис. 4.6, а. Противовес рассматривается как точечная масса. Силы тяжести кривошипа и противовеса:

Силы инерции кривошипа и противовеса: где ас — ускорение точки С кривошипа.

Уравнения равновесия кривошипа:

По уравнению (4.12) вычисляется уравновешивающий момент, а по уравнению (4.13) — реакция /?₀₁. Графическое решение уравнения (4.13) приведено на рис. 4.6, б. R_0l -af • /л_Р. Если бы механизм не был уравновешен, реакция R’_0] в шарнире О на плане сил (рис. 4.6, б) изображалась бы отрезком ad. Rq _{= ad ? ju_p.} Расчет показал, что после установки противовеса на кривошип величина реакции R_0] уменьшилась.

Видео:ПРАКТИКА# 9. ТММ. ПРИМЕР И ПОСТРОЕНИЕ.Скачать

Методические указания к выполнению курсового проекта

Задания на курсовой проект (КП) содержатся в приложениях 2-4. Они отличаются уровнем сложности кинематических схем механизмов и набором задач, которые должны быть решены студентом в ходе курсового проектирования.

Так, при выполнении задания типа С4 (прил. 2) студент должен провести метрический синтез четырехзвенного кривошипно-ползунного механизма, его структурный, кинематический, силовой расчет и частичное статическое уравновешивание.

В заданиях типа У4 (прил. 4) кинематические размеры кривошипно- ползунного механизма заданы. В ходе курсового проектирования обучающийся решает задачи структурного, кинематического и силового анализа. По желанию для увеличения рейтинга он может выполнить частичное статическое уравновешивание с последующим силовым расчетом уравновешенного механизма.

Наиболее сложные задания на КП содержатся в приложении 3 (задания с номерами 6-1-6-18). Они предусматривают структурный, кинематический и кинетостатический анализ сложного шестизвенного рычажного механизма, содержащего структурные группы II класса 2-го порядка разных видов.

Независимо от сложности задания целесообразно придерживаться следующего алгоритма выполнения КП.

1. Изучаются исходные данные, и в случае отсутствия кинематических размеров производится метрический синтез механизма (подраздел 2.2 данного учебного пособия).
2. Выполняется структурный анализ механизма, результат которого используется на последующих этапах расчета.
3. В соответствии с формулой строения механизма методом планов выполняется его кинематический расчет:
— в масштабе строится разметка механизма для 12 положений и определяются его крайние положения (подраздел 2.3 учебного пособия);
— для 12 положений механизма методом планов определяются линейные и угловые скорости звеньев и отдельных их точек, в частности центров масс. Расчетные модели описаны в подразделе 2.1, пример их использования — в подразделах 2.3 и 3.4;
— для двух положений механизма (по согласованию с преподавателем) выполняется расчет ускорений, соответствующие расчетные модели описаны в подразделах 2.1, 2.3 и 3.4.
4. Кинетостатический расчет механизма методом планов выполняется для двух его положений. Расчетные модели структурных групп и исходного механизма, последовательность расчета приведены в подразделах 3.2-3.4 учебного пособия. Метод определения сил инерции (подраздел 3.1) согласуется с преподавателем.
5. Уравновешивающий момент М_ур вычисляется методом Н. Е. Жуковского для двух положений механизма. Методика расчета приведена в подразделе 3.5. На этом этапе выполнения КП оценивается (в процентах) расхождение результатов расчета М_ур, полученных разными методами.
6. Определяются параметры противовеса, устанавливаемого в плоскости движения кривошипа, и для двух положений методом планов выполняется силовой расчет уравновешенного механизма (подраздел 4.2).

При исследовании сложного рычажного механизма (прил. 3) пункты 1 и 6 данного алгоритма не выполняются.

Пояснительная записка формируется параллельно с выполнением расчетов. Требования к ее оформлению будут сформулированы в следующем разделе данного учебного пособия.