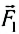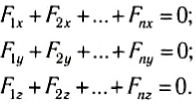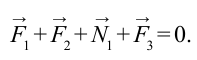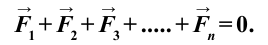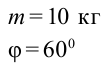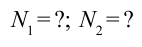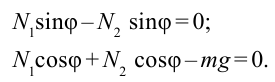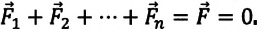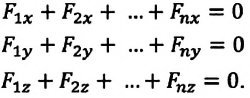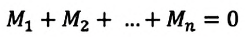Уравнение равновесия при вращательном движении (7 видео)

Вращение твердого тела

Для кинематического описания процесса вращения твердого тела нужно ввести такие понятия как угловое перемещение Δ φ , угловое ускорение ε и угловая скорость ω :

ω = ∆ φ ∆ t , ( ∆ t → 0 ) , ε = ∆ φ ∆ t , ( ∆ t → 0 ) .

Углы выражаются в радианах. За положительное направление вращения принимается направление против часовой стрелки.

Когда твердое тело вращается относительно неподвижной оси, все точки этого тела перемещаются с одинаковыми угловыми скоростями и ускорениями.

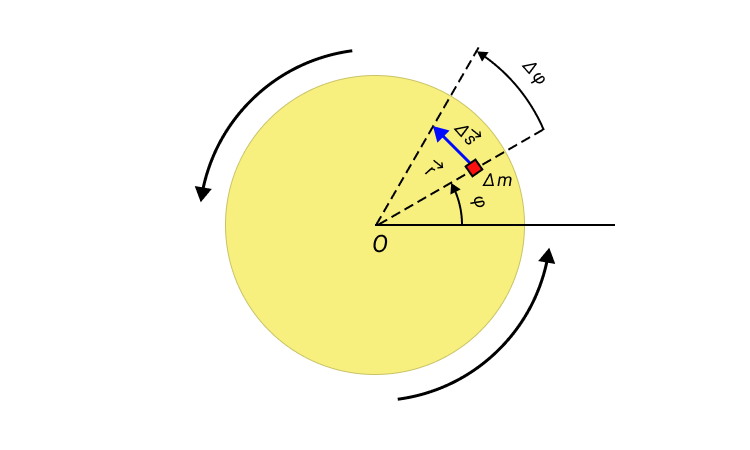
Рисунок 1. Вращение диска относительно оси, проходящей через его центр O .

Если угловое перемещение Δ φ мало, то модуль вектора линейного перемещения ∆ s → некоторого элемента массы Δ m вращающегося твердого тела можно выразить соотношением:

в котором r – модуль радиус-вектора r → .

Между модулями угловой и линейной скоростей можно установить связь посредством равенства

Модули линейного и углового ускорения также взаимосвязаны:

Векторы v → и a → = a τ → направлены по касательной к окружности радиуса r .

Также нам необходимо учесть возникновение нормального или центростремительного ускорения, которое всегда возникает при движении тел по окружности.

Модуль ускорения выражается формулой:

a n = v 2 r = ω 2 r .

Если разделить вращающееся тело на небольшие фрагменты Δ m i , обозначить расстояние до оси вращения через r i , а модули линейных скоростей через v i , то запись формулы кинестетической энергии вращающегося тела будет иметь вид:

E k = ∑ i ν m v i 2 2 = ∑ i ∆ m ( r i ω ) 2 2 = ω 2 2 ∑ i ∆ m i r i 2 .

Физическая величина ∑ i ∆ m i r i 2 носит название момента инерции I тела относительно оси вращения. Она зависит от распределения масс вращающегося тела относительно оси вращения:

I = ∑ i ∆ m i r i 2 .

В пределе при Δ m → 0 эта сумма переходит в интеграл. Единица измерения момента инерции в С И – килограмм—метр в квадрате ( к г · м 2 ) . Таким образом, кинетическую энергию твердого тела, вращающегося относительно неподвижной оси, можно представить в виде:

В отличие от выражения, которое мы использовали для описания кинестетической энергии поступательно движущегося тела m v 2 2 , вместо массы m в формулу входит момент инерции I . Также мы принимаем во внимание вместо линейной скорости v угловую скорость ω .

Если для динамики поступательного движения основную роль играет масса тела, то в динамике вращательного движения имеет значение момент инерции. Но если масса – это свойство рассматриваемого твердого тела, которое не зависит от скорости движения и других факторов, то момент инерции зависит от того, вокруг какой оси вращается тело. Для одного и того же тела момент инерции будет определяться различными осями вращения.

В большинстве задач считается, что ось вращения твердого тела проходит через центр его массы.

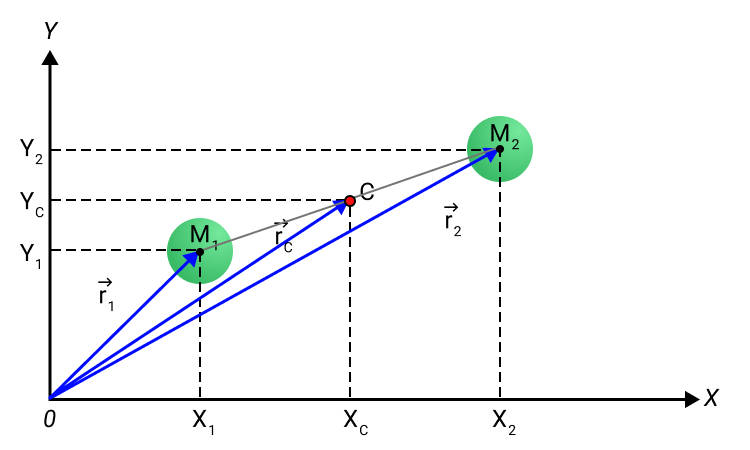
Положение x C , y C центра масс для простого случая системы из двух частиц с массами m 1 и m 2 , расположенными в плоскости X Y в точках с координатами x 1 , y 1 и x 2 , y 2 определяется выражениями:

x C = m 1 x 1 + m 2 x 2 m 1 + m 2 , y C = m 1 y 1 + m 2 y 2 m 1 + m 2 .

Рисунок 2. Центр масс C системы из двух частиц.

В векторной форме это соотношение принимает вид:

r C → = m 1 r 1 → + m 2 r 2 → m 1 + m 2 .

Аналогично, для системы из многих частиц радиус-вектор r C → центра масс определяется выражением

r C → = ∑ m i r i → ∑ m i .

Если мы имеем дело с твердым телом, состоящим из одной части, то в приведенном выражении суммы для r C → необходимо заменить интегралами.

Центр масс в однородном поле тяготения совпадает с центром тяжести. Это значит, что если мы возьмем тело сложной формы и подвесим его за центр масс, то в однородном поле тяготения это тело будет находиться в равновесии. Отсюда следует способ определения центра масс сложного тела на практике: его необходимо последовательно подвесить за несколько точек, одновременно отмечая по отвесу вертикальные линии.

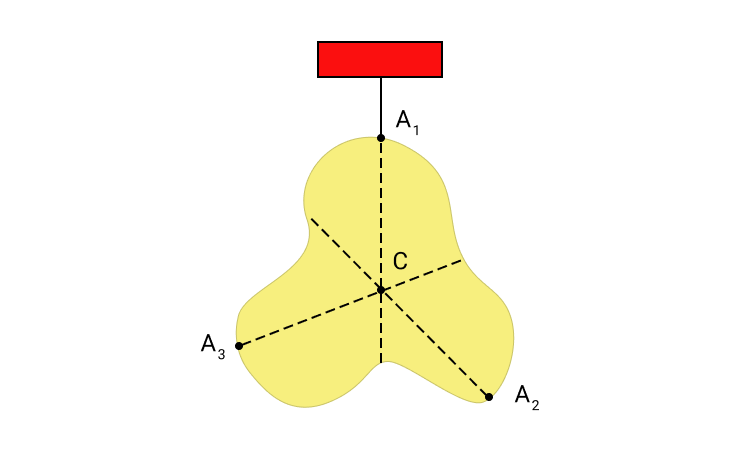
Рисунок 3. Определение положения центра масс C тела сложной формы. A 1 , A 2 , A 3 точки подвеса.

На рисунке мы видим тело, которое подвешено за центр масс. Оно находится в состоянии безразличного равновесия. В однородном поле тяготения равнодействующая сил тяжести приложена к центру масс.

Мы можем представить любое движение твердого тела как сумму двух движений. Первое поступательное, которое производится со скоростью центра масс тела. Второе – это вращение относительно оси, которая проходит через центр масс.

Предположим. Что у нас есть колесо, которое катится по горизонтальной поверхности без проскальзывания. Все точки колеса во время движения перемещаются параллельно одной плоскости. Такое движение мы можем обозначить как плоское.

Содержание

Теорема о движении центра масс
Теорема Штейнера о параллельном переносе оси вращения
Основное уравнение динамики вращательного движения твердого тела
Закон сохранения момента импульса
Условие равновесного состояния при вращательном движении
Условия равновесия тел в физике — формулы и определение с примерами
Условия равновесия тел
Виды равновесия
Устойчивое равновесие
Неустойчивое равновесие
Безразличное равновесие
Образец решения задачи
Определение условия равновесия тела
Равновесие тела при поступательном движении
Равновесие тела с неподвижной осью вращения
🎬 Видео

Видео:Статика. Момент сил. Условия равновесия тел | Физика ЕГЭ, ЦТ, ЦЭ | Физика для школьниковСкачать

Теорема о движении центра масс

Кинестетическая энергия вращающегося твердого тела при плоском движении будет равна сумме кинетической энергии поступательного движения и кинетической энергии вращения относительно оси, которая проведена через центр масс и располагается перпендикулярно плоскостям, в которых движутся все точки тела:

E k = m v C 2 2 + I C ω 2 2 ,

где m – полная масса тела, I C – момент инерции тела относительно оси, проходящей через центр масс.

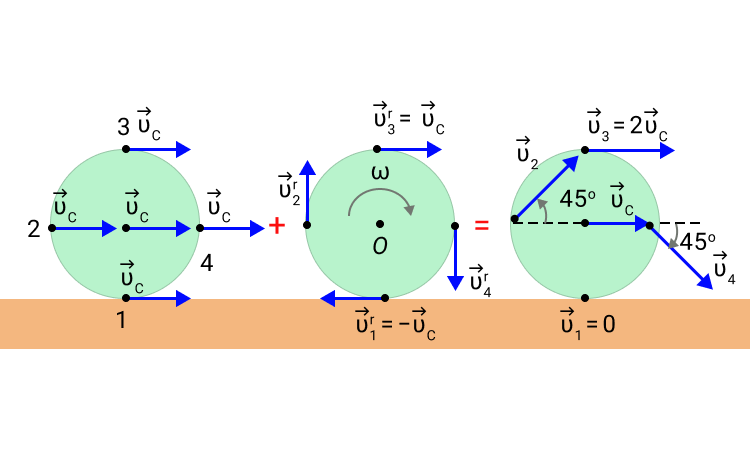
Рисунок 4. Качение колеса как сумма поступательного движения со скоростью v C → и вращения с угловой скоростью ω = v C R относительно оси O , проходящей через центр масс.

В механике используется теорема о движении центра масс.

Любое тело или несколько взаимодействующих тел, которые представляют собой единую систему, обладают центром масс. Этот центр масс под воздействием внешних сил перемещается в пространстве как материальная точка, в которой сосредоточена вся масса системы.

На рисунке мы изобразили движение твердого тела, на которое действуют силы тяжести. Центр масс тела движется по траектории, которая близка к параболе, тогда как траектория остальных точек тела является более сложной.

Рисунок 5. Движение твердого тела под действием силы тяжести.

Видео:Урок 70. Виды равновесия. Условие равновесия тела при отсутствии вращения.Скачать

Теорема Штейнера о параллельном переносе оси вращения

Рассмотрим случай, когда твердое тело движется вокруг некоторой неподвижной оси. Момент инерции этого тела инерции I можно выразить через момент инерции I C этого тела относительно оси, проходящей через центр масс тела и параллельной первой.

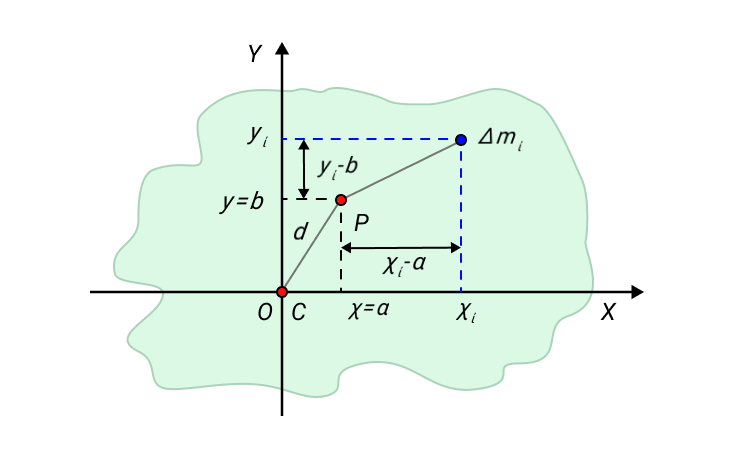
Рисунок 6. К доказательству теоремы о параллельном переносе оси вращения.

Для примера возьмем твердое тело, форма которого произвольна. Обозначим центр масс С . Выберем систему координат Х У с началом координат 0 . Совместим центр масс и начало координат.

Одна из осей проходит через центр масс С . Вторая ось пересекает произвольно выбранную точку Р , которая расположена на расстоянии d от начала координат. Выделим некоторый малый элемент массы данного твердого тела Δ m i .

По определению момента инерции:

I C = ∑ ∆ m i ( x i 2 + y i 2 ) , I P = ∑ m i ( x i — a ) 2 + y i — b 2

Выражение для I P можно переписать в виде:

I P = ∑ ∆ m i ( x i 2 + y i 2 ) + ∑ ∆ m i ( a 2 + b 2 ) — 2 a ∑ ∆ m i x i — 2 b ∑ ∆ m i y i .

Два последних члена уравнения обращаются в нуль, так как начало координат в нашем случае совпадает с центром масс тела.

Так мы пришли к формуле теоремы Штейнера о параллельном переносе оси вращения.

Для тела, которое вращается относительно произвольной неподвижной оси, момент инерции, согласно теореме Штейнера, равен сумме момента инерции этого тела относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями.

I P = I C + m d 2 ,

где m – полная масса тела.

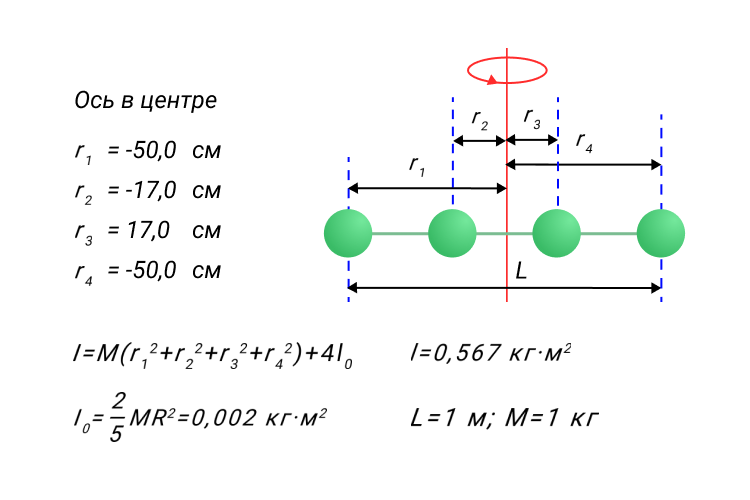
Рисунок 7. Модель момента инерции.

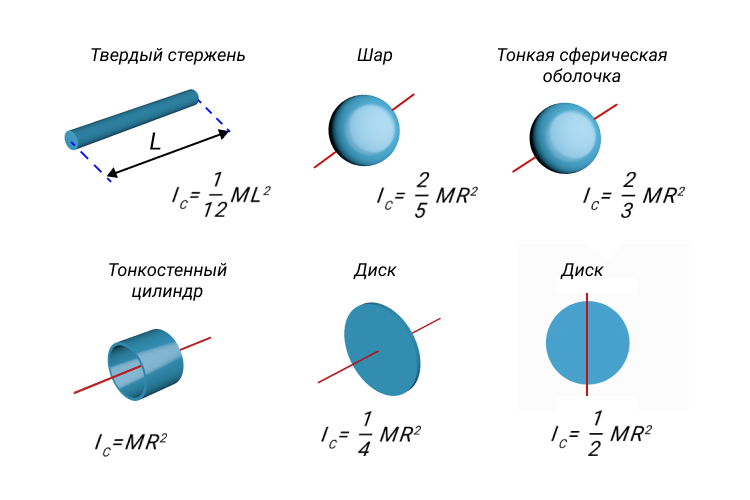
На рисунке ниже изображены однородные твердые тела различной формы и указаны моменты инерции этих тел относительно оси, проходящей через центр масс.

Рисунок 8. Моменты инерции I C некоторых однородных твердых тел.

Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

Основное уравнение динамики вращательного движения твердого тела

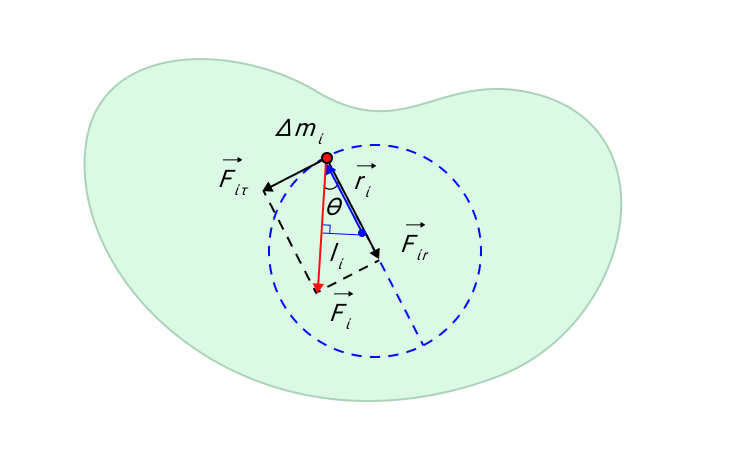
В тех случаях, когда мы имеем дело с твердым телом, которое вращается относительно неподвижной оси, мы можем обобщить второй закон Ньютона. На рисунке ниже мы изобразили твердое тело произвольной формы, вращающееся относительно некоторой оси, проходящей через точку О . Ось вращения расположена перпендикулярно плоскости рисунка.

Δ m i – это произвольный малый элемент массы, на который оказывают воздействие внешние и внутренние силы. Равнодействующая всех сил есть F i → . Ее можно разложить на две составляющие: касательную составляющую F i τ → и радиальную F i r → . Радиальная составляющая F i r → создает центростремительное ускорение a n .

Рисунок 9. Касательная F i τ → и радиальная F i r → составляющие силы F i → действующей на элемент Δ m i твердого тела.

Касательная составляющая F i τ → вызывает тангенциальное ускорение a i τ → массы Δ m i . Второй закон Ньютона, записанный в скалярной форме, дает

∆ m i a i τ = F i τ sin θ или ∆ m i r i ε = F i sin θ ,

где ε = a i τ r i – угловое ускорение всех точек твердого тела.

Если обе части написанного выше уравнения умножить на r i , то мы получим:

∆ m i r i 2 ε = F i r i sin θ = F i l i = M i .

Здесь l i – плечо силы, F i , → M i – момент силы.

Теперь нужно аналогичные соотношения записать для всех элементов массы Δm_i вращающегося твердого тела, а затем просуммировать левые и правые части. Это дает:

∑ ∆ m i r i 2 ε = ∑ M i .

Стоящая в правой части сумма моментов сил, действующих на различные точки твердого тела, состоит из суммы моментов всех внешних сил и суммы моментов всех внутренних сил.

∑ M = ∑ M i в н е ш н + ∑ M i в н у т р .

Но сумма моментов всех внутренних сил согласно третьему закону Ньютона равна нулю, поэтому в правой части остается только сумма моментов всех внешних сил, которые мы будем обозначать через M . Так мы получили основное уравнение динамики вращательного движения твердого тела.

Угловое ускорение ε и момент сил M в этом уравнении являются величинами алгебраическими.

Обычно за положительное направление вращения принимают направление против часовой стрелки.

Возможна и векторная форма записи основного уравнения динамики вращательного движения, при которой величины ω → , ε → , M → определяются как векторы, направленные по оси вращения.

Видео:Вращательное движение. 10 класс.Скачать

Закон сохранения момента импульса

В разделе, посвященном поступательному движению тела, мы ввели понятие импульса тела p → . По аналогии с поступательным движением для вращательного движения мы вводим понятие момента импульса.

Момент импульса вращающегося тела – это физическая величина, которая равняется произведению момента инерции тела I на угловую скорость ω его вращения.

Для обозначения момента импульса используется латинская буква L .

Поскольку ε = ∆ ω ∆ t ; ∆ t → 0 , уравнение вращательного движения можно представить в виде:

M = I ε = I ∆ ω ∆ t или M ∆ t = I ∆ ω = ∆ L .

M = ∆ L ∆ t ; ( ∆ t → 0 ) .

Мы получили это уравнение для случая, когда I = c o n s t . Но оно будет справедливо и тогда, когда момент инерции тела будет изменяться в процессе движения.

Если суммарный момент M внешних сил, действующих на тело, равен нулю, то момент импульса L = I ω относительно данной оси сохраняется: ∆ L = 0 , если M = 0 .

L = l ω = c o n s t .

Так мы пришли к закону сохранения момента импульса.

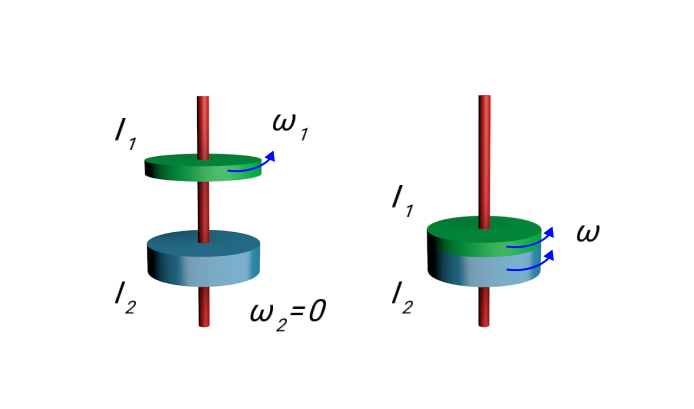
В качестве примера приведем рисунок, на котором изображено неупругое вращательное столкновение дисков, которые насажены на общую для них ось.

Рисунок 10. Неупругое вращательное столкновение двух дисков. Закон сохранения момента импульса: I 1 ω 1 = ( I 1 + I 2 ) ω .

Мы имеем дело с замкнутой системой. Для любой замкнутой системы закон сохранения момента импульса будет справедливым. Он выполняется и в условиях экспериментов по механике, и в условиях космоса, когда планеты движутся по своим орбитам вокруг звезды.

Мы можем записать уравнение динамики вращательного движения как для неподвижной оси, так и для оси, которая перемещается равномерно или с ускорением. Вид уравнения не изменится и в том случае, если ось движется ускоренно. Для этого должно выполняться два условия: ось должна проходить через центр массы тела, а ее направление в пространстве остается неизменным.

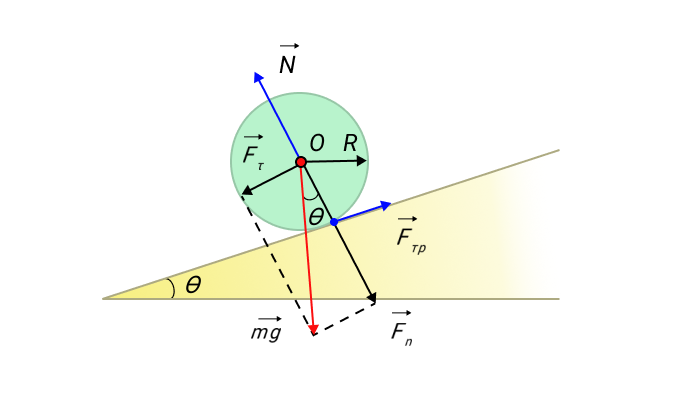
Предположим, что у нас есть тело (шар или цилиндр), которое катится по наклонной плоскости с некоторым трением.

Рисунок 11. Качение симметричного тела по наклонной плоскости.

Ось вращения O проходит через центр масс тела. Моменты силы тяжести m g → и силы реакции N → относительно оси O равны нулю. Момент M создает только сила трения: M = F т р R .

Уравнение вращательного движения:

I C ε = I C a R = M = F т р R ,

где ε – угловое ускорение катящегося тела, a – линейное ускорение его центра масс, I C – момент инерции относительно оси O , проходящей через центр масс.

Второй закон Ньютона для поступательного движения центра масс записывается в виде:

m a = m g sin α — F т р .

Исключая из этих уравнений F т р , получим окончательно:

α = m g sin θ I C R 2 + m .

Из этого выражения видно, что быстрее будет скатываться с наклонной плоскости тело, обладающее меньшим моментом инерции. Например, у шара I C = 2 5 m R 2 , а у сплошного однородного цилиндра I C = 1 2 m R 2 . Следовательно, шар будет скатываться быстрее цилиндра.

Видео:Физика 10 класс (Урок№5 - Поступательное движение. Вращательное движение твердого тела.)Скачать

Условие равновесного состояния при вращательном движении

В физике под равновесным состоянием тела подразумевается, что оно не испытывает никакого ускорения (находится в покое или движется с постоянной скоростью).

Условие равновесия для поступательного движения означает, что сумма всех сил, действующих на тело, равна нулю: ΣF=0.

Условие равновесия для вращательного движения означает, что сумма всех моментов сил, действующих на тело, равна нулю: ΣМ=0.

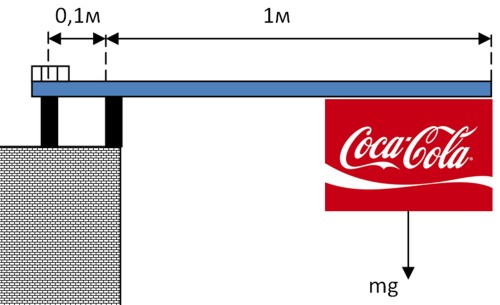
Используя полученные знания, произведем расчет прочности болта, который должен удерживать рекламную вывеску у магазина, как изображено на рисунке ниже.

Масса плаката — 10 кг;
Длина шеста, на котором крепится плакат, от точки опоры — 1 м;
Расстояние от крепежного болта до точки опоры — 0,1 м;
Массу шеста учитывать не будем.

Для того, чтобы плакат висел, необходимо, чтобы выполнялось условие равновесия: ΣМ=0.

М_пл — момент силы со стороны плаката;
М_б — момент силы со стороны болта.

Момент силы плаката определяем по формуле:

m — масса плаката;
g — ускорение свободного падения;
mg — сила тяжести плаката;
L_пл — плечо силы тяжести плаката.

Подставляем числовые значения в формулу:

Знак минус означает, что вектор ускорения свободного падения направлен вниз, в сторону, противоположную выбранному направлению оси координат.

Момент силы со стороны болта:

F_b — сила, с которой болт должен удерживать конструкцию (искомая величина);
L_б — плечо силы болта.

В формулу моментов сил:

Подставим соответствующие выражения для моментов сил плаката и болта:

Выполнив несложные алгебраические преобразования, получим нужную формулу нахождения искомой силы:

Знак минус в правой части формулы говорит о том, что сила, с которой болт должен удерживать конструкцию, направлена в противоположную сторону вектора свободного падения, т.е., вверх. Подставляем числовые значения в формулу:

Зная силу, с которой болт должен удерживать конструкцию, несложно подобрать болт нужных размеров по справочнику.

Если вам понравился сайт, будем благодарны за его популяризацию 🙂 Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:

Код кнопки:
Политика конфиденциальности Об авторе

Видео:Урок 125. Работа, мощность и кинетическая энергия при вращательном движенииСкачать

Условия равновесия тел в физике — формулы и определение с примерами

Содержание:

Условия равновесия тел:

Основным признаком взаимодействия тел в динамике является возникновение ускорений. Однако часто бывает нужно знать, при каких условиях тело, на которое действует несколько сил, не движется с ускорением, а покоится или движется равномерно и прямолинейно. В последнем случае мы всегда можем выбрать другую инерциальную систему отсчета, в которой тело покоится, поэтому в дальнейшем будем изучать условия равновесия покоящихся тел.

Раздел механики, в котором изучаются условия равновесия тел, называется статикой.

Все опытные факты, которые мы рассмотрели в предыдущих параграфах, убеждают нас в том, что тело покоится, если равнодействующая всех сил, действующих на него, равна нулю.

Итак, первое условие равновесия тела: векторная сумма всех сил, приложенных к телу, равна нулю.
Если на тело действует n сил

Из этого условия следует, что и сумма проекций всех сил на любое направление тоже должна быть равна нулю. В частности, сумма проекций сил на оси выбранной декартовой системы координат равна нулю:

Фактически эти три равенства эквивалентны одному векторному равенству ( 1 ). Но с их помощью достаточно просто решать задачи, поскольку проекции сил — скалярные величины.

В повседневной жизни и технике часто встречаются тела, которые не могут двигаться поступательно, но могут вращаться вокруг оси. Примерами таких тел могут служить двери и окна, качели, колеса машин и детали механизмов и т. д.

На рисунке 149, а изображен однородный диск, который может вращаться вокруг закрепленной оси, проходящей через его центр — точку О. Если подвесить к нему тело в точке А, то диск будет находиться в равновесии.

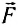
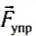
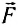
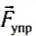
Естественно, что действующая сила будет уравновешиваться силой упругости со стороны оси вращения. Если подвесить тело в точке В, то равновесие тоже не нарушится. Отсюда можно сделать вывод, что точку приложения силы натяжения можно переносить вдоль линии действия силы. При этом силы и лежат на одной прямой.

Если же прямая, на которой лежит вектор силы 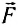, не проходит через ось вращения, то эта сила не может быть уравновешена силой упругости оси, и тело поворачивается вокруг нее (рис. 149, б).

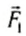
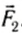
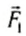
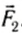
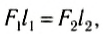
На рисунке 149, в изображен тот же диск, на который действуют две силы и . Численные значения этих сил определяются динамометрами. Сила вращает диск против часовой стрелки, а сила — по часовой стрелке. Диск не будет вращаться, если выполняется условие:
(2)

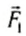
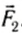
где l₁ и l₂ — кратчайшие расстояния от оси вращения до прямых, на которых лежат векторы сил и .

Итак, мы получили известное вам из курса физики 8-го класса условие равновесия рычага.

Кратчайшее расстояние от оси вращения до линии действия силы называется плечом силы, а произведение модуля силы F на плечо l называется моментом силы М:
M = Fl (3)

Из определения момента силы следует, что единицей его измерения в СИ является 1 ньютон-метр (1 H . м).

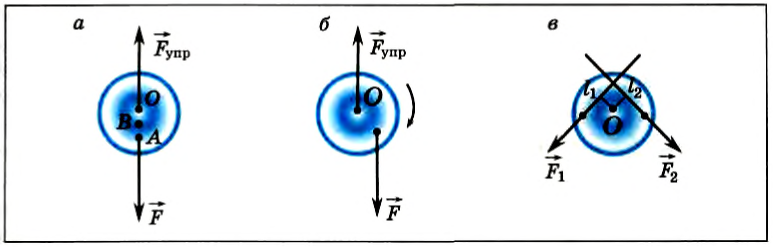
Рис. 149

Следовательно, равенство (2) означает равенство моментов сил F₁ и F₂. Но момент силы F₁ вращает диск против часовой стрелки, а момент силы F₂ — по часовой стрелке. Поэтому им нужно приписать различные знаки. Обычно положительным считают момент силы, вызывающий вращение по часовой стрелке, а отрицательным — момент силы, вызывающий вращение против часовой стрелки.

Если же на тело, закрепленное на оси, действуют n сил, то оно будет в равновесии, если алгебраическая сумма моментов сил будет равна нулю:
M₁+ M₂ + . +M_n = 0. (4)

Итак, вторым условием равновесия тела является правило моментов: тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех сил, приложенных к телу, относительно этой оси равна нулю.

Таким образом, тело будет находиться в равновесии, если выполняются два условия: (1) и (4). Например, доска, изображенная на рисунке 150, находится в равновесии.

Рис. 150

Главные выводы:

Чтобы тело находилось в равновесии, векторная сумма всех сил, действующих на него, должна быть равна нулю.
При равновесии тела сумма проекций всех сил, действующих на тело, на любое направление должна быть равна нулю.
Точку приложения силы можно переносить вдоль линии действия силы.
Вторым условием равновесия тела является равенство нулю алгебраической суммы моментов приложенных к телу сил.

Видео:Поступательное и вращательное движения.Скачать

Условия равновесия тел

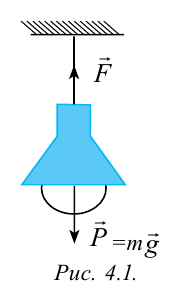
Рассмотрим силы, действующие на подвешенную к потолку лампу (рис. 4.1). Для начала вспомним изученное в 6-м классе понятие «центр масс» тела.

Центр масс – это воображаемая точка, в которой воплощена вся масса тела.
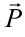
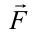
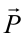
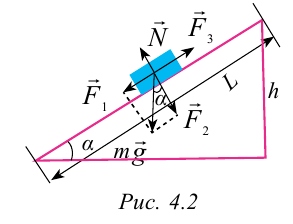
Исходя из этого будем считать, что силы, действующие на тело, приложены к центру масс. На подвешенную лампу действует направленная вниз сила тяжести . При этом туго натягивается удерживающая ее нить. Возникающая в нити сила натяжения и сила тяжести действуют вдоль одной прямой линии, которая проходит через центр массы и направлены противоположно. Эти силы равны по модулям. Если эти силы сложить по правилу сложения векторов, то результирующая сила становится равной нулю. Поэтому лампа остается в положении равновесия.

Рассмотрим случай, когда тело покоится в равновесии на наклонной плоскости (рис. 4.2). Рассмотрим действующие относительно центра масс силы в этом случае. На тело действует сила тяжести .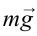
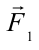
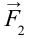
Эту силу разделим на составляющие: и .

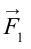
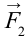
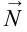
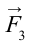
При этом сила стремится сдвинуть тело вниз по наклонной плоскости, сила представляет силу давления на площадь наклонной плоскости. Эта сила приводит к образованию силы реакции на тело со стороны наклонной плоскости. Также на тело действует сила трения в противоположном относительно скольжения направлении.

В этом случае векторная сумма всех действующих сил тоже будет равна нулю.

Исходя из вышесказанного можно сделать следующие выводы:
Для того чтобы тело или система тел, не имеющие вращения оси, остались в равновесии, векторная сумма всех действующих на них сил должна быть равна нулю.

Виды равновесия

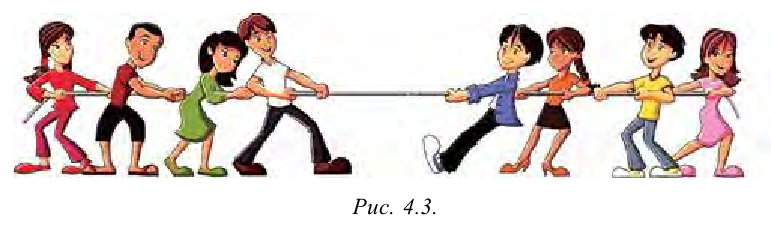
Если некое тело находится в состоянии равновесия, это не означает, что оно постоянно будет находиться в таком состоянии (рис. 4.3). В реальных условиях тело подвергается неожиданным воздействиям извне, которые невозможно избежать. Главное, что нужно знать – останется ли тело после такого воздействия в равновесии или равновесие будет нарушено. Для этого необходимо учесть направление результирующей силы внешнего воздействия. В зависимости от направления результирующей силы различают три вида равновесия.

Устойчивое равновесие

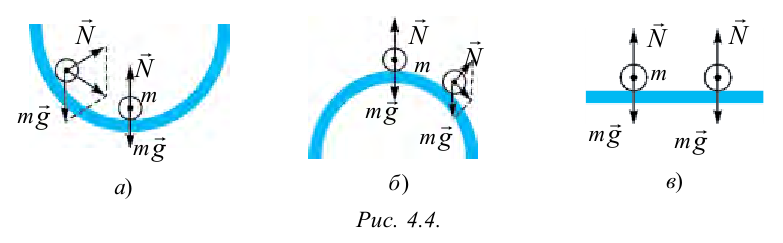
При выведении тела из положения равновесия возникают силы, возвращающие тело в прежнее положение, это называется устойчивым равновесием (рис. 4.4а). В данном случае, при небольшом смещении шарика, лежащего на дне сферического углубления, равнодействующая сила возвращает его в положение равновесия.

Неустойчивое равновесие

При выведении тела из положения равновесия возникают силы, удаляющие его от положения равновесия, это называется неустойчивым равновесием (рис. 4.4б). В данном случае шарик находится в верхней точке выпуклой сферической поверхности. При небольшом смещении из положения равновесия равнодействующая сила действующих на него сил удаляет его еще дальше от состояния равновесия.

Безразличное равновесие

Равновесие, при котором смещение тела в любом направлении не вызывает изменения действующих на него сил и равновесие тела сохраняется, называется безразличным равновесием (рисунок 4.4в). Если приложить силу к шарику, находящемуся на горизонтальной поверхности, то он переместится на другое место.

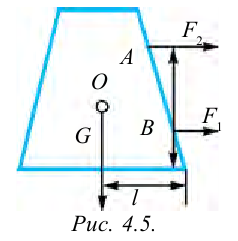
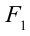
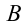
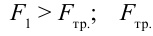
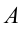
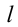
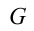
Если на тело, показанное на рисунке 4.5 действует сила в точке ниже центра тяжести ( – сила трения), тело приходит в поступательное движение. Не меняя величину силы, приложим ее к точке , при этом тело начинает наклоняться. Начинает уменьшаться расстояние между крайними точками нижнего основания контура и вектором, направленным вниз из центра тяжести. Если продолжить прикладывать силу, вектор выйдет за пределы контура тела и оно опрокинется.

Таким образом, равновесие тела зависит от:

1) веса тела;
2) величины площади основания тела;
3) места приложения сил относительно центра тяжести.

Образец решения задачи

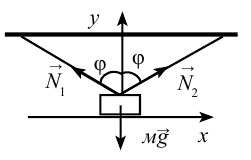
Тело массой 10 кг подвешено на двух нерастяжимых тросах. Они остаются в равновесном состоянии, образуя между собой угол равный 60 0 . Вычислите силу натяжения тросов.

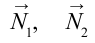
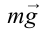
Согласно чертежу, действующие на груз силы и пересекаются в одной точке.
Следовательно, условие равновесия определяется двумя уравнениями:

После внесения математических изменений получим: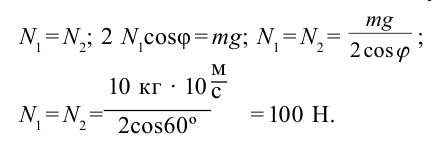

Ответ: 100 Н.

Видео:Физика 10 класс (Урок№14 - Статика. Равновесие абсолютно твердых тел.)Скачать

Определение условия равновесия тела

По I закону Ньютона, нахождение тела в состоянии равновесия означает, что оно находится в покое или движется прямолинейно и равномерно в инерциальной системе отсчета. Ознакомимся с условиями, при выполнении которых тело остается в состоянии равновесия.

Равновесие тела при поступательном движении

Поступательное движение тела можно рассматривать как движение одной его точки — движение центра массы. В этом случае для простоты можно принять, что вся масса тела сосредоточена в центре и равнодействующая сила, действующая на тело, прикладывается к этой точке. Из законов Ньютона знаем, что ускорение данной точки равно нулю тогда, когда равнодействующая сила (геометрическая сумма всех действующих сил), прикладываемая к этой точке, равна нулю. Это условие равновесия тела при поступательном движении:

Для нахождения тела в состоянии равновесия при его поступательном движении равнодействующая сила (геометрическая сумма всех действующих на тело сил), прикладываемая к телу, должна быть равна нулю:

Если геометрическая сумма сил равна нулю, то и сумма проекций этих сил на произвольную координатную ось равна нулю:

Равновесие тела с неподвижной осью вращения

На практике очень часто бывает, что при действии на тело с неподвижной осью вращения двух численно равных, но противоположно направленных параллельных сил, оно начинает вращаться вокруг этой оси. Например, блок, ворот и другие вращаются за счет таких параллельных сил. Значит, чтобы тело с неподвижной осью вращения находилось в состоянии равновесия, не достаточно, чтобы равнодействующая сила была равна нулю. Необходимо выполнение второго условия равновесия — правила моментов.

Тело с неподвижной осью вращения находится в равновесии, если алгебраическая сумма моментов действующих на него сил относительно оси вращения равна нулю:

Рекомендую подробно изучить предметы:

Физика
Атомная физика
Ядерная физика
Квантовая физика
Молекулярная физика

Ещё лекции с примерами решения и объяснением:

Равновесие тел в физике
Давление в жидкостях и газах в физике
Закон Паскаля
Закон Архимеда
Явление самоиндукции
Закон электромагнитной индукции
ЭДС индукции в движущемся проводнике
Производство, передача и потребление электрической энергии

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.