Уравнение равновесия двухфазной двухкомпонентной системы

Фазовые равновесия в двухкомпонентных системах

Двухкомпонентными называются системы, образованные двумя компонентами, которые могут быть как простыми веществами, так и химическими соединениями. Состояние двухкомпонентной системы может быть охарактеризовано четырьмя параметрами:

давлением p температурой T содержанием х одного компонента (х – мольная доля вещества в системе) содержанием (1- х) другого компонента.

Для двухкомпонентных систем обычно принимают постоянными температуру T или давление p и рассматривают соответственно изотермические p-x или изобарные T-x диаграммы состояния. В конденсированных системах роль давления обычно невелика, и в качестве параметров состояния таких систем выбирают температуру T и состав x (концентрацию одного из компонентов).

Двухкомпонентные Т-х диаграммы наиболее удобны и, следовательно, распространены. Они показывают, какие фазовые превращения происходят в двухкомпонентной системе при определенных соотношениях компонентов в зависимости от температуры. Также с помощью данных диаграмм можно понять, что будет происходить с двухкомпонентной системой при определенной температуре, если к ней добавлять один из присутствующих компонентов. В данных диаграммах по горизонтали откладывается мольная (реже массовая) доля одного из компонентов, по вертикали – температура.

Рис.1. Система координат для построения диаграмм двухкомпонентных систем

Фигуративная точка (а) на рис.1. указывает на то, что двухкомпонентная система состава XА и XB находится при температуре ТА.

Различают два вида диаграмм состояния двухкомпонентных систем: диаграммы плавкости и диаграммы растворимости.

Такие диаграммы служат для установления условий равновесия между твёрдыми и жидкими фазами (система т-ж).

Равновесия в системах твёрдое вещество-жидкость встречаются при изучении различных металлических сплавов, силикатов (стекло), водных растворов солей, систем, состоящих из органических соединений и т. д. Особое значение имеют исследования зависимости температур начала и конца кристаллизации твёрдого вещества от состава системы. Графики, выражающие эту зависимость, называются диаграммами плавкости. По таким диаграммам можно судить о наличии тех или иных фаз, их числе, температуре кристаллизации смеси определённого состава и т. д.

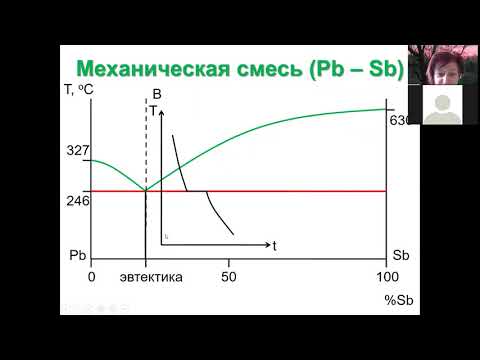
Рассмотрим наиболее простую диаграмму плавкости (рис.2.). Простейший вариант соответствует случаю, когда компоненты А и В образуют одну жидкую фазу (расплав или раствор), при охлаждении которой выделяются (кристаллизуются) только индивидуальные вещества (не образуются ни твердые растворы, ни химические соединения). Диаграммы такого типа встречаются при изучении равновесий в системах Sn-Pb, Zn-Cd, бензол-нафталин, NaCl-вода, KCl-вода и др.

Рис. 2. Диаграмма плавкости двухкомпонентной системы А-В (диаграмма состояния системы с простой эвтектикой). TA – температура кристаллизации вещества А; TB – температура кристаллизации вещества В.

На диаграмме каждое поле является областью в координатах температуры и состава, в которых существует одна или две фазы. На данном рисунке все поля подписаны. Для начала давайте попробуем эту диаграмму описать. Что мы на ней можем увидеть? Большую часть диаграммы занимает однофазная жидкость L (она представляет собой смесь жидких веществ А и В). При определенных температурах в данной жидкости начинают образовываться различные твердые фазы. Линия на фазовой диаграмме, отделяющая полностью жидкую систему от системы, в которой присутствуют твердые фазы, называется ликвидусом или линией начала кристаллизации. Она состоит из двух ветвей ТАЕ и ТВЕ.

Линия ликвидуса (или линия жидкости) – линия, изображающая зависимость от состава температуры начала выделения из жидкой фазы твёрдого компонента (начала равновесной кристаллизации). Выше линии ликвидуса находится область жидкости L.

Линия, отделяющая полностью твердофазную систему от системы, в которой присутствуют жидкие фазы, называется солидусом или линией конца первичной кристаллизации. На диаграмме это линия MN.

Линия солидуса (или линия твёрдой фазы, или эвтектическая прямая) – линия, изображающая зависимость от состава температуры окончания равновесной кристаллизации при охлаждении (или начала плавления при нагревании). Ниже линии солидуса расположено фазовое поле твёрдого состояния системы (поле SA + SB), отвечающее условиям существования механической смеси твёрдых веществ А и В

Между линиями ликвидуса и солидуса находятся поля сосуществования жидкой фазы с твёрдыми А и В (поля L + SA и L + SB).

Точка пересечения линий ликвидуса ТАЕ и ТВЕ называется точкой эвтектики Е. Эвтектическая точка показывает температуру ТЕ и состав расплава, который одновременно находится в равновесии с кристаллами вещества А и вещества В. Расплав, соответствующий точке Е, называется эвтектическим расплавом (эвтектической смесью или эвтектикой).

Эвтектика – это смесь веществ, имеющая минимальную температуру замерзания. Температура ТЕ называется эвтектической температурой; это минимальная температура замерзания смеси веществ.

Смесь кристаллов А и В, которая одновременно выпадает при температуре ТЕ, называется твёрдой эвтектикой. Твёрдая эвтектика состоит из двух твёрдых фаз (кристаллов А и В).

Таким образом, диаграмма плавкости разделена на четыре участка: L (расплав или жидкость), L + SA (расплав + кристаллы вещества А), L + SB (расплав + кристаллы вещества В), SA + SB (кристаллы вещества А + кристаллы вещества В).

Рассмотрим процесс охлаждения расплава, заданного фигуративной точкой С на диаграмме. (Фигуративной называется любая точка на диаграмме, характеризующая температуру и состав системы в целом).

Рис.3. Процесс охлаждения расплава, заданного фигуративной точкой С.

При охлаждении жидкой фазы из начального состояния С фигуративная точка системы в целом движется вниз по прямой. В точке К её пересечения с линией ликвидуса начинается кристаллизация компонента В. Система становится двухфазной. По мере кристаллизации вещества B жидкость обогащается компонентом А. Состав жидкости изменяется по ветви ликвидуса ТВЕ.

При дальнейшем охлаждении системы продолжается понижение температуры и выпадение кристаллов B из расплава. Для определения состава расплава в фигуративной точке D проведём через эту точку горизонтальную линию OQ, которая называется коннодой (нодой). По точкам O и Q определяют температуру и состав равновесных фаз. Точка Q – состав твёрдой фазы (100% кристаллы B), точка O – состав расплава (жидкой фазы).

Состав фаз, находящихся в равновесии, определяется правилом рычага:

если одна фаза при изменении параметров системы разлагается на две другие фазы, то количественное соотношение образующихся фаз будет обратно пропорционально длинам отрезков от точки состава исходной фазы до точек состава образующихся фаз.

В точке F пересечения прямой CF с линией солидуса MN начинается кристаллизация компонента А. Система становится трёхфазной (жидкость и две твёрдые фазы А и В). Происходит эвтектическая кристаллизация. Раствор имеет эвтектический состав, кроме того, соотношение масс кристаллов А и В в выпадающей эвтектике должно быть таким же, как и массовое содержание веществ А и В в расплаве эвтектического состава.

В связи с тем, что кристаллы А и В при кристаллизации твёрдой эвтектики выпадают одновременно и у них нет условий для роста, твёрдая эвтектика имеет мелкокристаллическое строение.

Застывший расплав состава F при температуре ниже TE состоит из сравнительно крупных кристаллов В, которые выпадали в интервале температур между точками K и F, и мелкокристаллической смеси кристаллов А и В в твёрдой эвтектической смеси. В точке G продолжается охлаждение двух твёрдых фаз.

Линия CKOE называется путь кристаллизации. Она показывает изменение состава жидкой фазы от начала процесса охлаждения расплава до её исчезновения.

Определим число степеней свободы различных точек на диаграмме (рис. 4.).

Для конденсированных систем правило фаз можно записать следующим образом:

Точка C — чистый компонент А, К=1, Ф=2, С=1-2+1=0, система безвариантна.

Точка D — чистый компонент В, К=1, Ф=2, С=1-2+1=0, система безвариантна.

Рис. 4. Иллюстрация к определению степеней свободы.

Точка m: К=2 (вещества А и В), Ф=1 (жидкая фаза), С=2-1+1=2, система бивариантна, т. е. можно в определённых пределах вводить любой из двух компонентов и изменять температуру – система будет оставаться гомогенной.

Точка n: К=2 (вещества А и В), Ф=2 (жидкая и твёрдая фазы), С=2-2+1=1, система одновариантна, т. е. без изменения числа фаз можно менять только один параметр – либо температуру, либо состав смеси.

Точка k: К=2 (вещества А и В), Ф=2 (твёрдое вещество А и твёрдое вещество В), С=2-2+1=1, система одновариантна.

Точка Е: К=2 (вещества А и В), Ф=3 (твёрдое вещество А, твёрдое вещество В и жидкая фаза), С=2-3+1=0, система безвариантна. Точка Е характеризуется строго определённым составом XA и XB, а также температурой TE.

Процесс охлаждения расплава, заданного точкой С

Видео:09 Фаз диагр двухкомп сист 1 принципы и мех смесьСкачать

Равновесий в двухкомпонентных системах

Проблема классификации бинарных диаграмм фазовых равновесий является одной из важных, но трудно разрешимых проблем физико-химического анализа [7].

В зависимости от характера взаимодействия компонентов различают разные типы двойных систем и их диаграмм состояния. Классификация этих типов нужна, прежде всего, для установления общих связей между различными диаграммами состояния и обоснования их эволюции при изменении физико-химических свойств компонентов и внешних условий. Кроме того, для начинающих изучать диаграммы состояния двойных систем важно их деление на разные группы и последовательность рассмотрения этих групп.

До настоящего времени не предложено какого-либо одного приз­нака, на основе которого можно было бы провести исчерпывающую классификацию двойных систем и их диаграмм состояния.

Материаловеды обычно работают с веществами, находящимися в твердом состоянии, поэтому двойные (и более сложные) системы часто разделяют на две группы в зависимости от того, какие фазы образуются в этих системах: твердые растворы на основе компонентов и промежуточные фазы.

Твердые растворы на основе компонентов могут быть непрерыв­ными или ограниченными (граничными). Промежуточные фазы на диаграммах состояния располагаются между граничными растворами на основе компонентов (или между другими промежуточными фазами, если их несколько в той или иной системе). К промежуточным фазам относятся химические соединения (фазы постоянного состава) и твердые раство­ры на их основе (фазы переменного состава), а также твердые раство­ры на основе несуществующих полиморфных модификаций компонен­тов, образующиеся в результате так называемого концентрационного полиморфного превращения.

Дальнейшее деление систем первой группы может быть проведено с учетом вариантности преобладающего фазового равновесия, в котором участвуют твердые растворы на основе компонентов, а деление систем второй группы — с учетом протяженности области гомогенности про­межуточных фаз на диаграмме состояния при заданной температуре.

Следует отметить, что моно- и нонвариантные равновесия встреча­ются не только в системах с твердыми растворами на основе компо­нентов, но и в системах с промежуточными фазами, в которых также могут образовываться непрерывные, а чаще — граничные растворы на основе компонентов.

Деление промежуточных фаз на фазы постоянного и переменного состава в значительной степени условно, так как в природе вообще и в металлических системах в частности не встречаются фазы постоян­ного состава (т.е. определенные химические соединения), а всегда имеются фазы переменного состава, однако часто области гомоген­ности этих фаз настолько узки (как и области граничных растворов на основе компонентов), что ими можно пренебречь.

Из правила фаз (1.7) следует, что моновариантное равновесие в двойных системах — это равновесие двух фаз (С = 1 при Ф = 2 и К = 2). В зави­симости от агрегатного состояния и кристаллической структуры фаз можно представить следующие двухфазные равновесия: L ⇄ α − рав­новесие жидкого и твердого раствора на основе одного из компонен­тов; α₁ ⇄ α₂ − равновесие двух твердых растворов на основе одного или разных компонентов (оба раствора имеют одинаковую кристалли­ческую структуру и отличаются только химическим составом); α ⇄ β −равновесие двух твердых растворов на основе одного или разных компонентов (оба раствора имеют разную кристаллическую структуру и отличаются химическим составом) и α ⇄ α’ − равновесие неупо­рядоченного и упорядоченного твердых растворов (оба раствора имеют разную кристаллическую структуру и могут отличаться химическим составом).

Отсюда следует, что среди систем с моновариантными равнове­сиями можно выделить, по меньшей мере, четыре подгруппы систем с одним из перечисленных выше равновесий. К этим равновесиям можно добавить равновесие двух жидких растворов L₁ ⇄ L₂ на основе одного или разных компонентов, наблюдаемое при ограниченной растворимости компонентов в жидком состоянии (расслоении). Как единственное (преобладающее) равновесие L₁ ⇄ L₂ в металлических системах не встречается, а всегда предшествует одному из нонвариантных (трехфазных) равновесий.

Согласно правилу фаз (1.7), максимально возможное число равновесных фаз в двойной системе равно трем (С = 0 при К = 2 и Ф = 3). Следова­тельно, нонвариантное равновесие в двойных системах — это трехфаз­ное равновесие. Любое нонвариантное равновесие, в том числе и трех­фазное, характеризуется максимальной устойчивостью – неизменностью внутренних параметров, проявляющейся тем, что, во-первых, реализуется при постоян­ной температуре и, во-вторых, при неизменных составах всех равно­весных фаз.

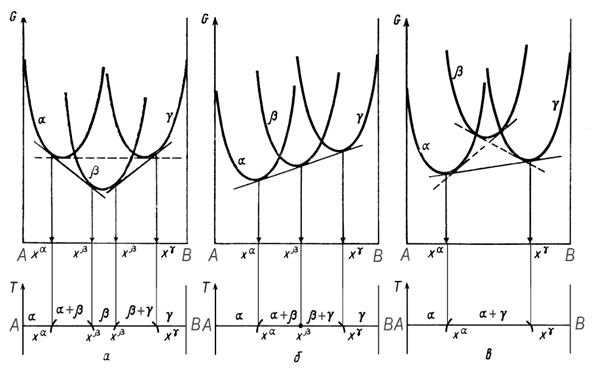
Характер процессов, происходящих вблизи температуры трехфазного равновесия, удобно проиллюстрировать графически с помощью диаграмм Гиббса – Розебома (рисунок 4.1).

Рисунок 4.1. Изменение взаимного положения кривых G_x вблизи температуры (а и в) и при температуре (б) трехфазного равновесия в бинарной системе А — В

При понижении температуры фазовое равновесие зависит от того, будет ли кривая энергии Гиббса промежуточной по составу β-фазы, отставать от кривых G α и G γ (точнее, от общей касательной к ним) или опережать их [11].

Рисунок 4.2. Два вида трехфазных равновесий в бинарной системе

а- эвтектическое; б – перитектическое.

В первом случае при температуре, превышающей температуру трехфазного равновесия, устойчивость α + β- и β + γ — равновесий окажется выше, чем у 𝛼 + γ(рис. 4.1, а). При снижении температуры возникнет собственно трехфазное равновесие (рис. 4.1, б), которое при дальнейшем понижении температуры сменится равновеси­ем 𝛼 ⇆ γ, а β-фаза становится неустойчивой. Вид полученной диаграммы приведен на рис. 4.2, а.

Для состава, соответ­ствующего х β — в трехфазном равновесии, понижение температуры сопровождается реакцией β ⇄ α + γ, протекающей при температуре трехфазного равно­весия. По наиболее изученному представителю (β-фаза — жидкость, α- и γ-фазы — твердые) оно получило название равновесия эвтектичес­кого типа, поскольку равновесие L ⇄ α + γ называется эвтектикой. С повышением температуры будут наблюдаться обратные процессы.

Процесс (рисунок 4.2, б), идущий при температуре трехфазного равнове­сия в сплаве состава х β при охлаждении, может быть описан так: α + γ ⇄ β. Такое равновесие называют равновесием перитектического типа — по названию превращения L + γ ⇄ β. Других типов трехфазных равновесий в двойной системе быть не может. Соответствующие этим равновесиям графические образы выделены овальной областью на рис. 4.2.

Основные типы нонвариантных фазовых равновесий в бинарных системах

и их графические образы

№ п.п.	Аналитический вид равновесия	Графический образ равновесия	Название равновесия
Равновесия эвтектического типа
1.1	L ⇄ α + β		эвтектическое
1.2	L1⇄ L2 + β		монотектическое
1.3	β ⇄ α + γ		эвтектоидное
Равновесия перитектического типа
2.1	L + γ ⇄ β		перитектическое
2.2	L1 + L2 ⇄ β		синтектическое
2.3	β + γ ⇄ α		перитектоидное

Анализ сказанного позволяет выделить шесть основных видов нонвариантных равновесий, разделив, в свою очередь, на две большие групп: равновесия эвтектического и перитектического типов. К равновесиям эвтектического типа относятся три основных вида: эвтектическое, монотектическое и эвтектоидное. Равновесия перитектического типа объединяют перитектическое, синтектическое и перитектоидное равновесия. Схема этой классификации с представлением графических образов нонвариантных равновесий представлена в таблице1.1.

В двойных системах встречаются сле­дующие нонвариантные равновесия с участием одной или двух жидких фаз: синтектическое L₁ + L₂ ⇄ α; монотектическое L₁⇄ L₂ + β; эв­тектическое L ⇄ α + β; перитектическое L + β ⇄ α и метатектическое β ⇄ L + α, где α и β — граничные растворы на основе компонентов (или промежуточные фазы).

Синтектическое и метатектическое равновесия в металлических системах встречаются сравнительно редко.

В твердом состоянии возможны следующие нонвариантные равно­весия: эвтектоидное α ⇄ β +𝛾; монотектоидное β₁ ⇄ α + β₂ и перитек-тоидное β + γ ⇄ 𝛼.

Монотектоидное равновесие напоминает эвтектоидное, но отличает­ся от него тем, что β₁— и β₂ — растворы имеют одинаковую кристалличес­кую структуру, но разный химический состав. При температурах выше критической составы этих растворов становятся идентич­ными.

Видео:Уравнения состояния. Фазовое равновесиеСкачать

Правило фаз Гиббса

Содержание:

Правило фаз (или правило фаз Гиббса) — соотношение, связывающее число компонентов, фаз и термодинамических степеней свободы в равновесной термодинамической системе. Роль правила фаз особенно велика при рассмотрении гетерогенных равновесий в многофазных многокомпонентных системах.

На странице -> решение задач по химии собраны решения задач и заданий с решёнными примерами по всем темам химии.

Видео:Фазовые равновесия | ФизхимияСкачать

Правило фаз Гиббса

Правило фаз Гиббса утверждает, что число степеней свободы С равновесной термодинамической системы равно разности между числом компонентов К и числом фаз Ф, плюс число факторов п, влияющих на равновесие.

Независимые компоненты и степени свободы системы

Представления о гомогенных и гетерогенных системах и фазах, изложенных в предыдущей главе, следует дополнить понятиями о компонентах и степенях свободы. Компонентами называют индивидуальные вещества системы, концентрации которых определяют состав всех ее фаз, т. е. веществ в системе может быть больше, чем требуется для описания состава всех ее фаз. Например, при установлении равновесия

система состоит из трех веществ, но для описания состава всех трех фаз достаточно знать любые два, их называют независимыми компонентами; состав третьей фазы легко определить, используя уравнение вещественного баланса. Из приведенного примера следует: число независимых компонентов равновесной системы равно общему числу индивидуальных веществ минус число связывающих их уравнений. При наличии химических реакций число независимых компонентов системы меньше числа индивидуальных веществ. Если же между веществами нет химического взаимодействия, то числа независимых компонентов и индивидуальных веществ совпадают (например, воздух состоит из такого же числа независимых компонентов, сколько сортов молекул входит в его состав).

Степенями свободы (С) равновесной системы называют те параметры, которые можно произвольно изменять, не меняя числа и природы фаз системы. Степенями свободы могут являться концентрации реагирующих веществ в фазах переменного состава (растворах), давление, температура.

Число степеней свободы определяют разностью между общим числом независимых переменных системы и числом уравнений, их связывающих. В приведенном выше примере общее число переменных равно двум (температура и давление С02 или его концентрация), уравнение одно, следовательно, число степеней свободы С данной системы равно: 2—1 = 1.

Количественное соотношение между числами степени свободы (С), фаз (Ф) и независимых компонентов (К), получившее название правила фаз, выведено В. Гиббсом (1876), оно имеет вид

Здесь 2 — число переменных параметров системы (давление и температура). Использование этого правила помогает при изучении химических реакций и равновесных систем.

Рассмотрим некоторые конкретные примеры.

Пример 1. Система представлена равновесием

Число независимых компонентов К равно разности числа индивидуальных веществ и числа уравнений, их связывающих, следовательно,В системе три фазы (две твердые и одна газообразная). Используя правило фаз (7.1), вычисляем число степеней свободы: Следовательно, в этой системе без изменения числа и природы фаз произвольно можно изменять только один параметр. Если произвольно задать температуру, то этим уже будет использована единственная степень свободы и все другие параметры примут строго определенное, независимое от нашего желания значение.

Связь с температурой и природой реагирующих веществ выражается уравнением Единственными переменными величинами в этом уравнении будут рсо и Т. Задав произвольно одну из них в качестве аргумента, получим строго определенное значение другой. Это и означает, что данная система имеет только одну степень свободы.

Пример 2. Пусть система представлена равновесием

Число независимых компонентов в ней равнот. е. система двухкомпонентна. Все вещества системы газообразны, следовательно, фаза одна. Используя правило фаз (7.1), вычисляем число степеней свободы СЭто означает, что три любых параметра этой системы могут быть заданы произвольно (всего таких параметров четыре: температура и три концентрации или парциальных давления) в следующих комбинациях:

Это легко понять, если записать выражение температурной зависимости константы равновесия:

Следовательно, чтобы определить значение любой из переменных, нужно задать значения остальных трех.

Пример 3. Пусть система представлена ненасыщенным водным раствором хлористого натрия NaCl. В растворе, помимо молекул воды имеются ионы Единственное связывающее их уравнение —

Эта однофазная система представлена тремя индивидуальными фермами соединений и одним уравнением, отсюда число независимых компонентов в этой однофазной системе равно

Поскольку газовая фаза (пар над раствором) не входит в рассматриваемую систему (по условию), то в выражении правила фаз Гиббса число параметров должно стать на единицу меньше, т. е. К + 1, тогда С = 2 +1 — 1 = 2. Следовательно, данная система имеет две степени свободы—температуру и концентрацию раствора.

Однокомпонентные системы

Наиболее просты системы, состоящие из одного компонента. Каждая однокомпонентная система представлена единственным веществом, находящимся в различных агрегатных состояниях. Так, например, вода может существовать в парообразном, жидком и кристаллическом состояниях, каждое из которых устойчиво в определенных интервалах температуры и давления.

Переменными параметрами . однокомпонентных систем могут служить только давление и температура, поскольку состав фаз по условию постоянен. Поэтому состояние однокомпонентных систем может быть представлено в виде зависимости давления от температуры:

Графическое изображение такой зависимости получило название диаграммы состояния или фазовой диаграммы

состояния, поскольку состав фаз в однокомпонентной системе одинаков и при изменении условий не меняется.

Давление пара в процессах па рообра зова ни я уста на вл ивается и над твердыми, и над жидкими веществами:

Характер этой функциональной зависимости приведен на графике рис. 7.1. Точка плавления кристаллической фазы находится .совместным решением приведенных выше уравнений; исходя из условия равенства жидкой и кристаллической фаз должно выполняться условие В результате для точки плавления имеем

При переходе из кристаллического состояния в пар (сублимация) степень разупорядоченности движения частиц больше, чем при испарении (в жидкости беспорядочность движения частиц больше, чем в кристаллах), поэтому величина положительна:

Поскольку температура может принимать только значения Т > 0, величина всегда положительна:

Точно так же обстоит дело с полиморфными превращениями, если они есть.

Зависимость температуры плавления чистых веществ от давления p = fT можно определить уравнением Клаузиуса— Клайперона (приближенная форма):

В этом уравнении являются объемами 1 моль соединения в расплавленном и кристаллическом состояниях соответственно. Если то правая часть уравнения положительна, если —то отрицательна.

На рис. 7.2, а, б показано, что каждому из условий соответствует определенный наклон линии р = f(Т). Крутой ход кривых в равновесии между двумя конденсированными фазами объясняют незначительной разностью

Рассмотрим в качестве примера однокомпонентную систему вода—лед—пар. С точки зрения правила фаз Гиббса для такой системы Следовательно, эта система максимально может быть трехфазной (ф=3) при числе степеней свободы, равном нулю (С = 0). Этому случаю соответствует равновесие вода—лед—пар при строго определенных температуре (273 К) и давлении

Равновесие двух фаз (испарение, сублимация) характеризуется одной степенью свободы (произвольны давление или температура). Двухфазные превращения описываются следующими уравнениями:

(получено экспериментально).

При использовании этих данных на рис. 7.3 построен график зависимости р =f(Т), получивший название диаграммы’; состояния воды. Линии (а), (b) и (с) отвечают равновесиям двух фаз: твердое вещество— пар; твердое вещество— жидкость; жидкость— пар соответственно. Точка пересечения трех кривых носит название тройной точки, она отвечает равновесию всех трех фаз, а участки диаграммы I, II и III отвечают однофазному равновесию с тремя степенями свободы. Линия (b) имеет отрицательный наклон, соответствующий отрицательному значению Следовательно, при замерзании воды ее объем увеличивается. Этот известный факт объясняется тем, что кристаллическая структура льда содержит большое число пустот. При плавлении льда такая структура в значительной степени разрушается, пустоты заполняются молекулами воды и ее объем уменьшается. Веществ с такой аномалией известно немного; кроме воды можно назвать элементарные висмут и галлий; из соединений — оксид бора. Все остальные вещества имеют положительный наклон линии b на диаграмме состояния.

Двухкомпонентные системы

Перейдем к характеристике более сложных, двухкомпонентных систем. С точки зрения правила фаз число степеней свободы в системах с К = 2 может максимально быть равным 3, если Ф= 1. Это означает, что кроме таких переменных параметров системы, как давление и температура, появляется третий— концентрация раствора. Примером однофазных систем переменного состава, образованных двумя и более независимыми компонентами, служат растворы. Растворы образуются во всех агрегатных состояниях. Они могут быть газообразными, жидкими и твердыми.

Все газы в любых соотношениях между собой неограниченно растворимы. Только при низких температурах и очень высоких давлениях в некоторых газовых смесях наблюдается расслоение. В жидком состоянии ограничение растворимости наблюдают довольно часто. Однако с повышением температуры растворимость обычно возрастает, так что многие жидкие смеси, расслоенные на две фазы, с повышением температуры становятся однофазными. Наиболее важные группы жидких растворов следующие:

1) водные, неводные и органические растворы;

2) солевые расплавы галогенидных, кислородных и сульфидных соединений (при высоких температурах);

3) расплавы металлов (при высоких температурах).

В твердом состоянии ограничение в растворимости также имеет место. Известны три типа твердых растворов: замещения, внедрения и вычитания. Твердые растворы замещения обычно образуются двумя или несколькими различными элементами, так что в кристаллической структуре места атомов одного элемента неупорядоченно замещаются атомами второго элемента. В результате распределение каждого из элементов оказывается хаотическим, а соотношение между количествами атомов того и другого сорта — произвольным. Примерами твердых растворов замещения служат сплавы меди и никеля или смешанные кристаллы хлористого и бромистого натрия. Твердые растворы внедрения получают чаще всего при растворении небольших по размеру атомов неметаллов в металлической решетке, например раствор углерода в железе. В этом случае атомы неметаллов (Н, В, С, О и др.) хаотически и в произвольных соотношениях располагаются в промежутках между атомами металла.

Твердые растворы вычитания, или дефектные структуры, характеризуются наличием пустот, которые размещаются хаотически и создают беспорядок в расположении мест, занятых атомами элементов. Примером таких структур служит сульфидный минерал пирротин, монотонно изменяющий свой состав в пределах

Общая характеристика растворов

Процесс растворения— сложный физико-химический акт, а не простое распределение частиц одного вещества между частицами другого, которое в какой-то степени применимо для описания разреженных газовых смесей. В жидких и твердых растворах частицы растворителя и растворенного вещества непосредственно взаимодействуют между собой и находятся на таких коротких расстояниях, как и в химических соединениях. Взаимодействие молекул растворителя с растворяемым веществом зависит от сил разнообразной природы, за счет которых в растворе образуются устойчивые комплексные и полимерные соединения, способные существовать вне раствора,— сольваты, а в случае водных растворов—гидраты.

Одна из важнейших количественных характеристик растворов, связанная через закон действующих масс с энергетикой процессов растворения,— концентрация раствора. Поэтому целесообразно вспомнить некоторые наиболее используемые способы выражения концентраций, кроме уже упомянутых молярности и молярной доли следует знать массовую и объемную доли, моляльную концентрацию (моляль-ность), титр.

Поскольку процессы растворения имеют сложную химическую природу, законы, определяющие растворение и отражающие природу растворов, сложны. Для упрощения введено понятие идеального раствора, простейшими примерами которого могут служить разреженные газы. В реальных газах соотношение между объемом, давлением и температурой описывается уравнением Ван-дер-Ваальса

В этом уравнении слагаемые учитывают силовое взаимодействие между частицами газа. В разреженных газах при достаточно высокой температуре эти слагаемые столь незначительны по величине, что ими можно пренебречь с большой степенью точности. В результате получаем уравнение Клапейрона относящееся к разреженным газам, у которых тепловой эффект взаимодействия между частицами равен нулю.

Составляя смеси таких газов, можно убедиться в том, что для их взаимодействия справедливо условие и полная аддитивность парциальных объемов и давлений, т. е.

Газовые растворы, которые образуются из составляющих их частей с нулевым тепловым эффектом, а объем их смеси в точности равен сумме объемов частей, получили название идеальных.

Для жидких и твердых растворов также существует понятие идеальности, в общем виде оно может быть сформулировано следующим образом: идеальными называют растворы, которые образуются из составных частей при выполнении условий

Примерами идеальных растворов могут служить газовые смеси изотопов, а также все разбавленные растворы. И действительно, добавление к растворителю небольшого количества растворяемого вещества мало изменяет свойства растворителя и раствора, и условие идеальности (7.2) справедливо. Но свойства растворяемого вещества в таком растворе далеки от идеальных.

Концентрированные растворы но свойствам не близки к идеальным, однако для получения грубой качественной картины их можно описывать с помощью модели идеальных растворов. Для строгого решения производственных и научных задач требуется обязательное введение поправок на реальность.

Услуги по химии:

Лекции по химии:

Лекции по неорганической химии:

Лекции по органической химии:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

📽️ Видео

09 Фазовые диаграммы 2 правило фазСкачать

Лекция «Диаграмма состояния двухкомпонентных сплавов»Скачать

Фазовые диаграммыСкачать

Коробов М. В. - Физическая химия. Часть 1 - Двухкомпонентные системы. Правило КоноваловаСкачать

Фазовые диаграммы. Тройная точка. Критическое состояние вещества. 10 класс.Скачать

09 Фаз диагр двухкомп сист 4 огранич растворыСкачать

Урок 70. Виды равновесия. Условие равновесия тела при отсутствии вращения.Скачать

09 Фаз диагр двухкомп сист 3 растворыСкачать

Румянцева М.Н.- Общая и неорганическая химия. Лекции - 4.Фазовые равновесияСкачать

09 Фаз диагр двухкомп сист 2 соединениеСкачать

Фазовое равновесие в однокомпонентных системах. СеминарСкачать

Физика 10 класс (Урок№14 - Статика. Равновесие абсолютно твердых тел.)Скачать

Коробов М. В. - Физическая химия. Часть 1 - Фазовые диаграммы. Фазовые переходыСкачать

Двухфазное КЗ на векторных диаграммахСкачать

Физическая химия. Лекция 2. Термодинамика фазовых равновесийСкачать

Савченко А. М. - Термодинамика и статистическая физика I - Фазовые переходыСкачать

Техническая механика/ Определение равнодействующей. Плоская система сходящихся сил.Скачать