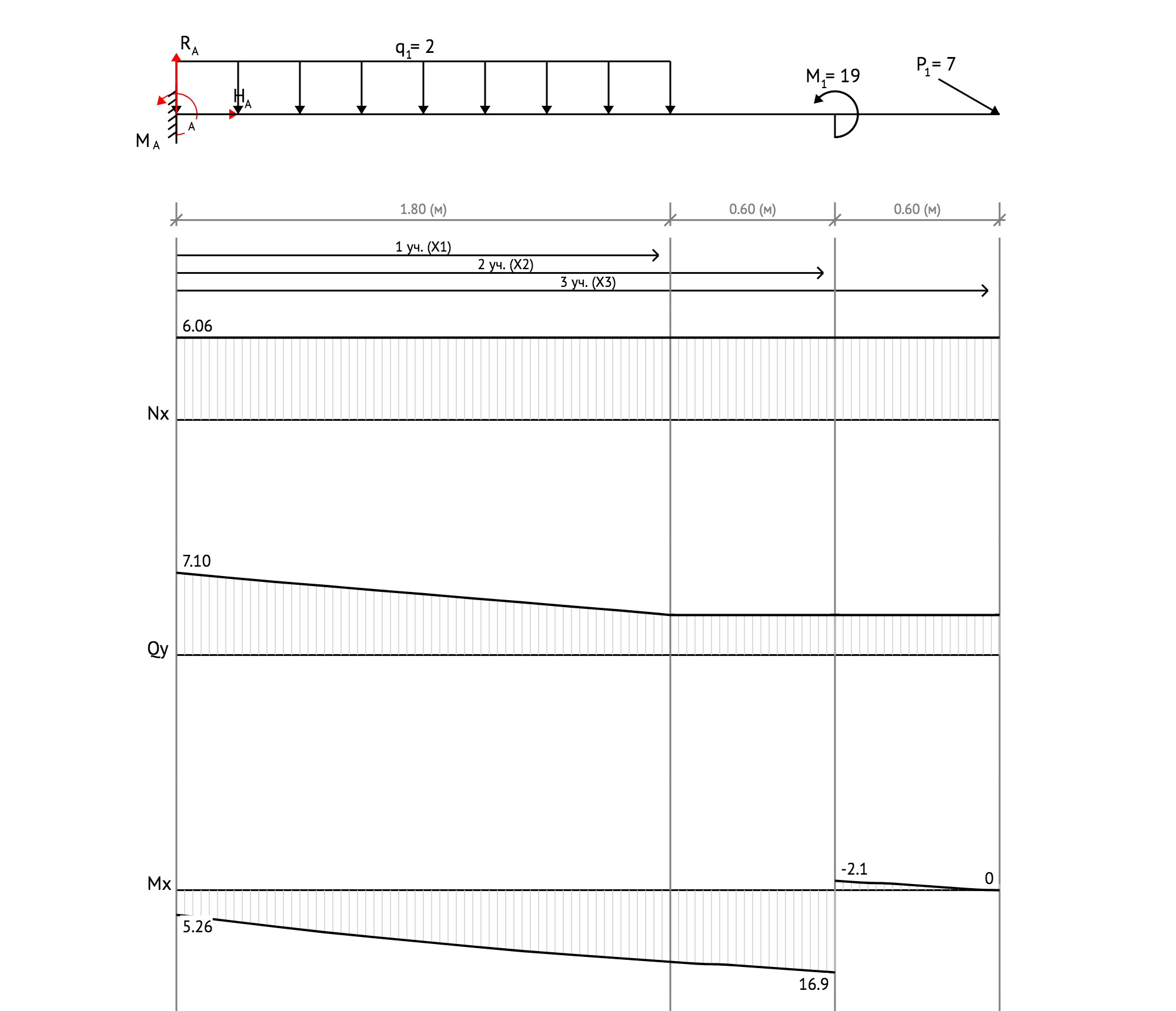
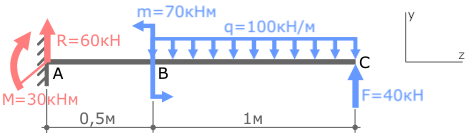
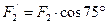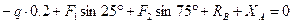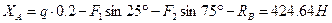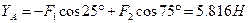Уравнение равновесия балки с жесткой заделкой (3 видео)

Содержание

Пример №3. Консольная балка (жесткая заделка слева)
Определение опорных реакций
Построение эпюр
Определение реакций жесткой заделки балки.
iSopromat.ru
Задача
Пример решения
Решение задач, контрольных и РГР
🔍 Видео

Видео:Определение опорных реакций балки. Сопромат для чайников ;)Скачать

Пример №3. Консольная балка (жесткая заделка слева)

Определение опорных реакций

Согласно схеме решения задач статики определяем, что для нахождения неизвестных реакций необходимо рассмотреть равновесие балки.
1. На балку наложена связь в точке A (слева) типа жесткая заделка, поэтому освобождаем балку, заменив действие связи реакциями (H_A, R_A, M_A).
2. Определим реакции опор в соответствии с уравнениями равновесия балки: ΣF_x=0, ΣF_y=0, ΣM_A=0.
ΣF_x=0: H_A + P₁*cos(30)=0
ΣF_y=0: R_A — q₁*1.8 — P₁*sin(30)=0;
ΣM_A=0: M_A — q₁*1.8*(1.8/2) + M₁ — 3*P₁*sin(30)=0;
3. Решаем полученную систему уравнений, находим неизвестные:
H_A=- P₁*cos(30)=- 7*0.8660=-6.06 (кН), так как реакция отрицательна, на расчетной схеме направим ее в противоположную сторону.
R_A=q₁*1.8 + P₁*sin(30)=2*1.8 + 7*sin(30)=7.10 (кН)
M_A=q₁*1.8*(1.8/2) — M₁ + 3*P₁*sin(30)=2*1.8*(1.8/2) — 19 + 3*7*sin(30)=-5.26 (кН*м), так как момент отрицателен, на расчетной схеме направим его в противоположную сторону.
4. Выполним проверку, составив дополнительное моментное уравнение отоносительно свободного конца балки:
— 3*R_A — M_A + q₁*1.8*(1.2+1.8/2) + M₁ + 0*P₁*sin(30)=- 3*7.10 — 5.26 + 2*1.8*(1.2+1.8/2) + 19.00 + 0*7*sin(30)=0

Построение эпюр

Рассмотрим второй участок 1.8 ≤ x₂

Видео:Определение опорных реакций в балке (балка с жесткой заделкой)Скачать

Определение реакций жесткой заделки балки.

МЕТОДИЧЕСКое пособие

Для выполнения практических работ по технической механике

ОП . 03 Техническая механика

«Монтаж и техническая эксплуатация промышленных и гражданских зданий»

Рекомендованы цикловой методической комиссией, Утверждены протокол №___от «___»_____________2014 г Зам.директора по УМР Председатель__________/_________________/ ________ Т.Г.Мялицина

Краевое государственное автономное образовательное учреждение среднего профессионального образования «Нытвенский промышленно-экономический техникум»

Разработчик: Губина Татьяна Николаевна, преподаватель высшей категории

Практическая работа № 1.

Определение усилий в стержнях стержневой конструкции.

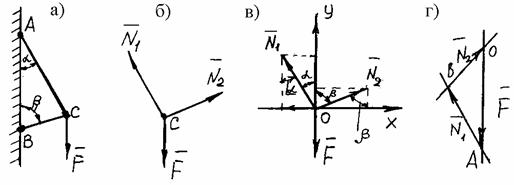
Пример 1. Стержни АС и ВС (рис. 1,а) соединены между собой шарниром С, а с вертикальной стеной — посредством шарниров А и В. В шарнире С приложена сила F = 1260 Н. Требуется определить реакцииN₁ и N₂ стержней действующие на шарнир С, если = 30° и = 60°.

Рис. 1

Решение. Рассматриваем равновесие точки С, которая считается несвободной, так как на нее наложены связи в виде стержней АС и ВС. Освобождаем точку С от связей и заменяем их силами реакций связей, считая, что стержень АС растягивается, а стержень ВС сжимается под действием силы F. Обозначим реакцию стержня АС через N₁, а реакцию стержня ВС через N₂. В итоге точка С становится свободной, находясь под действием плоской системы трех сходящихся сил: активной силы F и сил реакций N₁ и N₂ (рис. 1, б). Приняв точку О за начало координат, перенесем силы F, N₁ и N₂ параллельно самим себе в эту точку (рис. 1, в) и составляем уравнения проекций сил на оси координат:

(1)

. (2)

Умножим уравнение (1) на , получим

(3)

. (4)

После сложения уравнений (3) и (4) получим

откуда 2N₂ = F или Н. Из уравнения (1) получаем, что

или Н.

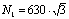
Графический метод. Для решения задачи этим методом выбираем масштаб силы F (например, 10 Н = 1 мм) и строим замкнутый треугольник сил (рис. 1, г). Из произвольной точки О проводим прямую, параллельную вектору F, и откладываем на этой прямой в выбранном масштабе вектор . Из конца вектора (точка А) проводим прямую, параллельную вектору , а из точки О — прямую, параллельную вектору . Пересечение этих прямых дает точку В. Получили замкнутый треугольник сил ОАВ, стороны которого в выбранном масштабе изображают силы, сходящиеся в точке С. Величины сил N₁и N₂ определим после измерения сторон АВ и ВО треугольника ОАВ.

Ответ: N₁ = 1089,9 H; N₂ = 630 H

Практическая работа № 2.

Определение реакций опор балки на двух опорах.

Дано: F1=15Н; F2=75Н; α=25°; β=40°; М=60Нм; q=7H/м; а=0,2м.

Определить реакции опор

1.Рассмотрим равновесие пластины. Проведем координатные оси xy, и изобразим действующие на пластину силы.

2.Для плоской системы сил составим три уравнения равновесия. Воспользуемся теоремой Вариньона: ;

Проверка:

Ответ: , ,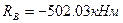

Реакция направлена противоположно показанной на рисунке.

Практическая работа № 3.

Определение реакций жесткой заделки балки.

Балки предназначены для восприятия поперечных нагрузок. По способу приложения нагрузки делятся на сосредоточенные (действуют на точку) и распределенные (действуют на значительную площадь или длину).

q — интенсивность нагрузки, кн/м

G = q L – равнодействующая распределенной нагрузки

Балки имеют опорные устройства для сопряжения их с другими элементами и передачи на них усилий. Применяются следующие виды опор:

Эта опора допускает поворот вокруг оси и линейное перемещение параллельно опорной плоскости. Реакция направлена перпендикулярно опорной поверхности.

Эта опора допускает поворот вокруг оси, но не допускает никаких линейных перемещений. Направление и значение опорной реакции неизвестно, поэтому заменяется двумя составляющими R_Aу и R_Aх вдоль осей координат.

· Жесткая заделка (защемление)

Опора не допускает перемещений и поворотов. Неизвестны не только направление и значение опорной реакции, но и точка её приложения. Поэтому заделку заменяют двумя составляющими R_Aу , R_Aх и моментом М_А. Для определения этих неизвестных удобно использовать систему уравнений.

Для контроля правильности решения используется дополнительное уравнение моментов относительно любой точки на консольной балке, например точка В ∑ m_В(F_к)= 0

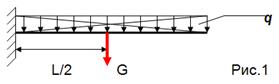
Пример. Определить опорные реакции жесткой заделки консольной балки длиной 8 метров, на конце которой подвешен груз Р = 1 кн. Сила тяжести балки G = 0,4 кн приложена посередине балки.

Освобождаем балку от связей, т.е отбрасываем заделку и заменяем её действие реакциями . Выбираем координатные оси и составляем уравнения равновесия.

Решая уравнения, получим R_Aу = G + P = 0,4 + 1 = 1,4 кн

M_A = G L / 2 + P L = 0,4 . 4 + 1 . 8 = 9,6 кн . м

Проверяем полученные значения реакций:

— 9,6 + 1,4 . 8 – 0,4 . 4 = 0

— 11,2 + 11,2 = 0 реакции найдены верно.

Для балок расположенных на двух шарнирных опорах удобнее определять опорные реакции по 2 системе уравнений, поскольку момент силы на опоре равен нулю и в уравнении остается одна неизвестная сила.

Для контроля правильности решения используется дополнительное уравнение ∑ F_kу= 0

1) Освобождаем балку от опор, а их действие заменяем опорными реакциями;

2) Заменяем распределенную нагрузку на равнодействующую G = q . L;

3) Выбираем координатные оси;

4) Составляем уравнения равновесия.

R_Ву = [G . L/2 + m]/(L + B) = [5 . 6/2 + 10](6+6) = 2,08 кн

R_Aу = [Q . (L/2 + B) — m] / (L + B) =[5 . (6/2 + 6) — 10] / (6 + 6) = 2,92 кн

Видео:Определение реакций опор в жесткой заделке консольной балкиСкачать

iSopromat.ru

Пример решения задачи по расчету реакций опоры в жесткой (глухой) заделке стальной балки, нагруженной поперечной силой F, сосредоточенным моментом m и равномерно распределенной нагрузкой q.

Видео:Определение опорных реакций в заделке ( балка ). СопроматСкачать

Задача

Рассчитать величину и направление опорных реакций в жесткой заделке консольной балки нагруженной заданной системой внешних нагрузок.

Видео:Определение реакций опор простой рамыСкачать

Пример решения

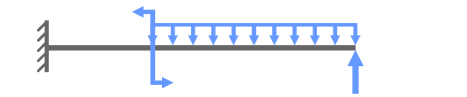
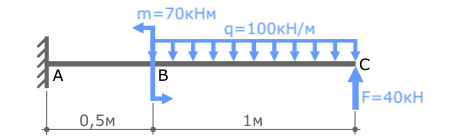
Покажем значения нагрузок и продольные размеры балки, обозначим ее характерные сечения буквами A, B и C.

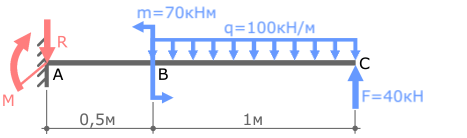
В случае плоского поперечного изгиба в жесткой заделке консольной балки могут иметь место только две опорные реакции:

Поперечная сила R
Изгибающий момент M

На данном этапе решения задачи эти реакции можно направить в любую сторону.

Короткое видео о реакциях в заделках:

Определим величину, а заодно и истинное направление опорных реакций.

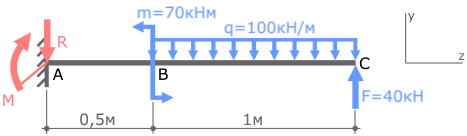
Зададим систему координат y-z.

Для нахождения двух реакций нам понадобятся два уравнения равновесия.

Балка не перемещается вверх-вниз, поэтому сумма проекций всех сил на ось y должна равняться нулю.

Проецируя все силы на ось y получаем первое уравнение:

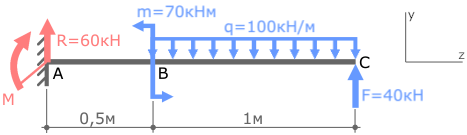
Откуда находим величину реакции R

Знак «-» в ответе говорит о том, что реальное направление реакции R противоположно выбранному вначале.

Поэтому изменим направление силы и соответственно ее знак на противоположные.

Второе уравнение статики получим из условия, что балка не вращается, так как сумма моментов приложенных к ней тоже равнв нулю.

Отсюда находим опорный момент M

Положительный результат показывает, что выбранное наугад направление момента М оказалось верным, то есть перенаправлять его не нужно.

Полученные значения опорных реакций можно легко проверить.

Для этого запишем уравнение суммы моментов относительно точки B или C:

и подставив в него полученные значения, мы должны получить сумму равную нулю

Так и есть! Значит опорные реакции определены верно.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах