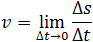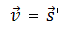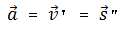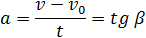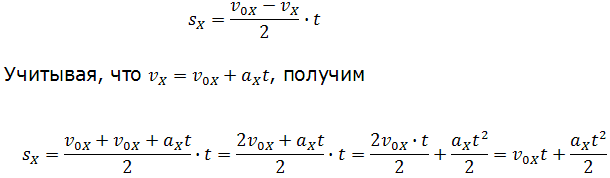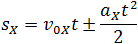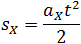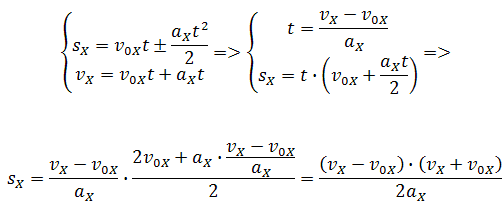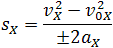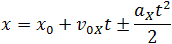Уравнение равнопеременного движения без времени (4 видео)

Равнопеременное прямолинейное движение

Равномерное прямолинейное движение – это частный случай неравномерного движения.

Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.

Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.

Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).

Равнопеременное движение может быть равноускоренным или равнозамедленным.

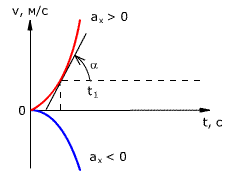
Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.

Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.

В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.

Средняя скорость переменного движения определяется путём деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости – м/с.

Мгновенная скорость – это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:

Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:

Проекция вектора скорости на ось ОХ:

это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси).

Ускорение – это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:

Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени:

Если тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой:

Знак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению. Аналогично записываются уравнения проекций вектора скорости на другие оси координат.

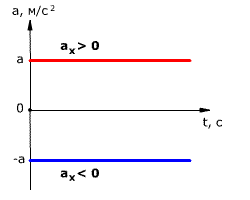
Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени, рис. 1.15).

Рис. 1.15. Зависимость ускорения тела от времени.

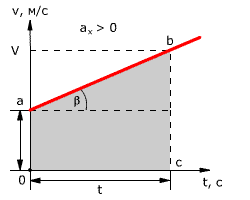
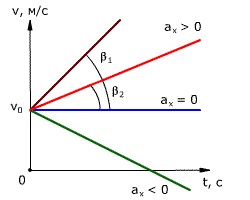
Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия (рис. 1.16).

Рис. 1.16. Зависимость скорости тела от времени.

График зависимости скорости от времени (рис. 1.16) показывает, что

При этом перемещение численно равно площади фигуры 0abc (рис. 1.16).

Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны:

Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна:

В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус).

Общая формула для определения проекции перемещения:

График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.

Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.

Рис. 1.18. Зависимость перемещения тела от времени.

Скорость тела в данный момент времени t₁ равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле:

Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:

Формула сокращённого умножения разности квадратов поможет нам вывести формулу для проекции перемещения:

Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то уравнение движения тела будет выглядеть следующим образом:

Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат. При а_x

Содержание

Как посчитать путь ускоряющегося тела не используя время
Выводим формулу пути без времени
Выражаем время из формулы для скорости
В формулу пути подставим выражение для времени
Упрощаем выражение, расположенное до знака «плюс» в правой части
Возводим в квадрат дробь
Упрощаем правую часть, записанную после знака «плюс»
Приводим к общему знаменателю дроби в правой части уравнения
Дроби с одинаковыми знаменателями складываем
Как выглядит формула пути без времени, когда скорость тела уменьшается
Выводы
Прямолинейное равнопеременное движение
🎥 Видео

Видео:УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Как посчитать путь ускоряющегося тела не используя время

Существует формула, с помощью которой можно посчитать путь, пройденный телом, когда нам известны его начальная скорость, ускорение и конечная скорость.

Сокращенно эту формулу называют «путь без времени». Так ее называют потому, что в правой ее части время t движения отсутствует (рис. 1).

Формула пути без времени помогает упростить решение некоторых задач кинематики. Особенно, задач, части C.

Однако, не торопитесь на ЕГЭ записывать эту формулу в готовом виде. Сначала в решении задачи нужно записать вывод этой формулы. И только потом ее можно использовать.

Формулу выводят из выражений для равнопеременного движения. Сейчас я помогу вам вывести эту формулу с помощью нескольких простых шагов.

Видео:Физика - уравнения равноускоренного движенияСкачать

Выводим формулу пути без времени

Для определенности будем считать, что тело движется по прямой все быстрее и быстрее. То есть, скорость тела увеличивается, так как появляется ускорение.

В таком случае векторы ускорения и скорости тела будут сонаправленными (параллельными и направленными в одну и ту же сторону).

Сонаправленные или противоположно направленные векторы называют коллинеарными векторами. Прочитайте подробнее о коллинеарных векторах.

Чтобы вычислить путь тела, когда скорость его увеличивается, нужно использовать две формулы:

( large v_ left( frac<text> right)) – начальная скорость тела;

( large v left( frac<text> right)) – конечная скорость;

( large a left( frac<text><c^> right)) – ускорение тела;

( large S left( text right)) – путь, пройденный телом;

(large t left( c right)) – время, за которое тело прошло этот путь.

В формуле для пути S присутствует время t. Получим из нее формулу для пути, в которой время будет отсутствовать.

Что сделать, чтобы получить формулу пути, в которой отсутствует время:

сначала получить выражение для времени t из уравнения для скорости;
затем в формулу пути подставить полученное выражение вместо времени t.

Видео:РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ физика 9 ПерышкинСкачать

Выражаем время из формулы для скорости

Выпишем формулу, связывающую начальную и конечную скорость тела:

[ large v = v_ + a cdot t ]

Избавимся в правой части от начальной скорости, обозначенной символом ( v_). Для этого из обеих частей уравнения вычтем число ( v_). Получим такую запись:

[ large v — v_ = a cdot t ]

Теперь, чтобы справа в формуле оставалось только время «t», избавимся от ускорения «a». Для этого разделим обе части уравнения на «a»:

Это выражение нам пригодится для дальнейшего вывода формулы «путь без времени».

Видео:Уравнение равномерного прямолинейного движения | Физика 10 класс #3 | ИнфоурокСкачать

В формулу пути подставим выражение для времени

Запишем теперь формулу для пути S и полученную формулу для времени t, объединив их в систему:

В первом уравнении системы будем заменять символ t дробью из второго уравнения. Тогда система из двух уравнений превратится в единственное уравнение. И в этом уравнении не будет символа t времени:

Осталось теперь упростить полученное выражение. Будем производить упрощение по частям.

Упрощаем выражение, расположенное до знака «плюс» в правой части

Выпишем отдельно все, что располагается до знака «плюс» в правой части уравнения:

Умножим числитель дроби на число (v_).

сначала числитель обособим скобками;
затем запишем число (v_) перед скобками;
а потом внесем это число внутрь скобок.

В числитель дроби, обособленный с помощью скобок помещаем число (v_):

Теперь необходимо умножить скобку на число (v_). На рисунке 2 указано, как правильно выражение в скобках умножить на число, стоящее за скобками.

Нужно к каждой скорости в скобках дописать число (v_), умножая его на эти скорости. Получим такое выражение:

То есть, вместо первоначальной записи, мы получили такую запись:

Возводим в квадрат дробь

После знака «плюс» в правой части уравнения располагается дробь, которую нужно возвести в квадрат. Обратим внимание на эту дробь:

Правильно возвести дробь в степень поможет рисунок 3.

В результате возведения в квадрат дробь приобретет такой вид:

В числителе этой дроби находится выражение в скобках, которое нужно возвести в квадрат. И нам придется применить одну из формул сокращенного умножения. Запоминать формулы сокращенного умножения удобно в виде, приведенном на рисунке 4.

Используем для этого формулу сокращенного умножения, которая содержит знак «минус». Она называется «Квадрат разности». Тогда числитель дроби превратится в такую запись:

Теперь можем записать полученную дробь:

Упрощаем правую часть, записанную после знака «плюс»

Обратим внимание на все, что располагается в правой части уравнения после знака «плюс»:

Мы уже провели некоторые преобразования и можем теперь заменить дробь, возводимую в квадрат более подробной записью:

Примечание: Когда мы умножаем одну дробь на другую, то можем менять местами знаменатели этих дробей.

Итак, поменяем местами знаменатели дробей:

Теперь видно, что мы можем сократить ускорение и еще немного упростить выражение:

А перемножив числители и знаменатели двух дробей, получим такую запись:

Теперь, первоначальную дробь можно заменить дробью, полученной в ходе преобразований:

Мы закончили преобразовывать выражения, содержащиеся в правой части уравнения после знака «плюс».

Теперь, осталось сложить две дроби в правой части – дробь, записанную до знака «плюс» с дробью, записанной после знака «плюс». А чтобы эти дроби можно было сложить, нужно будет привести их к общему знаменателю.

Приводим к общему знаменателю дроби в правой части уравнения

Вернемся еще раз к первоначальному уравнению:

Заменим правую часть этого уравнения выражениями, которые мы получили:

Сравним знаменатели дробей.

Первая дробь обладает знаменателем «a», а вторая – «2a». Выберем число «2a» в качестве общего знаменателя обеих дробей.

Чтобы первую дробь привести к общему знаменателю «2a», умножим ее на единицу:

Примечания:

Нам известно, что если какое-либо число умножить на единицу, то после умножения это число не изменится. Значит, если какое-либо выражение умножить на единицу, то полученное выражение останется равным самому себе. На единицу можно умножать все, что угодно – дроби, выражения в скобках и т. п.
Математики часто применяют прием умножения на единицу. А после этого единицу записывают в виде некоторой дроби. При этом используют правило: Единица – это дробь, у которой числитель и знаменатель равны (одинаковые).

Так как снизу в первой дроби не хватает числа 2, то единицу представим в виде дроби 2/2:

Получим такую дробь:

Поместим ее в выражение для пути:

Дроби с одинаковыми знаменателями складываем

Теперь знаменатели дробей равны. И мы можем записать эти дроби под общим знаменателем:

Раскроем скобки в числителе полученного выражения:

Примечание: Обратим внимание на то, что в числителе дважды встречается член (2v_ v), обладающий различными знаками. В начале числителя – знаком «плюс», а в конце числителя – знаком «минус». Это означает, что из числа (2v_v) вычитается такое же число (2vv_). В конце концов, это число покидает нашу запись и, она упрощается:

Перепишем выражение, записав все, что содержит знак «плюс» в начало числителя:

Вычтем подобные члены, содержащие ( v^_):

В результате получим короткую запись. Именно о ней говорят, когда имеется ввиду формула пути без времени:

Примечания:

Это формула, с помощью которой можно рассчитать путь тела, когда известны его начальная и конечная скорость, а, так же, ускорение.
Видно, что время t в правой части этого выражения отсутствует.
Мы выводили эту формулу для случая, когда тело увеличивало скорость.

Видео:Равноускоренное движение. Вывод формулСкачать

Как выглядит формула пути без времени, когда скорость тела уменьшается

Если скорость тела будет уменьшаться, формулу для вычисления пути нужно будет переписать в таком виде:

Получить такую формулу можно, проделав все шаги, описанные выше. Попробуйте самостоятельно ее получить. Выводить формулу нужно, используя формулы для уменьшающейся скорости:

Видео:Скорость и перемещение при прямолинейном равноускоренном движении. 9 класс.Скачать

Выводы

Пусть нам известны начальная и конечная скорость тела и его ускорение. Тогда путь, пройденный телом, можно рассчитать так:

Видео:Прямолинейное равнопеременное движение, ускорение. 9 класс.Скачать

Прямолинейное равнопеременное движение

Прямолинейное равнопеременное движение — движение тела вдоль прямой, характеризующееся постоянным по модулю и направлению линейным ускорением.

Траектория такого движения — прямая, поэтому в задачах равнозначными являются понятия пути и модуля перемещения. Такое движение может быть описано несколькими соотношениями:

вектор скорости тела при равнопеременном движении

где
- — вектор конечной скорости движения
- — вектор начальной скорости движения
- — вектор ускорения
- — время движения
вектор перемещения тела при равнопеременном движении

Однако это векторные уравнения, с которыми работать достаточно сложно, а иногда, просто не хочется. Попробуем, анализируя условия задачи, составить уравнения скалярного вида, спроецировав вектора на некую ось.

Рис. 1. Равноускоренное движение 1

Пример 1. Тело движется прямо с начальной скоростью и ускоряется. По задаче выставляем вектора на ось OX (движение прямолинейное) (рис. 1). Сказано, что тело движется вдоль оси (вектор направлен по оси) и ускоряется (вектор также направлен вдоль оси). Осталось зафиксированные вектора спроецировать:

Для уравнения (1):
Для уравнения (2):

В общем случае, мы не можем предугадать направления векторов и , соответственно, мы не можем указать точный знак проекции этих векторов на выбранную ось. Но не заморачиваемся: в результате решения задачи мы получим одно и то же по модулю число, даже если ошибёмся. Т.е. выбираем направления как хотим, а потом анализируем ответ.

Рис. 2. Равноускоренное движение-2

Пример 2. Тело движется в положительном направлении оси и затормаживает. По задаче тело движется вдоль оси (вектор направлен по оси), а торможение говорит о том, что вектор ускорения ( ) направлен против оси OX (рис. 2). Проецируем:

Для уравнения (1):
Для уравнения (2):

Рис. 3. Равноускоренное движение-3

Пример 3. Тело движется в отрицательном направлении оси и затормаживает. По задаче тело движется в обратную сторону оси OX (вектор направлен против оси), а торможение говорит о том, что вектор ускорения ( ) направлен против движения, а значит, по оси OX (рис. 3). Проецируем:

Для уравнения (1):
Для уравнения (2):

Рис. 4. Равноускоренное движение-4

Пример 4. Тело движется в отрицательном направлении оси и ускоряется. По задаче тело движется в обратную сторону оси OX (вектор направлен против оси), а ускорение говорит о том, что вектор ускорения ( ) направлен в сторону движения, а значит, против оси OX (рис. 4). Проецируем:

Для уравнения (1):
Для уравнения (2):

Вывод: только что мы получили восемь различных формул, применимых для решения задач. Очень не хотелось бы их помнить. К счастью, есть выход: запомнить и понять векторный вид этих уравнений (1) и (2), а далее, применительно к данной вам задаче, просто адаптировать их, используя проекции.

Кроме формул (1) и (2), имеется ещё одна расчётная формула, которая чаще всего используется, когда в задаче на нужно найти время или его не дано. Воспользуемся уже имеющимися (1) и (2), считая движение тела равноускоренным. Выделим из (1) время:

Подставим (3) в (2) при условии :

Таким образом, мы получили формулу, в которой нет параметра времени.