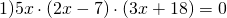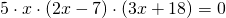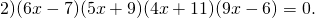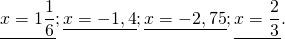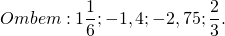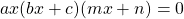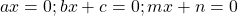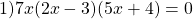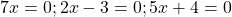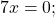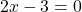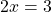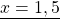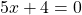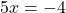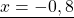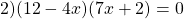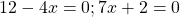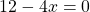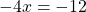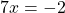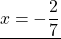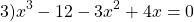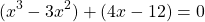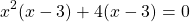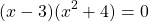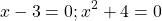Уравнение равно нулю тогда и только тогда (4 видео)

Произведение равно нулю

В каком случае произведение равно нулю?

произведение равно нулю, если хотя бы один из множителей равен нулю .

С помощью этого правила решают уравнения, в которых произведение нескольких множителей равно нулю. Уравнения вида «Произведение равно нулю» — одни из самых распространенных в математике. Их начинают изучать с 6 класса. В 6 классе множители представляют собой линейные уравнения.

Это уравнение вида «произведение равно нулю». Произведение равно нулю, если хотя бы один из множителей равен нулю, поэтому приравниваем к нулю каждый из множителей:

5x=0 или 2x-7=0 или 3x+18=0.

Теперь решаем каждое из уравнений. Первое — простейшее линейное уравнение. Обе части уравнения делим на число, стоящее перед иксом:

Второе и третье — линейные уравнения. Алгоритм решения: неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:

2x=7 I :2 3x=-18 I :3

Замечания.

1) Это уравнение также можно рассмотреть как произведение четырех множителей:

Рассуждаем так: поскольку произведение равно нулю, если хотя бы один из множителей равен нулю, а первый множитель 5≠0, приравниваем к нулю остальные множители:

x=0 или 2x-7=0 или 3x+18=0.

2) Поскольку перед буквой и перед скобками знак умножения можно не писать, условие уравнений обычно выглядят так:

Это уравнение типа «произведение равно нулю». Произведение равно нулю, если хотя бы один из множителей равен нулю. Приравниваем к нулю каждый из множителей:

6x-7=o или 5x+9=0 или 4x+11=0 или 9x-6=0

6x=7 I:6 5x=-9 I:5 4x=-11 I:4 9x=6 I:9

x=7/6 x=-9/5 x=-11/4 x=6/9

В первом уравнении получили неправильную дробь. Выделяем из нее целую часть. Во втором и третьем уравнении ответ записываем в виде десятичной дроби. Для этого делим числитель на знаменатель уголком. В четвертом уравнении нужно сократить дробь в ответе

А как узнать, записать ответ в виде обыкновенной или в виде десятичной дроби? Любую ли обыкновенную дробь можно перевести в десятичную? Любую ли десятичную дробь можно перевести в обыкновенную? Об этом мы поговорим в следующий раз.

Содержание

2 Comments
Уравнения равные нулю
13 комментариев
Неполные квадратные уравнения
теория по математике 📈 уравнения
Неполное квадратное уравнение при b=0: ax 2 +c=0
Неполное квадратное уравнение при с=0: ax 2 +bx=0
Неполное квадратное уравнение с коэффициентами b и с равными нулю: ax 2 =0
🔥 Видео

Видео:Уравнение в котором произведение множителей равно нулю. Алгебра 7 класс.Скачать

2 Comments

определение наверху неверное, т.к. произведение двух или более множителей равно нулю тогда и только тогда когда хотя-бы один из них равен нулю, а остальные не теряют смысла.

Мне понравился ход мысли Вашего учителя математики. Она расширила определение, чтобы ученики не забывали проверить, входят ли найденные корни в область допустимых значений уравнения (или неравенства).

Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Уравнения равные нулю

Что такое «уравнения равные нулю»?

Если в левой части уравнения стоит сумма или разность одночленов или многочленов, а в правой части — нуль, то это может быть обычное линейное уравнение.

Если левая часть уравнения представляет собой произведения двух или нескольких множителей, а правая часть — нуль, то это — уравнение типа «произведение равно нулю».

В общем виде простейшие равные нулю уравнения можно записать как

(множителей может быть больше).

Произведение равно нулю, если хотя бы один из множителей равен нулю. Поэтому приравниваем к нулю каждый множитель:

и решаем каждое из полученных уравнений отдельно.

Это — уравнение типа «произведение равно нулю».

Произведение равно нулю, если хотя бы один из множителей равен нулю. Приравниваем к нулю каждый из множителей:

Если в уравнении, равном 0, левую часть можно разложить на множители, то такое уравнение также можно решить как уравнение типа «произведение равно 0».

Сгруппируем первое слагаемое с третьим, а четвёртое — со вторым:

Из первых скобок вынесем за скобки общий множитель x², из вторых — 4:

Общий множитель (x-3) вынесем за скобки:

Получили уравнение типа «произведение равно 0». Приравниваем к нулю каждый из множителей:

Корень первого уравнения —

Второе уравнение не имеет корней (сумма положительных чисел не может равняться нулю).

В алгебре многие уравнения сводятся к уравнениям типа «произведение равно нулю» с помощью разложения на множители.

Множители могут линейными, квадратными, логарифмическими, тригонометрическими и т.д. уравнениями.

Еще один важный частный случай уравнений, равных нулю, рассмотрим позже.

13 комментариев

Показательное уравнение:
3^((x+2)/(3x-4))-2*3^((5x-10)/(3x-4))-7=0
Корень известен: x=2.
Подскажите, пожалуйста, как найти решение. Преобразовать в квадратное уравнение что-то не получается.

Видео:1 Как решать уравнения всех видов Решите уравнение Виды уравнений МАТЕМАТИКА ОНЛАЙНСкачать

Неполные квадратные уравнения

теория по математике 📈 уравнения

Квадратным уравнением называется уравнение вида ax 2 +bx+c=0, где х – переменная, a, b, c некоторые числа, причем a≠0. Обычно его называют полным квадратным уравнением.

Если в таком уравнении один из коэффициентов b или c равен нулю, либо оба одновременно равны нулю, то такое уравнение называется неполным квадратным уравнением.

Неполное квадратное уравнение при b=0: ax 2 +c=0

Для решения такого вида уравнения надо выполнить перенос коэффициента с в правую часть, затем найти квадрат переменной (делим обе части на одно и то же число), найти два корня уравнения, либо доказать, что корней нет (если х 2 равен отрицательному коэффициенту; знаем, что квадрат любого числа равен только положительному числу).

Пример №1. Решить уравнение:

Выполним перенос числа –45 в правую часть, изменяя знак на противоположный: 5х 2 =45; найдем переменную в квадрате, поделив обе части уравнения на 5: х 2 =9. Видим, что квадрат переменной равен положительному числу, поэтому уравнение имеет два корня, находим их устно, извлекая квадратный корень из числа 9, получим –3 и 3. Оформляем решение уравнения обычным способом:

Ответ: х=±3 или можно записать ответ так: х₁=–3, х₂=3 (обычно меньший корень записывают первым). Пример №2. Решить уравнение:

Выполним решение уже известным способом: –6х 2 =90. х 2 =–15 Здесь видим, что квадрат переменной равен отрицательному числу, а это значит, что уравнение не имеет корней. Ответ: нет корней. Пример №3. Решить уравнение:

Здесь мы видим в левой части уравнения формулу сокращенного умножения (разность квадратов двух выражений). Поэтому, можем разложить данное выражение на множители, и найти корни уравнения: (х–10)(х+10)=0. Соответственно, вспомним, что произведение двух множителей равно нулю тогда, когда хотя бы один из множителей равен нулю, то есть х–10=0 или х+10=0. Откуда имеем два корня х₁=10, х₂=–10.

Неполное квадратное уравнение при с=0: ax 2 +bx=0

Данного вида уравнение решается способом разложения на множители – вынесением за скобки переменной. Данное уравнение всегда имеет два корня, один из которых равен нулю. Рассмотрим данный способ на примерах.

Пример №4. Решить уравнение:

Выносим переменную х за скобки: х(х+8)=0. Получаем два уравнения х=0 или х+8=0. Отсюда данное уравнение имеет два корня – это 0 и –8.

Пример №5. Решить уравнение:

Здесь кроме переменной можно вынести за скобки еще и коэффициент 3, который является общим множителем для данных в уравнении коэффициентов. Получим: 3х(х–4)=0. Получаем два уравнения 3х=0 и х–4=0. Соответственно и два корня – нуль и 4.