Трехшарнирной аркой называется криволинейный брус, имеющий на оси три шарнира.
Если каждая полуарка состоит из ломанных участков, такая система называется трех шарнирной рамой.
Выпуклость арочных систем, в отличии от висячих, направленно против действия внешней нагрузки.
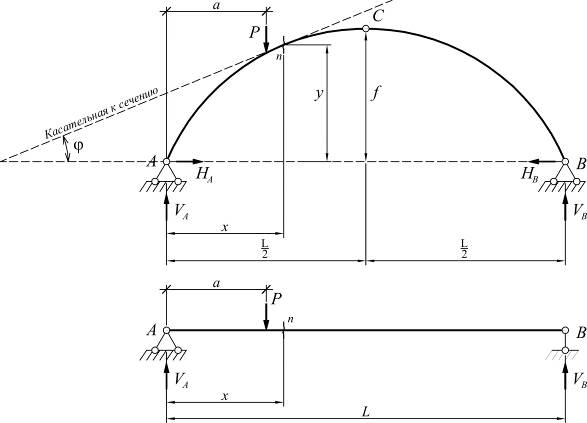
Расстояние между центрами опорных шарниров L называется пролетом арки, а расстояние от среднего шарнира до прямой, соединяющей опорные шарниры ƒ – стрелой подъема арки.
Трехшарнирные арки являются распорными системами, т. к. от вертикальных нагрузок возникают горизонтальные составляющие опорных реакций.
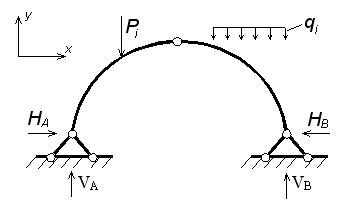
Реакции опор трехшарнирной системы характеризуются каждая двумя параметрами: вертикальной и горизонтальной составляющей опорной реакции. Они могут быть определены из трех уровней статики и четвертого уравнения, выражающего равенство нулю момента всех сил, действующих на левую или правую часть системы, относительно шарнира С. Следовательно трехшарнирная система является статически определимой.
При действии на трехшарнирную систему вертикальной нагрузки, горизонтальные составляющие На и Нв реакций опор, называемые распором, равны между собой.
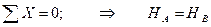
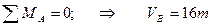
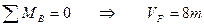
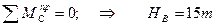
Определение внутренних усилий в трехшарнирной арке
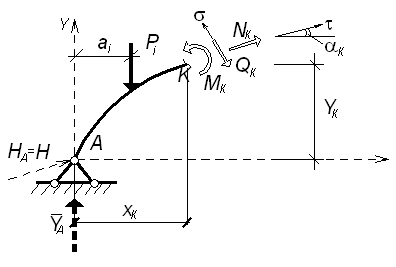
В поперечных сечениях арки возникают изгибающие моменты М, поперечные силы Q и продольные силы N.
При определении внутренних усилий в сечениях арки используют такое же правило знаков, как и для балок.
| .I. | 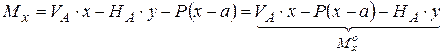 Для балки: Для балки: 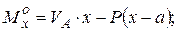
| (1) | ||||||
| II. | 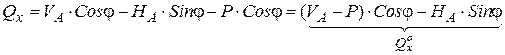 Для балки: Для балки: 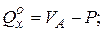
| (2) | ||||||
| III. | 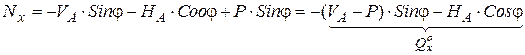
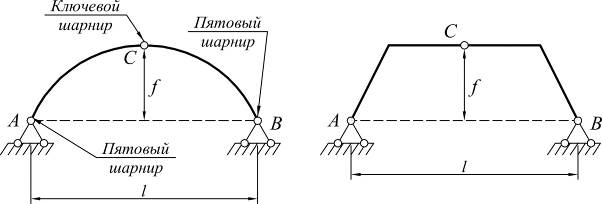
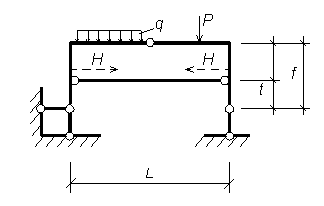
В выражениях (1), (2), (3) принято: М º х, Q º х балочный момент и балочная поперечная сила в рассматриваемом сечении (см. рис. б). Рациональное очертание оси арки Наиболее рационально материал арки используется в том случае, когда изгибающий момент в любом сечении арки = 0. Содержание Видео:Трехшарнирная арка. Определение усилий M,Q,N в обозначенных сечениях аналитическим методомСкачать  iSopromat.ruРассмотрим общий порядок расчета внутренних силовых факторов в трехшарнирных системах. Решение традиционно начинается с расчета реакций в опорах. Видео:Рациональные уравнения. ОГЭ номер 21 | ЕГЭ номер 13 | Математика | TutorOnlineСкачать  Определение реакций опорПри действии внешней нагрузки (сосредоточенных сил Рi, и распределенных нагрузок qi) на трехшарнирные системы, в каждой из опор возникают по две реакции: вертикальные — VA (YA), VB (YB) и горизонтальные (распор) – НA(XA), НB(XВ) (рисунок 3.27). Определение опорных реакций в таких системах производится с помощью составления уравнений равновесия. Рисунок 3.27 – Трехшарнирная арка Наряду с тремя основными уравнениями статики для всей системы: необходимо записать четвертое уравнение, выражающее условие равенства нулю изгибающего момента Мс в замковом шарнире «С»: Определение опорных реакций таким способом довольно затруднительно, так как в ряде случаев приходится решать систему из четырех линейных уравнений. При действии на трехшарнирную конструкцию только обычной вертикальной нагрузки, определение опорных реакций несколько упрощается. Рассмотрим определение опорных реакций при действии только вертикальной нагрузки на примере трехшарнирной арки. Арка с опорными шарнирами, расположенными на одном уровнеРисунок 3.28 – Пример расчета трехшарнирной арки Для определения опорных реакций VA, VB, НA, НB в арке составим упомянутые выше уравнения равновесия: Получаем, что выражение для опорной реакции VB в арке совпадает с аналогичным выражением в балке на двух шарнирных опорах того же пролета загруженной той же вертикальной нагрузкой. Воспользуемся нулевым индексом для обозначения величин, характеризующих эту простую балку. 2) Опорную реакцию VA можно определить из условия ∑Yi= 0 Делаем такой же вывод: определение VB аналогично определению VB°. При действии лишь вертикальной нагрузки Рi, горизонтальные опорные реакции (распор) равны между собой. 3) Для определения величины распора Н от действия внешней нагрузки составим четвертое уравнение: Построим для приведенной схемы простой балки эпюру М, на которой величина момента под шарниром «С» равна: Следовательно, последнее уравнение равновесия, выраженное через момент М, будет иметь вид: Мc 0 −H×f = 0, H = Мc 0 / f. Таким образом: величина распора арки (рамы) при действии вертикальной нагрузки равна балочному моменту в сечении под замковым шарниром «С», уменьшенному в f раз. Полученная формула справедлива при действии вертикальных сосредоточенных сил и распределенных нагрузок, как в арках, так и в трехшарнирных рамах. Если трехшарнирная система имеет приподнятую затяжку, то претерпевает изменение только знаменатель: где t — расстояние от оси затяжки до линии, соединяющей опорные шарниры (рисунок 3.29) Рисунок 3.29 – Трехшарнирная рама с затяжкой Видео:Рациональная форма аркиСкачать  Расчет внутренних усилийОпределим величину и направление внутренних силовых факторов в трехшарнирной арке при действии вертикальной нагрузки Для составления выражений внутренних усилий в трехшарнирной арке рассмотрим равновесие ее отсеченной части, расположенной слева от сечения. а) Выражение для изгибающего момента Мк Рисунок 3.30 – Отсеченная левая часть арки τ − ось, касательная к очертанию арки в точке «К»; σ- ось, перпендикулярная к оси в точке «К»; М, Q, N — внутренние усилия, направленные согласно соответствующим правилам знаков. Составим уравнение равновесия для отсеченной части относительно точки «К»: Выделяя из этого уравнения Мк и учитывая, что: Анализируя это выражение можно заметить, что арочные системы рациональнее балочных, вследствие некоторого уменьшения величины балочного момента М за счет возникающего распора Н. б) Выражение для поперечной силы Qк Для отсеченной части составим сумму проекций всех сил на ось: Выделяя Qк, с учетом того, что VA − Рi = Qк о , окончательно получим: Для отсеченной части составим сумму проекций всех сил на ось: Выделяя Nк, с учетом того, что VA − Рi = Qк о , окончательно получим: Видео:Лекция Zoom. Расчет трехшарнирных арок. Палагушкин В.ИСкачать  Рациональное очертание для трехшарнирной аркиРациональным очертанием оси арки является такое, при котором момент в любом ее сечении равен нулю. Так в предыдущем пункте, при действии вертикальной нагрузки, нами было получено следующее выражение для момента: Мк= Мк o − H × yк Положив это выражение равным нулю и выделяя выражение для ординаты yк, будем иметь: Анализ полученной формулы показывает: − уравнение рациональной оси арки определяется видом нагрузки; − при вертикальной нагрузке ось арки будет рациональной, если ее очертание меняется по закону изменения балочного момента. Рассмотрим пример по определению рационального очертания арки, загруженной по длине равномерно распределенной нагрузкой. Для произвольного сечения «К» с координатами yк, xк имеем: yк = Мк o / Н Рассматривая равновесие по моментам левой отсеченной части, получим: М (x) = q × L × x/ 2 − q × x 2 / 2 Рисунок 3.31 – Определение рационального очертания оси арки Таким образом, рациональной осью для арки, загруженной равномерно распределенной нагрузкой по всему пролету является квадратная парабола. Это объясняется тем, что постоянная нагрузка на арку и ее собственный вес составляют большую долю от общей нагрузки. Как известно, эти виды нагрузок близки к равномерно распределенным. Уважаемые студенты! Видео:Арка. Эпюры M, Q, NСкачать  Изгибающие моменты в сечениях арокТрехшарнирные системы Трехшарнирная система состоит из двух дисков, соединенных между собой шарниром (С) и прикрепленных шарнирами (А и В) к земле. Если диски I и II представляют собой криволинейные брусья, то такая система называется трехшарнирной аркой. Если дисками I и II являются ломаные стержни, то система называется трехшарнирной рамой. Шарниры А и В называются опорными или пятовыми шарнирами, С — ключевой шарнир. Расстояние между опорными шарнирами АВ по горизонтали называется пролетом арки или рамы. Расстояние от ключа до линии, соединяющей опорные шарниры, называется стрелой подъема арки f. Если Трехшарнирные системы являются статически определимыми системами, так как : W = 3D — 2Ш0 — Соп = 3·2 — 2·1 — 4 = 0 и геометрически неизменяемыми. Трехшарнирные системы — это распорные системы, так как в их опорах, даже при отсутствии вертикальной нагрузки, возникают горизонтальные составляющие опорных реакций. Для определения опорных реакций мы можем составить три уравнения статики, а наличие ключевого шарнира С позволяет составить дополнительное уравнение: и определить все четыре опорные реакции. Трехшарнирные системы могут быть симметричными и несимметричными Опорные шарниры А и В могут располагаться в одном уровне (рис.3) и могут располагаться в разных уровнях (рис.4) — такие системы называются ползучими арками или рамами.
В практике часто встречаются системы, у которых распор воспринимается затяжкой:
арка с затяжкой арка с повышенной затяжкой Если каждая полуарка выполнена в виде фермы, то такая система называется сквозной аркой или трехшарнирной фермой.
Сплошные трехшарнирные арки. Определение опорных реакций.
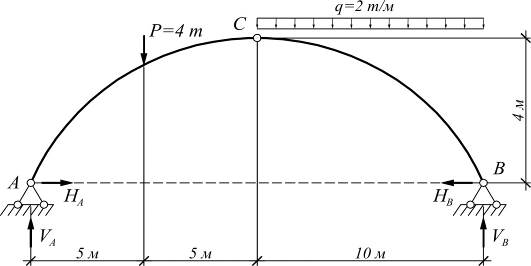
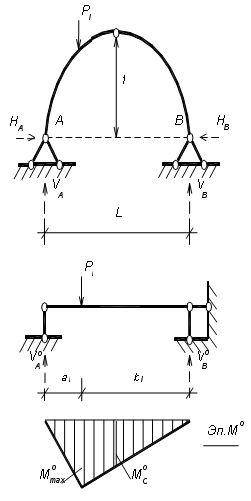
При действии на арку внешней нагрузки, в каждой ее опоре возникают по две реакции: горизонтальная и вертикальная. Для определения всех опорных реакций мы можем записать для плоской системы три уравнения статики и для трехшарнирной арки можно составить четвертое уравнение, приравняв к нулю сумму моментов правых либо левых сил относительно шарнира С. Следовательно реакции определяются: 1) вертикальные реакции Следовательно, вертикальные составляющие опорных реакций трехшарнирных систем, равны балочным. 2) горизонтальные реакции Если на трехшарнирную арку действует только вертикальная нагрузка, то распоры равны между собой Чем больше стрела подъема арки, тем меньше распор. Определение внутренних усилий в сечениях трехшарнирной арки Внутренними усилиями, возникающими в поперечных стержнях арки, являются изгибающие моменты М, поперечные силы Q и продольные силы N.
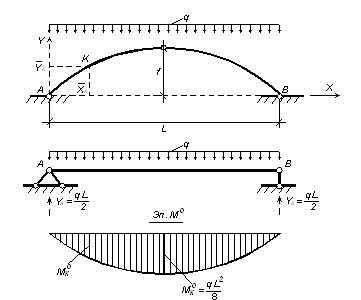
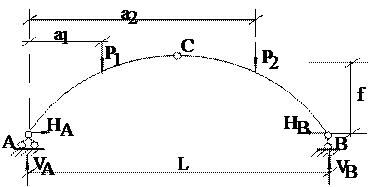
Изгибающие моменты в сечениях арок Определим М в сечении I-I Тогда изгибающий момент в любом сечении балки определяется Из выражения (1) следует, что моменты в сечениях арки меньше моментов в соответствующих сечениях балки, следовательно, арка экономичнее балки и аркой можно перекрыть пролет гораздо больше, чем балкой. Для определенного вида нагрузки можно подобрать такое очертание оси арки, что изгибающий момент М в любом сечении арки будет равен нулю. Такие арки называются арками с рациональным очертанием оси. Мх = Пусть трехшарнирная арка загружена равномерно распределенной нагрузкой по всему пролету. Тогда 🎥 ВидеоРасчет трехшарнирной арки. Определение усилий в сеченииСкачать  С.М. Задача №3.1 Трёхшарнирная арка параболического очертанияСкачать  ЭТО НУЖНО ЗНАТЬ — Как решать Дробно Рациональные уравнения?Скачать  Построение эпюр в аркахСкачать  Прогиб консоли (2). Уравнение осиСкачать  Арка статически неопределимаяСкачать  Арки Виды арок, усилия в арках / строительная механикаСкачать  Математика 6 класс (Урок№48 - Изображение рациональных чисел на координатной оси.)Скачать  Расчёт трехшарнирных систем. Арка. Нахождение внутренних усилий в отмеченных сечениях 1 и 2. Часть 1Скачать  Расчет трехшарнирной арки в MathCAD, Scad, LiraSapr, SolidWorksСкачать  С.М. Задача №3.2 аналитический расчёт круговой аркиСкачать  Задача про арку Как рассчитать высоту опор арочного мостаСкачать  Трехшарнирная арка. Нахождение усилий M,Q,N в обозначенных сечениях с помощью линий влиянияСкачать  Метод сеченийСкачать  №534. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу в 120Скачать  |
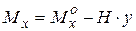
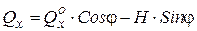
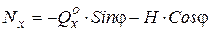

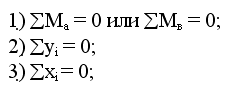
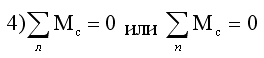
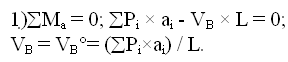


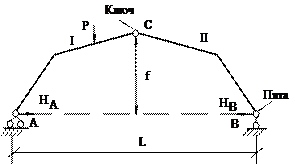 1) 2)
1) 2) — пологие арки
— пологие арки — повышенные арки
— повышенные арки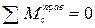 или
или 
 3)
3)





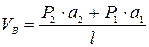

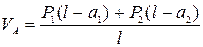


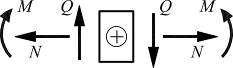
 Правило знаков
Правило знаков

 Мх =
Мх =  Уравнение оси арки рационального очертания.
Уравнение оси арки рационального очертания.

 Пример.
Пример.



 — уравнение квадратной параболы.
— уравнение квадратной параболы.