С помощю этого онлайн калькулятора можно найти расстояние от точки до прямой. Дается подробное решение с пояснениями. Для вычисления расстояния от точки до прямой, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), введите координаты точки и элементы уравнения в ячейки и нажимайте на кнопку «Решить».
- Предупреждение
- Расстояние от точки до прямой − теория, примеры и решения
- 1. Расстояние от точки до прямой на плоскости
- 2. Расстояние от точки до прямой в пространстве
- Онлайн калькулятор. Расстояние от точки до прямой в пространстве
- Найти расстояние между точкой и прямой в пространстве
- Ввод данных в калькулятор для вычисления расстояния между точкой и прямой в пространстве
- Дополнительные возможности калькулятора вычисления расстояния между точкой и прямой в пространстве
- Теория. Расстояние между точкой и прямой в пространстве
- Расстояние от точки до прямой в пространстве: онлайн-калькулятор
- Материалы, которые помогут вам лучше разобраться в теме:
- Как найти расстояние от прямой до точки в пространстве. Онлайн-калькулятор
- Почему калькуляторы на нашем сайте часто используют:
- 🔥 Видео
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Расстояние от точки до прямой | Вывод формулы через Подобие и ПифагораСкачать

Расстояние от точки до прямой − теория, примеры и решения
Рассмотрим эту задачу в двухмерном и трехмерном пространствах.
1. Расстояние от точки до прямой на плоскости
Пусть в двухмерном пространстве задана точка M0(x0, y0) и прямая L:
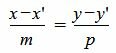 , , | (1) |
где q=(m,p) направляющий вектор прямой L.
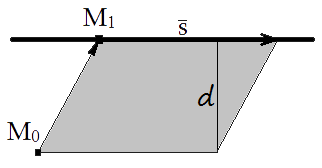
Найдем расстояние от точки M0 до прямой (1)(Рис.1).
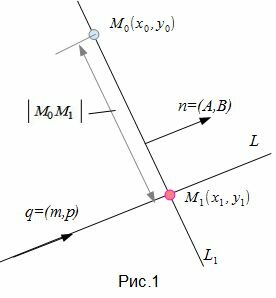 |
Алгоритм нахождения расстояния от точки M0 до прямой L содержит следующие шаги:
- построить прямую L1, проходящую через точку M0 и перпендикулярную прямой L,
- найти пересечение прямых L и L1(точка M1)
- найти найти расстояние между точками M0 и M1.
Уравнение прямой, проходящей через точку M0(x0, y0) имеет следующий вид:
| A(x−x0)+B(y−y0)=0 | (2) |
Как видно из рисунка Рис.1, для того, чтобы прямая L1 была перпендикулярна прямой L нужно , чтобы направляющий вектор q прямой L была коллинеарна нормальному вектору n прямой L1, поэтому в качестве нормального вектора прямой L1 достаточно взять направляющий вектор прямой L. Тогда уравнение прямой L1, представленной уравнением (2) можно записать так:
| m(x−x0)+p(y−y0)=0 | (3) |
| mx+py−mx0−py0=0 | (4) |
Для нахождения точки пересечения прямых L и L1, которая и будет проекцией точки M0 на прямую L, можно решить систему из двух уравнений (1) и (3) с двумя неизвестными x и y. Выражая неизвестную x из одного уравнения и подставляя в другое уравнение получим координаты точки M1(x1, y1).
Найдем точку пересечения прямых L и L1 другим методом.
Выведем параметрическое уравнение прямой (1):
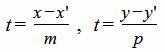 |
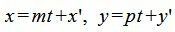 | (5) |
Подставим значения x и y в (4):
| m(mt+x’)+p(pt+y’)−mx0−py0=0 |
| m 2 t+mx’+p 2 t+py’−mx0−py0=0 |
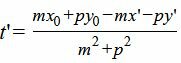 | (6) |
Мы нашли такое значение t=t’, при котором координаты x и y точки на прямой L удовлетворяют уравнению прямой L1(4). Следовательно, подставляя значение t’ в (5) получим координаты проекции точки M0 на прямую L:
Далее находим расстояние между точками M0 и M1 используя формулу:
 . . | (7) |
Пример 1. Найти расстояние от точки M0(−6, 2) до прямой
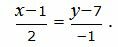 | (8) |
Направляющий вектор прямой (8) имеет вид:
Т.е. m=2, p=−1. Из уравнения прямой (8) видно, что она проходит через точку M’ (x’, y’)=(1, 7)(в этом легко убедится − подставляя эти значения в (8) получим тождество 0=0), т.е. x’=1, y’=7. Подставим значения m, p, x0, y0, x’, y’ в (6):
 |
 |
 , , |
Подставляя значение t в (5), получим:
 |
Вычислим расстояние между точками M0(-6, 2) и M1
 |
Упростим и решим:
  |
Расстояние от точки M0(-6, 2) до прямой (8) :
 |
2. Расстояние от точки до прямой в пространстве
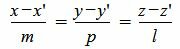 , , | (9) |
где q=(m, p, l) направляющий вектор прямой L.
Найдем расстояние от точки M0 до прямой (9)(Рис.2).
 |
Алгоритм нахождения расстояния от точки до прямой L содержит следующие шаги:
- построить плоскость α, проходящую через точку M0 и перпендикулярную прямой L,
- найти пересечение плоскости α и прямой L(точка M1)
- найти расстояние между точками M0 и M1.
| A(x−x0)+B(y−y0)+C(z−z0)=0 | (10) |
где n=(A,B,C) нормальный вектор плоскости α.
Как видно из рисунка Рис.2, для того, чтобы плоскость α была перпендикулярна прямой L нужно , чтобы направляющий вектор q прямой L была коллинеарна нормальному вектору n плоскости α, поэтому в качестве нормального вектора плоскости α достаточно взять направляющий вектор прямой L. Тогда уравнение плоскости α, представленной уравнением (10) можно записать так:
| m(x−x0)+p(y−y0)+l(z−z0)=0 |
| mx+py+lz−mx0−py0−lz0=0 | (11) |
Для нахождения точки пересечения плоскости α и прямой L, которая и будет проекцией точки M0 на прямую L, выведем параметрическое уравнение прямой (9):
 |
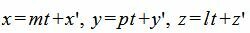 | (12) |
Подставим значения x и y в (11):
| m(mt+x’)+p(pt+y’)+l(lt+z’)−mx0−py0−lz0=0 |
| m 2 t+mx’+p 2 t+py’+l 2 t+ly’−mx0−py0−lz0=0 |
 | (13) |
Мы нашли такое значение t=t’, при котором координаты x,y и z точки на прямой L удовлетворяют уравнению плоскости (11). Следовательно, подставляя значение t’ в (12) получим координаты проекции точки M0 на прямую L:
| M1(x1, y1, , z1), |
Далее вычисляем расстояние между точками M0 и M1 используя формулу
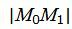 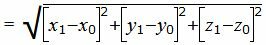 , , | (14) |
которое является расстоянием между точкой M0 и прямой (9).
Пример 2. Найти расстояние от точки M0(1, 2, 1) до прямой
 | (15) |
Направляющий вектор прямой (15) имеет вид:
Т.е. m=2, p=4, l=−6. Из уравнения прямой (15) видно, что она проходит через точку M’ (x’, y’, z’)=(4, 3, 1)(в этом легко убедится − подставляя эти значения в (15) получим тождество 0=0=0), т.е. x’=4, y’=3, z’=1. Подставим значения m, p, l x0, y0, z0 x’, y’, z’ в (13):
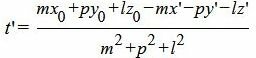 |
 |
 |
Подставляя значение t=t’ в (12), получим координаты точки M1:
 , , |
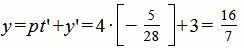 , , |
 . . |
Далее, используя формулу (14) вычисляем расстояние от точки M0 до прямой (15):
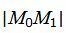 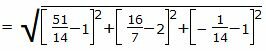 . . |
Упростим и решим:
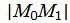   . . |
Расстояние от точки M0(1, 2, 1) до прямой (15) :
Видео:18. Расстояние от точки до прямой в пространствеСкачать

Онлайн калькулятор. Расстояние от точки до прямой в пространстве
Используя этот онлайн калькулятор, вы сможете найти расстояния между точкой и прямой в пространстве.
Воспользовавшись онлайн калькулятором, вы получите детальное пошаговое решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление расстояния от точки до прямой в пространстве и закрепить пройденный материал.
Видео:Расстояние от точки до прямойСкачать

Найти расстояние между точкой и прямой в пространстве
Ввод данных в калькулятор для вычисления расстояния между точкой и прямой в пространстве
В онлайн калькулятор можно вводить числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора вычисления расстояния между точкой и прямой в пространстве
- Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.
Теория. Расстояние между точкой и прямой в пространстве
Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.
Если в пространстве заданы координаты точки M0( x 0, y 0, z 0) и известны s = — направляющий вектор прямой l , M1( x 1, y 1, z 1) — координаты точки лежащей на l , то можно найти расстояние от точки M0( x 0, y 0, z 0) до прямой l , используя формулу
| d = | | M0M1 × s | |
| | s | |
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Видео:Видеоурок "Расстояние от точки до прямой"Скачать

Расстояние от точки до прямой в пространстве: онлайн-калькулятор
Расстояние от точки до прямой в пространстве равно длине перпендикуляра, опущенного из точки на прямую. Чтобы быстро узнать ответ задачи, можно использовать автоматические подсчеты. Набор калькуляторов поможет вычислить результат любого задания по алгебре и геометрии.
Сервисом пользуются учащиеся школ и университетов. Также за готовым решением обращаются преподаватели, родители учеников и специалисты инженерного профиля.
1. Выберите, в какой форме представлено уравнение прямой.
2. Введите данные в соответствующие окна. Отправьте задание на вычисление кнопкой «Рассчитать».
3. Получите решение и ответ.
2. Введите данные в соответствующие окна. Отправьте задание на вычисление кнопкой «Рассчитать».
3. Получите решение и ответ.
Видео:7 класс, 38 урок, Расстояние от точки до прямой. Расстояние между параллельными прямымиСкачать

Материалы, которые помогут вам лучше разобраться в теме:
Видео:Расстояние от точки до прямой (метод координат)Скачать

Как найти расстояние от прямой до точки в пространстве. Онлайн-калькулятор
Вычислить расстояние между точкой и прямой в пространстве можно по формуле:
Программа автоматически выполняет комплекс действий. Нет необходимости вычислять результат каждого действия отдельно. Это сокращает время на решение задания и исключает ошибки и потерю данных.
Видео:Лекция 24. Расстояние от точки до прямой на плоскости.Скачать

Почему калькуляторы на нашем сайте часто используют:
- Вы получаете быстрый расчет без ожидания регистрации и перехода по сторонним страницам. Во время проверки знаний особенно важно без промедлений получить решение.
- Расчеты на сайте не требуют платежей. Раздел с вычислениями позволяет ученикам повышать свой уровень знаний без посторонней помощи. Понятный интерфейс с подробными действиями позволяет лучше запомнить материал.
- На запросы не установлены ограничения. Тренироваться в подсчетах, используя любую программу раздела, можно необходимое количество раз в удобное для вас время.
Пошаговые вычисления помогут проверить собственные расчеты, выявить ошибки в алгоритме. Готовое решение можно использовать в качестве примера, запоминать и применять в аналогичных заданиях. Во время зачета или экзамена на сайте можно быстро решить задание и получить хорошую оценку. Если тема не поддается освоению, обратитесь к консультанту. Он найдет для вас преподавателя по выгодной цене.
🔥 Видео
Расстояние от точки до плоскости / Вывод формулыСкачать

Расстояние от точки до плоскости. 11 класс.Скачать
Определение кратчайшей расстоянии от точки до плоскостиСкачать

§15 Расстояние от точки до прямойСкачать

7. Расстояние от точки до плоскости (вывод формулы примеры)Скачать

Видеоурок "Расстояние от точки до прямой"Скачать

Аналитическая геометрия, 1 урок, Векторы в пространствеСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

10 класс, 19 урок, Расстояние от точки до плоскостиСкачать

Расстояние от точки до прямой в пространствеСкачать
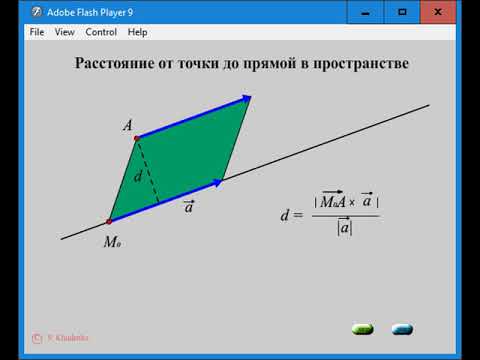
Мировой эфир и отвергнутая наука.Скачать

Расстояние от точки до прямой на плоскостиСкачать

Формула расстояния от точки до прямой (на плоскости)Скачать